基于混合粒子群的无人机对舰船搜索航路优化*

周 波 张尚悦

（1.海军大连舰艇学院基础部 大连 116018）（2.海军大连舰艇学院航海系 大连 116018）

1 引言

随着无人机技术的迅速发展，无人机在海上稽私、海事巡逻、海洋气象监测、船舶遇险后事故救援等领域的应用越来越广。尤其是随着现代物流业的发展，在某些岛屿繁多、交通设施不完善、用邮不便的区域开展无人机航路运营，可兼顾时效性和便利性。

在军事上，无人机以其造价低、体积小、非接触、零伤亡等优势也越来越受到各国的重视。无人机利用其携带的光电、红外传感器、摄像头等多种机载设备，可以在大范围内持续不断地监视海洋或陆地。对于交通流量比较大的港口以及重要的交通要道，无人机在高风险环境下执行任务时，还可根据需要抵近侦察，在较短时间内初步判定目标的类型，一旦发现可疑目标，可及时回传各种信息，为后续的进一步识别、跟踪、搜索、查证做准备。由于无人机执行任务时受多种因素影响，其运动时间有限。因此，执行任务前首先要合理规划飞行路线，获取最优飞行路径［1～3］。

2 无人机搜索问题基本理论

无人机从某个起点出发，对任务海域中各艘舰船进行搜索查证的问题，相当于典型的旅行商问题。需求解无人机飞到各艘目标舰船上空查证并最终返回到起点的最短路径。根据算法实现原理不同，航路优化算法包括图论中的A*算法［4］、Floyd算法［5］、Dijkstra算法等非进化型算法，以及粒子群优化、神经网络算法、禁忌搜索法、遗传算法、模拟退火［6］、蚁群算法等进化算法［1～2］。非进化型算法运算量小、易于实现、处理效率高，但不易产生最优路径；进化型算法通常模拟生物进化特征，能够及时更新、具有一定的记忆能力。

3 PSO算法

3.1 标准粒子群算法

粒子群优化（Particle Swarm Optimization，PSO）模拟鸟类觅食过程中的同伴协作下的运动过程，每个粒子都有一个速度向量，决定其下一步运动的方向和距离。鸟群寻找最优解的过程是通过整个群体的协作和信息共享来实现的，每个解都可以看作搜索空间中的一个多维粒子。根据适应度函数值的变化规律，所有粒子追随当前的最优粒子在解空间中运动［2，7］。

在每一步迭代过程中，PSO粒子的速度受两个因素影响：该粒子目前所找到的局部最优解向量Pbest和整个种群目前找到的全局最优解向量Gbest。标准PSO算法的基本流程如下。

1）粒子群初始化：随机给定每一个多维粒子的初始位置和速度，粒子的维数就是需要搜索的目标数。

2）根据适应度函数公式计算出每个粒子的适应度函数值，从而确定每个粒子的优劣。

3）每一次迭代中，粒子xi(i=1，2，...，n)根据Pbesti和Gbest来更新vi：

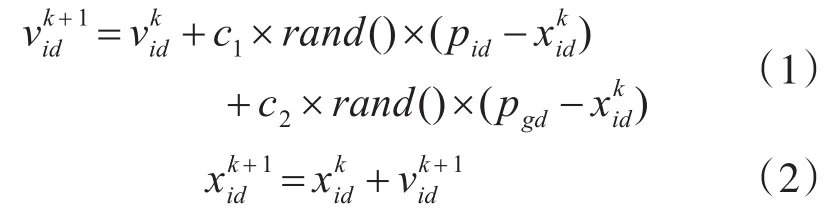
式中，n是粒子总数，为第k次迭代第i个粒子运动速度矢量的第d维分量，为第k次迭代第i个粒子位置矢量的第d维分量，pid为第i个粒子最优位置pbest的第d维分量，pgd为群体最优位置gbest的第d维分量，c1、c2是权重因子［5～6］。

4）为防止粒子陷入局部最优解，引入适当的随机干扰。

5）返回第2）步继续执行，直到找到符合条件的解或者满足终止条件为止。

从1）、2）可以看出，粒子运动的速度和方向受自身最优和群体目前最优两个主要因素影响，在二者共同作用下向最优路径进行动态调整。与其他的进化算法一样，PSO也可能陷入局部极值，出现早熟问题。在式（1）中，如果某个粒子的xid与pid和pgd都十分接近，粒子的速度接近于零，在pgd附近的粒子可能无法跳出局部极值，导致算法收敛早熟［6］。可见，如果粒子的多样性无法满足，整个种群的适应度函数变化受限，无法跳出局部最优继续进行搜索。目前有多种改进PSO方面的研究：比如修改粒子过去飞行速度对当前速度的影响因子，或者引入压缩因子动态调整全局搜索能力和局部搜索的比例关系等。改进目标是增强全局优化能力的同时，加快算法的运行速度，提高收敛时最优解的精度。

3.2 PSO与遗传算法的比较

遗传算法（Genetic Algorithm，GA）模拟生物进化过程在解空间中进行最优搜索。遗传算法三种主要的算子：交叉、变异、选择。交叉和变异可以提高种群多样性，通过选择，适应值高的个体得到更多的复制机会，适应度低的个体在优胜劣汰过程中被淘汰。遗传算法中的需要设定的参数主要有种群大小、染色体长度、交叉概率、变异概率、最大遗传代数等。

PSO和GA都属于生物进化算法，都具有并行性，都是全局优化算法，但PSO算法没有染色体之间的交叉和变异操作，而且PSO与GA的信息共享机制不同。在GA中，所有染色体信息共享，整个种群均匀地向最优解集移动；在PSO中，只把Gbest（Pbest）的信息传递给其他的粒子，信息的传递方向是单方向的，整个种群的更新是密切跟随当前最优解的过程。2000年，Lovbjerg、Rasmussen和Krink提出了混合型PSO，将遗传算法中的交叉概念引入PSO中。从所有粒子中按照一定比例选取待交叉的粒子，然后两个一组，随机组合进行交叉操作产生新的后代粒子。可见，交叉型PSO不但要更新速度和位置，还要进行遗传算法中的交叉操作，用新产生的后代粒子取代其父代粒子。与标准的PSO相比，混合PSO搜索速度快，收敛精度高。在无人机航路优化中，充分利用PSO和GA的各自的特点是一种可行的算法［8］。

3.3 航路规划步骤

1）根据问题的复杂程度，确定种群的大小n（个体数）。

2）确定最大迭代次数、最大迭代次数、粒子移动速度等相关参数。

3）粒子群初始化，每个粒子代表一条初始路径。

4）确定目标函数。

5）计算初始的随机粒子的目标函数。

6）根据式（1）、（2）调整粒子的位置和速度。按照一定的交叉概率Pc，对个体极值和群体极值进行交叉来更新粒子。交叉方式有循环交叉、顺序交叉、位置交叉等［9］。本文采用单点交叉。对于选定的两个 父代个 体g1=x1x2......xn-1xn+2，g2=x'1x'2......x'n-1x'n+2。

随机地选取第m个基因处为交叉点：

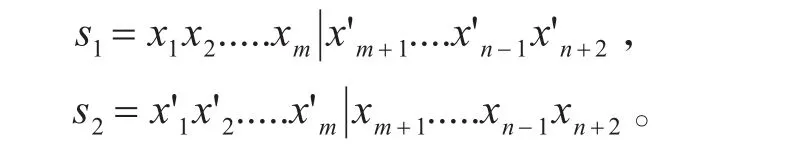
经过交叉运算后得到的新的子代粒子s1和s2。

计算新粒子s1和s2的适应度函数值，若新粒子的适应度函数值的小于历史最优，则对历史最优进行替换，若大于历史最优，则继续保持原来的历史最优。

7）返回步骤5）重新执行，若达到最大迭代次数则退出循环，输出最优路径规划结果［10～12］。

4 仿真实例

假定在某一港口处（坐标为原点）部署无人机起降平台，无人机从此处出发，对横向距离40km，纵向距离80km内的若干舰船目标进行搜索。共进行三次实验，任务区的舰船目标数量分别为20、50、100。无人机运动速度为120km/h。分别用混合粒子群算法和遗传算法求解最优路径。实验所用电脑配置为Windows7 64位系统，4GB内存，程序在MatlabR2015a平台运行。仿真结果如图1～3所示，最优路径长度和算法执行时间如表1所示。

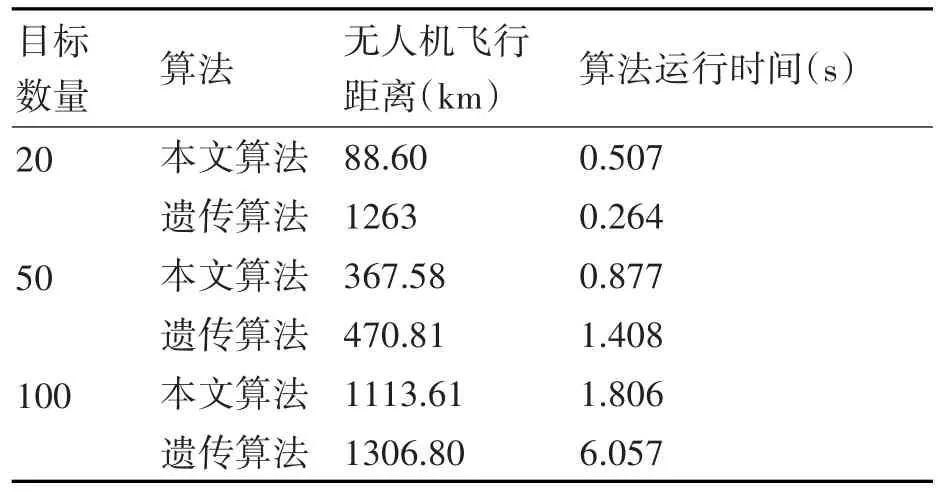
表1 不同算法运行结果比较

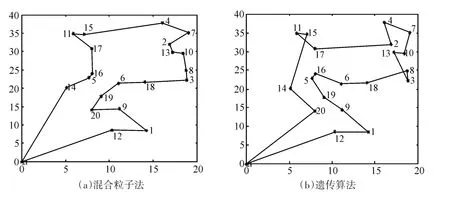
图1 无人机对舰船的搜索路径（20个目标）

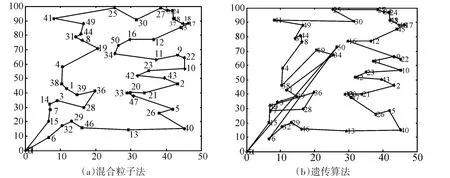
图2 无人机对舰船的搜索路径（50个目标）

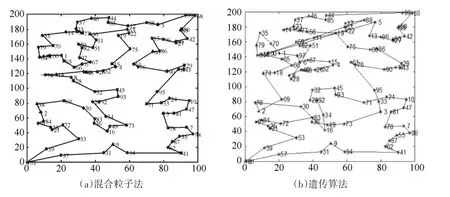
图3 无人机对舰船的搜索路径（100个目标）

从表1可以看出，本文算法求解的最优路径长度明显优于遗传算法，从算法的运行时间看，在目标数量为20的时候，遗传算法速度较快，但是当目标速度上升到50和100时，遗传算法运行速度明显落后于本文算法。混合粒子群算法能够得到满足要求的最优航迹，而且，在种群维度较高的情况下，也能够保证快速完成航路规划。

5 结语

在交通流量较大的港口，利用无人机对进出港舰船进行搜索可以大大提高海上巡查的效率。本文算法还可以用于无人船、无人艇的航路优化。下一步将继续研究无人机集群的航路规划，进一步提升检测效率。