基于自适应支配和参考向量的高维多目标优化算法
2021-06-02孙文静李军华
孙文静, 李军华
(南昌航空大学 信息工程学院,南昌 330063)
引言
多目标优化问题(Multi--objective optimization problems,MOPs)[1]包括2个或3个优化目标。当目标数大于4个时,则升级为高维多目标问题(Many-objective optimization problems,MaOPs)[2-3]。随着目标维数的增加,一般的多目标进化算法(Multi-objective evolutionary algorithms,MOEAs)在处理MaOPs时会出现性能退化,区分解集的能力下降等问题。为此,研究学者们相继提出许多先进和杰出的算法,这些算法可分为3类:基于松弛支配的算法:通过改进Pareto支配或提出新的支配方法来提高选择压力。例如:g支配[4]、S-CDAS[5]、网格支配[6]、RP支配[7]、角度支配[8]和SDR[9]等;基于分解的算法:通过一组参考点将一个MOP分解为多个单目标子问题或易于管理的MOPs,从而降低问题的求解难度。例如:RVEA[10]、AMOEA/D[11]和SPSAT[12]等;基于指标的算法:采用指标作为适应度值来指导种群进化过程,如HypE[13]、MOMBIII[14]等。
尽管大多数MOEAs提高了高维目标空间的搜索能力,但平衡种群收敛性和多样性的能力仍然不足。针对这一问题,本文提出一种基于自适应支配和参考向量的高维多目标优化算法(An adaptive dominance and reference vector based evolutionary algorithm for many-objective optimization, ADRVEA),该算法首先根据种群分布、目标维数等信息构建自适应小生境方法;然后引入分解方法来进一步增强全局目标空间的多样性;最后构建适应度表达式来选择精英个体。
1 相关知识
1.1 背景知识
MOEAs中广泛采用Pareto支配关系,但基于Pareto支配的算法在处理MaOPs时效果较差,这是由于:
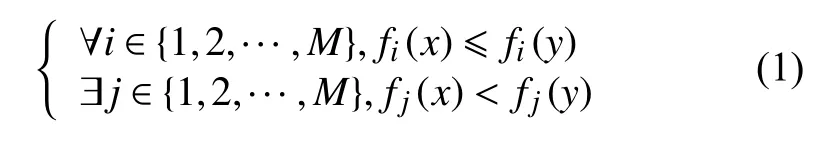
式中:f(x) = (f1(x),f2(x),…,fM(x))是M维目标值,解之间的支配概率为1/2M-1,该概率随M增加而呈指数下降,则产生“支配阻抗”现象。为此,研究者们通过改进支配区域或修改支配关系来解决这一困难。
1.2 改进支配方法
第1类,扩大支配区域的方法:通过扩展解的支配区域来提高选择压力;S-CDAS[5]通过修改解的目标值来自适应控制解的支配区域。第2类,基于网格支配的方法:将目标空间划分为若干个网格,并利用每个解的网格值判断Pareto支配关系;Yang[6]提出以个体为核心的网格计算来确定网格环境中解之间的关系。第3类,引入参考点的支配方法;g支配[4]在最优点的附近估计有效集;Elarbi[7]提出基于参考点和Pareto支配的RP支配。第4类,自适应小生境支配方法:通过自适应小生境达到区分解的目的;SDR[9]根据候选解分布提出了小生境机制,并在每个小生境内确定收敛性最好的解。
1.3 分解方法
RVEA[10]通过一组均匀分布的参考向量来划分目标空间,并建立解与参考向量之间的联系,选择与参考向量最近的候选解,从而引导种群对MOEAs的搜索。SPSAT[12]通过空间分割选择机制来提升多样性,但为了进一步增强收敛性和多样性,采用基于角度的截断机制作为环境选择的第二选择标准。
目前,大多数参考向量生成方法采用Das和Dennis提出的系统方法,该方法通过在M-1维的单位超平面上生成一组均匀分布的参考点。若在每个目标上划分H份,那么M维目标空间中总数为N的参考点为:
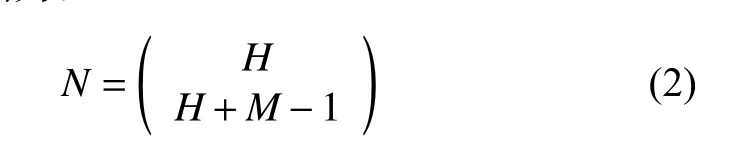
2 基于自适应支配和参考向量的高维多目标优化算法
2.1 ADRVEA的算法框架
为了提高种群收敛性和多样性之间的平衡,本文提出一种基于自适应支配和参考向量的高维多目标优化算法。算法1为ADRVEA框架的伪代码,首先初始化产生N个初始种群和参考向量;然后采用遗传算子生成子代种群;最后将父代种群和子代种群合并,进入环境选择,直到满足终止条件,确定最终的种群。
算法1ADRVEA框架

2.2 ADRVEA环境选择
环境选择的目的是为了从2N个合并种群选择N个收敛性和多样性良好的解集进入下一代。ADRVEA环境选择的伪代码见算法2,首先对合并种群的目标值进行平移;接着对平移后的种群进行一次AD非支配排序,该步骤是为了获得种群中的解所对应的非支配层数,从而构建最终的适应度函数。

1)划分子空间。
为了进一步增强种群的多样性管理,引入参考向量对划分目标空间,并在每个子空间内建立解与参考向量之间的联系,从而获得一组多样性较好的子种群。若一个解和参考向量之间的夹角最小,则该解属于这个参考向量。由于每个子空间内,可能存在多个解与参考向量相属,这些解将组成同一子空间内的子种群。
2)适应度表达式。
为了实现精英选择,对每个子种群构建合理的适应度表达式。根据AD排序的非支配层数和子种群内的角度信息构建适应度函数,具体表述为:
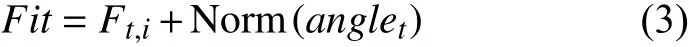
式(3)中:Ft,i为第t代下解i的非支配层数,Norm(anglet)表示归一化后的角度值。ADRVEA中,适应度值越小越好。式(3)在满足2种条件下完成精英选择:①当子种群内解的非支配层数不同时,优先选择非支配层数较小的解;②若满足条件1,进一步选择与参考向量夹角最小的解。
3)自适应支配方法。
AD定义:①当解i与解j在同一小生境内,且i的收敛度小于j;②当解i与解j不在同一小生境内,且i的收敛度远小于j时;满足①和②中任一条件,解j被解i支配(i≺ADj)。解的支配区域由两部分组成:小生境内和小生境外的有限区域。当小生境大小增加时,支配区域随之增加,因此自适应小生境大小可以调整解的支配区域。
根据目标空间中解集的角度信息和目标数来自适应小生境大小。首先计算目标空间中任意解间的最小角度,并组成角度集合;然后对角度集合内的角度进行排序,序号是根据种群大小和目标数确定:
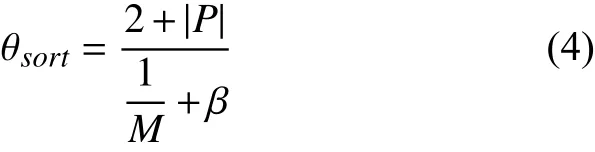
其中M是目标数,|P|是种群大小,β是控制因子。由于进化过程中非支配解比例随M增大而增加,因此考虑M可以自适应地控制解的支配区域。AD通过候选解间的角度和目标数来自适应小生境大小,在一定程度上达到动态控制支配区域的目的。
3 实验研究与结果分析
3.1 实验设置
采用DTLZ[15]和WFG[16]测试集以及GrEA[6]、KnEA[11]、MOMBI-II[14]和RPEA[7]4种算法与ADRVEA进行对比。为了公平对比,算法的种群大小与参考向量大小保相同,具体设置见表1。MOEAs生成子代的遗传算子是模拟的二元交叉[17]和多项式突变[18]。另外,GrEA[6]中网格划分的数div设为5;RPEA[7]中参考点生成的个体比例α设为0.4,参考点和个体之间的差异δ设为0.1。对于任意目标数的测试问题,最大代数设置为1000。

表1 参考向量的数目设置
采用反世代距离加(Modified inverted generational distance, IGD+)[19]和超体积(Hypervolume,HV)[13]指标在每个测试实例上执行30次,并采用0.05显着性水平的Wilcoxon秩和检验来分析结果。
3.2 实验结果分析
3.2.1 DTLZ测试集上的性能对比
表2为GrEA、KnEA、MOMBI-II、RPEA和ADRVEA在DTLZ1-4上IGD+的均值和标准差。由表可见,ADRVEA在处理不同目标的DTLZ1和DTLZ2测试问题时性能良好。由于DTLZ3存在大量局部PF,则该问题可测试MOEAs能否跳出局部PF,ADRVEA在处理5、8、10和15目标时的性能明显优于其他算法。DTLZ4测试PF高度偏向的情况下算法保持候选解分布的能力,ADRVEA在3、5和10目标测试实例中IGD+值突出,说明ADRVEA在该问题下能够保持种群的多样性。
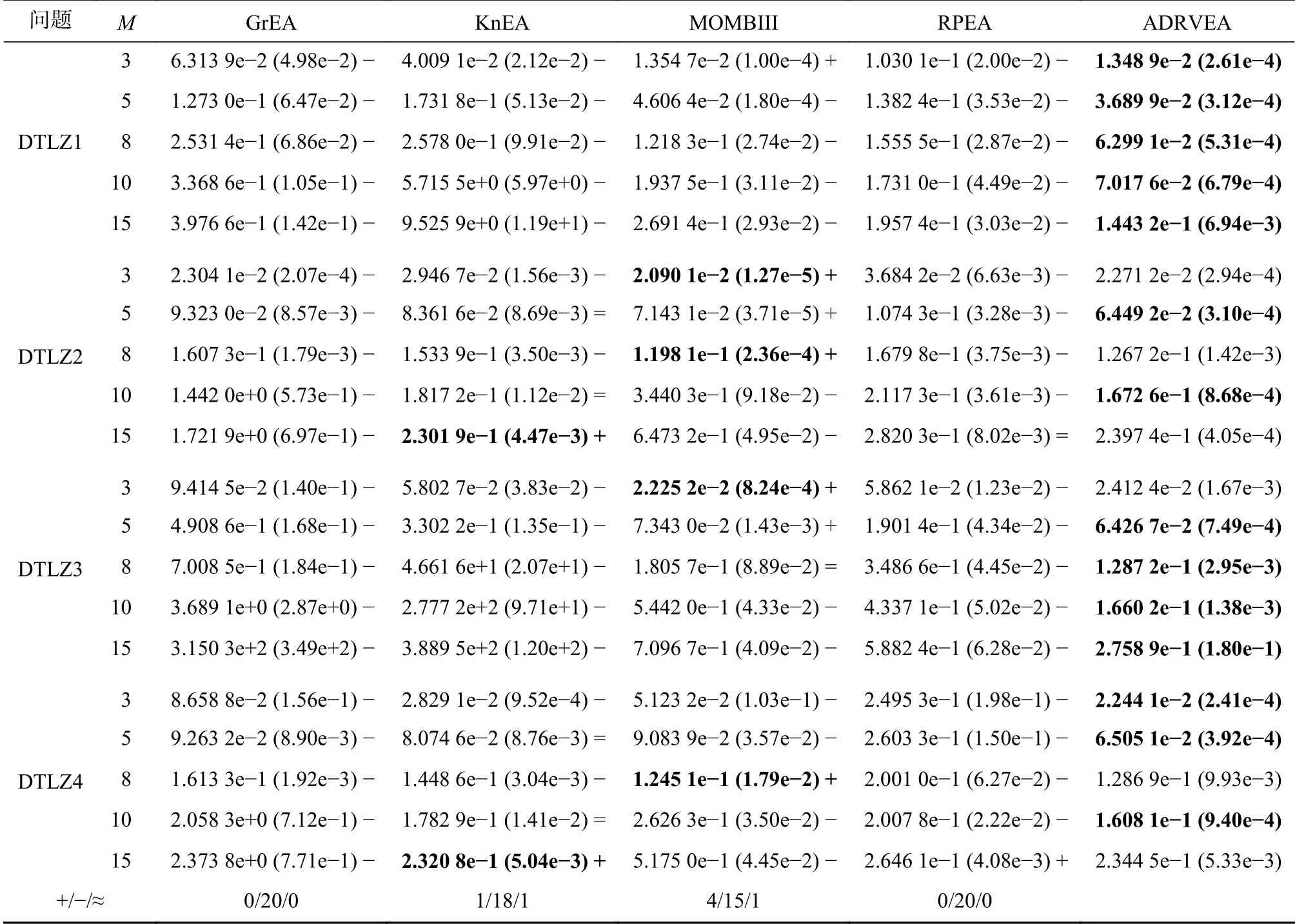
表2 对比算法在DTLZ1-4上获得IGD+的均值和标准差
3.2.2 WFG测试集上的性能对比
表3为不同算法在WFG1-9上获得IGD+值的均值和标准差。可见,ADRVEA和KnEA在混合结构PF的WFG1上性能明显优于其他算法。ADRVEA在处理5、8、10和15目标断开PF的WFG2时算法良好。WFG3具有线性和退化的PF,RPEA在处理该问题时明显优于其他算法。WFG4-9都有凹型的PF,但在决策变量空间的设计存在不同困难。WFG4的PF是多模态,虽然KnEA在处理15目标时性能最佳,但ADRVEA在5、8和10目标时性能突出。WFG5具有欺骗性特征,ADRVEA在5、8、10和15目标中性能显著。在处理具有不可分且缩放PF的WFG6时,ADRVEA总体性能良好。
WFG7的PF具有可分离的单峰,ADRVEA在处理5、8和10目标时取得显著的性能。WFG8具有不可分的特性,ADRVEA和KnEA在该问题上性能总体良好。WFG9具有复杂的特性,则处理WFG9成为难题,但KnEA和ADRVEA具有一定的竞争力。
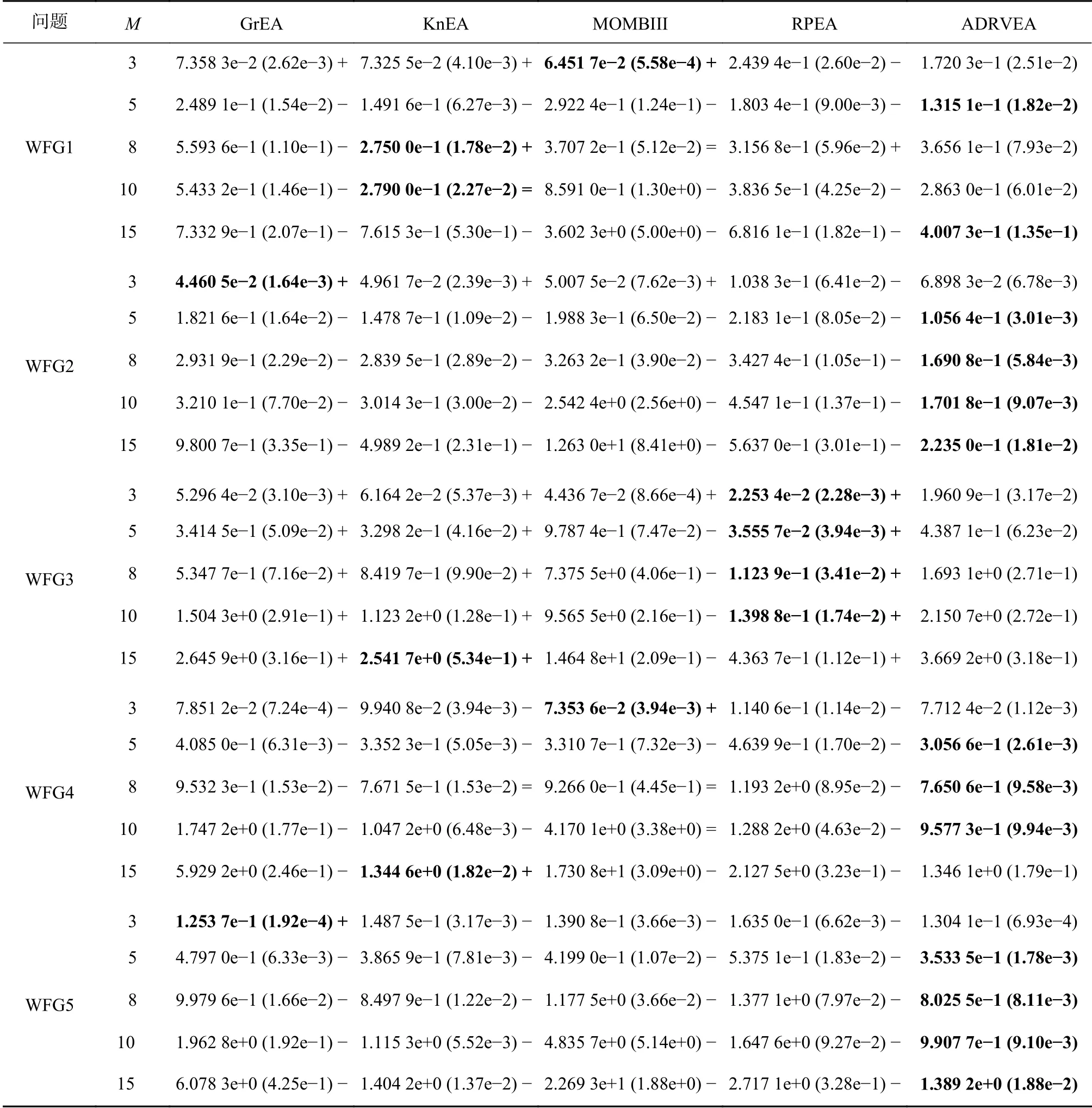
表3 对比算法在WFG1-9上获得IGD+的均值和标准差
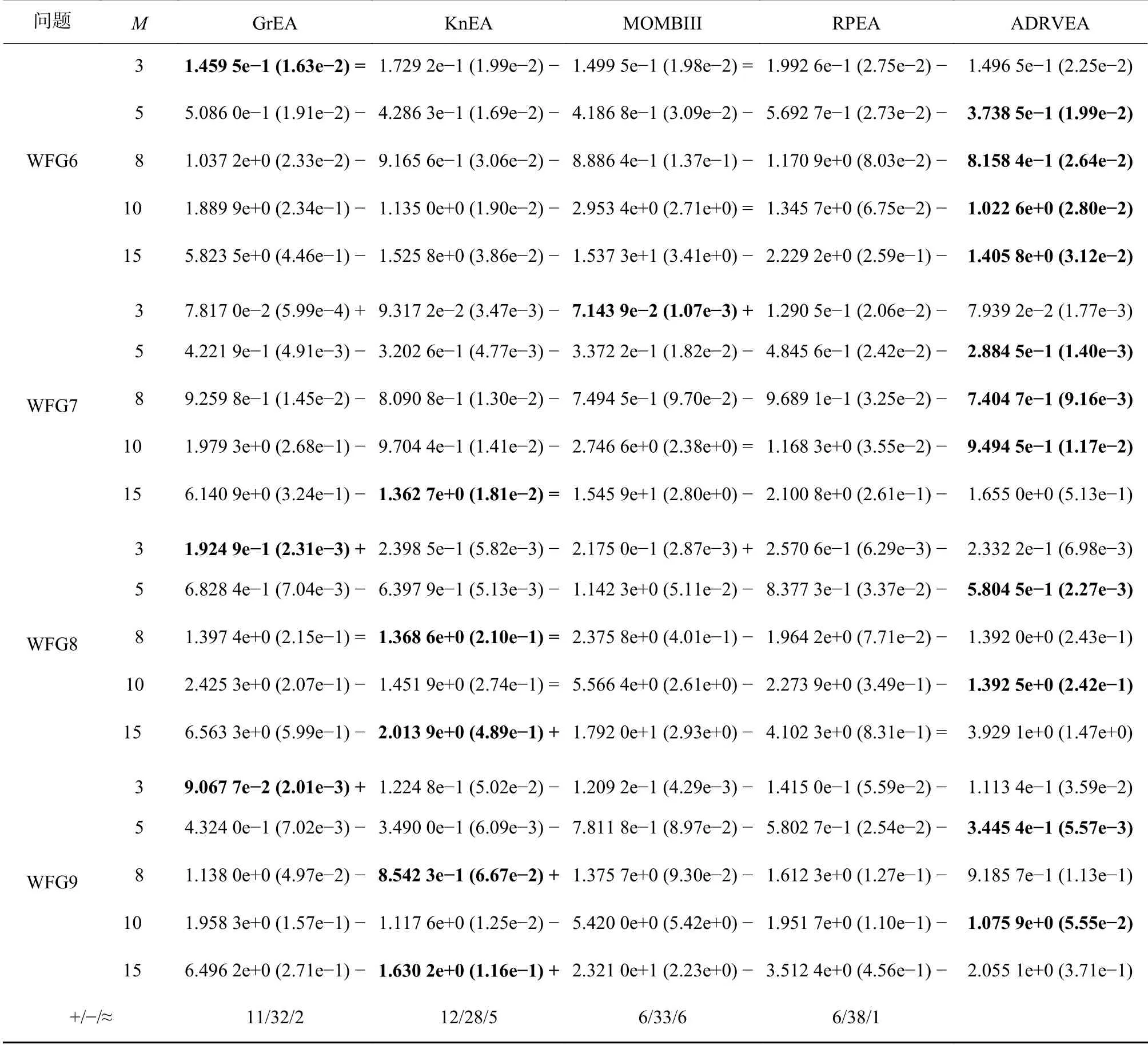
续表3
综合以上分析,ADRVEA在高维目标空间中不仅能获得收敛性和多样性良好的非支配解集,且在不同测试问题中保持优良的算法性能。
3.2.3 AD的对比性分析
将AD与4个支配关系:Pareto支配[20]、g支配[5]、SCDAS[6]和SDR[10]嵌入NSGA-II框架中进行性能比较。基于该5种支配的算法在5、8、10和15目标的DTLZ1-4和WFG1-9测试实例中独立运行30次,获得表4的HV平均值。由表4可见,在总共51个测试实例中,基于AD的算法在30个测试实例中性能显著,且其HV值超过其他支配方法。图1为基于5种支配关系的NSGA-II在10目标WFG8上的非支配解,见图1,Pareto支配关系在高维目标空间中会“失效”;基于g支配的种群在1~10目标上收敛速度很慢,而在10~15目标已收敛至0~1范围,种群陷入局部收敛;基于SCDAS的解集在目标轴上大量缺失解集,覆盖性、收敛性和分布性较差;基于SDR的种群覆盖性较差,在1~2目标上丢失解集,且解集分布性较差;而基于AD的种群在整个目标空间中覆盖性良好,扩展性较好,且有效地收敛到0~1目标值范围,种群分布较为均匀。
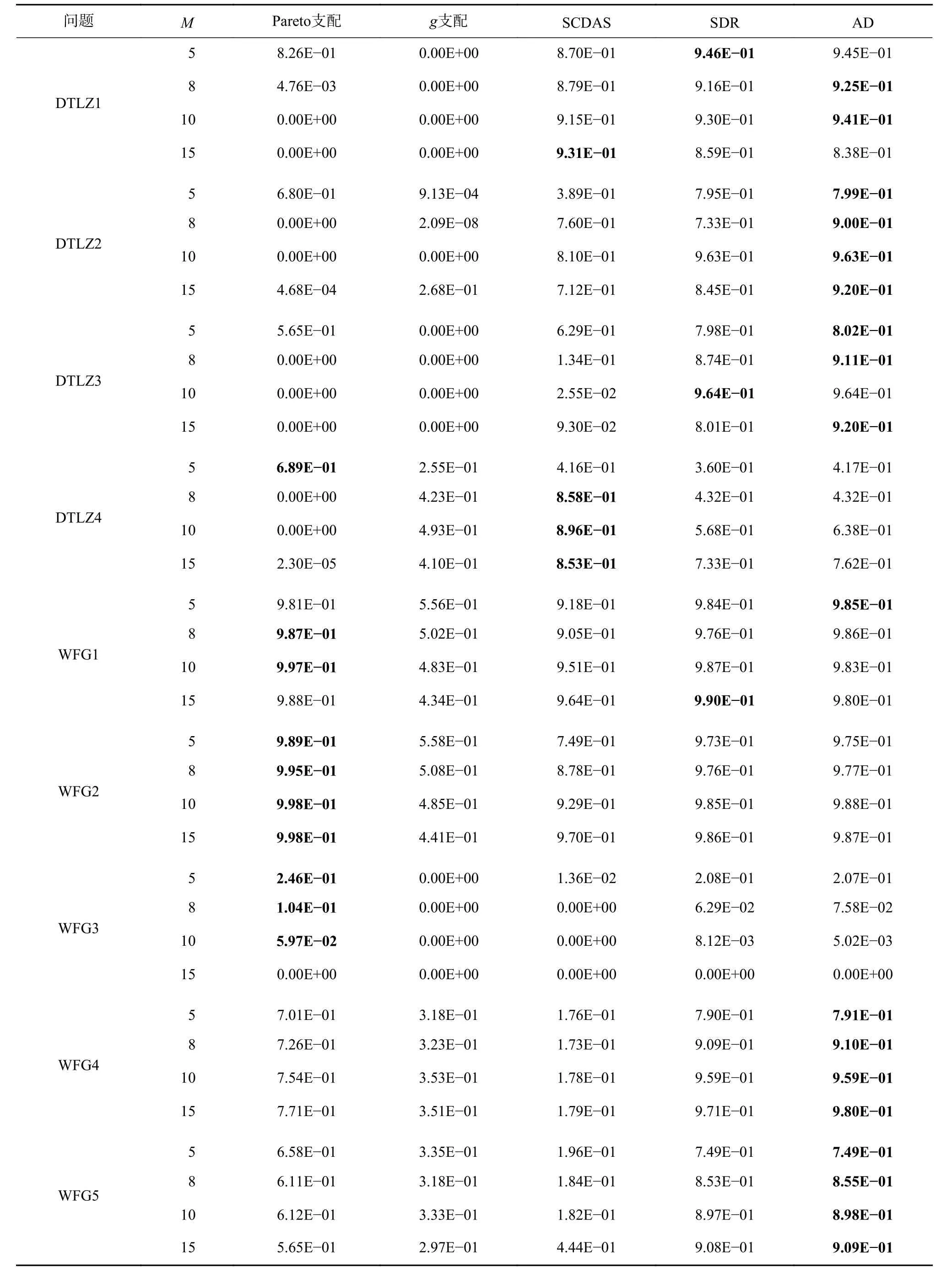
表4 5种支配关系在DTLZ1-4和WFG1-9上的HV平均值
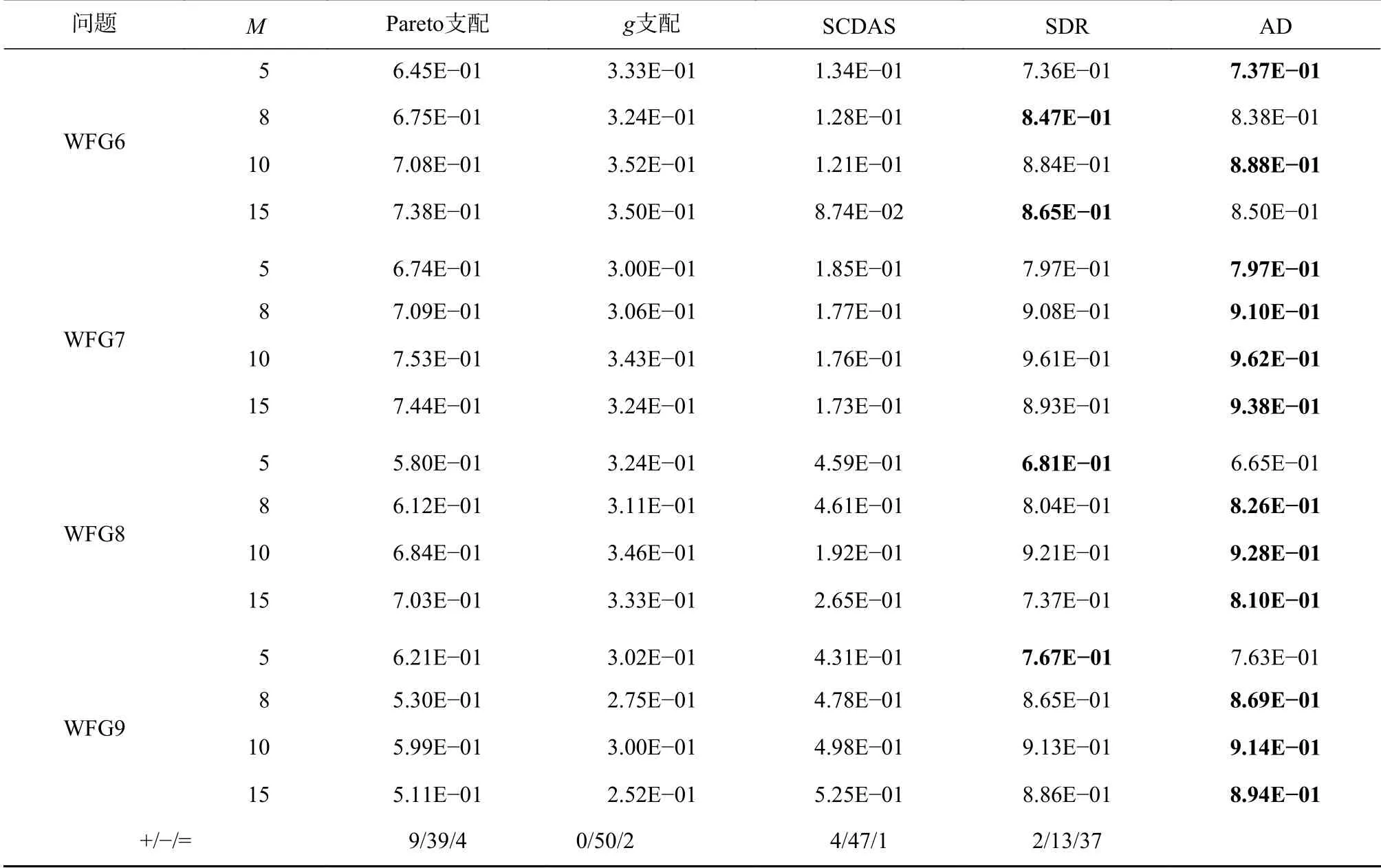
续表4
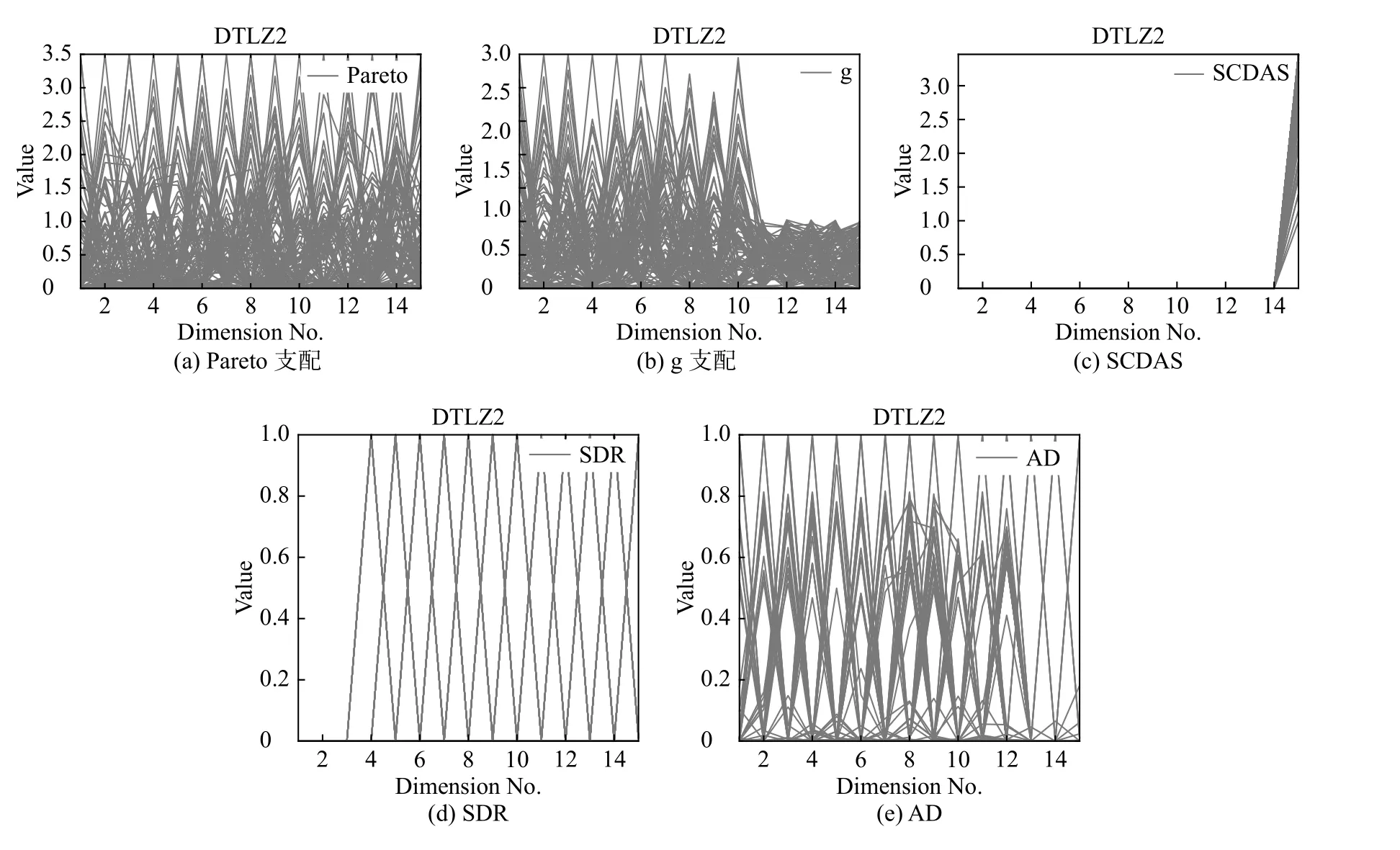
图1 基于5种支配关系的NSGA-II在10目标WFG8上的非支配解
3.2.4 AD的有效性分析
为了验证自适应小生境大小对控制非支配解比例的有效性,在8、10和15目标DTLZ1和DTLZ3上对AD监测30次进化过程中的小生境大小和非支配解比例的平均变化情况。
图2为进化过程中非支配解的比例和小生境大小的变化趋势。由图可见,由于在8、10和15目标下算法的非支配解的比例接近0.5,AD中自适应小生境大小对控制非支配解比例有效。M目标DTLZ1和DTLZ3的PF分别是线性和凹型,由于在高维目标空间中的候选解更加稀疏,固定小生境大小无法动态地适应高维目标空间,因此在进化过程中自适应地调整小生境大小更有助于解决MaOPs。
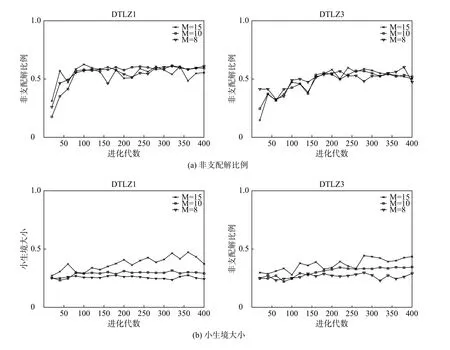
图2 非支配解的比例和小生境大小的变化趋势
3.2.5 控制因子β 的敏感性分析
在AD中,不同的控制因子β取值直接影响小生境大小的变化。选取DTLZ3和WFG2问题,对β进行1~9的数值设置并独立完成30次的优化运行,获得图3的IGD+轨迹变化。
由图3a可见,除了3和5目标DTLZ3,当β值为1~3时,IGD+值随β值的增加而略微减小,此时ADRVEA的算法性能有所提升;而当β值大于3,IGD+值而随β值增加逐渐增大,ADRVEA性能开始骤降;然后,由图3b可知,在任意目标的WFG测试实例中,当β值为1~3时,ADRVEA的IGD+值会随β值增加而相应地减小,算法性能随之增加;而当β值大于3后,ADRVEA性能却开始下降;最后,当β值为3时,ADRVEA在处理任意目标DTLZ3和WFG2时,IGD+值都在0.02~0.27范围内变化,即,当β值为3时,ADRVEA在解决更高维目标的问题时,IGD+值并没有增加,说明ADRVEA能够稳定地维持性能。因此,综合考虑,指定β值为3。
4 总结
针对改进支配方法平衡种群收敛性和多样性不足的问题,提出了一种基于自适应支配和参考向量的高维多目标优化算法(ADRVEA)。研究结果表明:
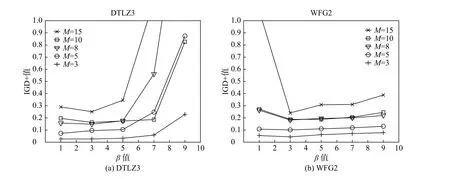
图3 ADRVEA的IGD+轨迹变化
1) ADRVEA不仅总体性能良好,且有效平衡了种群的收敛性和多样性。
2)与现存的支配方法相比,提出的自适应支配具有一定的竞争性。
