基于深度学习的高维稀疏数据组合推荐算法
2020-04-15李晓峰
李晓峰,李 东
(1.黑龙江外国语学院 信息工程系,黑龙江 哈尔滨 150025;2.哈尔滨工业大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
0 引 言
云数据库中存储了大量的高维稀疏数据,对高维稀疏数据的有效组合推荐是保障云数据库得到有效访问和检索的关键。通过对高维稀疏数据特征空间的重构和降维处理,提取高维稀疏数据的关联规则特征量,实现对高维稀疏数据的组合推荐[1],提高对云数据库的访问和自动检索能力。研究高维稀疏数据的推荐模型,对实现高维稀疏数据库的最优分布设计和云组合模型设计具有重要的应用价值,相关的高维稀疏数据组合推荐算法的研究受到了极大关注。
文献[2]提出一种面向稀疏和虚假评分的协同推荐方法。运用低秩矩阵补全理论对稀疏矩阵进行填充,根据填充结果建立群组模型,并构造一个项目评分矩阵,借助协同过滤算法对稀疏数据和虚假评分进行协同推荐。根据实验结果可知,该方法能够有效应对虚假评分,推荐结果较优,但在数据推荐过程中,并未对数据进行自适应寻优,直接采用协同过滤算法完成数据推荐,导致时间开销较大。文献[3]提出基于联合聚类与用户特征提取的协同过滤推荐算法,根据联合聚类识别方法对用户偏好进行有效识别,根据识别结果提取公共特征,采用相似度概念对公共特征进行进一步分析,得出稀疏数据的推荐方法。根据实验结果可知,该算法能够对稀疏数据进行实时推荐,但是仅对高维稀疏数据的公共特征进行分析,并未深入研究数据的平均互信息特征量,导致受到高维特征扰动的影响,使数据存在一定的误差。针对传统算法对高维稀疏数据进行推荐时,存在计算开销大以及推荐的模糊性大等问题,提出一种基于深度学习的高维稀疏数据组合推荐算法。仿真实验结果表明,该算法在提高高维稀疏数据组合推荐能力方面具有优越性。
1 高维稀疏数据分布式体系结构及相空间重构
1.1 高维稀疏数据分布式体系结构
为了实现对高维稀疏数据组合推荐算法的优化设计,结合高维稀疏数据存储节点的分布式结构重组方法,将高维稀疏数据体系建立在基于Web移动社会网络(web-based MSNs,WMSNs)和分散式移动社会网络(decentralized MSNs,DMSNs)的基础上[4],结合向量量化分析方法,构建高维稀疏数据存储节点最优分布模型。用一个二元有向图G=(V,E)表示高维稀疏数据的图模型结构,其中V是部署在数据图模型分布节点的顶点集,E是高维稀疏数据在有限域分布区域G中所有边的集合。假设M1,M2,…,MN为高维稀疏数据的Sink节点,采用欧氏距离表示高维稀疏数据传输节点的相轨迹间距,在高维稀疏数据社区节点的初始链路分布模型下,得到稀疏数据的分布式拓扑结构模型,如图1所示。
结合图1所示的拓扑结构模型,构建高维稀疏数据的有限覆盖区域模型,在高维稀疏数据存储结构网络中,组合推荐模型有向图向量的加权系数为W={u,w1,w2,…,wk},在高维稀疏数据的信息覆盖区域,假设M个高维稀疏数据的网络节点传输链路层数据为x(k-1),x(k-2),…,x(k-M),谐波特征分布节点初始位置xs=[x(η1),x(η2),…,x(ηN)]T的估计值为:
(1)

图1 高维稀疏数据的分布式拓扑结构模型
基于业务优先级划分方法,得到高维稀疏数据传输节点负载模型为:
(2)
(3)
另外,ω(t)为虚拟节点的数据维数,ph(t)为高维稀疏数据Source与Sink节点之间的距离。采用相空间重构方法进行高维稀疏数据的特征重构,结合非线性统计序列分析方法进行高维稀疏数据的回归分析和点云结构重组[5-6],高维稀疏数据相空间重构的结构模型为:
X=[s1,s2,…,sK]=
(4)
其中,K=N-(m-1)τ,表示高维稀疏数据搜索特征空间的嵌入维数,τ为时延,m为虚拟节点和虚拟链路层数,si=(xi,xi+τ,…,xi+(m-1)τ)T称为时隙集合。
根据上述内容可知,运用相空间重构方法对高维稀疏数据特征进行重构之后,再在重构的相空间中进行数据特征提取,有助于提高数据的组合推荐能力。
1.2 高维稀疏数据的组合特征量提取
根据特征量提取结果,对高维稀疏数据的组合特征量进行提取。假设待组合推荐的高维稀疏数据信息流的统计分布序列为{x1,x2,…,xN},令x(n)为一组回归分析的特征量,在m维重构相空间中进行高维稀疏数据的稀疏散乱点云映射,得到高维稀疏数据的分布式重组结构式为:
X(n)={x(n),x(n+τ),…,x(n+(m-1)τ)},
n=1,2,…,N
(5)
其中,τ表示高维稀疏数据在高维相空间中的嵌入延迟。建立状态转移模型,高维稀疏数据的特征评价概念集表达式为:
(6)
挖掘高维稀疏数据的推荐属性的关联规则特征量:
(7)
采用云稀疏散乱点结构重组方法,得到第i个高维稀疏数据的散乱点集为Pi=(pi1,pi2,…,piD)。
采用演进型时隙分配机制[7-8],得到高维稀疏数据的属性混合推荐值计算迭代式为:
(8)
其中,xi(k)表示xi的范数。
采用深度学习算法对组合特征量进行优化提取,计算密集场景中高维稀疏数据在起始时刻T0的统计特征量,得到高维稀疏数据中的演进型时隙分配的信任值为:
(9)
根据信任度进行组合特征推荐时,在超帧结构中得到频谱Z服从参数为βd的高斯分布[9-10],其中:
βd=(MPDist-d+1)/MPDist,d∈[2,MPDist]
(10)
其中,M表示路径的个数,具体为用户端负责处理数据的路径数;βd∈(0,1],采用模糊指向性聚类方法,进行高维稀疏数据的组合特征挖掘和提取,根据特征提取结果实现数据的组合推荐算法设计。
2 推荐算法的优化设计
2.1 高维稀疏数据的主成分分析
在上述采用相空间重构方法进行高维稀疏数据的特征重构和特征提取的基础上,结合非线性统计序列分析方法进行高维稀疏数据的回归分析和点云结构重组[11-12],得到高维稀疏数据的信任关系为A→B,B→C,推出回归分析模型为:
MSDa→b=
(11)
采用特征提取技术抽取高维稀疏数据的平均互信息特征量,输出高维稀疏数据的属性分布的互信息为:
I(Q,S)=H(Q)-H(Q|S)
(12)
其中
(13)
用特征提取技术抽取高维稀疏数据的平均互信息特征量,结合关联规则挖掘方法进行高维稀疏数据的主成分分析,根据高维稀疏数据的属性挖掘结果进行组合推荐,得到数据组合推荐的判决准则满足:
准则(1):
(14)
准则(2):
(15)
根据高维稀疏数据的推荐的判决准则,进行高维稀疏数据的主成分分析。在数据的特征分布属性集中,设{u1,u2,…,uN}表示包含的元素节点集合的高维稀疏数据的类空间分布集合,{v1,v2,…,vM}表示不可信节点集合,R=[Ru,v]N×M表示高维稀疏数据的用户行为集,通过载波监听多路访问控制方法,进行数据的主成分分析,递推公式如下:
(16)
用CIntrai(n)表示高维稀疏数据方位节点i定位的最优间隔,CInteri(n)表示竞争节点i的总时隙。根据上述分析,结合关联规则挖掘方法进行高维稀疏数据的主成分分析,挖掘高维稀疏数据的相似度属性类别成分[13-14]。
2.2 组合推荐输出
采用自适应信息融合方法进行高维稀疏数据输出特征的信息融合,在高维相空间中进行高维稀疏数据的模糊聚类和特征挖掘处理。假设高维稀疏数据的统计特征序列{Xn},n=1,2,…,N,表示原始待推荐的高维稀疏数据特征分布集,在模糊网格区域聚类环境下,得到组合推荐的高维稀疏数据的特征分布为XN=Xn+η,其中η为观测数据的统计特征量。在d个高维稀疏数据的分布空间中,采用相空间重构技术对高维稀疏数据进行特征重构[15],得到当前可分配最大时隙分布:
Xn={Xn,Xn-τ,Xn-2τ,…,Xn-(d-1)τ}
(17)
令Rd×L是d×L的矩阵,设立优先级,通过频繁项挖掘,得到组合推荐输出的高维稀疏数据的平均互信息特征量,为:
R1={X1,X2,…,Xd}T
(18)
配置不同长度的时隙帧,采用深度学习方法进行高维稀疏数据组合推荐过程中的自适应寻优,高维稀疏数据的关联规则向量集为:
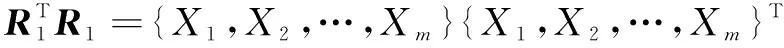
(19)
依据深度学习方法,得到高维稀疏数据的学习过程迭代式为:
(20)
在L+1到2L维的网格区域中,对高维稀疏数据进行降维处理,根据上述方法类推,得到高维稀疏数据组合推荐的输出特征值为:
(21)
R2={Xd+1,Xd+2,…,Xd+m}T
(22)
(23)
其中,高维稀疏数据的测试集V=[V1,V2,…,Vm]∈Rm×m是正交的,即VVT=IM,Σ=diag(σ1,σ2,…,σm)∈Rm×m。采用特征提取技术抽取高维稀疏数据的平均互信息特征量[16],采用深度学习机器算法进行推荐的过程反馈实现误差修正,使得推荐输出的特征向量集RTR满足类间平衡性,综上分析,实现了高维稀疏数据的组合推荐,实现流程如图2所示。

图2 算法的实现流程
综上所述,完成了对基于深度学习的高维稀疏数据组合推荐算法的设计,通过该算法实现了对高维稀疏数据的属性归类与有效识辨。
3 仿真实验与结果分析
为了验证该算法在实现高维稀疏数据组合推荐中的应用性能,结合Matlab和C++编程软件进行仿真实验分析。高维稀疏数据的采样样本数据库来自于云组合数据库Pearson Database,其中Pearson线性相关系数设定为0.34,Spearman秩相关系数设定为0.21,利用K-S检验对推荐过程中的收敛性进行判断,数据的维数设定为40,采样样本的长度设定为1 200,测试集大小为3 000,最优分布类型参数为24.2。根据上述仿真环境和参数设定,进行高维稀疏数据组合推荐仿真分析,依据1.1中给出的高维稀疏数据的分布式拓扑结构模型,构建高维稀疏数据的样本分布时域图,如图3所示。
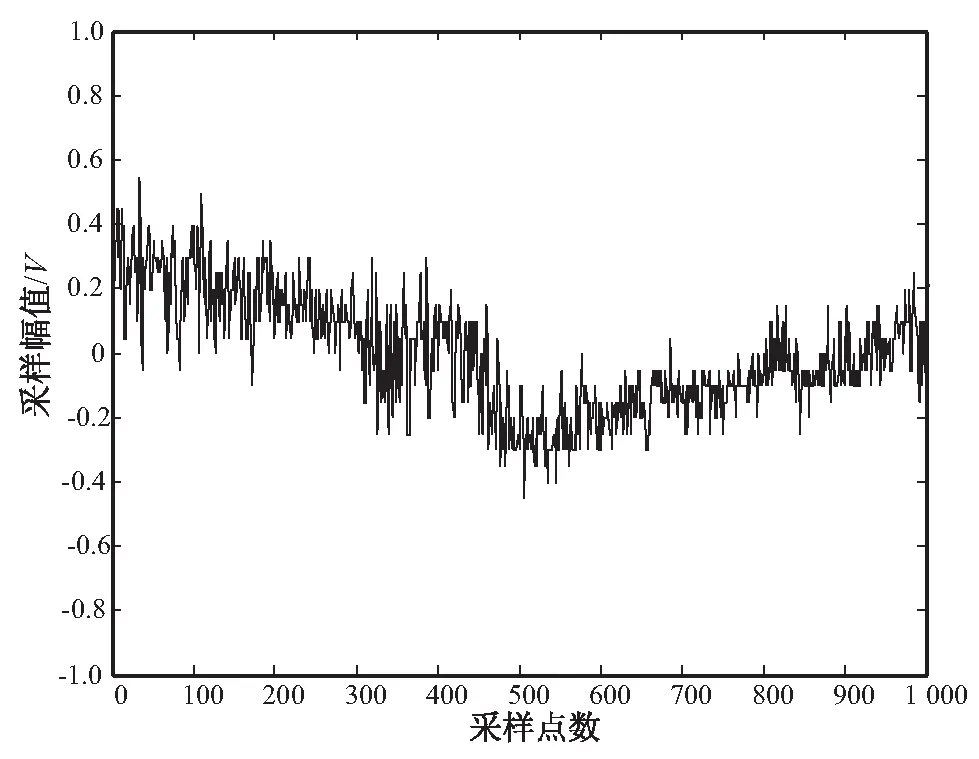
图3 高维稀疏数据的样本分布
根据图3可以看出,构建的高维稀疏数据样本分布均匀,随着采样点数的增加,采样幅值变化较为平稳,表明高维稀疏数据样本质量较好。
以上述数据为研究样本,采用相空间重构方法进行高维稀疏数据的特征重构,提取高维稀疏数据的组合特征量。依据提取得到的高维稀疏数据的组合特征量,实现数据的组合推荐,得到高维数据的推荐输出,如图4所示。

图4 高维稀疏数据的组合推荐输出
分析图4得知,采用该算法能有效实现对高维稀疏数据的组合推荐,对数据的降维表达能力较高,相对于图3,在高维相空间中,对数据的辨识度更明显,推荐能力较强。在特征量提取过程中,主要根据信任度进行组合特征推荐,假设将信任值的分值划分为2-16分,依据式9分别计算文中算法与文献[2-3]算法的信任值,结果如图5所示。
根据图5可以看出,文献[2-3]算法的信任值波动较大,在200-300数据量时,呈现短暂的上升趋势,随后信任值则持续较低,不能很好地完成数据组合推荐。而文中算法在任意高维稀疏数据量条件下,信任值均显著高于文献[2-3]算法,整体信任值在10以上,且波动幅度较小,具有一定的稳定性。
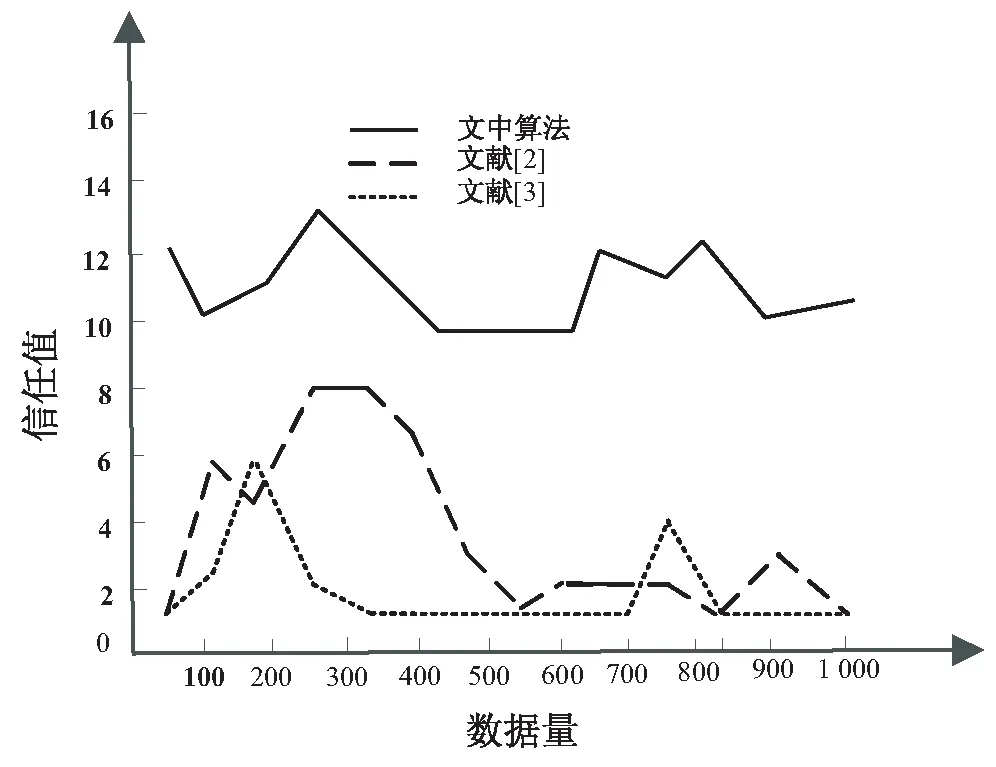
图5 信任值对比分析
对文中算法与文献[2-3]算法进行高维稀疏数据推荐的时间开销和精度对比,结果见表1和表2。
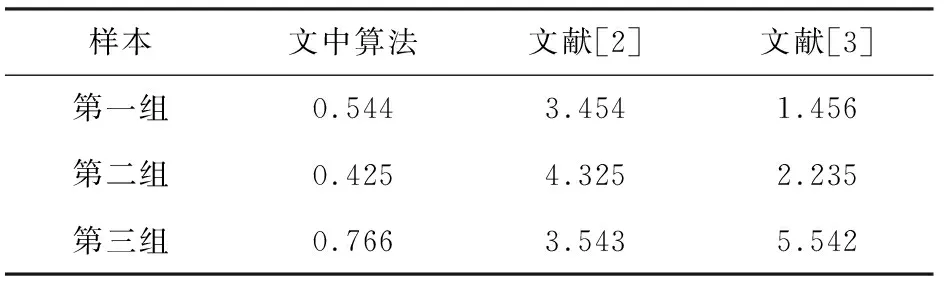
表1 高维稀疏数据组合推荐的时间开销性能对比 s

表2 组合推荐精度性能对比 %
分析表1数据可知,运用文中算法进行高维稀疏数据推荐时,文中算法的最高时间开销不超过0.766 s,远低于文献[2-3]算法。这是因为文中采用深度学习方法进行高维稀疏数据组合推荐过程中的自适应寻优,大大降低了数据推荐耗时。分析表2数据可知,三种算法的推荐精度都比较高,但文中算法的推荐精度均可高达99%左右,显著优于其他两种算法。这是因为文中算法提取了高维稀疏数据特征量,依据特征量提取结果采用特征提取技术抽取高维稀疏数据的平均互信息特征量,在此基础上进行数据推荐分析,降低了高维特征扰动影响,提高了推荐精度。
综合上述分析可知,该算法具有实际应用性,可以为相关领域提供参考价值。
4 结束语
对高维稀疏数据的有效组合推荐是保障云数据库得到有效访问和检索的关键,文中提出基于深度学习的高维稀疏数据组合推荐算法。实验结果表明,用该算法进行高维稀疏数据组合推荐的辨识度较高,精度较好,时间开销较短。未来将继续致力于高维稀疏数据组合推荐算法的研究,会将重点放在分级推荐方面,以期实现个性化、有针对性的推荐效果。
