基于随机维纳过程的结构损伤寿命预测与可靠性评估方法
2021-06-02陈志军李海波胡彦平
陈志军, 李海波, 胡彦平
(北京强度环境研究所,北京 100076)
引言
国内外大量学者对寿命预测方法进行了深入研究[1]。文献[2]将现有的寿命预测方法分为两大类:一是基于失效物理的方法。将产品的机械动力学与实时监测数据综合应用到产品寿命预测上,充分利用了产品的物理效应,使其在没有同类产品历史数据的情况下也可以进行寿命的准确估计,但大多数产品失效机理不明、失效模式难以确定,建立其失效物理模型存在一定的难度。二是基于数据驱动的方法,即不需要建立产品的物理失效模型,主要是依靠产品自身监测数据或者同型产品的历史数据进行产品寿命估计。文献[3]将基于数据驱动的寿命预测方法进一步划分为基于状态外推的方法和基于人工智能的方法。文献[4]从监测数据方面,将寿命预测分为基于直接监测数据的方法和基于间接监测数据的方法。直接监测数据是指试验过程中直接测得的退化数据,间接监测数据是指不能直接反映设备退化状态的数据。现有文献对于间接监测数据的利用还不充分,相关预测方法研究所见不多。
从直接监测数据的角度分析两类工程中最常用的方法的优点与缺陷:
1)基于退化轨迹模型的寿命预测方法:工程上一般采用经典的回归模型来刻画产品性能参数随时间变化的过程,并引入随机系数来表示退化过程中的随机误差。Lu等[5]研究了基于随机系数的性能参数退化回归模型,其后许多专家学者对其研究成果进行了研究推广[6-7]。该类模型认为反映产品总体特征的退化轨迹模型保持不变,变化的只是模型中的参数,而产品个体之间退化差异则通过随机项得以体现。在给定失效阈值后,随机系数回归模型是一种经典的能够实现产品寿命计算的退化轨迹模型。随机系数回归模型是用来刻画产品的退化轨迹模型,而对应的寿命则是用来刻画产品退化量达到给定失效阈值的时间。该类模型认为随机项和确定项是相互独立的,模型中参数一般采用两步法来进行估计[8-9]。考虑到该模型描述的是总体寿命特征,而不能描述个体之间的性能变化差异。对于产品个体来说,模型系数为一常数,即退化轨迹为一条确定的曲线。因此该模型依据状态监测数据估计得到的寿命仅能代表产品共性特点,难以凸显产品个性特征,有一定的应用局限。
2)基于维纳过程的剩余寿命预测方法:在工程实际中,由于产品本身处在一个内、外应力变化不一且各时段所承受的工作载荷不同的环境中,导致产品的性能退化并不具备单调特性。通过研究发现,维纳过程可以同时刻画产品的单调与非单调退化,并在工程上得到了广泛应用[4]。
Si等[10-11]提出了一种基于维纳过程的产品寿命预测方法,给出了产品寿命的概率密度函数表达式,得到了产品剩余寿命的矩估计。考虑到工程实际中多数产品的退化并不都满足线性特征,Si等[12-13]进一步提出了一种基于非线性维纳过程的产品寿命预测模型,给出了产品寿命的概率密度函数表达式,得到了产品剩余寿命的矩估。
本研究在诸多学者研究的基础上,提出一种基于随机维纳过程的结构损伤寿命预测与可靠性评估方法。一方面基于性能退化数据,引入无偏估计结合最小二乘原理进行模型参数估计,建立寿命预测模型和可靠性评估模型,进而完成寿命预测和可靠性评估;另一方面,通过实例对比分析基于随机维纳过程的建模方法与基于退化轨迹模型的建模方法的适用性和有效性。
1 基于随机维纳过程的寿命建模
1.1 基于随机维纳过程的性能退化模型
产品的性能退化过程实际上是一个随机过程,退化模型种类较多,有常见的线性模型、幂模型和指数模型,但是此3种模型的适应性较窄,因此,选取模型适应性较广的随机维纳过程来分析性能参数的退化行为,基于随机维纳过程的性能退化模型如下:

其中:X(t)为性能退化量;µ为漂移系数且µ>0;σ为扩散系数;∆X(∆t)为标准布朗运动且∆X(∆t)。
根据维纳过程的特性,性能退化增量∆X(∆t)满足:
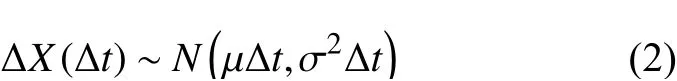
对于计算得到的性能退化增量值,可以采用Anderson-Darling拟合优度检验方法确定最优分布是否为正态分布。
Anderson-Darling拟合优度检验方法具有良好的统计特性,一般选用此方法来确定分布类型。Anderson-Darling统计量可描述数据服从特定分布类型的程度,数据与分布拟合的越好,Anderson-Darling统计量的AD值越小,且AD的计算公式如下:
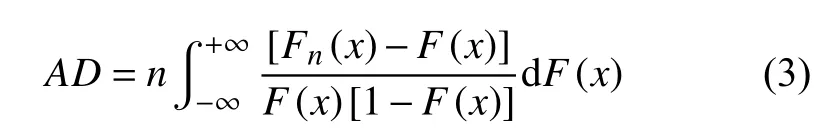
式中:Fn(x)为经验分布函数,F(x)为累积分布函数。
利用Anderson-Darling对最优拟合的分布类型进行假设检验:
H0: 参数值服从指定分布类型;
H1: 参数值不服从指定分布类型
假设选定假设检验的显著性水平为0.05,如果Anderson-Darling的p值大于0.05,则可以得出参数值服从指定分布类型的结论。
1.2 寿命预测模型
设样品的失效阈值l为一常量,当样品退化量X(t)首次达到失效阈值时定义为样品失效,样品寿命T满足式(4)

又得知T服从逆高斯分布,T的可靠度函数和概率密度函数分别为

根据产品寿命值的数学期望,可以推导出其平均剩余寿命的表达式为
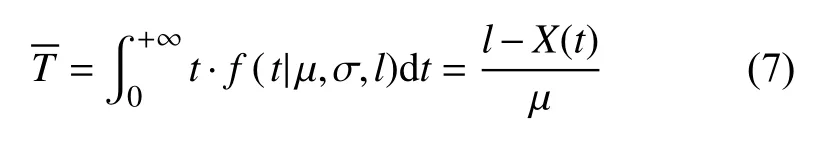
2 模型参数估计
假设试验中试验样本量为n,共进行m次测量,测试时刻分别为t1,t2,…,tm,设第i个样品第j次测试时性能参数值为则可得tj时刻,变量的期望与方差分别为:

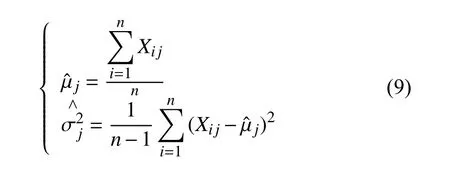
利用式(4)结合最小二乘原理得到µ和σ2得估计值为
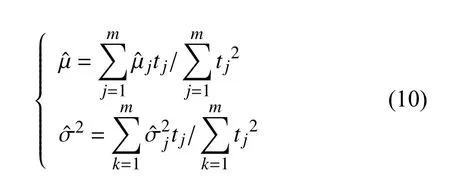
3 寿命预测

则可计算得到参试的n个样本的寿命估计值为:
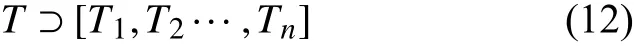
4 案例分析
以某齿轮为例,其主要失效是裂纹扩展损伤达到极限值即可判定该齿轮失效,案例采用恒定应力退化试验方法对该齿轮进行性能退化研究。
1)选取21个样本分3组(每组7个样本)开展3批试验,试验中每10 000个循环(一个循环为齿轮转一圈)进行一次测量,记录裂纹长度,试验共进行12万个循环,有12个样本故障,试验数据见图1。

图1 裂纹长度随时间变化趋势图
2)该齿轮裂纹失效阈值为1.6英寸。
图中样本C001在循环次数为90 000次时检测出故障,样本C002在循环次数为100 000次时检测出故障,样本C003、C004、C005、C006、C007、C008在循环次数为110 000次时检测出故障,样本C009~C012在循环次数为110 000次时检测出故障。
4.1 性能退化数据增量分布检验
将试验获取的21个样本的性能退化增量进行正态分布检验,分析结果如图2~图8所示。
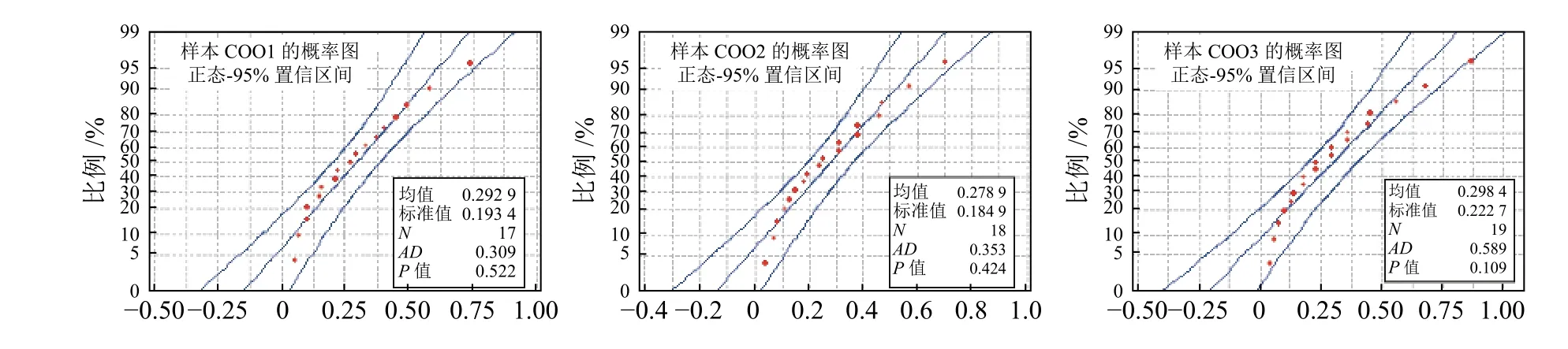
图2 样本C001~C003性能退化增量概率图

图3 样本C004~C006性能退化增量概率图

图4 样本C007~C009性能退化增量概率图

图5 样本C010~C012性能退化增量概率图
通过正态概率图可以得出:各样本的退化数据增量均服从正态分布,因此可以用weiner过程来描述试验样本的性能退化过程。
4.2 模型参数估计
利用式(9)可得第j次测量时,µj和的无偏估计见表1。
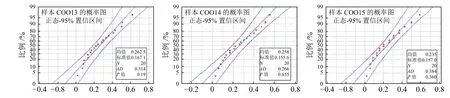
图6 样本C013~C015性能退化增量概率图

图7 样本C016~C018性能退化增量概率图
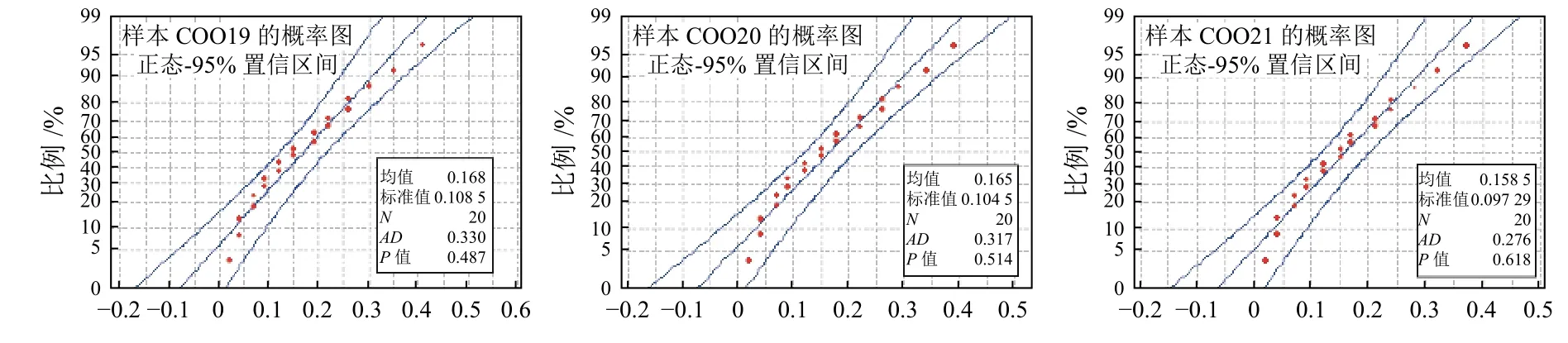
图8 样本C019~C021性能退化增量概率图
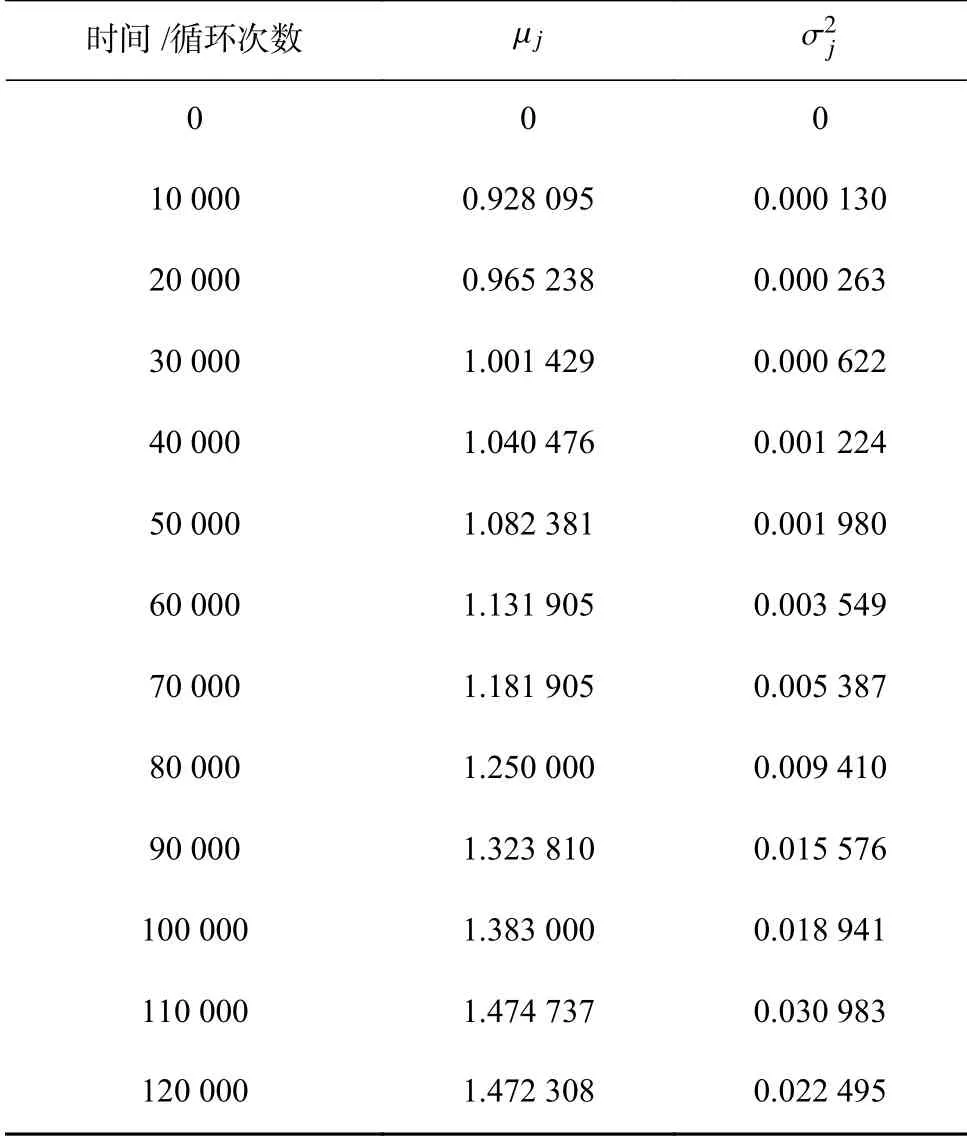
表1 齿轮恒定应力下裂纹扩展稳定性统计特性
利用式(10)结合最小二乘原理得到 µ和σ2得估计值为

则该齿轮性能退化过程可描述如下:

4.3 寿命预测
1)退化轨迹建模计算得到的结果。
通过退化轨迹模型直接拟合计算得到的结果如表2所示。
结合图1、表2计算结果可以得出:1)基于指数拟合的退化轨迹模型与试验数据的相关性很高,可以用于该齿轮的寿命预测;2)通过图1可以明显看出样本2的寿命恰好等于故障检测时刻,而其他11个样本的寿命则明显小于故障检测时刻,通过表1可以看出基于退化轨迹模型预测得出的多数样本的寿命预测值大于故障检测时刻,说明基于退化轨迹模型的寿命预测值有偏大趋势,存在高估寿命的可能。

表2 基于退化轨迹模型直接拟合计算得到的结果
2)随机维纳过程建模计算得到的结果。
根据式(11)及上述寿命模型参数估计值,计算得到21个样本的寿命估计值如表3所示。
结合图1、表3计算结果:1)仅考虑前12个样本,可以得出基于随机维纳过程预测得出的样本的寿命预测值均小于故障检测时刻,且对照图1退化趋势,预测值基本与样本寿命正值吻合,几乎准确预测产品寿命;2)对比2种方法预测结果,可以得出基于随机维纳过程预测得出的样本的寿命预测值相对保守且更接近寿命正值。
4.4 可靠性评估
将计算得到的 µ和σ2的估计值和代入式(5),绘制出该齿轮的可靠度曲线如图9所示。
通过图9可以得到:1)在齿轮运转约92 000循环之前,基于退化轨迹模型的可靠性评估结果和基于随机维纳过程的可靠性评估结果基本一致,这与实际试验获取的退化数据和寿命数据吻合,都能很好地描述其寿命与可靠性;2)当齿轮运转超过92 000循环之后,基于两种模型的可靠性评估结果出现较大差异,结合实际试验获得的寿命数据分析,基于退化轨迹模型的可靠性评估结果存在高估寿命后期的可靠性,基于随机维纳过程的可靠性评估结果可以更准确的预测寿命后期的可靠性。
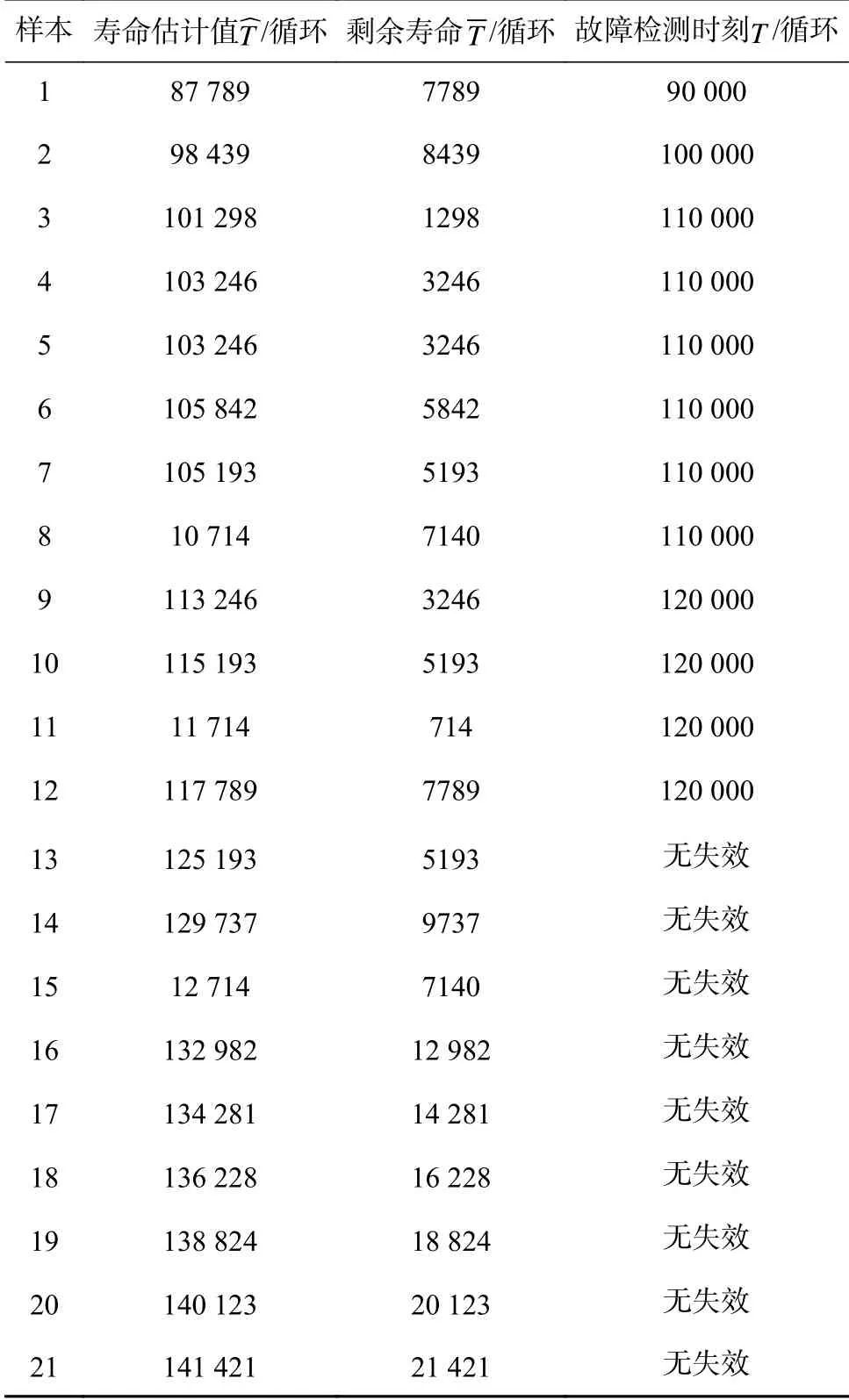
表3 基于随机维纳过程计算得到的结果

图9 该齿轮的可靠度曲线
5 结论
1) 考虑到产品性能退化的随机性,基于随机维纳过程的寿命预测与可靠性评估方法可以更准确地描述其寿命与可靠性。
2) 基于退化轨迹模型的寿命预测与可靠性评估过度依赖于故障首发检测时刻点,在该时刻点未知的情况下,完全依赖基于退化轨迹模型预测得到的结果存在高估的可能,给产品实际使用过程中带来风险。
