在约束条件下集值全局真有效点集的连通性

刘富荣， 陈剑尘， 汪 洋

（南昌航空大学，数学与信息科学学院，南昌 330063）

引言

在集值优化问题中,全局真有效解的连通性是十分值得我们去深究的问题之一。对于全局真有效点集的标量化问题Gong在文献[1]己经进行了研究，并得到了一些重要的结论。随后，王秀玲在文献[2]对全局真有效解的概念作了详细的阐述，并将可行域设定在紧凸集的情况下，对全局真有效解集的连通性进行了深入研究。紧接着,高洁在文献[3]中将目标映射设为弱上半连续的,可行域设成弧连通紧的，证明了全局真有效点集的连通性和全局有效解集的连通性。本文首先给出了全局真有效性的相关概念和h−有效点的相关定义，并在可行域为一般非空紧子集，约束映射为上半连续且目标映射为锥类凸的情况下，在相对较弱的条件下得到了全局真有效点集连通性的定理，这就使目前全局真有效点集连通性的相关结论得到进一步推广。

1 预备知识

除特别说明外，本文始终假设X是拓扑空间，Y和Z是Hausdoff局部凸拓扑线性空间。Y的拓扑对偶空间用Y∗表示，M⊂Y为非空子集，用cl(M)表示M的闭包,conv(M)表示包含M的最小的凸集，集合M的生成锥记为:

C是Y中的闭凸点锥，且intC≠∅。C的正对偶锥C∗和严格正对偶锥C#分别定义为:

B⊆C是非空凸子集，B称为锥C的基，假如C=cone(B)且0∉cl(B)。

定义1.1[1]设D⊂Y是非空子集合，C是Y中的闭凸点锥：

1)x∗∈D称为D关于C的有效点，记x∗∈E(D,C)，若(D−x∗)∩(−C)⊂C。若C为点锥，则x∗∈D为有效点当且仅当(x∗−D)∩C={0}，当且仅当(x∗−D)∩D={x∗}。

2)称y0∈D为D的全局真有效点，记作y0∈ZE(D,C)，假设存在Y中的闭凸点锥G，C{0}⊂intG，使得

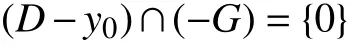
由定义，可知，全局真有效点必然为有效点，即

(3)假设h∈C∗{0}，称y0∈D为D的h−有效点，若：

此时，记作y0∈h−E(D,C)，记D的h−有效点的全体为h−E(D,C)。

定义1.2[4]设A⊆X为非空子集。集值映射F:A→2Y称作C−类凸的，若F(x)的凸包包含在F(A)+C中，即

定义1.3[1]假设D⊂Y是非空子集合，C是Y中的闭凸点锥，假设D+C为凸集，则称D为C−凸集。

引理1.1[1]假设Y是局部凸的空间，C是Y中的点凸锥，且有基B，D⊂Y且D≠∅是C−凸集，则有

假设A为X的非空子集，F:A→2Y为集值映射且∀x∈A,F(x)≠∅.设X为Hausdoff局部凸空间，我们研究下面的向量优化问题(SVOP)：

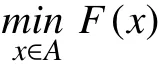
定义1.4[4]假设x0∈A,y0∈F(x0)，C为Y中的点凸锥，x0称作(SVOP)的全局真有效解，假设存在Y中的点凸锥H，C{0}⊂intH，使得

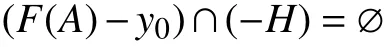
集值优化问题，关于锥C全局真有效解构成的集合记作ZE(A,C,F)。

2 全局真有效点集的连通性

设C⊂Y,T⊂Z分别是Hausdoff局部凸拓扑空间X与Y中的非空闭凸点锥。A⊂X为非空子集合，F:A→2Y，G:A→2Z为集值映射，且∀x∈A，F(x)≠∅,G(x)≠∅。

我们定义非空约束子集如下:

引理2.1[5]集值映射F:S→2Y是C−类凸集值映射当且仅当F(S)+C为凸集。

引理2.2[6]设A是X中的非空子集合，T⊂Z为闭凸点锥。集值映射G:A→2Z是上半连续的，则非空约束集S={x∈A:G(x)∩T≠∅}是闭集。

引理2.3[7]设X是局部凸拓扑空间，则A⊂X为有界集当且仅当A关于X中的弱拓扑为有界集。

定义2.1[7]设X,Y为两个拓扑空间，集值映射F:X→2Y称在x0∈X处是上半连续的,假如对F(x0)的任意的邻域V⊂Y，存在x0的邻域U，使得F(U)⊂V。称F在X上是上半连续的，若F在X上任一点处是上半连续的。

引理2.4[8]若A是X中的非空子集合，F:X→2Y为集值映射，若下面3个条件同时成立：

①对∀x∈A，F(x)为非空连通集；

②X的非空子集A为 连通集；

③集值映射F:X→2Y是上半连续的,

则F(A)为连通集。

引理2.5[9]设X和Y为2个拓扑空间，其中X为紧集，若集值映射F:X→2Y为上半连续的，且∀x∈X,F(x)为紧的，则F(X)必为紧集。

引理2.6[10-12]设X和Y是两个Hauddorff拓扑空间，G:X→2Y是集值映射x0∈X，G(x0)是紧集,则G在x0∈X是上半连续当且仅当对于X中的任意网{xα,α∈I},且xα→x0，对Y中任意网{yα,α∈I}，有yα∈G(xα),∀α∈I，都存在y0∈G(x0) 和{yα,α∈I}的一个子网使得yβ→y0。

命题2.1定义集值映射R:C#→2F(S)使得

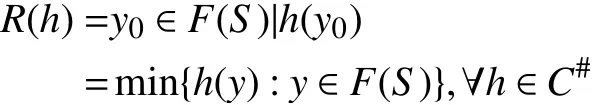
若规定C#上的拓扑为强拓扑β(Y∗,Y),F(S)上的拓扑为弱拓扑σ(Y,Y∗)，F(S)为弱紧的，则R为 上半连续映射。

证明：反证法。假设R不 是上半连续的，则存在h0∈C#，使得R在h0处不上半连续.于是存在R(h0)的弱开邻域V⊂Y，对V可取到网{hα}⊂C#及网{yα}，其中yα∈R(hα)，使得。由于{yα}⊂F(S)且F(S)为弱紧集，不妨设又yα∉V，V为弱开领域开集，故y0∉V。由

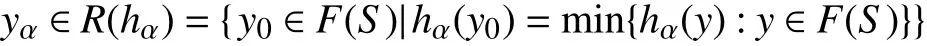
知

由于F(S)为弱紧的，故F(S)是弱完全有界的，从而关于弱拓扑有界。又(Y,σ(Y,Y∗))为局部凸空间，由引理2.3知，G为 有界集，于是PG是空间(Y∗,β(Y∗,Y))上的连续半范。于是∀ε＞0,∃α0，使得α≥α0时，有

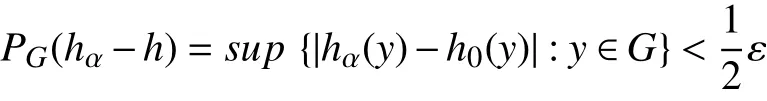
于是α≥α0时，有

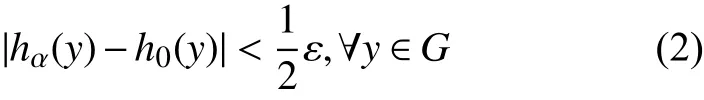
又h0∈Y∗,故h0是连续的，于是∃α1≥α0，使得

由式(2)和式(3)可得

由极限的保号性，对(1)式两边取极限得

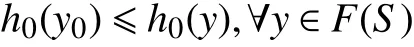
于是y0∈R(h0)⊂V，但这与y0∉V矛盾，于是R在C#上是上半连续的。

定理2.1设A为X中的非空子集且为紧集，C、T分别是Y、Z中的闭凸点锥，B是C的有界基，在非空约束集S上的目标集值映射F:A→2Y为C−类凸的，在S上取弱紧值且是上半连续的(这里Y上的拓扑是弱拓扑σ(Y,Y∗))，约束映射G:A→2Z为上半连续的，其中非空约束集S={x∈A:G(x)∩T≠∅}。则ZE(F(S),C)是非空连通集。

证明：由引理2.2知A中非空约束集S为闭集，又A是紧集，故S也是紧集。因为F是上半连续映射(其中Y上的拓扑为弱拓扑σ(Y,Y∗)，且F在S上取到弱紧值，故由引理2.5知，F(S)是弱紧集。又F为C−类凸的，由引理2.1知，F(S)+C为凸集。因为Y为局部凸空间，C为闭凸锥且具有基B，由引理1.1可知

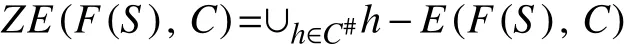
任取h∈C#，由于h关于弱拓扑σ(Y,Y∗)连续，且F(S)关于拓扑σ(Y,Y∗)为紧集，故∃x0∈F(S)，使得

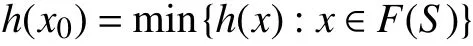
即h−E(F(S),C)≠∅. 从而ZE(F(S),C)≠∅。

下证ZE(F(S),C)的连通性：

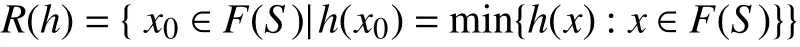
易知

由F(S)为弱紧集知，对∀h∈C#,R(h)≠∅。又C#为凸集，故C#为连通集。

任取x1,x2∈R(h),则x1,x2∈F(S)，且由R(h)的定义可知

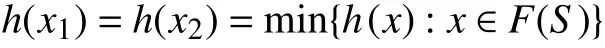
h∈Y∗∀t∈[0,1]

由于为连续线性泛函，故对，有

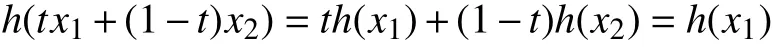
下面说明tx1+(1−t)x2∈F(S),∀t∈[0,1]。若不然，存在t0∈[0,1]，使得

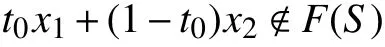
由于F(S)+C为凸集，且x1,x2∈F(S)，故存在x3∈F(S),c∈C使得

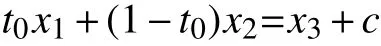
若c=0，则有t0x1+(1−t0)x2=x3∈F(S)

这与假设矛盾，故c≠0。此时h(c)＞0，于是由h∈C#

可得

这与

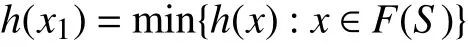
矛盾。

于是

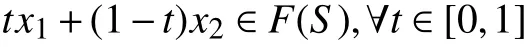
从而tx1+(1−t)x2∈R(h),∀t∈[0,1]。即R(h)，∀h∈C#为非空连通集。

于是由命题2.1以及引理2.4可得∪{R(h):h∈C#}连通集，从而ZE(F(S),C)是非空连通集。

3 结论

本文将可行域A设定在非空的一般紧子集上，在约束映射G是上半连续的且约束集上的目标映射F是上半连续的锥类凸的情况下, 通过对对偶锥上的集值映射连通性的证明,对含约束锥类凸的全局真有效点集的连通性进行了讨论，并给出了相关结论，故本文是在条件相对较弱的目标映射及可行域更一般的条件下推广了现有的集值优化问题全局真有效点集连通性的有关结论。