含薄层区域上的一类等值面边值问题解的极限性态

肖美萍， 陈凌蕙， 邹维林

（南昌航空大学 数学与信息科学学院，南昌 330063）

引言

偏微分方程的等值面边界值问题在70年代被提出[1-2]，此类模型问题来源于很多实际问题的需要，特别是可以模拟石油开发中电阻率测井模型。关于线性偏微分方程的等值面边界值问题，已经得到较为深入的研究[1-4]。近年来，对非线性偏微分方程的等值面边界值问题的研究也已取得较大进展[5-9]。此外在石油测井中，人们也经常遇到一个裂缝岩层区域，由此可以建立含薄层的区域上的等值面边界值问题。在用有限元方法进行数值计算时，特别是当计算到该薄层区域时，需要加大量的节点，这就增加了计算工作量，有时还会产生较大的误差。为了克服此困难，在实际计算中很自然会考虑能否把原来的问题近似为一个没有薄层区域的较简单的问题来处理。因此，这就需要研究此类问题的极限性态。对于线性椭圆方程的情况，这一问题已得到解决[4]，拟线性强制椭圆问题的研究也已经有部分结果[9]。本文主要的目的就是将以往的研究结果[4,9]推广到非线性退化椭圆情况，且自由项仅为L1可积。

具体来说，主要研究下列问题解的存在唯一性与极限性态：

这里Ω是RN(N≥2)中以曲面Γ为边界的有界光滑区域（如图1），且Ω分解成3个互不重叠的区域，和Ω，其交接面分别为与，且是一个薄层区域。

图1

为了研究问题(Pε)解的极限性态，需要从数学上刻画薄层区域当ε→0时的极限（收缩为曲面），亦即满足假设条件：

(H1)对任意给定且当ε→0时，

(H2)对任意给定的满足时，则当ε充分小时，有(P)

另一方面，还需要研究下面的等值交接面问题

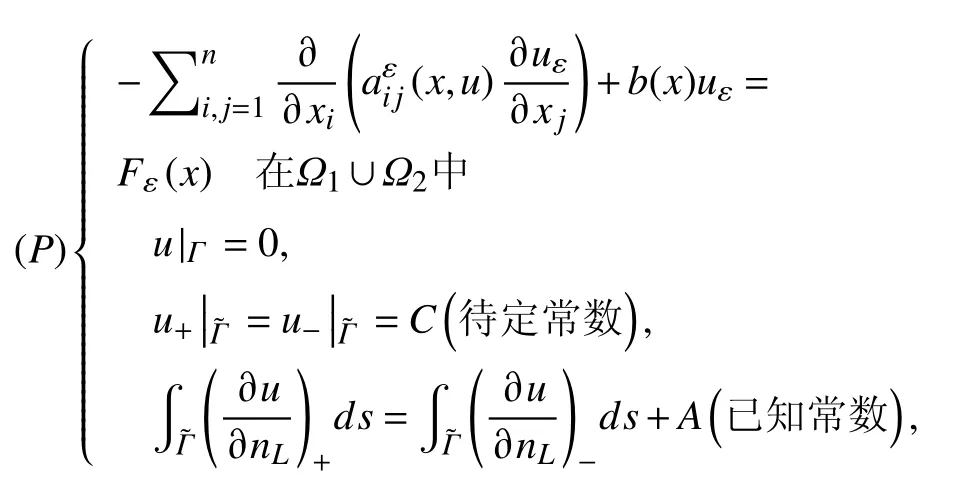
其中

区域Ω由Ω1和Ω2组成，为其交接面，Γ为Ω的边界，如图2所示。

图2

1 假设条件与主要结果

定义1.1一可测函数uε∈Vε，称为问题(Pε)的弱解，如果对∀v∈Vε满足

为得到问题(Pε)的弱解的存在唯一性，需要系数以及自由项Fε(x)满足如下假设条件：对a.e.x∈Ω和∀s∈R都 成立，且存在常数α＞0满足：

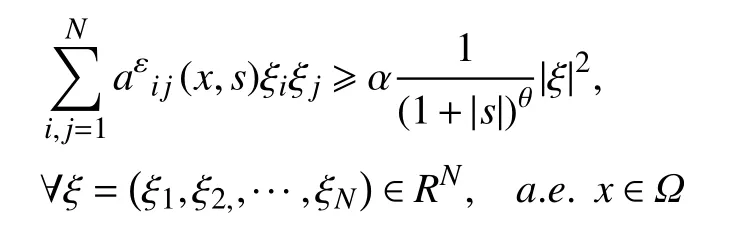
(H4)(x,s)为Ω上的可测函数，(x,0)∈L∞(Ω)，且对∀ε＞0存在一个与 ε无关的常数β＞0，使得

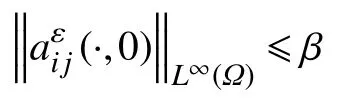
(H5)存在非负函数h(x)∈L∞(Ω)，使得

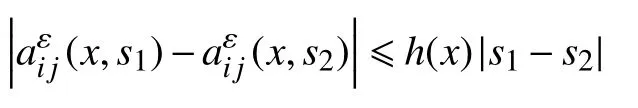
(H6)假定Fε∈L1(Ω), 非负函数bε∈L1(Ω)，且存在正常数 Γ与非负函数f∈Lq(Ω)（常数）使得

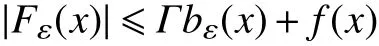
注1.2条件(H3)意味着当解u趋于无穷时，方程的主算子趋于零，亦即当解u趋于无穷时，扩散现象消失。这些方程可用来刻画产生饱和效应的反应模型[10,11]。

基于上述假设条件，可以得到本文的第一个主要结果（问题(Pε)的弱解的存在唯一性）：

定理1.3设条件(H3)−(H6)成立，则问题(Pε)的弱解的存在唯一的弱解uε∈Vε∩L∞(Ω)，且存在与ε无关的正常数M满足

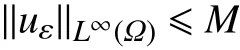
定义1.4一可测函数u∈V，称为问题(P)的弱解，如果对∀v∈V满足

为证明问题(Pε)的弱解uε收敛于问题(P)的弱解u，需要对系数(x,s)，bε(x)以及自由项Fε(x)的极限性态做如下假设：

(H7)对当时有在中几乎处处收敛，且关于s是一致连续。

(H8)对，当时有，bε(x)→b(x) 在中强收敛。

(H9)对当时有，Fε(x)→F(x)在中强收敛。

上述条中的极限函数aij(x,s)，b(x)以及F(x)满足如下假设条件：

(H10)aij(x,s)=aji(x,s)对a.e.x∈Ω和∀s∈R都 成立，且存在常数α＞0满足：

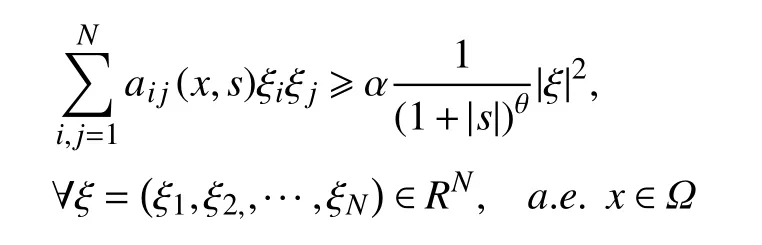
(H11)aij(x,s)为Ω上的可测函数，aij(x,0)∈L∞(Ω)，且存在常数β＞0，使得

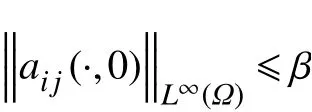
(H12)存在非负函数h(x)∈L∞(Ω)使得对任意s1,s2∈R

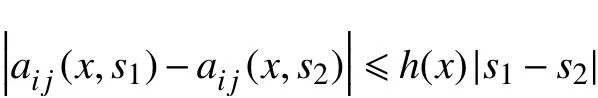
(H13)假定F∈L1(Ω)，非负函数b∈L1(Ω)满足

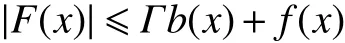
基于上述假设条件，可以得到本文的第2个主要结果（问题(Pε)的弱解的存在唯一性）：

定理1.5设条件(H1)−(H13)成立，uε∈Vε∩L∞(Ω)为问题(Pε)的唯一弱解，u∈V∩L∞(Ω)为问题(P)的唯一弱解。则有

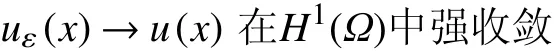
2 主要结果的证明

定义

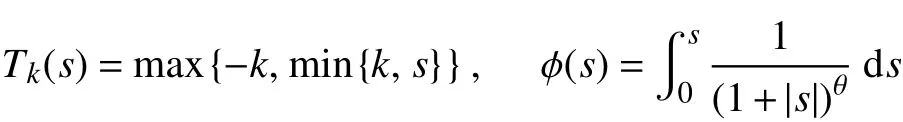
为了叙述方便，本文中将用Ci(i=1,2...)表示与n,ε无关的常数。

定理1.3的证明：主要分为存在性与唯一性两步进行。

第一步：存在性的证明。

定义

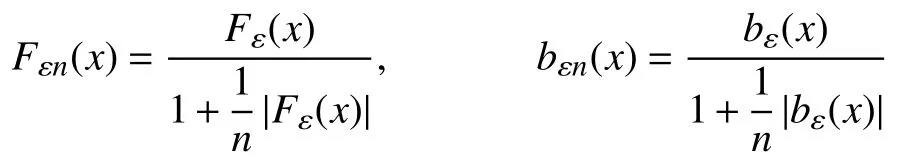
现在引入如下逼近问题

其中IN为N阶单位矩阵。

类似于定理3.1[5]的证明，可知对任意固定的n≥1，问题(Pεn)存在唯一的弱解uεn∈Vε，使得

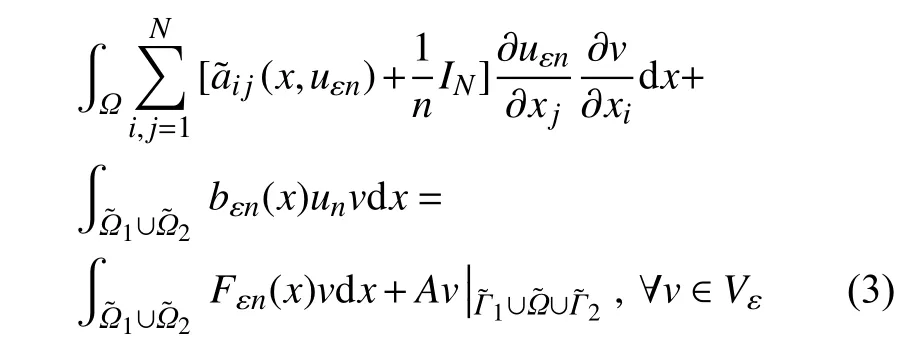
对任意k＞0，在式(3)中取v=(|ϕ(uεn)|−k)+sgn(uεn)，由条件(H3)可得

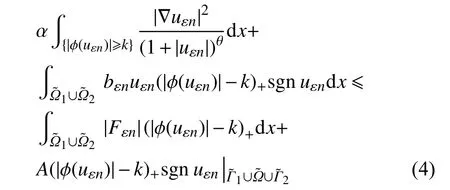
利用条件(H6)可得到

根据引理3.2[5]可得

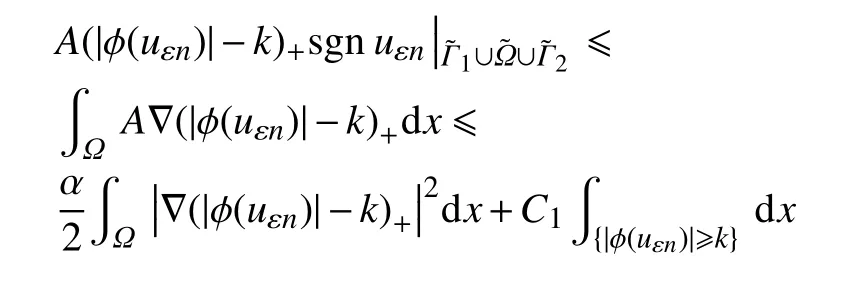
将以上两式代入式(4)中，立即得到

进一步在式(5)取k＞ϕ−1(Γ)，可得

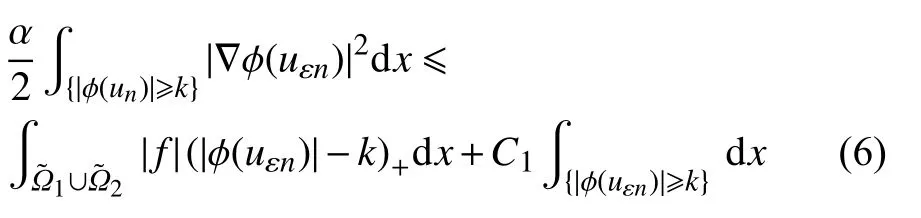
接下来可以利用经典结果[12]，可知

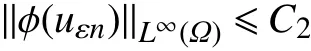
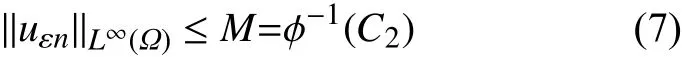
在式(3)中取v=uεn，由条件(H3),(H6)和式(7)可得

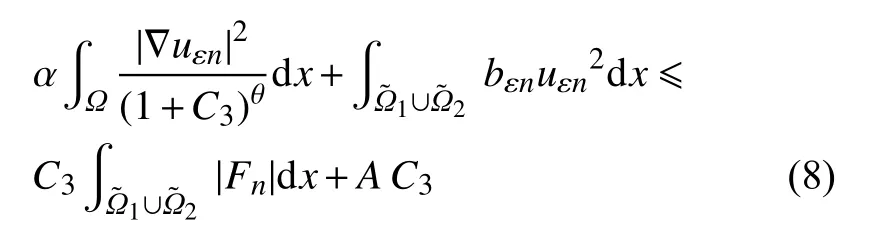
根据式(7)和式(8)可知存在uεn的一个子列（仍用uεn表示）和一个函数当n→+∞，有以下结果：

利用经典方法[13]，可以得到

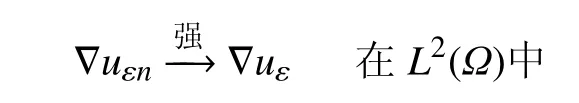
在式(3)中令n→+∞立即得到函数L∞(Ω)为问题(Pε)的解，且有

第二步：唯一性的证明。

现假定uε,wε∈Vε为问题(Pε)的两个弱解，则由弱解定义知，uε,wε满足

在式(9)和式(10)中取v=Tk(uε−wε)，两式相减得到

进而利用假设条件(H3)～(H5)容易得到

利用勒贝格控制收敛定理，上式意味着

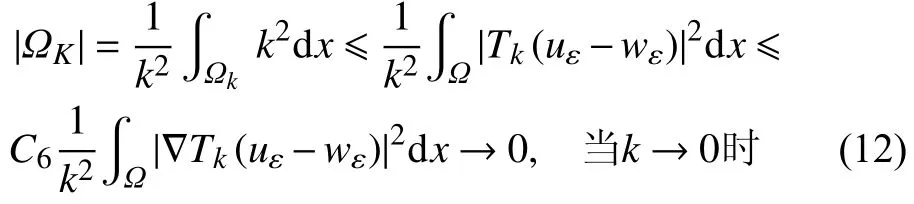
因为k→0时，故有。因此uε(x)=wε(x)在Ω中几乎处处成立。唯一性得证。

定理1.5的证明：因为为问题(Pε)的唯一弱解，由定理1.3的结果可得uε满足式(1)，且有

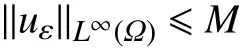
在积分等式(1)中取v=uε，容易得到

根据上述2个估计可知存在uε的一个子列（仍用un表示）和一个函数当ε→0有以下结果：

再一次利用经典方法[12]，可以得到

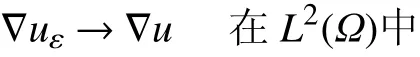
在式(1)中令ε→0，利用上述收敛结果与假设条件(H1)−(H2)和(H7)−(H9)，立即得到函数u∈为问题(P)的解。

另一方面，类似于定理1.3的证明，利用假设条件(H10)−(H13)可知问题(P)的有界弱解存在且唯一。定理证毕。

3 结论

1）主要研究了一类含薄层区域上的非线性退化椭圆型等值面边界值问题，在自由项与零阶项的系数均为L1可积并满足一定的相关性条件下证明了问题有界弱解的存在性与唯一性。

2）假定方程的系数与自由项与零阶项的系数满足一定收敛条件，当薄层区域收敛于一曲面时，证明了原薄层区域上问题的解收敛于一类等值交界面问题的弱解。

3）当薄层区域厚度充分小时，在实际计算中可以将薄层区域上的等值面问题近似为一个不含薄层区域的等值交界面问题来处理。