让学生经历“开放探索”的过程

黄英俊

【摘要】学生是学校教育活动的主体，学生的主体能动性强弱决定了教育教学的成败，但教学中应如何调动、发挥学生主体性，却是教师一直努力追求的方向.多年来，笔者在教学中开展了“开放探索”的训练，以更好地发挥学生的自主性，提高学生学习数学的能力.下面笔者以“反比例函数k的几何意义”为例整理成文，期盼得到大家宝贵的指导建议.

【关键词】主体性;开放探索;数学改进

一、教学中存在的困惑

“反比例函数k的几何意义”是湘教版九年级下数学的教学提高内容，它很好地体现了“数形结合”思想方法的运用.对该内容的教学，笔者大体上设计了三个环节：

环节1：设计2道填空题：由反比例函数（2道题的k值分别是6和-4）图像上的一点分别向坐标轴作垂线，则它与坐标轴所围成的矩形的面积为.在此基础上，教师概括出一个结论，从而引出课题.

环节2：设置2道例题精讲，4道练习巩固.

环节3：师生课堂小结，布置课后作业.

课堂结束后，从“练习巩固”“课后作业”的反馈来看，学生完成中档题的正确率较高，对此知识已经能够较好地掌握.

但是，在做“反比例函数”的综合题时，学生出现一些问题，比如，所求图形面积究竟是k，还是|k|？是|k|，还是|k|[]2？特别是不知道何时运用“反比例函数k的几何意义”，更不知道为什么会这样想.究其原因，是学生对“反比例函数k的几何意义”的图形结构特征的本质认识不到位造成的.

二、教学改进后的课堂设计

再次讲授本节课时，笔者仍采用原有教学设计环节1的两个问题.

问题1：如图1，已知点A在反比例函数y=6x的图像上，AB ⊥ y轴于点B，AC⊥x轴于点C，则阴影部分S矩形ABOC的面积为.

问题2：如图2，已知点A在反比例函数y=-4x的图像上，AB ⊥ y轴于点B，AC ⊥x轴于点C，则阴影部分S矩形ABOC的面积为.

在解决这2道填空题时，教师强调求解的中间关键过程，设A（a，b），S矩形ABOC=OC·AC=|a|·|b|=|ab|，其关键就是利用线段与点的坐标的关系.随后，教师并没有直接给出一般结论，而是让学生思考：你们能进一步提出什么问题吗？学生可以提出：如果我们将解析式y=6x或y=-4[]x变化为一般式y=k[]x（k≠0），其结果有怎样的规律呢？

有了前面的基础，学生可以独立思考，容易计算出结果并发现规律：由反比例函数y=kx（k≠0）图像上的一点分别向坐标轴作垂线，所围成的矩形的面积均为|k|.由此引出课题.

教学到此，笔者并没有带领学生进入例题环节，而是提出了两个开放性的问题：

（1）你能画出一个在反比例函数y=6x的图像中的图形，并求出它的面积吗？想一想，画一画，写一写.

（2）把各自画的图形给小组的其他同学做一做，并说出你是怎样画出图形的，又是如何求出图形的面积的.然后选出本组认为最有代表性的图形在班级进行交流分享.

（明确任务后，学生独立思考，教师巡视）

等各小组组内交流后，教师组织学生进入班级交流分享环节.

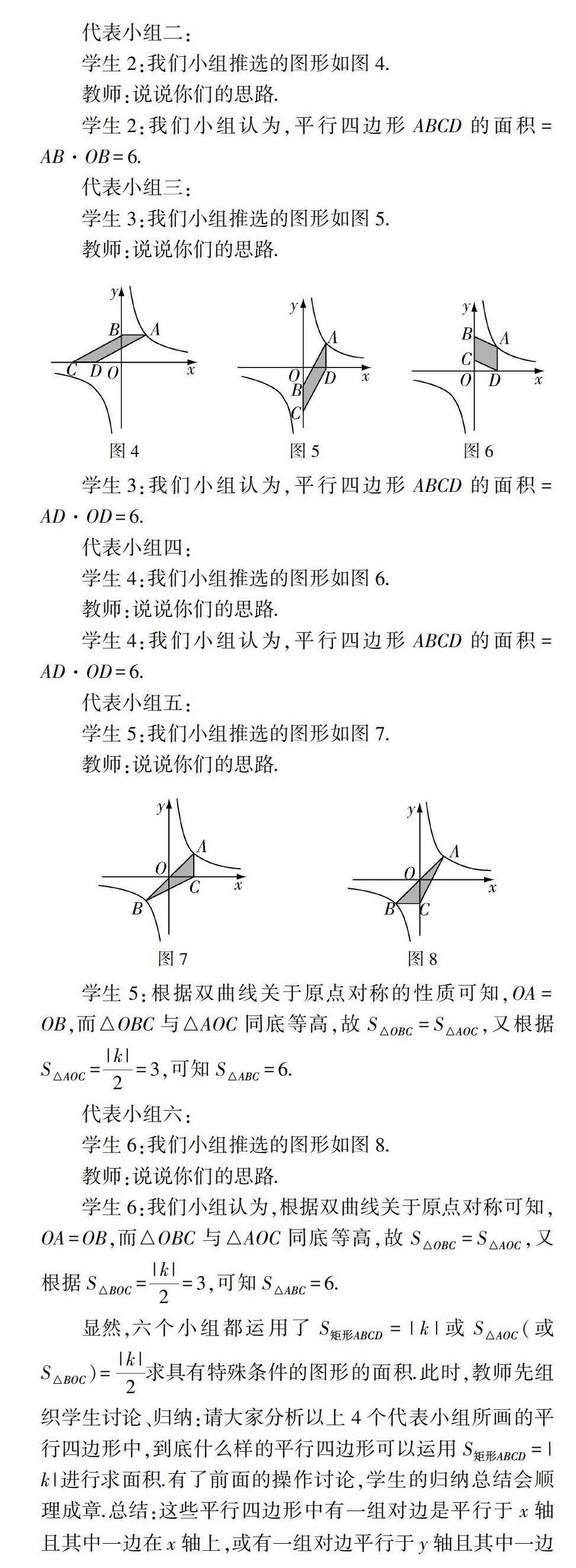
代表小组一：

学生1：我们小组推选的图形如图3.

教师：说说你们的思路.

学生1：我们知道平行四边形的面积是底乘高.

教师：你们是以哪一边为底？随便以哪一条边为底都可以吗？

学生1：我们是以AB或CD为底，以OB为高，而不是随便以哪条边为底.

代表小组二：

学生2：我们小组推选的图形如图4.

教师：说说你们的思路.

学生2：我们小组认为，平行四边形ABCD的面积=AB·OB=6.

代表小组三：

学生3：我们小组推选的图形如图5.

教师：说说你们的思路.

学生3：我们小组认为，平行四边形ABCD的面积=AD·OD=6.

代表小组四：

学生4：我们小组推选的图形如图6.

教师：说说你们的思路.

学生4：我们小组认为，平行四边形ABCD的面积=AD·OD=6.

代表小组五：

学生5：我们小组推选的图形如图7.

教师：说说你们的思路.

学生5：根据双曲线关于原点对称的性质可知，OA=OB，而△OBC与△AOC同底等高，故S△OBC=S△AOC，又根据S△AOC=|k|[]2=3，可知S△ABC=6.

代表小组六：

学生6：我们小组推选的图形如图8.

教师：说说你们的思路.

学生6：我们小组认为，根据双曲线关于原点对称可知，OA=OB，而△OBC与△AOC同底等高，故S△OBC=S△AOC，又根据S△BOC=|k|[]2=3，可知S△ABC=6.

显然，六个小组都运用了S矩形ABCD=|k|或S△AOC（或S△BOC）=|k|[]2求具有特殊條件的图形的面积.此时，教师先组织学生讨论、归纳：请大家分析以上4个代表小组所画的平行四边形中，到底什么样的平行四边形可以运用S矩形ABCD=|k|进行求面积.有了前面的操作讨论，学生的归纳总结会顺理成章.总结：这些平行四边形中有一组对边是平行于x轴且其中一边在x轴上，或有一组对边平行于y轴且其中一边在y轴上;还发现求这些平行四边形的面积都是利用同底等高转化为图1所示矩形的面积.

继续探索，反比例函数图像中什么样的三角形的面积也等于|k|？

以上处理经历“开放探索”，明显比教师直接归纳的耗时要长，但学生比以往更加主动，更能积极思考，对这些特殊图形的特征结构更能深入理解，更能有效地化解难点.

三、前后教学实践的对比分析与反思

1.此前的教学，教师更习惯直接给出结论

在以往的教学中，为了节省时间，对某些重要结论的教学，有些教师往往是快速给出结论，然后挤出时间让学生练习更多的题目.像本案例中的教学环节1，师生一起计算2道填空题，然后很快总结得出结论，再对结论进行记忆.这样的做法，课堂组织很顺畅，效果也不错，但是，学生对知识只停留在简单的记忆中，对其本質没有深入理解，无法自主建构知识，从而造成在综合运用中难以熟练变通.这样的教学，只会让学生不断地被动接受知识，使学生对数学学习的兴趣逐渐减弱，不能激发学生的学习热情.

2.此前的教学，教师更多地“牵手”

在以往的教学中，有些教师总是认为学生的思维水平不如教师.所以，教师总是千方百计在前面牵着学生走，带领学生一问一答去解决问题，这样做没有激发学生、助力学生，反而使学生养成了不爱动脑的坏习惯.久而久之，教师教得累，学生学得苦.为此，教师时常发出“明明是讲过了，学生就是不会”的感慨与无奈，以致教师的身心付出换不回高效的教育效果.

3.本次教学，教师更注重结论的生成过程

课堂的主体是学生，教师应当努力将课堂教学变成学生自主学习、合作交流、创造知识的一种学习方式，让学生思知识的来龙去脉，说问题的逻辑推理，悟数学的思想方法.学生独立思考，培养研究精神;学生合作探究，优化思维过程;学生自主创造，提高学习能力.所谓注重结论的生成过程，就是教师要在知识的形成过程中，启发学生的疑处，鼓励学生大胆探索，激发学生的学习热情，对知识生成过程不惜时、不惜力，从而使学生达到真正意义的理解性学习.

4.本次教学，教师更多地“放手”

数学教育“应给学生自己发现事物的机会”“学习任何知识的最佳途径是亲自去发现”.所以，教师应当把课堂的主动权还给学生，让学生当“主角”，教师当好教学活动的组织者、学生发展的促进者.教师完全可以大胆地放手给学生去创造，让学生经历“探—悟—再探—再悟”的循环过程，进而直达数学的本质、核心，使得知识、技能、方法得以落实，这样的过程，教师无须替代，只需为学生的长远发展保驾护航.

结束语

教学中，教师可以把每次的数学活动组织成有“美丽看点”的旅行，激发学生“火热”的思考，让学生享受数学课堂，生成数学智慧.