分层教学视阈下“圆与相似”教学设计研究
2021-05-31张嫌
张嫌
【摘要】新课程基本理念指出:数学课程应致力实现义务教育阶段的培养目标,要面向全体学生,适应学生个性发展的需要,使得人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.在新课程改革背景下,教师如何教、教学如何实施、学生如何学、如何提升学习效率是教师和学生面临的难题.本文通过讨论如何分层教学圆与相似这节复习课,回答上述问题,从而培养学生“用眼看、动脑想、大胆猜、严格证”的几何直观能力,让每名学生都有所收获.
【关键词】分层教学;圆与相似;教学设计
古希腊数学家毕达哥拉斯认为“一切平面图形中最美的是圆”.圆具有独特的对称性,同时具有较多的性质与定理.在教学中,教师应有意识地将圆与其他几何、代数知识进行横纵联系,形成知识体系,帮助学生感知数学内容之间的内在联系,从而达到整体性认识.本文依据圆与相似三角形的结合,让学生体会相似三角形在处理圆中求比例中项、等积式、线段长度的独到之处.
借鉴孔子提出的“因材施教”教学理念,以及王守仁提出的“随人分限所及”教育原则,教师在数学课堂中采用分层教学方式,让学生“人人皆学,处处能学,时时想学”.分层教学主要指教师根据学生的能力、兴趣和爱好等多方面的差异,进行分层次教学,以满足不同学生的发展需求.分层教学的指导思想:要求教师尊重学生的个体差异,甄选适合学生学习和发展的教学方式进行授课教学.分层教学主要包括学生分层、目标分层、教学分层、练习分层、评价分层、反思分层六个方面.
一、教材分析和学情分析(学生分层)
本文的教学设计内容是人教版九年级数学上“第24章圆”与九年级数学下教材中“第27章相似”的融合,是在学习了有关相似三角形和圆的知识的基础上,引导学生利用圆的性质,多角度寻找构成相似三角形的条件;掌握在圆中求比例中项、等积式、线段长度的方法;巩固圆与相似三角形的判定与性质,为几何证明提供一些方法;渗透转化、类比、数形结合、方程的思想,提升学生的逻辑推理能力,深入挖掘知识间的联系,发展学生的数学核心素养.
本文是在学生刚刚学完切线长定理的基础上进行的教学设计.九年级学生已具有一定的分析能力和逻辑推理能力,由于学生个体差异较大,所以为了尽可能关注到每一名学生的发展,教师宜采取分层教学手段:先将学生分层,根据范希尔几何思维理论,分析出各层次学生的几何思维水平,资优生分为A组(理论水平),中等生分为B组(描述水平),潜能生分为C组(直观水平),并在组内继续从低到高再排列.教师需要在分组上下功夫,多了解学生,关注到每一名学生.分组具体情况只有教师自己知道,避免有些学生知道分组情况后感到失落.教师可以告知学生组内人员情况不是固定不变的,而是灵活调整的,表现较好的同学可以向上一层移动,学生状态不佳的可以往下降一级,根据各个阶段的学习情况来决定,这样就会形成良性竞争的学习氛围.
二、教学目标(目标分层)
1.整体教学目标
知识与技能:根据圆的性质,了解圆中找相等角的方法,能在圆中运用这些方法识别相似三角形;掌握圆中相似三角形的几种基本模型,并能加以应用解决相关问题.
过程与方法:通过问题探究及思考,经历猜想、推理、验证等环节,抽象出圆中相似三角形的基本模型,尝试从不同角度解决问题并在反思中获得解决问题的方法.
核心素养:通过探究、思考、练习,培养学生“用眼看、动脑想、大胆猜、严格证”的几何直观能力;在知识迁移中体验转化、类比、数形结合、方程的数学思想,强化问题意识,培养学生的逻辑推理能力,增强思维的延展性,形成相应的思维链.
2.各个层次教学目标
A层:能将圆与相似三角形知识系统化,灵活应用圆中找等角的各种方法,学会多角度思考问题,能养成开放性、缜密性思维.
B层:熟练应用圆中找等角的方法,能在圆与相似的情境中求解线段长度、比例式、等积式,学会思考,提出见解.
C层:掌握圆与相似三角形的知识,学会在圆中找等角并能够识别圆中的相似三角形,理解知识间的联系.
三、教学重点
灵活应用圆的性质,发现圆中的相似三角形,掌握圆与相似的基本模型并能解决相应问题,学会圆中线段长度、比例式、等积式的求法.
四、教学难点
分析确定圆中的相似三角形,掌握圆中寻找相似三角形的方法.
五、教学方法
针对九年级学生的年龄特点和心理特征,结合学生的认知水平,以分层教学法为主,以练习法、类比探究式教学法为辅.
六、教学手段
希沃白板,PPT,三角尺.
七、教学过程(教学分层)
(一)课前练习及探究
圆的内容比较多,一开始讲圆与相似有些突兀.教师可借助问题引入,让学生在解答过程中遇到认知障碍,需要寻求新的解决方法,这时引导学生回顾三角形相似的判定方法、基本模型以及性质,从横向(平行、两角相等)、纵向(A字型、8字型、双垂模型)两个维度回顾旧知,再將圆与相似结合,从而为后面学习奠定基础.这样从学生的认知发展出发,过渡自然,易于学生接受.在练习过程中,教师可观察学生的完成情况,对不同层次的学生进行提问,检测各层次学生的掌握情况.
(二)思考
思考一:同弧或等弧所对的圆周角相等
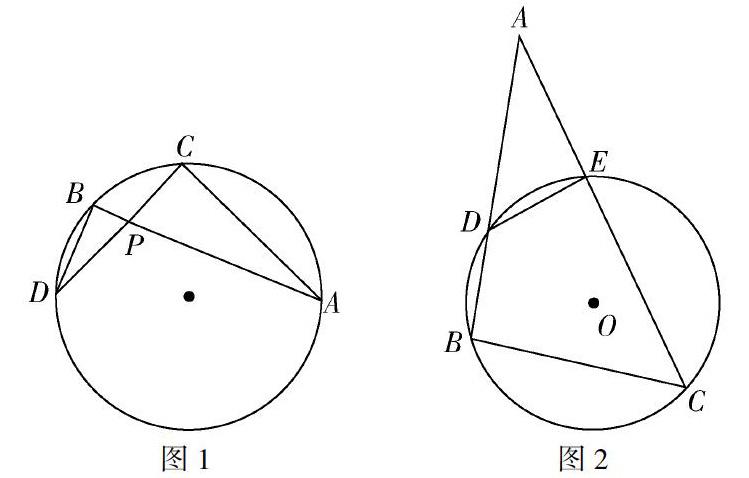
如图1,△APC∽△DPB吗?
思考二:圆内接四边形一个外角等于它的内对角
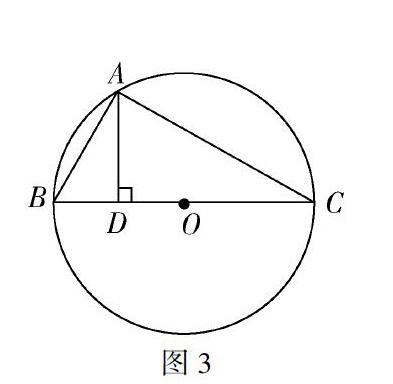
如图2,△ADE∽△ACB吗?
思考三:由垂径定理找等角
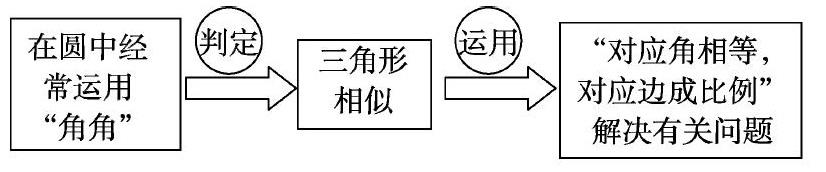
如图3,已知BC是⊙O的直径,且AD⊥BC,△ABD∽△CBA吗?
你还能得到哪几个三角形相似?
【设计意图】教师在讲授完课前练习后,抛出这三个思考题,让三个层次的学生按提前分好的小组进行讨论交流(三个层次学生的座位是交叉的,一个A层次学生可带一至两个B,C层次学生,每个小组内有“领头羊”,讨论交流时要有组织地进行,每个组大概有五至六人),从中抽象出圆与相似的基本模型.随着知识螺旋上升,学生的形象思维上升到抽象思维.教师让学生体会在圆中找等角的方法,并且,在与相似三角形的对比中加深在圆中找相似三角形的思路,激活学生原有的认知结构,让学生在尝试探索中挖掘内在潜能,从而培养学生的发散性思维.
(三)典例精讲
教师带领学生理清几何证明思路,规范书写步骤,巩固复习切线的判定(有切点连半径、证垂直,无切点作垂直、证半径)及性质定理(有切点连半径得垂直),从分析法和综合法入手,发展学生的逻辑推理能力,灵活应用圆与相似的求解方法;教师从三个层次的学生中挑三名学生的作业在希沃白板上展示,检查他们的掌握情况,再挑选不同层次的学生回答问题,采用“说数学”的方法,利用出声思维,强化对概念的理解.对比三个层次学生间的差异,教师对学生的解答给予适当的评价.
(四)巩固练习(练习分层)
刚刚学完圆与相似三角形的知识,不同层次的学生掌握的情况也不同.学生使用的教辅大部分都进行了分类处理,即分为基础题、中档题、综合题,教师可以选择性地使用,针对学生分层次布置作业避免卷成海、题成宗.例题、习题的选择要根据学情确定,做到精致练习,这就减轻了学生的学业负担,学习效率自然而然也得到了提升.
(五)课堂小结
圆中找等角的方法:(做辅助线构造)
1.同弧或等弧所对的圆周角相等
2.由垂径定理找等角
3.结合三角形外角、内角等知识综合演绎
4.利用圆与相似三角形综合解题
【设计意图】教师引导学生对该内容进行归纳总结,让学生掌握圆与相似的综合解题思路,做到以不变应万变,真正领略其本质,使学生养成“学习—总结—反思—学习”的良好习惯,培养学生归纳、概括的能力.
八、评价分层
针对整个教学过程,教师根据学情对学生学习结果进行评价,做到评价分层.其主要分为三个阶段:一是过程性评价.每名学生是否都积极参与到学习活动中(可进行学生自评、互评,教师点评),掌握学生所采用的学习方法是什么,学到了什么程度.二是结果性评价.最后查看学生的巩固练习题完成情况,每个层次的学生是否均达到了预期目标.三是个别性评价.针对学生的学习情况将学生的表现进行分类,挑出几个特别的再评价.教师长期使用分层教学法教授时,应建立一个“学习动态档案”,记录学生的各个模块学习情况,然后点对点逐个提升.
九、反思分层
叶澜教授说:“一个教师写一辈子教案难以成为名师,但如果写三年反思则有可能成为名师.”可见教学反思的重要性.反思的內容很多,可以从教师的开放度、学生的参与度、教材的深透度三个方面进行思考,也可以从课前、课中、课后三个层面去思考,依情况而定.
该教学设计就“三度”来说,教师有的放矢,依据学情而定,设置小组讨论模式让每名同学都能参与课堂,关注到学生个体的差异性.教学内容的选取来源于教材又高于教材,从整体到局部;教学环节从知识的形成、建立到应用展开;教学目标设计从课程标准中来,到学情中去,安排布置比较完善,建立新旧知识间的联系,重点、难点均有体现.
为了能让学生积极参与,并且让不同层次学生在同一节课中都有所收获,教师可以在课前、课中、课后设置一定量的练习,既能随时检测学生的学习状态,又能开展课程,在练习中找到通性通法,让学生学得容易,学得轻松,学得愉快.
【参考文献】
[1]中华人民共和国教育部.义务教育数学课程标准:2011年版[M].北京:北京师范大学出版社,2012.
[2]王娅.高中数学分层教学的研究[D].武汉:华中师范大学,2018.
[3]罗新兵,王光生.中学数学教材研究与教学设计[M].西安:陕西师范大学出版总社有限公司,2011.
[4]李承兰.分层教学在中学数学课堂教学中的应用研究[J].数学学习与研究,2020(01):30.
