基于核函数强化学习的抗干扰频点分配

江志炜, 黄 洋,2, 吴启晖,*

(1. 南京航空航天大学电磁频谱空间认知动态系统工信部重点实验室, 江苏 南京 211106;2. 东南大学移动通信国家重点实验室, 江苏 南京 211189)

0 引 言

近年来,随着无线通信技术迅猛发展,无线通信系统中的用户数与业务种类大幅增加[1]。同时,在现代战争中,伴随着作战双方对安全、稳定的信息传输及处理能力需求,战场用频装备与日俱增,致使战场电磁频谱环境愈发复杂多变[2-3],因此对电磁频谱空间的控制已成为决定战场发展方向的关键性因素。战场电磁频谱态势是现代战争中信息获取和传递最主要媒介,是双方控制与反控制的焦点。由于无线通信系统区别于有线通信网络,有线通信网络中通信设备通过电缆等物理设备相连接,而无线通信网络口中接口是开放的。正是由于无线通信系统特有的开放性,无线传输自然更容易受到来自对方的恶意干扰攻击[4],因此抗干扰技术的研究在构建更加稳健、高效的无线通信系统中的重要性日益凸显。更加稳健的无线通信系统是现代战争中能否取得胜利的关键要素,因此抗干扰技术是军事无线通信系统中的重要要求[5]。主流的传统抗干扰技术包括跳频扩频(frequency hopping spread spectrum,FHSS)和直接序列扩频(direct-sequence spread spectrum,DSSS)[6],而传统的抗干扰技术需要有大量的可用频谱资源作为抗干扰技术的支持,在无法提供大量频谱资源时抗干扰效果会下降,并且传统的抗干扰技术无法应对网络频谱动态变化的场景[7-8]。

智能抗干扰决策技术由于相对于传统的跳频等抗干扰技术具有更强的灵活性与更高的抗干扰容限而逐渐受到关注[7]。近年来出现了很多针对智能抗干扰决策技术的研究,博弈论等数学工具被越来越多地用于智能抗干扰决策的研究[9-10],用以建立更加契合实际的模型并获取更好的决策效果。文献[9]将抗干扰问题建模为斯坦伯格博弈,并进行抗干扰功率决策研究。文献[10]将用户与干扰用户建模为抗干扰的贝叶斯斯坦伯格博弈模型。但这些方法需要了解干扰策略,这意味着需要合法用户能从观察到的环境中估计干扰模式和参数。但是,随着人工智能和通用软件无线电外围(universal software radio peripheral, USRP)设备[11]的快速发展,无线通信动态环境愈发复杂,干扰源攻击用户时可以轻松地产生动态干扰。因此,需要针对动态和未知环境中异构用户的抗干扰通信方法进行研究。

近年来,强化学习不仅在机器学习中,而且在运筹学、控制工程以及其他相关学科中,都吸引了许多研究者的兴趣[12]。在强化学习中,代理与未知环境进行交互,在获得回报的同时更新其策略以最大化累积收益。因此，强化学习提供了一种通用的方法来解决复杂的不确定性决策问题,这些问题在无线通信系统的抗干扰问题中是非常具有挑战性的，是解决动态和未知环境中异构用户决策问题的有效方法[13]。Q学习算法是一种无模型的强化学习算法,并且广泛应用于无线通信系统的抗干扰问题中[14-16]。文献[14]研究提出了一种基于Q学习的特定的强化学习算法,并且在数百兆赫兹的可用频段上实时地做出抗干扰策略。文献[15]研究中次级用户使用SARSA(state-action-reward-state-action)算法来学习频点的时变特性以及外部干扰的干扰策略。文献[16]研究提出了一种基于强化学习的抗干扰方法,用于在多智能体的宽带自主认知无线电(wide-band autonomous cognitive radios, WACR)环境中进行抗干扰通信。但是,通常在复杂电磁环境下的抗干扰频点分配问题的动作空间及状态空间都非常巨大,因此基于传统强化学习技术对抗干扰频点分配问题进行求解时会面临维度诅咒等问题[17]。为了解决传统强化学习技术在求解复杂不确定性决策问题时复杂度过高的问题,基于神经网络或隐马尔可夫模型等的预测模型在研究中被提出,但上述模型往往需要大量的计算资源来训练,并且需要经常定期重新训练,同时需要大量参数来获取相关的通信环境[18-19]。此外,基于深度学习的模型往往对噪声[20]和对抗[21]敏感,因此在具有业务延迟要求等的实际无线通信网络中,需要开发可以实时分析相关数据,以便为决策的制定提供参考。

本文针对雷达通信一体化系统的抗干扰问题,提出了基于核函数强化学习的抗干扰雷达-通信频谱协同算法,旨在最大化用频设备接入未被干扰频点的期望。用频设备根据可用频段的频谱态势构建出本地的频谱池,进而用频设备可以不需要预知外部干扰的干扰模式和相关参数,基于所提算法低复杂度地做出抗干扰频谱决策。因此,所提算法是无模型的,可以广泛用于各种抗干扰方案。所提算法通过基于核函数的方法,避免了随可用频点数目增加而出现的维度诅咒问题,同时基于近似线性相关性分析的在线内核稀疏化方法，进一步的减少了算法的收敛时间。仿真证明,所提算法可以在短时间内收敛,实现了快速规避外部未知干扰源的干扰,减少了接入被干扰频点的次数,并在外部干扰源干扰图样发生变化时,重新对外部干扰源进行学习,相较于传统的基于Q学习的抗干扰频点分配算法拥有好的性能。所提算法无需大量训练,可以通过不断与未知环境进行交互,学习干扰源干扰模式,在线实时做出相应频点分配决策。论文其余部分安排如下:第1节介绍了雷达通信一体化的系统模型并构建了目标问题,第2节介绍了基于传统强化学习的抗干扰频点分配算法和基于核函数强化学习的抗干扰频谱协同算法,第3节和第4节分别给出了仿真分析以及全文总结。

1 问题提出和系统模型建立

本节将对系统模型进行介绍。如图1所示,考虑一个包含通信用频设备和雷达用频设备的雷达通信一体化系统。其中，通信用频设备和雷达用频设备的总设备对数为K,在上述系统中的雷达用频设备为捷变频雷达,用频设备可以对可用频点进行感知,来获得用频设备可用频段的频谱态势[22-23]。

图1 存在外部干扰的雷达通信一体化系统Fig.1 Integrated radar communication system with external interference

在上述系统模型中,时间划分为等长的时隙,每个时隙的长度用T来表示。在上述雷达通信一体化系统中,共有I个可用频点,用频设备k的可用频段中总共有Ik={I1,I2,…,Ik}个可用频点。而不同的用频设备拥有不同的可用频段,但不同用频设备的可用频段之间可能有重叠的频点,并且各个用频设备k的可用频段内单个频点的带宽Bk={B1,B2,…,Bk}也是不相同的,即不同用频设备的频谱是异构的。同时雷达通信一体化系统中存在U个外部干扰源,干扰源对所有用频设备所在的可用频段进行干扰,干扰图样与相关参数并不会被系统中的用频设备感知到,同一网络中的不同用频设备之间不存在频点间干扰。

雷达用频设备通过频率捷变来避开外部的未知干扰源,捷变频雷达的频率捷变技术主要通过干扰分析与频率选择系统来实现的[24]。雷达信号通常是窄带的、带通的、相位或频率调制的函数,这意味着单个散射体的回波波形y(t)[25]具有如下的形式:

y(t)=A(t)sin[Ωt+θ(t)]

(1)

式中,幅度调制A(t)表示脉冲的包络；Ω为频率；θ(t)为相位调制。接收到的信号被分离到两个通道,其中一个通道称为同相通道(I通道),另一个通道称为正交通道(Q通道)。在经过混频和低通滤波后,式(1)中的回波信号为

y(t)=I(t)+jQ(t)

(2)

捷变频雷达对可用频段内的可用频点进行频谱的实时分析,来获得可用频段的干扰状态,捷变频雷达的干扰分析模块在每个时隙对雷达设备可用频点的幅度进行实时监测,单个可用频点处的信号幅度为

(3)

式中,gk, j,t为t时隙雷达设备k的第j个可用频点的幅度值。通信设备根据信干噪比来判断可用频段的频谱态势,其中信干噪比为

(4)

式中,p表示发射功率;σ2表示噪声,包括高斯白噪声和外部干扰源的干扰:

(5)

用频设备为了增加对本用户可用频段附近频点的感知,在用频设备可用频段的两侧均有一个邻频点,如图2所示。邻频点用于感知可用频段两侧相邻频点的频谱态势,其中频点X为邻频点,邻频点不能被使用该频段的用频设备作为工作频点,频点O为用频设备的可用频点。若不同用频设备的可用频点(O)有重叠,则这些用户被划分为同一个簇,由簇头分配重叠频点的优先使用权,如图3所示。

图2 用频设备的可用频段和邻频点Fig.2 Available frequency band and adjacent frequency point of frequency equipment

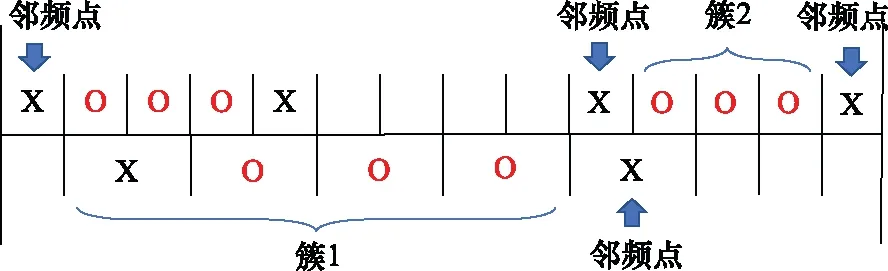
图3 用频设备在可用频段重叠的情况下的分簇情况Fig.3 Clustering of frequency equipment with overlapping available frequency bands

在该系统内,用频设备的频谱池由前y个时隙如图2所示的可用频点和邻频点的频谱态势组成。在t-1时隙用频设备k做出选频决策之后,用频设备对当前时隙的可用频点和邻频点进行感知,获得对应频点的频谱态势集合vk,t-1=(vk,1,t-1,vk,2,t-1,…,vk, j,t-1),其中j为可用频点和邻频点的数目总和。随着用频设备在每个时隙对可用频点和邻频点进行感知,获得t-y时隙到t-1时隙内对应频点的频谱态势,进而构成了用频设备k的频谱池,如图4所示。随着时隙的增加,用频设备不断更新频谱池中的频谱态势,因此在t时隙时,用频设备k可以将本地的频谱池中频谱态势Vk,t=(vk,t-1,vk,t-2,…,vk,t-y)作为算法的输入,对当前时隙下的频点分配进行决策。

图4 频谱池的构建Fig.4 Construction of spectrum pool

由于雷达通信一体化系统中存在未知外部干扰源,因此用频设备所在的无线网络环境是未知的和动态的。这导致用频设备无法从外部环境和频谱态势中直接获得可接入的频点。强化学习提供了一种方法来解决未知动态环境中复杂的决策问题,因此强化学习在抗干扰领域展现出强大的学习能力,这是由于用频设备可以根据过去的经验,对干扰源的干扰规律进行学习,不断更新用频设备的选频策略以最大化长期累计收益,使簇内用频设备可以在每时隙接入频点前,根据当前的频谱池中的频谱态势进行频点选择,从而实现用频设备抗干扰的频点选择策略。由于用频设备可以从过去的频谱态势中获得外部干扰源的干扰策略,因此可以将用频设备的频点选择问题建模为马尔可夫决策过程(Markov decision process, MDP)。

一个马尔可夫决策问题可以由集合{S,A,R,P}来表示,其中S代表状态空间,A代表动作空间,R代表瞬时回报,P代表状态转移概率。接下来介绍有关用频设备k的状态空间,动作空间,瞬时回报以及状态转移概率。

(1) 状态空间:由于干扰源复杂的干扰动作可能与过去y个时隙长度的频谱态势有关,因此用频设备k的状态为sk,t=(vk,1,t-1,vk,2,t-1,…,vk, j,t-1,vk,1,t-2,vk,2,t-2,…,vk, j,t-2,vk,1,t-y,vk,2,t-y,…,vk, j,t-y),其中sk,t为t-1时隙到t-y时隙用频设备k所在频段的历史频谱态势,因此sk,t为一个包含时域和频域频谱态势信息的j×y的二维矩阵。状态sk,t包括用频设备k的可用频点的频谱态势和两侧邻频点的频谱态势;t时隙用频设备k的第j个频点的频谱态势定义为vk, j,t,若感知到该频点受到干扰,则vk, j,t=1,若感知到该频点未受到干扰,则vk, j,t=0。

(2) 动作空间:用频设备k在t时隙的动作为ak,t=(ak,2,t,ak,3,t,…,ak, j-1,t),其中第j-1个元素ak, j-1,t定义为一布尔型变量以表示用频设备k是否接入第j-1个频点,如果用频设备k接入第j-1个频点,则ak, j-1,t=1,否则ak, j-1,t=0。由于用频设备k的可用频点两侧各存在一个邻频点,因此用频设备k的可选频点范围为[2,j-1]。

(3) 瞬时回报:用频设备k的瞬时回报rk,t可以定义为t时隙用频设备k是否接入未被干扰的频点;在t时隙开始时,用频设备k接入频点,之后用频设备感知该时隙可用频点和邻频点的频谱态势,判断用频设备k是否成功接入未被干扰的频点。雷达设备根据幅度值来获得该频点的频谱态势,若gk, j,t≤gt h,则该频点未被干扰,反之gk, j,t≥gt h,则该频点被干扰,其中gt h为被干扰门限[24]。通信用频设备根据接收设备处是否能成功译码来判定用频设备是否接入未被干扰的频点。若用频设备k接入频谱态势为vk, j,t=0的频点,则rk,t=r1,用频设备k接入频谱态势为vk, j,t=1的频点,则rk,t=r2,其中r1和r2分别为用频设备k成功接入未被干扰的频点和未成功接入未被干扰的频点的回报参数。

(4) 状态转移概率:当用频设备k在t时隙的状态sk,t下选取动作ak,t后获得瞬时回报rk,t,状态也由t时隙的sk,t转移为t+1时隙的状态sk,t+1,这个状态转移过程可以被条件概率P(sk,t+1,rk,t|sk,t,ak,t)所表示。用频设备k所在的环境是动态未知的,因此用频设备k不具有状态转移概率P(sk,t+1,rk,t|sk,t,ak,t)的先验信息,而状态转移概率仅与外部环境有关。

在存在外部干扰的复杂电磁环境下,雷达通信一体化通信系统中用频设备k旨在最大化累积折扣回报的期望,即最大化累积折扣用频设备k接入未被干扰的频点次数的期望:

(6)

式中,R为累积折扣回报的期望;λ为折扣系数。t时隙时,用频设备k基于策略π来进行动作ak,t的选择,其中策略π是一个从状态空间S到动作空间A的映射,可以表示为π:sk,t∈S→ak,t∈A。因此,用频设备k的目标为寻找满足下述方程的最优策略π*:

(7)

式中,Eπ(·)为对策略π的期望;Rπ为策略π下的累积折扣回报的期望。

2 基于强化学习的抗干扰频点分配算法

2.1 基于Q学习的抗干扰频点分配算法

在本节中,首先介绍基于Q学习的抗干扰频点分配算法,使用Q学习在未知动态的系统中获得最佳的频点分配策略,以最大化累积折扣瞬时回报的期望。

当用频设备在给定的状态-动作对的情况下根据策略选取相应的动作,状态-动作值(Q值)被定义为累积折扣瞬时回报的期望。因此,在Q学习中的Q值为

(8)

将目标问题建模为马尔可夫决策过程,而马尔可夫决策过程的Q值满足以下的bellman方程:

Qπ(sk,t,ak,t)=Eπ[r(sk,t,ak,t)+

(9)

式中,Eπ(·)是关于状态转移概率P(sk,t+1,rk,t|sk,t,ak,t)的期望。最优的Q值为

(10)

当得到了最优的Q值后,最优的策略为

(11)

也就是在最优策略下选取的动作是为了最大化长期累积的回报。

为了避免陷入局部最优,用频设备使用贪婪算法来选择t时隙的动作ak,t,由于基于贪婪算法的动作选择策略会出现重复选择被干扰频点的问题,因此对贪婪算法进行了如下的改进。若状态动作对(s,a)在之前的时隙被访问,则将状态动作(s,a)添加到集合M中,即(s,a)∈M。在t时隙时,用频设备以概率1-ε随机选取一个动作ak,t,若(sk,t,ak,t)∉M,则用频设备选择随机动作作为本时隙接入的频点,若(sk,t,ak,t)∈M,则根据Q表选取当前状态sk,t下,选择Q值最大的动作作为本时隙接入的频点。或者用频设备以概率ε根据Q表选取当前状态sk,t下,Q值最大的动作作为本时隙接入的频点。动作ak,t的选取如下:

(12)

同时,若用频设备k所在簇内存在两个及以上的用频设备时(即不同用频设备的可用频点有重合),簇内的簇头将优先为雷达用频设备分配频点。

用频设备k在t时隙接入动作ak,t选择的频点后,根据当前时隙的可用频点的频谱态势(vk,1,t,…,vk, j,t),判断当前时隙用频设备k是否成功接入未被干扰的频点,即用频设备k的瞬时回报rk,t。之后用频设备k在t+1时隙对本地的Q表进行更新,更新公式为

Qk,t+1(sk,t,ak,t)=(1-α)Qk,t(sk,t,ak,t)+

(13)

式中,t+1时隙用频设备k的状态sk,t+1=(vk,1,t,vk,2,t,…,vk, j,t,vk,1,t-1,vk,2,t-1,…,vk, j,t-1,vk,1,t+1-y,vk,2,t+1-y,…,vk, j,t+1-y);α为学习速率;λ为折扣系数。用频设备通过不断的训练来得到最优的策略,基于Q学习的抗干扰频点分配算法流程如下所示。

算法1基于Q学习的抗干扰频点分配算法输入:表Qk,t(s,a),用频设备数目K和时隙t;对任意用户k=1,2,…,K执行:步骤 1 用频设备根据改进的贪婪算法选择本时隙的动作ak,t;步骤 2 用频设备k在接入选择的频点后,感知可用频段并获得当前时隙的频谱态势,之后获得回报rk,t;步骤 3 t+1时隙用频设备k根据式(13)对本地Q表进行更新输出:动作ak,t和Q表Qk,t+1(s,a)。

2.2 基于核函数强化学习的抗干扰雷达-通信频谱协同算法

在第2.1节中介绍了基于Q学习的抗干扰频点分配算法,该算法通过找到最优策略来最大化长期折扣回报。大多数情况下,用频设备的状态空间和动作空间的维度随可用频点数呈指数型增长,基于Q学习的抗干扰频点分配算法在面对上述问题时会陷入维度诅咒从而导致收敛时间过长等问题。

因此,当用频设备的可用频点数较大时,用频设备的状态空间和动作空间的维度过大,导致算法难以收敛。为了避免上述问题,在本节中使用基于核函数的方法来解决。使用非参数线性近似对状态-动作值函数进行建模:

Qk,t(sk,t,ak,t)=

(14)

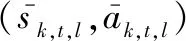
(15)

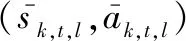
同样的,为了避免陷入局部最优,用频设备使用第2.1节所述的贪婪算法来选择t时隙的动作ak,t。在t时隙时,用频设备以概率1-ε随机选取一个动作ak,t,若(sk,t,ak,t)∉M,则用频设备选择随机动作作为本时隙接入的频点,若(sk,t,ak,t)∈M,则根据字典Dk,t选取当前状态sk,t下,Q值最大的动作作为本时隙接入的频点。或者用频设备以概率ε根据字典Dk,t选取当前状态sk,t下,Q值最大的动作作为本时隙接入的频点。动作ak,t的选取如下:

(16)

(17)

若用频设备k所在簇内存在两个及以上的用频设备时(即不同用频设备的可用频点有重合),簇内的簇头将优先为雷达用频设备分配频点。

同样的,用频设备k在t时隙接入动作ak,t选择的频点后,感知当前时隙的可用频点的频谱态势(vk,1,t,vk,2,t,…,vk, j,t),判断当前时隙用频设备k是否成功接入未被干扰的频点,即用频设备k的瞬时回报rk,t,之后用频设备k更新本地字典Dk,t。字典Dk,t的更新分为两部分,即更新字典中存储的特征对应的权重系数和判断当前特征是否需要加入字典。

在用频设备k获得的当前时隙的可用频点的频谱态势(vk,1,t,vk,2,t,…,vk, j,t)和瞬时回报rk,t后,用频设备对字典中对应特征的权重系数进行更新如下:

(18)

式中,αk,t=[αk,t,l];αk,t+1=[αk,t+1,l];λ为折扣系数;γ为学习速率。

由于使用非参数线性近似对状态-动作值函数进行建模,如式(14)所示,字典Dk,t中的特征数目随着时间的增加而增加,增加了算法计算的复杂度。因此,在不丢失重要信息的情况下控制字典Dk,t中的特征数目是至关重要的。在本节中使用了基于近似线性相关性(approximate linear dependence,ALD)分析的在线内核稀疏化方法[26],用于用频设备k判断t时隙的数据样本的特征(sk,t,ak,t)是否需要加入字典Dk,t。

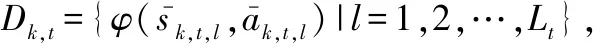
(19)

式中,α=[αk,t,l];μ为确定近似精度的参数。因此,合适的μ值可以在合理的近似精度范围内,确保基于核函数抗干扰频点分配算法的稀疏性。在内核矩阵

被定义之后,式(19)中的δt[27]为

δt=k((sk,t,i,ak,t,i),(sk,t,i,ak,t,i))-

(20)

因此,可以将δt与预设的精度阈值μ进行比较来更新字典,若δt≤μ,则字典不变,否则,将数据样本特征添加到字典中。基于ALD的在线稀疏化方法的流程如下所示。

算法 2 基于ALD的在线稀疏化方法输入;数据样本特征(sk,t,ak,t),字典Dk,t和近似精度阈值μ; 计算δt: δt=k((sk,t,i,ak,t,i),(sk,t,i,ak,t,i))- kTk,t(sk,t,i,ak,t,i)Kk,tkk,t(sk,t,i,ak,t,i) if δt≤μ: Dk,t+1=Dk,t; else Dk,t+1=Dk,t ∪ (sk,t,ak,t);输出:字典Dk,t+1。

通过上述的基于ALD的在线内核稀疏化方法,可以大幅降低基于核函数算法的计算复杂度和字典存储成本,提高算法性能。

用频设备在每个时隙t开始时分配一个频点,不同用频设备使用不同频点。同时,用频设备开始学习外部干扰源的干扰规律,至用频设备处的频点分配算法收敛;若在算法收敛之后,当前频段干扰发生变化用频设备继续按照之前的频点分配策略选择频点,进而用频设备得到接入被干扰的频点时的瞬时回报,这时启动频点分配算法重新进行学习,至用频设备处的频点分配算法重新收敛。基于核函数强化学习的抗干扰雷达-通信频谱协同算法的流程如下所示。

算法 3 基于核函数强化学习的抗干扰雷达通信频谱协同算法输入:字典Dk,t,权重系数αk,t,时隙t和用频设备数目K;步骤 1 对任意用户k=1,2,…,K执行:步骤 1.1 用频设备根据改进的贪婪算法选择本时隙的动作ak,t;步骤 1.2 用频设备k在接入选择的频点后,感知可用频段并获得当前时隙的频谱态势,之后获得回报rk,t;步骤 1.3 根据下式对字典Dk,t中存储特征的权重系数进行更新: αk,t+1=αk,t+γ(λmaxa{αTk,tk(sk,t+1,a)} -αTk,tk(sk,t,ak,t)+rk,t)k(sk,t,ak,t)步骤 2 用频设备k基于ALD的在线稀疏化方法对字典进行更新;输出:动作ak,t,字典Dk,t+1和权重系数αk,t+1。

3 仿真结果与分析

在本节中,通过仿真测试的方式,将提出的基于核函数强化学习的抗干扰雷达-通信频谱协同算法与传统的基于Q学习的抗干扰频点分配算法进行对比评估。

基于第2节建立的系统模型,设定存在外部干扰的雷达通信一体化系统中共有K=5个用频设备,用频设备包括4个通信用频设备和1个雷达用频设备,第k=3个用频设备为雷达用频设备;雷达通信一体化系统中共有I=35个可用频点,每个可用频点带宽为1 MHz,各个用频设备可用频段中可用频点的数量为I5={4,6,6,4,4},其中雷达用频设备(k=3)和通信用频设备(k=2)之间的可用频段存在重叠的部分,而其他用频设备的可用频段之间不存在重叠的部分;各个用频设备可用频段内单个频点的带宽Bk={1 MHz, 1 MHz, 2 MHz, 1 MHz, 1 MHz},即用频设备3的可用带宽为12 MHz,其中包括6个带宽为2 MHz的可用频点。对于上述系统模型,可以得到各个用频设备的可用频段以及邻频点起始的频点号为{1, 7, 11, 25, 30}。同时,用频设备2的3个可用频点和1个邻频点与用频设备3的1个可用频点和1个邻频点重叠,如图5所示。噪声功率谱密度为-103 dBm,通信用频设备接收端噪声功率与信号功率的比值为1.5,单个时隙长度为T=0.1 s。

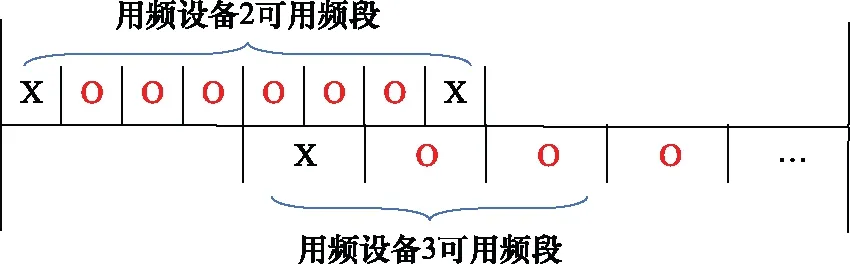
图5 可用频段示意图Fig.5 Diagram of available frequency band

雷达通信一体化系统中存在U=1个对用频设备未知的外部干扰源,外部干扰源对所有可用频点进行扫频干扰,干扰图样1和干扰图样2如图6和图7所示。基于核函数强化学习算法的相关参数如表1所示。

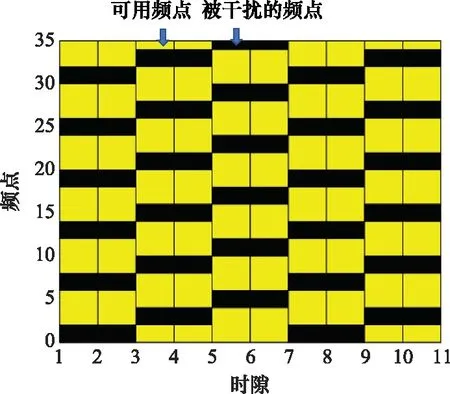
图6 干扰图样1Fig.6 Interference pattern 1

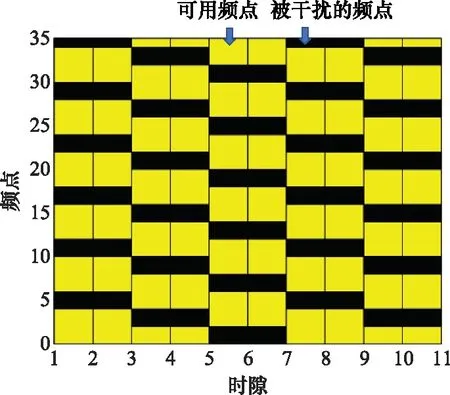
图7 干扰图样2Fig.7 Interference pattern 2

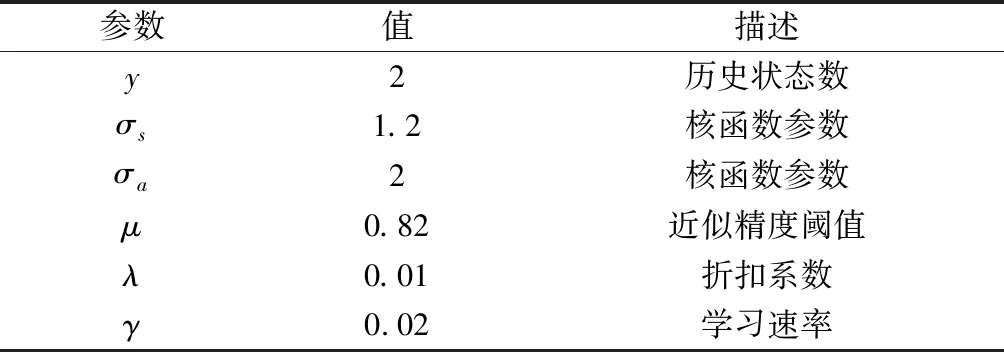
表1 参数列表

首先，将所提出的基于核函数强化学习的抗干扰雷达-通信频谱协同算法与传统的基于Q学习的抗干扰频点分配算法进行性能对比。图8为基于不同算法的用频设备每个时隙接入被干扰的频点的次数。从图8(a)可以看出,在第25个时隙附近用频设备可以完全避开外部干扰。从图8(b)可以看出,在第180个时隙附近用频设备可以完全避开外部干扰。因此,在上述所述的仿真场景中,所提算法通过学习可以更快地避开外部干扰,接入未被干扰的频点。

图8 用频设备接入被干扰的频点的次数Fig.8 Number of times the frequency equipment is connected to the interfered frequency point

之后对所提出算法和基于Q学习算法收敛情况进行了分析对比,如图9～图13所示,分别为基于两种算法的用频设备1～用频设备5的收敛情况。可以看出,所提出算法可以在20个时隙左右收敛,基于Q学习算法在400个时隙左右收敛,因此所提算法较基于Q学习算法可以在更短的时间内收敛至稳定。

图9 用频设备1基于两种算法的收敛情况Fig.9 Convergence of the two algorithms for frequency equipment 1

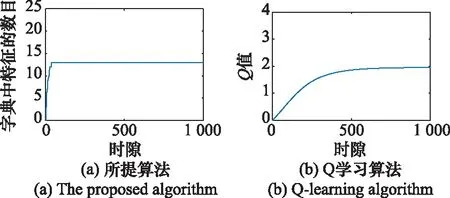
图10 用频设备2基于两种算法的收敛情况Fig.10 Convergence of frequency equipment 2 based on two algorithms

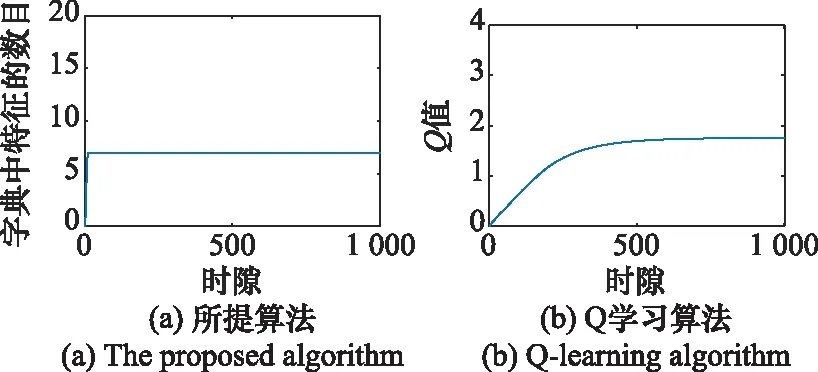
图11 用频设备3基于两种算法的收敛情况Fig.11 Convergence of frequency equipment 3 based on two algorithms

图12 用频设备4基于两种算法的收敛情况Fig.12 Convergence of frequency equipment 4 based on two algorithms

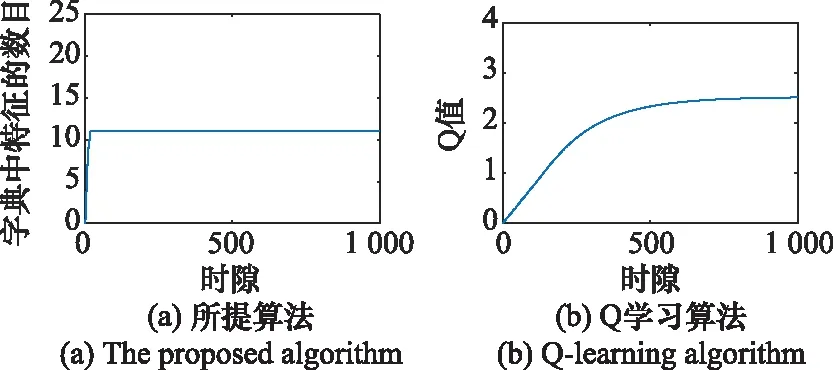
图13 用频设备5基于两种算法的收敛情况Fig.13 Convergence of frequency equipment 5 based on two algorithms

图14和图15对基于核函数强化学习的抗干扰雷达-通信频谱协同算法每时隙频点接入情况进行了分析。从图14中可以看出,在最初的是10时隙中,用频设备存在接入被干扰的频点的情况;而从图15中可以看出,当所提出的算法收敛后,可以在每个时隙避开外部的恶意干扰,并接入未被干扰的频点。最后,对所提算法在存在不同干扰图样的情况下进行仿真分析。在前600个时隙内,外部干扰源选择如图6所示的干扰图样1对可用频段进行干扰,在第600个时隙时外部干扰源更换干扰图样,根据如图7所示的干扰图样2对可用频段进行干扰。

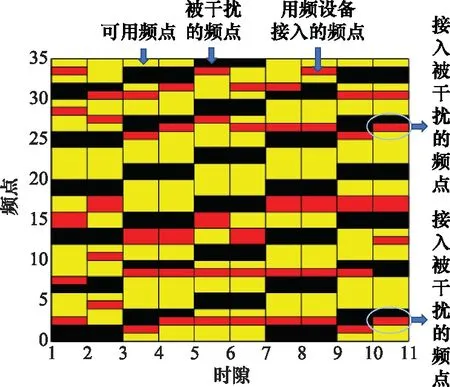
图14 所提算法收敛前每时隙频点接入情况Fig.14 Frequency access per slot before convergence of the proposed algorithm

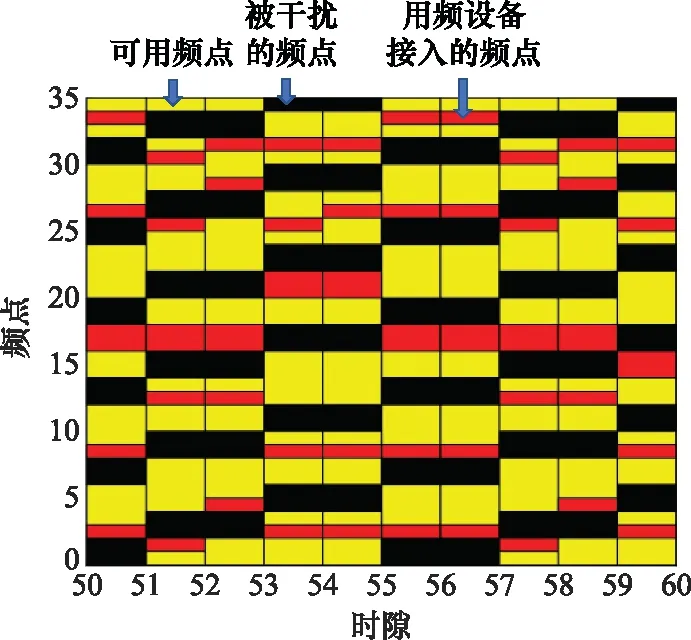
图15 所提算法收敛后每时隙频点接入情况Fig.15 Frequency access per slot after convergence of the proposed algorithm

图16和图17对基于核函数强化学习的抗干扰雷达-通信频谱协同算法在干扰图样变化前后每时隙频点接入情况进行了分析。从图16和图17中可以看出,在外部干扰发生变化的前后,用频设备均可以接入未被干扰的频点。图18为基于所提出算法的用频设备每个时隙接入被干扰的频点的次数。由图16和图17可知,外部干扰源在第600个时隙的干扰模式由干扰图样1变更为干扰图样2,因此从图18中可以看出,在干扰模式变换后用频设备重新对干扰图样进行学习,并且所提出的算法可以快速收敛,因此用频设备可以快速避开外部干扰,接入未被干扰的频点。

图16 所提算法在干扰变化前每时隙频点接入情况Fig.16 Frequency point access of each time slot before interference changes in the proposed algorithm

图17 所提算法在干扰变化后每时隙频点接入情况Fig.17 Frequency point access of each time slot after interference changes in the proposed algorithm

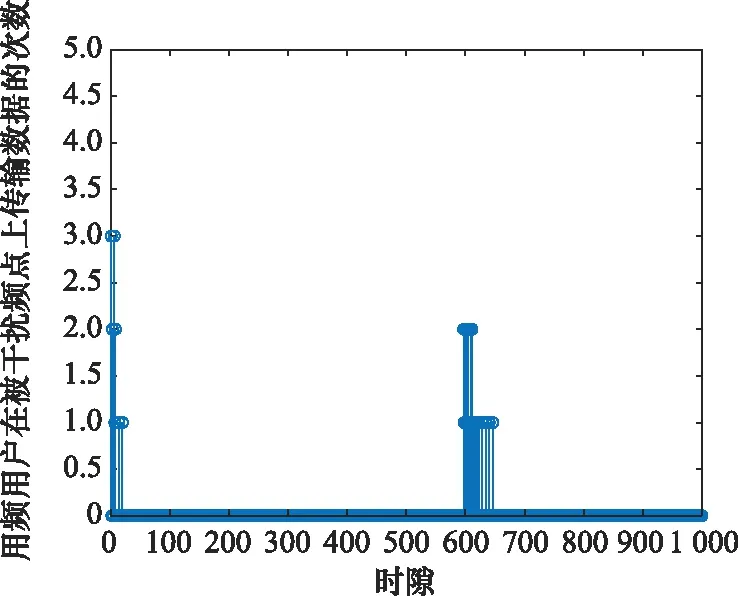
图18 用频设备接入被干扰频点的次数Fig.18 Number of times for the user accesses the interfered frequency point

4 结 论

针对存在未知干扰源的系统,对雷达通信一体化系统的抗干扰频谱协作问题进行探索与研究,旨在最大化用频设备接入未被干扰频点的期望。通过与基于Q学习的抗干扰频点分配算法的仿真结果进行对比,所提算法通过基于核函数的方法和基于近似线性相关性分析的在线内核稀疏化方法,共同降低了所提算法的收敛时间,同时避免出现维度诅咒等问题。所提算法可以在较短时间内收敛,同时快速规避外部未知干扰源的干扰,并在外部干扰源干扰图样发生变化时,重新对外部干扰源进行学习。所提算法实现了在干扰源未知的情况下,用频设备对外部干扰的规避和干扰规律的学习。