空域色噪声背景下双基地MIMO雷达角度估计

师俊朋, 文方青, 艾 林, 张 弓, 龚政辉

(1. 国防科技大学电子科学与工程学院, 湖南 长沙 410073;2. 三峡大学计算机与信息学院, 湖北 宜昌 443002;3. 长江大学电子信息学院, 湖北 荆州 434200;4. 南京航空航天大学电子信息工程学院, 江苏 南京 210016)

0 引 言

多输入多输出(multiple input multiple output,MIMO)雷达技术是下一代阵列雷达系统最具潜力的发展方向之一,也是学术界和工程界的研究热点[1]。该研究方向不仅有重大的理论和学术意义,而且具有巨大军用价值和潜在的民用价值,其在国防、反恐与救援、遥感、交通运输诸多领域应用前景广阔。所谓MIMO雷达,即指雷达系统采用多根发射天线和多根接收天线的配置,且发射天线发射相互正交的波形。由于MIMO雷达采用波形分集和空间分集,能形成一个远大于实际物理孔径的阵列虚拟孔径。相比相控阵雷达,MIMO雷达具备更好的反隐身、抗截获、抗干扰等性能。一般而言,MIMO雷达可分为两大类:分布式MIMO雷达和集中式MIMO雷达[2-3]。分布式MIMO雷达采用空间广泛分布的收发阵元,能有效应对目标雷达截面(radar cross section,RCS)系数闪烁现象。集中式MIMO雷达采用共址天线,能够获得高分辨率的目标方位估计。本文主要关注双基地MIMO雷达中角度估计问题,属于集中式MIMO雷达范畴。

联合波离角(direction of departure, DOD)和波达角(direction of arrival, DOA)估计是双基地MIMO雷达目标定位的基本任务[4-6]。经过十余年的发展,己涌现一大批性能优异的角度估计算法。典型的估计策略有谱峰搜索类算法[7],基于旋转不变技术的信号参数估计(estimating signal parameter via rotational invariance techniques, ESPRIT)类算法[8],稀疏表示类算法[9],张量分析类算法[10-11],其中,张量算法由于利用MIMO雷达数据的多维结构特性,因而往往能获得更精确的参数估计性能。然而,上述算法良好的估计性能均是在理想高斯白噪声的假设下获得的。在实际工程中,由于雷达系统的复杂性、任务的多样性及探测背景的特殊性,MIMO雷达的接收噪声往往是非高斯的。其中,空域色噪声是MIMO雷达中一类典型的非白高斯噪声,在诸多场景中均会涉及。例如,考虑到赋予MIMO雷达发射波束一定的指向性(MIMO-相控阵雷达)[12],以及在一体化MIMO雷达-通信系统中[13],均需要发射非正交的波形,而非正交发射波形会导致空域有色噪声[14]。空域色噪声会导致噪声协方差矩阵不再与单位矩阵呈比例关系,因而引起现有矩阵与张量分解算法性能恶化,甚至失效。

针对MIMO雷达中的空域色噪声问题,目前己有一些抑噪算法。概括说来,主要有空域互协方差算法[15-18]、时域互协方差法[19-21]、协方差差分法[22-23]、高阶累积量法[24]、矩阵填充法[25-26]。其中,空域互协方差法将发射阵列划分为若干个子阵列。尽管阵列接收噪声是空域相关的,但噪声经过不同的匹配滤波器后会不相关,因此不同发射子阵列所对应的匹配滤波输出的噪声互协方差为0。然而,该方案会减小MIMO雷达的虚拟孔径,因而在高信噪比(signal to noise ratio, SNR)时参数估计的精度会下降;时域互协方差法将阵列匹配滤波输出在时域上划分成若干个子阵列,其假设不同脉冲间的噪声是非相关的,通过噪声时域互相关特性抑制色噪声。该方案没有孔径损失,但是其需要噪声及目标RCS满足某些特殊的要求;高阶累积量法利用色噪声的高阶(如4阶)累积量消除色噪声的影响,但该方案要求目标的RCS系数服从严格的非高斯分布,且算法的复杂度往往较高;协方差差分法主要利用平稳色噪声协方差矩阵的Toeplitz特性,通过构造差分变换矩阵抑制色噪声。该方案也不存在孔径损失,但其可辨识性会下降,且角度估计需要额外的解模糊运算;考虑到色噪声协方差矩阵的稀疏特性,文献[25-26]提出基于矩阵填充的色噪声抑制框架,该方法对噪声或者目标RCS无特殊要求,且不存在虚拟孔径损失。该框架通过去除信号协方差矩阵中受色噪声影响的数据抑制有色噪声,将无噪协方差矩阵的恢复问题等效为矩阵填充问题,最后采用ESPRIT算法进行角度估计。其中,文献[25]利用凸优化工具箱(如CVX)进行矩阵填充,文献[26]采用奇异值阈值 (singular value thresholding, SVT)算法对MIMO雷达无噪协方差矩阵进行恢复[27]。然而,凸优化工具箱算法一般以内点法为基础,其运算效率往往低下，而SVT对相关参数的设置较敏感，算法鲁棒性较差。此外，上述算法中MIMO雷达数据的多维结构特性被忽略，参数估计的精度还有较大的提升空间。

一般来说，矢量是一个一维张量，矩阵是一个二维数组，而高于二维的数组被统称为张量。相比矢量和矩阵分析,张量分析方法能充分利用数据内部的结构信息,因而能获得更加精确的结果。由于MIMO雷达数据具有丰富的空-时张量结构,故使用张量分析可有效提高参数估计精度[10-11]。特别是在色噪声背景下,使用张量分解技术能获得更加精确的角度估计性能[17,21]。受启发于张量填充思想[28],本文提出一种张量框架下改进的双基地MIMO雷达色噪声抑制方法。该方法首先构造MIMO雷达匹配滤波后的协方差张量信号模型,并通过去除协方差张量中受噪声协方差中非零元素影响的元素对色噪声进行抑制。然后，通过张量框架下的快速填充算法对无噪的协方差张量进行恢复。最后,利用平行因子(parallel factor,PARAFAC)分解获得含DOD和DOA的因子矩阵,再通过最小二乘算法对DOD和DOA进行拟合。所提算法能充分利用MIMO雷达数据的张量结构,且对参数设置不敏感。相比现有算法,所提算法具有更高的估计精度和更好的鲁棒性,仿真结果验证了该方法的有效性。

1 张量基础与信号模型

1.1 张量基础

一个张量就是一个多维数组。本文将所涉及的张量基础表述如下。

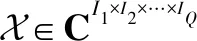
(1)

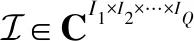
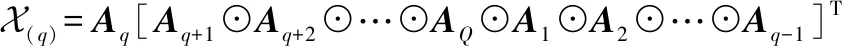
(2)

式中,⊙为Khatri-Rao积。

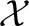
(3)

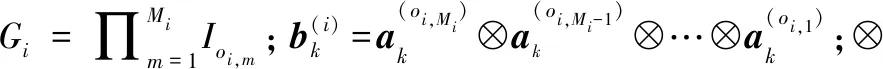
1.2 信号模型

(4)

式中,bk(τ)为目标的RCS,并假设其在一个脉冲持续时间Tp内保持不变;τ为慢时间索引;at(φk)为第k的目标的发射响应矢量,s(t)=[s1(t),s2(t),…,sM(t)]T为发射波形矢量。阵列接收信号可表示为

(5)

其中,ar(θk)=[1,e-jπ sin θk,…,e-jπ(N-1)sin θk]T为第k的目标的接收响应矢量;w(t,τ)=[w1(t,τ),w2(t,τ),…,wN(t,τ)]T为阵列接收噪声,本文假设噪声满足均值为零、协方差为C的色高斯分布,即

E{w(t1,τ)wH(t2,τ)}=Cδ(t1-t2)

(6)

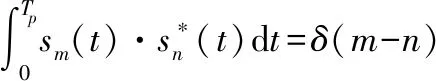
(7)

则

[At⊙Ar]b(τ)+n(τ)=Ab(τ)+n(τ)

(8)

Ry=E{y(τ)yH(τ)}=Rs+Rn

(9)

其中,Rs=ARbAH为信号协方差矩阵,Rb=E{b(τ)bH(τ)}。本文假设目标RCS是非相关的,则Rb为一个对角矩阵,Rn=E{n(τ)nH(τ)}为噪声协方差矩阵。事实上,Ry也可以表示成张量[17]的形式:

(10)

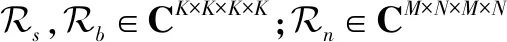
如果MIMO雷达的一个相干处理时间内包含L个脉冲,即τ=τ1,τ2,…,τL,则阵列协方差矩阵可以通过

(11)

2 所提算法

2.1 色噪声抑制

首先分析色噪声对噪声协方差矩阵的具体影响。根据nm(τ)的具体形式,易知

(12)

将式(12)代入Rn,并利用性质(A⊗B)·(C⊗D)=(AC)⊗(BD),可得

wH(t2,τ)]H}dt1dt2=I⊗C

(13)

式中,I为单位矩阵。当阵列接收噪声为空域白噪声时,假设噪声功率为σ2,则阵列接收噪声为C=σ2I,此时Rn=σ2I。因此可知,白噪声是色噪声的一种特殊情况。由于单位矩阵不会影响信号特征分布,因而传统子空间分解算法在高斯白噪声的条件下有效。然而,在色噪声的影响下,噪声协方差矩阵不再与单位矩阵呈比例,因而子空间算法会失效。

定义Ω为Rn中非零元素的索引集合,即

Ω={(m,n)∣Rn(m,n)≠0}

(14)

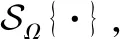
(15)

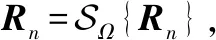
(16)

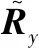
(17)

式中,rank{R}表示R的秩。由于矩阵的秩是非凸的,因而上述优化是一个非确定性多项式问题。一种有效的凸松弛方法是利用矩阵的核范数约束替换上述对秩的约束,从而将上述优化问题变为

(18)

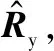
(19)

上述问题可通过凸优化工具箱如CVX或SeDuMi求解,也可以利用矩阵填充算法求解,如SVT。然而,凸优化工具箱大多基于内点法,其计算复杂度往往非常高。SVT算法计算效率高,但其对参数的设置较为敏感。此外,由于上述优化过程忽略了MIMO雷达数据的多维结构特性,因而数据恢复效果在低SNR条件下性能较差。

2.2 张量填充

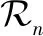
(20)

并考虑通过类似于式(18)的优化过程恢复无噪信号协方差张量,即

(21)

上述张量的核范数定义为张量的模-n展开的加权和,即

(22)

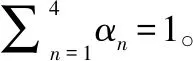
(23)

上述问题是一个不可微分的凸优化问题,该问题可借助于变量分离技术进行求解。为加快算法运算速率,文献[28]提出通过平滑上述优化问题进行求解,其优化目标函数为

(24)

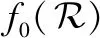
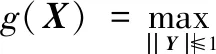
(25)

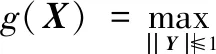
(26)

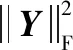
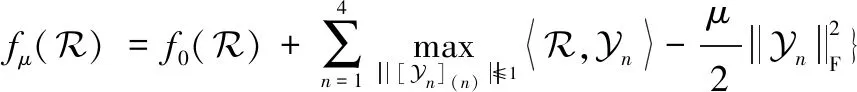
(27)

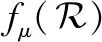
(28)

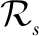
2.3 PARAFAC分解

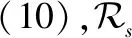
(29)

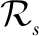
(30)

(31)

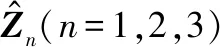
(32)

对于上述优化问题,一般采用交替最小二乘法。假设At,Ar和Ac中的任意二者已知,则可通过最小二乘完成对未知矩阵的估计,对At,Ar和Ac的最小二乘估计分别为

(33)

其中,(·)†表示矩阵伪逆。对At,Ar和Ac的更新采用交替迭代的方式进行,直到算法收敛。由于交替最小二乘算法对初值敏感,本文采用COMFAC算法加速算法收敛。首先将三阶PARAFAC模型进行压缩,然后再对压缩后的低维张量进行算法迭代,最后再将获得的解恢复到原始高维张量空间。

由PARAFAC分解的过程可知,张量分解实际上是利用矩阵分解进行的。但是传统矩阵分解方法都是张量在某个维度展开的基础上进行的,其只能利用张量数据某个维度的结构而忽略了张量数据其他维度的结构。使用张量分解方法具有天然张量增益[29],能够充分利用数据的多维结构,从而获得更加精确的分解结果。

2.4 联合DOD和DOA估计

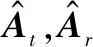
kAt+kAr+kAc≥2K+2

(34)

时,上述PARAFAC分解除了具有列模糊和尺度模糊,其具备唯一性。其中,kA表示A的Kruskal秩。列模糊和尺度模糊可以表示为

(35)

其中,Π是一个置换矩阵;Δ1,Δ2和Δ3为分别为对应的尺度模糊矩阵,均为对角矩阵,且Δ1Δ2Δ3=I;N1,N2和N3为误差矩阵。

(36)

式中,phase{·}为取相位运算。易知

(37)

令ht,k和ht,k分别是ht,k和hr,k的估计值,则ct,k和cr,k可通过最小二乘法估计如下:

(38)

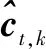
(39)

3 算法分析

3.1 可辨识性

M+N-1.5≥K

(40)

故所提算法最多可辨识M+N-1个目标。传统的ESPRIT算法[8]可辨识min{(M-1)N,M(N-1)}个目标;基于空域互协方差的ESPRIT算法[16](简记为SC-ESPRIT)和基于空域互协方差张量高阶子空间分解[17](简记为SC-HOSVD)的算法最多可辨识min{(M1-1)N,M1(N-1),(M2-1)N,M2(N-1)},其中M1和M2分别为非重叠子阵列中阵元的个数,M1+M2=M;基于时域互协方差张量高阶子空间分解的算法[21](简记为TC-HOSVD)与基于矩阵填充的ESPRIT算法[26](简记为SVT-ESPRIT)的可辨识性与传统ESPRIT相同。相比之下,所提算法的可辨识性可能会弱于这些算法。然而,由于所提算法能够利用阵列信号的张量特性,因而所提算法的精度会优于这些算法,通过仿真结果可证明所提算法性能的优势。

3.2 统计克拉美罗界

假设Rn中含有确定的未知参数q1,q2,…,qP。根据文献[34],色噪声背景下双基地MIMO雷达角度估计的统计克拉美罗界为

(41)

其中,

(42)

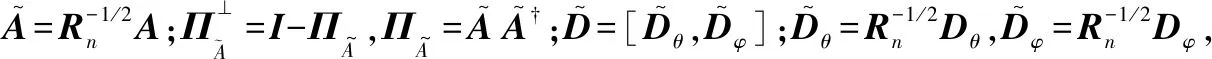
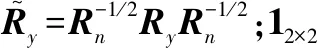
4 仿真结果

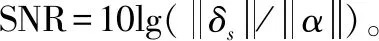
仿真实验1:高斯白噪声背景下不同SNR时的RMSE比较。其中,M=8,N=8,L=500,并将α和β分别设置为0.9和100,此时Rn≈0.9I。仿真结果如图1所示。

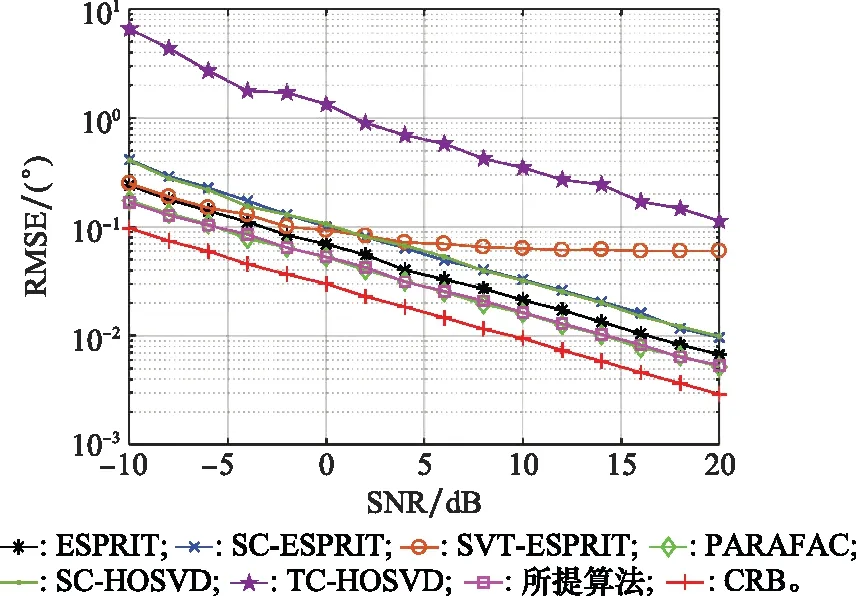
图1 白噪声背景下不同算法的RMSE随SNR变化情况Fig.1 RMSE with SNR of different algorithms in white noise background

从图1可以看出,所有的算法的RMSE都会随着SNR的提高而降低。由于目标特征矢量不满足时域互协方差算法的要求,TC-HOSVD算法性能会大打折扣。由于对参数设置敏感,SVT算法在低SNR下性能几乎与ESPRIT一致,但高SNR下算法性能几乎维持不变。空域互协方差方法(SC-ESPRIT和SC-HOSVD)受孔径损失的影响,性能比传统的ESPRIT差。本文所提算法的性能和传统PARAFAC算法相差不大,相比之下,二者性能均优于ESPRIT算法。

仿真实验2:色噪声背景下不同SNR时的RMSE性能比较。其中,M=8,N=8,L=500,α=0.9,β=0.01,仿真结果如图2所示。

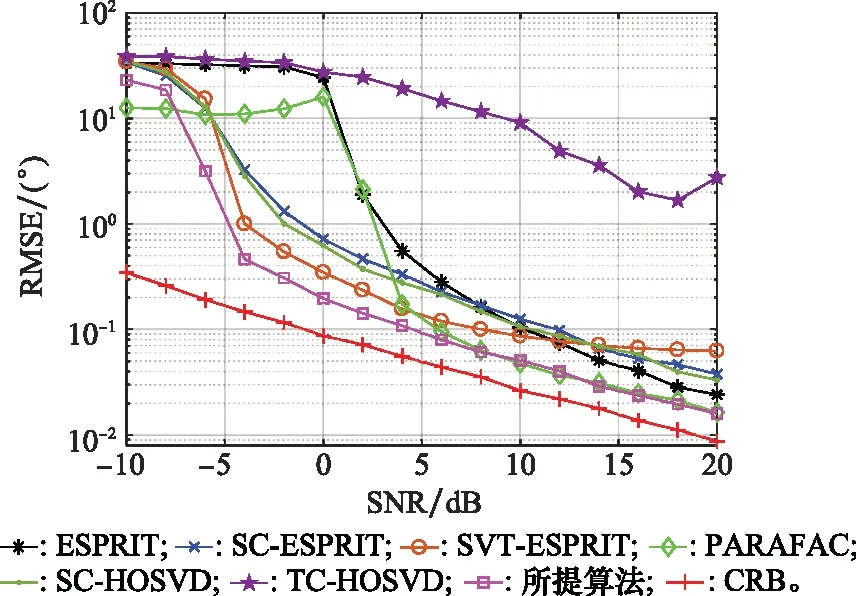
图2 色噪声背景下不同算法的RMSE随SNR变化情况Fig.2 RMSE with SNR of different algorithms in colored noise background

可以看出,在低SNR条件下(SNR≤-5 dB),所有算法性能均不理想。受色噪声的影响,ESPRIT算法在SNR≤0 dB时无法正常工作,但采用了抑噪策略的算法的性能均会随着SNR的増加而改善。由于抑制过程存在孔径损失,SC-ESPRIT算法性能在高SNR条件下弱于ESPRIT算法,但在使用张量分解技术后,SC-HOSVD性能会有所改善。由于TC-HOSVD对回波系数有特殊要求,在本仿真条件下,算法会完全失效。SVT-ESPRIT算法对参数敏感,尽管其在低SNR时具有良好的估计性能,但当SNR较高(SNR≥12 dB)时性能也会比传统的ESPRIT差。相较而言,由于能利用阵列数据的多维结构,所提算法的性能一直处于最优的状态。此外,应该注意到,色噪声对常规算法性能影响主要在低SNR区域,而在高SNR条件下对算法影响影响较小。因而PARAFAC算法在低SNR条件下会失效,而在高SNR时性能趋近所提算法。

仿真实验3:色噪声背景下算法在不同快拍数L条件下的RMSE性能比较。其中,M=8,N=8,SNR=0,α=0.9,β=0.01,仿真结果如图3所示。可以看出,ESPRIT、PARAFAC及TC-HOSVD在此场景下均会失效,而其余算法的性能都会随着L的増加而改善。得益于张量结构的应用,所提算法的性能要优于其他比较算法。

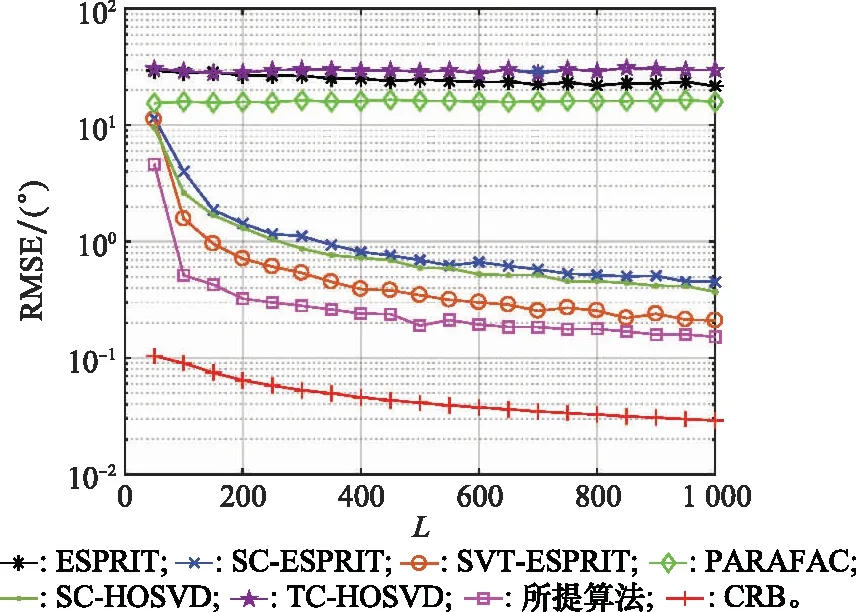
图3 色噪声背景下不同算法的RMSE随快拍数变化情况Fig.3 RMSE with snapshot number of different algorithms in colored noise background

仿真实验4:色噪声参数β对RMSE性能的影响。其中,M=8,N=8,L=500,SNR=0,α=0.9,仿真结果如图4所示。由于当β≫1时,Rn≈αI,即噪声退化为高斯白噪声。而当β<1时,随着β的减小,噪声的空域相关性逐步变大。仿真结果表明,随着β的増加,所有算法的RMSE均会有所改善,但当β>10时,算法的RMSE性能几乎不再变化。另外,使用了抑噪策略的算法(除TC-HOSVD外),其性能均对β不太敏感。尽管SVT-ESPRIT算法也对β不敏感,但其RMSE曲线总和所提算法的RMSE曲线间存在一定的差距。相比较而言,所提算法的性能始终优于所有算法。

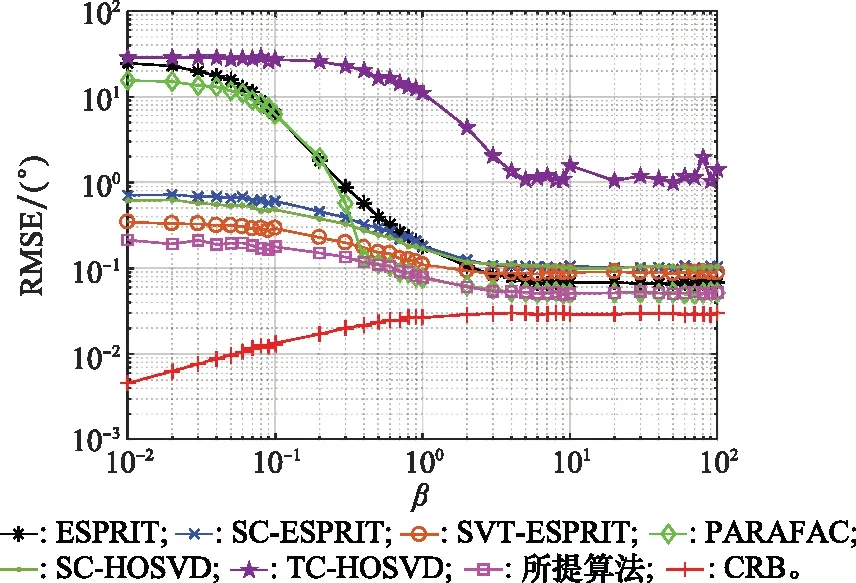
图4 色噪声背景下不同算法的RMSE随噪声参数β变化情况Fig.4 RMSE with noise parameter β of different algorithms in colored noise background

仿真实验5:色噪声背景下发射阵元数M对RMSE性能的影响。仿真结果如图5所示。由仿真结果可知,发射天线数目M越大,算法的RMSE性能越好。从式(13)可以看出,Rn中非零的元素的个数应该是MN2,其占协方差矩阵Rn元素总数(M2N2)的1/M,故M越大,受色噪声影响的协方差数据就越少,从而算法性能越好。从仿真结果可以看到SVT-ESPRIT算法由于对参数敏感,其在M≥10时会失效,而其他算法均能正常运行。此外,所提算法在不同的M时均能够保持最好的估计性能。

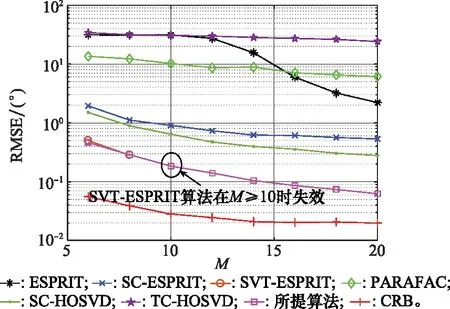
图5 色噪声背景下不同算法的RMSE随阵元数变化情况Fig.5 RMSE with number of array elements of different algorithms in colored noise background

5 结 论

针对双基地MIMO雷达角度估计中的有色噪声问题,本文提出一种基于张量分析的信号处理框架。首先,构造角度估计的协方差张量模型。其次,将色噪声抑制问题转化为一个张量填充问题,并利用现有快速算法进行无噪数据协方差张量的恢复。然后,使用PARAFAC分解对协方差张量进行分解。最后,使用最小二乘技术完成目标DOD和DOA的联合估计。所提算法可有效抑制空域色噪声,不会引起阵列孔径损失。仿真结果表明,所提算法精度高、鲁棒性好。