捷变频联合波形熵的密集假目标干扰抑制算法
2021-05-31全英汇沙明辉刘智星邢孟道
方 文, 全英汇,*, 沙明辉, 刘智星, 高 霞, 邢孟道
(1. 西安电子科技大学电子工程学院, 陕西 西安 710071;2. 北京无线电测量研究所, 北京 100854;3. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引 言
密集假目标干扰对截获的雷达发射信号进行延时叠加或截取叠加后转发,沿距离维在真实目标周围形成多个假目标。由于与雷达发射信号间有良好的相关性,干扰信号同样获得匹配滤波增益,进而导致恒虚警检测器检测门限的提高,使密集假目标干扰具备压制性的效果。此外,通过对干扰信号脉间、帧间时序关系的设计也可在雷达检测端形成大量具备虚假信息的假目标,实现欺骗性的效果[1-3]。可见,密集假目标干扰不仅造成真假目标识别困难,而且严重消耗雷达资源。
为对抗密集假目标干扰,国内外学者从不同角度提出了多种抗干扰算法。在利用目标和干扰在空、时、频和变换域的可分离性方面:文献[4]中分析了干扰机资源有限条件下产生的密集假目标干扰多普勒集中分布在若干个数值的有限邻域内的特点,利用频域的差异抑制干扰信号。文献[5-7]中根据目标和干扰空间角度上的不同,分别采用盲源分离技术和自适应旁瓣对消抗干扰。文献[8]基于机载雷达分析了密集假目标干扰在空时两维的特性,提出一种干扰抑制算法。文献[9]中基于脉间调频斜率捷变雷达,利用分数阶傅里叶变换在分数阶域抑制密集假目标干扰。但是,未来干扰机计算资源和调制能力的改善将使密集假目标干扰的密集度与逼真性提高,进而在空、时、频以及极化域与真实目标回波信号重叠,难以有效分离目标和干扰信号。
在数据处理层面抗干扰方面:针对单部雷达数据处理层面抗干扰,文献[10-14]分别利用真假目标在功率、角度量测上统计特性的差异以及多时刻量测递推融合,实现对密集假目标干扰的识别。若雷达处于强干扰对抗环境中,真实目标无法形成稳定航迹时,上述抗干扰算法可能并不适用。而文献[15-19]利用信息融合技术,研究组网雷达在数据处理层面鉴别密集假目标干扰,分别提出基于同源量测融合、主被动雷达数据融合等不同的抗干扰算法,为后续研究提供了新思路。但亟需解决组网雷达间空时配准的问题,同时实际中也可能存在不具备雷达组网的情况。
此外,文献[20-22]根据目标轨迹在快-慢时间两维平面上为连续直线而干扰为杂乱分布的点这一特征,分别利用Hough变换和形态学滤波抑制干扰。但是对于部分目标回波中存在的干扰旁瓣,并没有进行剔除。当干扰旁瓣能量较强时,会导致相参积累后旁瓣电平抬高,影响目标检测;严重时会使得抗干扰算法失效。
针对这一问题,以自卫式干扰下频率捷变雷达抗密集假目标干扰为背景,在文献[22]的基础上,进一步改进,提出一种捷变频联合波形熵的密集假目标干扰抑制算法。首先,利用Kittler最小误差法计算回波中噪声和真假目标的最佳分割阈值,并进行二值化处理;其次,根据二值化后目标运动轨迹为一条与慢时间维平行的直线而干扰为散乱分布的点这一特性,从波形熵的角度识别目标和干扰;接下来,采用局部离群因子(local outlier factor, LOF)检测算法对目标回波中叠加有较强干扰旁瓣的数据进行剔除,抑制相参处理后的旁瓣;最后,采用稀疏重构算法进行脉间相参处理。数字仿真实验和外场实测数据处理验证了基于波形熵的捷变频雷达抗密集假目标干扰算法的有效性。与文献[22]中基于形态学滤波的密集假目标干扰抑制算法相比,所提算法具有如下优点:
(1) 在一定干信比范围内从目标信息保留的角度来看,本文采用的阈值分割算法,即Kittler算法要优于文献[22]中的Otsu算法。
(2) 在干扰抑制过程中文献[22]所用形态学滤波方法需要调整结构元以匹配目标二值化结果,并且开运算也存在目标信息丢失问题;而本文波形熵方法并不需要设置参数,同时也不存在目标信息丢失问题。
(3) 对于目标回波中叠加有较强干扰旁瓣的数据,文献[22]中并没有进行处理,而本文采用LOF检测算法予以剔除。
(4) 当干扰信号功率较强,即干信比较高时所提算法仍能有效抑制干扰。算法性能对比分析结果表明,当干信比大于34 dB时,文献[22]中抗干扰算法失效;而本文所提抗干扰算法失效的干信比临界点为58 dB。
1 信号模型
1.1 捷变频信号模型
捷变频雷达指在一个相参处理间隔中发射脉冲载频在宽频带范围内的部分频点上随机跳变。第m个发射脉冲信号可以表示为
(1)
式中,

假设雷达观测场景中存在G个运动点目标,不考虑目标加速度,在t=0时刻第g个目标距离为rg,径向速度为vg,第m个脉冲的回波信号可以表示为
(2)
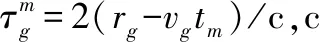
1.2 密集假目标干扰信号模型
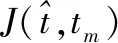
(3)

(4)
式中,
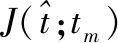
(5)

2 基于波形熵的捷变频雷达抗干扰算法

图1 本文算法流程图Fig.1 Flow chart of the proposed algorithm
2.1 基于Kittler算法的噪声抑制
Kittler最小误差法是一种基于贝叶斯最小分类错误思想的阈值分割算法[23]。本文利用Kittler算法计算回波中真假目标和噪声的最佳分类阈值,并进行0-1二值化处理,以抑制噪声,算法步骤如下。
设脉压后回波数据矩阵为A,矩阵维度为X×Y,矩阵的行下标对应慢时间维,矩阵的列下标对应快时间维,A(x,y)表示脉压后回波数据矩阵A中第x行第y列元素的大小,数据矩阵A中元素的最小值和最大值分别为Amin和Amax
(6)
步骤 1将区间[Amin,Amax]均匀划分为B个子区间,统计数据矩阵A中元素位于第b(b=1,2,…,B)个子区间的个数,记为nb,并将位于第b个子区间内的所有元素量化为fb。
nb=card({A(x,y)|A(x,y)∈[LbRb],
1≤x≤X,1≤y≤Y})
(7)
式中,Lb和Rb分别表示第b个子区间的左、右端点。
步骤 2计算第b个子区间量化值fb的出现概率pb。
(8)
步骤 3若分类阈值为g(g∈{f1,f2,…,fB}),则阈值g将B个子区间量化值分成两个集合C和D,分别表示为
(9)
进而得到集合C和D各自的先验概率pC(g)和pD(g),分别表示如下:
(10)
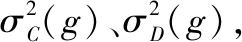
(11)
(12)
(13)
(14)
步骤 5计算当前分类阈值g对应的误差目标函数J(g)。
(15)
步骤 6将每一个子区间量化值fb(1≤b≤B)作为分类阈值g,重复步骤3~步骤5,求得使误差目标函数J(g)最小的子区间量化值,并将其作为最佳分类阈值gopt。
(16)
步骤 7利用步骤6中求得的最佳分类阈值gopt对脉压后回波数据矩阵A进行0-1二值化处理。
(17)
式中,A′(x,y)表示二值化处理后数据矩阵A′中第x行第y列的元素。经过Kittler算法二值化处理后,绝大部分噪声被抑制,而目标和密集假目标干扰被保留。
2.2 基于波形熵的干扰抑制
作为统计学中的一个概念,熵用于衡量随机变量的不确定性。而波形熵衡量了信号波形能量沿参数轴的发散程度。对于一个信号波形,若采样点的幅度沿参数轴大小相等,即波形能量均匀分布,则波形熵最大;相反,若只有部分采样点的幅度较大,波形能量集中,此时波形熵较小。从式(17)可知,脉压回波数据矩阵经Kittler算法0-1二值化处理后,目标运动轨迹为沿慢时间维的连续直线,波形能量均匀分布,即波形熵最大;而假目标运动轨迹为沿慢时间维离散的点,波形能量集中,即波形熵较小。因此,利用这种差异性,通过计算二值化处理后数据矩阵A′所有列的波形熵,可识别真实目标和假目标干扰,进而实现密集假目标干扰的抑制。

(18)

(19)

2.3 基于LOF算法的干扰旁瓣剔除
经过2.2节基于波形熵的干扰抑制处理后,密集假目标干扰被有效抑制,只保留了目标所在距离单元的回波数据。保留的回波数据中不仅包含目标回波信息,同时部分脉冲回波数据中叠加了密集假目标干扰的旁瓣。当干信比较低时,干扰旁瓣能量较小,对二维高分辨稀疏重构的性能影响较小。若在强对抗场景下,干信比较高,较强的干扰旁瓣会导致脉间积累后副瓣电平抬高,恶化基于稀疏重构的脉间相参处理算法性能,严重时将不能正确检测目标。
对此,采用LOF检测方法剔除干扰抑制后回波数据中的干扰旁瓣。LOF算法是数据挖掘中基于密度的离群点检测算法[24]。经过干扰抑制后的回波数据中,对于只含有目标信息的数据,其幅度分布在一个范围内,而叠加干扰旁瓣数据的幅度较大,并没有落在上述范围内,被视为离群点。因此,可以采用LOF算法剔除这些离群点。算法具体流程如下。
令S=[s1,s2,…,sM]T表示目标所在距离单元的回波数据,其中存在有较强的干扰旁瓣。
步骤 1对于向量S中的元素si,计算向量S中与si最近的第k个距离,称为si的第k距离,记为dk(si),这里的距离指的是欧式距离。
步骤 2将向量S中所有与元素si的距离不大于si的第k距离的元素构成的集合称为si的第k距离邻域,记为Nk(si)。
Nk(si)={sj||si-sj|≤dk(si),1≤j≤M,j≠i}
(20)
步骤 3计算元素si的局部可达密度ρk(si),表示如下:
(21)
式中,dk(si,sj)=max(|si-sj|,dk(si))。
步骤 4计算元素si的LOF表示如下:
(22)
LOF表示元素si的局部可达密度与其第k距离邻域内元素的局部可达密度的对比。若LOF大于8,表示元素si与其局部元素的密度差异较大,可认为元素si为离群点,予以剔除;若LOF接近于1,表示元素si与其局部元素的密度差异较小,可认为元素si为正常点,予以保留。
2.4 二维稀疏重构
经过上述处理流程后,可认为回波数据中只含有目标信号和噪声,表示为
(23)
在抑制干扰后,一个距离单元内的目标一般较少,目标场景具有稀疏性,则可以通过压缩感知进行高分辨的场景重构[25]。将感兴趣的距离-速度范围进行离散化,设离散化后的距离维、速度维格点数分别为P和Q,则
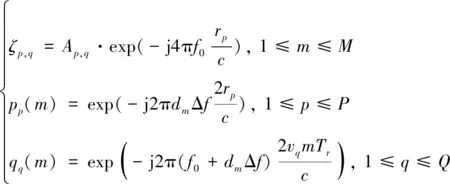
(24)
式中,ζx,y为目标散射系数;px(m)和qy(m)分别为距离和速度相位项。将距离和速度相位项做哈达马积构成如下观测矩阵:
式中,ep,q=pp(m)⊙qq(m),⊙表示哈达马积。式(23)所示的回波信号可以重新改写为
R=Ex+n
(25)

(26)
式中,ε表示噪声功率的估计值。
3 仿真实验与结果分析
3.1 仿真实验验证
本节按照第1.2节所述的密集假目标干扰信号模型构建典型密集假目标干扰场景,通过数字仿真实验验证基于波形熵的捷变频雷达抗干扰算法的有效性。仿真实验中,3个目标以及雷达工作参数如表1所示。将3个目标脉冲压缩后的回波信噪比均设置为5 dB。假设密集假目标干扰的个数为20,假目标之间的时延间隔分布在[150 ns 200 ns]区间内,对应的距离范围[22.5 m 30 m],干信比为45 dB。
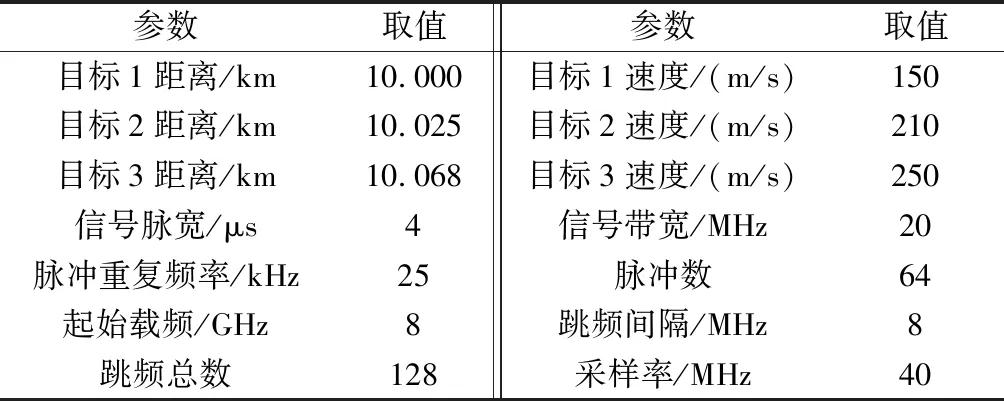
表1 仿真实验参数
基于波形熵的捷变频雷达抗密集假目标干扰仿真实验结果如图2所示。图2(a)为密集假目标干扰场景下捷变频雷达回波信号的脉冲压缩结果,通过脉冲间载频捷变能在频域上主动规避干扰信号。但是,载频捷变的随机性和盲目性导致部分脉冲回波信号中存在较强的干扰信号。未抑制干扰时的二维稀疏重构结果如图2(b)所示,此时3个真实目标被干扰完全覆盖。图2(c)为基于Kittler算法的噪声抑制结果,经过二值化处理后绝大部分的噪声被有效抑制,而目标和密集假目标干扰被尽可能的保留。同时,3个目标的运动轨迹均为一条与慢时间维平行的直线,而假目标干扰是一些明亮的点。图2(d)为波形熵结果,结果中有3个明显的峰值,波形熵峰值的横坐标对应目标所在的距离单元,进而可只保留目标所在距离单元的数据。图2(e)为干扰抑制结果,与回波脉压结果相比,密集假目标干扰被有效抑制。但是,回波中部分脉冲仍有较强的干扰主瓣和旁瓣,若直接进行二维高分辨稀疏重构,不仅会导致重构结果中的旁瓣抬高,也会产生虚假目标,如图2(f)所示。图2(g)为基于LOF算法的干扰主瓣和旁瓣剔除结果,与图2(e)干扰抑制结果相比,有效剔除了较强的干扰主瓣和旁瓣。图2(h)为干扰主瓣和旁瓣剔除后二维高分辨稀疏重构结果,由于剔除了较强的干扰主瓣和旁瓣,脉间相参处理后的虚假目标被有效抑制,3个真实目标能被重构出来。仿真实验验证了所提算法的有效性。


图2 抗干扰仿真Fig.2 Simulation of jamming suppression
3.2 算法性能分析
下面分析干信比对所提抗干扰算法性能的影响,同时与文献[22]中提出的基于形态学滤波的密集假目标干扰抑制算法进行对比。由于两种抗干扰算法采用不同的阈值分割方法进行二值化处理,因此对比分析干信比对两种阈值分割算法性能的影响。为定量评估阈值分割算法性能,定义目标信息保留百分比。这是由于相比于未被抑制的极小部分噪声对目标和干扰鉴别的影响,最大程度保留目标信息更有利于后续识别目标和干扰。其中,目标信息保留百分比这一指标的计算方法为二值化处理后目标所在距离单元被置1的脉冲数除以一个相干处理间隔内的脉冲数。性能分析中的雷达、目标及干扰参数与第3.1节仿真实验中设置的参数相同,其中干信比的变化范围为[20 dB,80 dB]。1 000次蒙特卡罗实验结果如图3所示,图中蓝色和红色曲线分别代表本文所用阈值分割算法和文献[22]中的阈值分割算法。可以看出,本文所用Kittler算法的目标信息保留百分比随干信比增加有微小波动,当干信比大于58 dB时急剧下降至15.6%。而文献[22]中Otsu算法的目标信息保留百分比基本不受干信比变化的影响。但是当干信比小于58 dB时,Otsu算法的目标信息保留百分比低于Kittler算法,即在一定干信比范围内从保留目标信息的角度来看,Kittler算法要优于Otsu算法。

图3 两种算法目标信息保留百分比随干信比变化曲线Fig.3 Curves of target information retention percentage changing with jamming to signal ratio using two algorithms
接下来在相同参数条件下对比分析两种抗干扰算法的目标检测性能。图4为两种抗干扰算法目标检测概率随干信比变化曲线,其中蓝色和红色分别代表基于波形熵和基于形态学滤波的密集假目标干扰抑制算法。

图4 两种算法在不同干信比下的检测概率Fig.4 Detection probability of the two algorithms under different jamming to signal ratios
从图4可以看出,对于文献[22]中基于形态学滤波的抗干扰算法,当干信比小于34 dB时,检测概率高于90%,即能够有效抑制干扰并检测目标;随着干信比进一步增加,检测概率逐渐降低;当干信比大于50 dB时,检测概率基本为0。而对于本文所提的基于波形熵的抗干扰算法,当干信比大于50 dB时,检测概率仍然高于90%,即能有效对抗干扰,这是由于采用LOF算法对目标回波中叠加有较强干扰旁瓣的数据进行剔除,有力提升了算法的抗干扰性能;随着干信比增大至60 dB时,检测概率急剧下降,接近于0,此时本文所提算法失效,这是由于二值化处理过程中真实目标被误分为噪声,导致二值化结果中并没有与慢时间维平行的直线,即目标的运动轨迹,进而不能有效识别目标,抑制干扰。因而,为了防止算法在高干信比条件下失效,在二值化过程中,可以将Kittler算法和Otsu算法相结合,即在低干信比条件下使用Kittler算法,在高干信比条件下使用Otsu算法。
4 实测数据验证
外场对抗试验中干扰机位于目标船舶上对雷达实施干扰,而雷达采用捷变频体制探测海上舰船目标。表2为外场试验参数。
图5为外场对抗试验数据处理结果。图5(a)为回波信号的脉冲压缩结果,部分脉冲沿距离维存在密集假目标干扰。图5(b)为噪声抑制结果,可见二值化处理后大部分噪声被抑制。此外,二值化后目标运动轨迹为与慢时间维平行的直线,而在快时间-慢时间二维平面上干扰呈现为散乱分布的点,根据二值化后目标和干扰的这一特性,利用波形熵可以鉴别目标和密集假目标干扰,波形熵结果如图5(c)所示。图5(d)为干扰抑制结果,与图5(a)脉冲压缩结果相比,有效抑制了密集假目标干扰。然而目标回波信号中仍有一个脉冲存在较强的干扰旁瓣,其会导致脉间相参处理结果中旁瓣抬高,因而需要剔除较强的干扰旁瓣。图5(e)为采用LOF检测算法剔除强干扰旁瓣的结果。对剔除强干扰旁瓣后的回波数据采用压缩感知算法进行稀疏重构,处理结果如图5(f)所示。外场实测数据处理结果表明了基于波形熵的密集假目标干扰抑制算法的有效性。

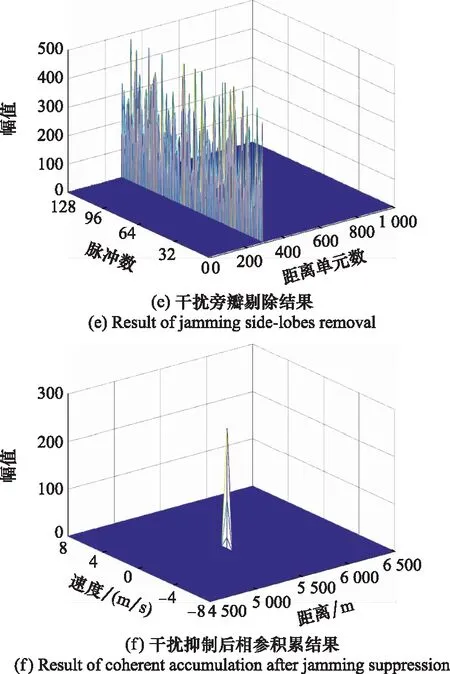
图5 实测数据抗干扰结果Fig.5 Jamming suppression result of measured data
5 结 论
密集假目标干扰不仅影响雷达目标检测,而且严重消耗雷达系统资源,使得雷达数据处理饱和。对此,提出了一种捷变频联合波形熵的密集假目标干扰抑制算法。与现有同类型抗干扰算法相比,本文所用二值化方法——Kittler算法在一定干信比范围内能更好地保留目标信息,有利于识别目标和干扰。此外,同类型抗干扰算法并没有剔除目标回波中叠加有强干扰旁瓣的数据,而本文采用LOF算法予以剔除,进而极大提高算法的抗干扰能力。数字仿真实验和外场实测数据处理结果验证了所提算法的有效性。算法性能分析结果表明,当干信比为58 dB时,本文算法仍能有效抑制干扰,正确检测目标。
