量测点迹空间聚类的多传感器多帧检测算法

张佳琦, 陶海红, 张修社

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西安导航技术研究所, 陕西 西安 710068)

0 引 言

传统的多目标跟踪方法利用传感器门限检测后的量测点迹进行多帧相关处理生成目标航迹,常用的方法包括全局最近邻跟踪算法[1]、联合概率数据关联算法[2]、多假设跟踪算法[3]、随机有限集跟踪算法[4]等。随着目标隐身特性的不断提升,传统的基于门限检测的多目标跟踪算法难以对隐身目标进行连续、稳定的跟踪。针对以上问题,有学者提出了多帧检测算法(multi-frame detection, MFD)[5-8],该技术联合处理多帧未经门限检测的原始数据,通过积累帧间量测点迹的幅度信息,实现微弱目标的检测。MFD算法的研究方向包括机动目标的MFD算法[9-12]、多目标场景的MFD算法[13-15]、多目标临近场景的MFD算法[16-17]、两级处理结构的MFD算法[18-19]、迭代框架的MFD算法[20-21]、针对检测场景的杂波分布和目标特性开展的MFD算法[22-23]等。然而,随着作战环境的日趋复杂,单装设备容易受到主/被动干扰产生大量杂波/噪声,导致单装设备的MFD算法运算复杂度高且虚假目标多。

利用多传感器组网不易受到干扰这一特性,有学者提出了基于多传感器组网的MFD算法,按照数据处理方式划分,多传感器MFD算法分为集中式MFD算法(centralize fusion MFD, CF-MFD)[24]和分布式MFD 算法(distributed fusion MFD, DF-MFD)[25-28]。其中,CF-MFD算法在融合中心处理全部量测点迹,能够充分保留多部传感器的原始量测点迹的幅度信息以提升微弱目标的检测概率,但会大幅增加算法的运算复杂度,且会产生大量虚假目标。DF-MFD算法在各传感器节点进行独立处理,通过分布式处理能够检测出大部分目标,将检测结果发送到融合中心进行融合,通过多传感器的相互印证形成融合结果,能够大幅降低算法运算复杂度,有效抑制虚假目标数量,但在融合处理过程中会丢失一部分有效信息,降低微弱目标的检测概率。

针对以上问题,利用目标量测点迹在多传感器之间的分布特性及目标能量的可累加性,提出一种量测点迹聚类的MFD(measurement plots clustering MFD, MPC-MFD)。该算法首先利用同源检测对多传感的器量测点迹的有效性进行判断实现杂波/噪声剔除,其次在空间和时间两个维度对目标的能量进行积累实现微弱目标检测。本文内容安排如下,第1节对检测场景、目标模型及相关符号进行描述;第2节阐述了本文所提算法框架,对算法步骤进行描述并分析了算法的运算复杂度;第3节通过仿真实验对算法的有效性进行验证;最后,提出了可用的结论。

1 场景与模型

1.1 检测场景

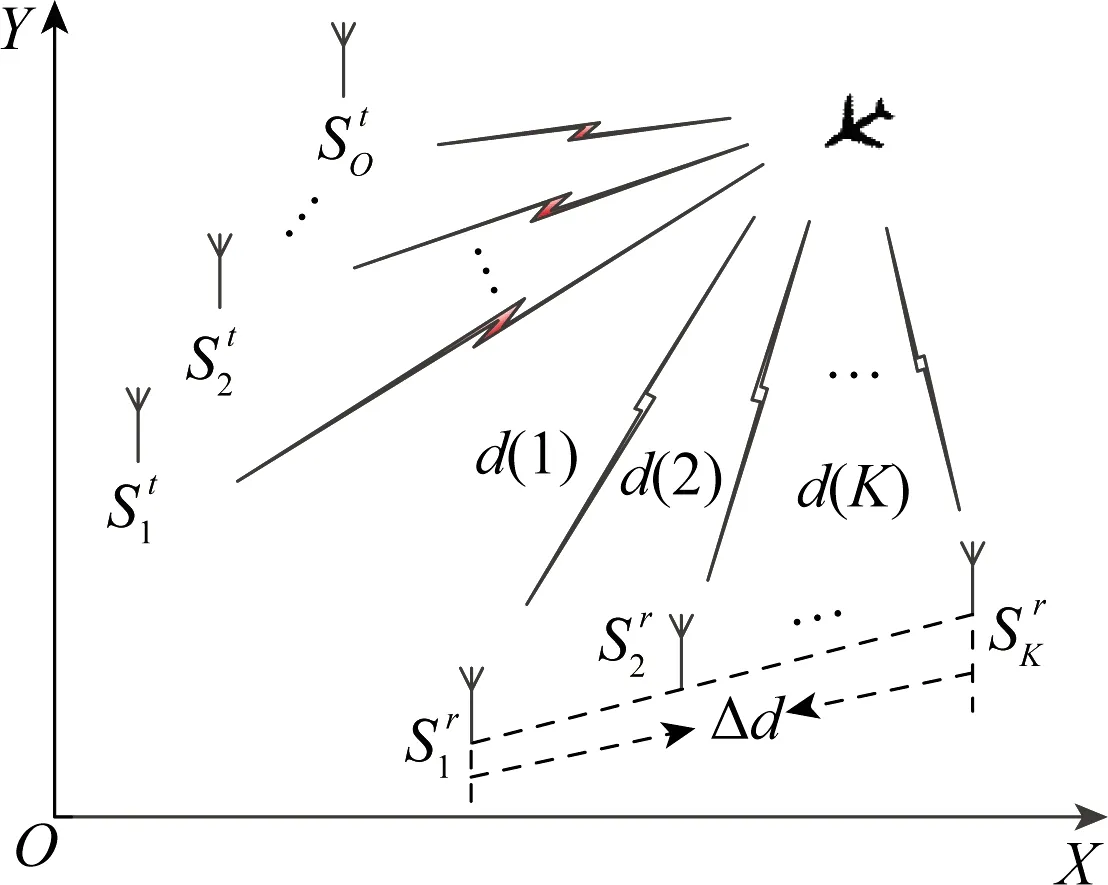
图1 多传感器检测场景Fig.1 Multi-sensor detection scenario

|d(1)-d(K)|<Δd

(1)

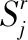
(2)

(3)

由此可知,不同传感器对同一目标的量测点迹在时间上是异步的。假定场景中目标最大运动速度为vmax,由传播时延导致目标在以上两部传感器生成的量测点迹的最大位置变化为

dmax=vmaxΔt

(4)

将式(3)代入式(4)可得

dmax=vmaxΔd/c

(5)

由vmax≪c可知,通过调整传感器之间的间距Δd,容易得到目标变化dmax满足:

(6)

1.2 运动模型

在包含M个目标的X-Y两维场景中,第m个目标的状态可以表示为Xm=[xm,vxm,ym,vym]T。其中,xm和ym分别表示目标在X维和Y维的位置坐标,vxm和vym表示目标在X维和Y维的速度坐标。目标的运动状态服从线性马尔可夫模型,过程噪声分布服从高斯白噪声。在笛卡尔坐标系下,近似匀速直线模型是一种典型的线性模型,目标的运动过程可以表示为

xm(l)|xm(l-1)～Ν(·;Fxm,Q)

(7)

式中,N(x;μ,Σ)表示高斯概率密度函数,μ为均值,Σ为协方差矩阵;F为状态转移矩阵;Q为过程噪声协方差矩阵:

(8)

(9)

式中,T表示连续帧之间的时间差;κ表示过程噪声强度;Ik表示单位矩阵;⊗表示克罗内克积。

1.3 量测模型

量测模型采用低检测门限结构,能够剔除低门限杂波/噪声似然点迹,保留高门限目标似然点迹,从而降低量测空间中量测点迹的数量。该检测结构不需要对量测空间进行离散化,直接处理过门限量测点迹队列。第k(k=1,2,…,K)个传感器的点迹队列表示为

(10)

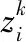
(11)

式中,ti表示量测点迹的录取时间;pi表示量测点迹的检测位置;Ai表示量测点迹的回波信号幅度信息。量测点迹的信号幅度可表示为

(12)

式中,H0假设没有目标存在;H1假设有一个目标存在。另外,as表示目标回波信号幅度,nH1和nH0分别表示独立同分布的零均值高斯噪声过程,协方差分别表示为σH1和σH0。

2 本文所提算法

2.1 算法框架

针对强干扰环境下利用单传感器MFD算法进行微弱目标检测时,经过低门限检测后保留大量杂波/噪声等干扰,导致算法运算复杂度高、虚假目标数量多。本文参照图1所示的多传感器组网探测场景,利用目标量测点迹在多传感器之间的分布特性及目标能量的可累加性,提出一种多传感器MFD算法,该算法的处理框架如图2所示。

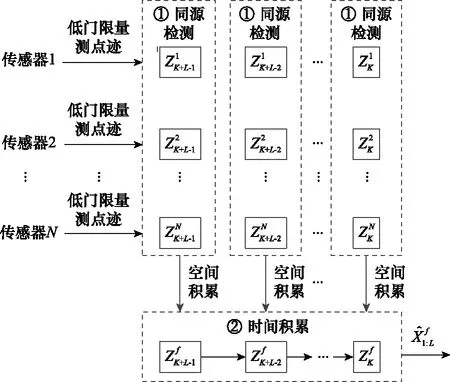
图2 多传感器MFD算法框图Fig.2 Algorithm diagram of multiple sensors MFD

2.1.1 同源检测

利用目标量测点迹在多传感器之间的分布特性,通过同源检测对目标量测点迹的有效性进行判断。同源检测原理即假定多传感器对真实目标的量测点迹相对“集中”,而多传感器对虚假目标的量测点迹相对“分散”。通过计算目标在多传感器中的检测特征值,并判断目标的检测特征值是否满足同源检测门限:

(13)

式中,K为参与组网传感器数量；Hi为传感器i对目标的检测特征函数；γ为同源检测门限。保留满足同源检测约束目标的量测点迹,剔除不满足同源检测约束目标的量测点迹,从而实现杂波/噪声剔除。

2.1.2 空-时能量积累

利用多传感器对微弱目标在空间上的回波能量和多帧对微弱目标在时间上的回波能量进行两维积累,实现微弱目标的检测:

(14)

(15)

本文旨在提出一种多传感器的MFD算法思想,综合考虑目标量测点迹在多传感器间的分布特征和在多帧间的运动特性,通过空-时能量积累实现微弱目标检测。在算法具体实现过程中采用文献[29-30]提出的聚类算法实现多传感器同源检测和目标空间维度的能量积累,利用文献[16-18,20]提出的基于量测点迹集合的动态规划MFD(dynamic programming MFD DP-MFD)实现目标时间维度能量积累。另外,与文献[24]和文献[25]提出的多传感器MFD算法相比,该算法的主要优点包括:

(1) 利用目标量测点迹在多传感器之间的分布特性,通过同源检测剔除针对单传感器的主/被动干扰,降低强干扰环境下量测点迹的数量,降低MFD算法的运算复杂度;

(2) 利用目标能量的可累加性,在空间上对多传感器量测点迹进行回波能量积累,在时间上对多帧间的量测点迹进行回波能量积累,通过空间、时间两维能量积累提升微弱目标的检测概率。

2.2 算法步骤

为了对多传感器的量测点迹进行同源检测实现强干扰环境下的杂波/噪声剔除,利用空间聚类算法将多传感器对同一目标的量测点迹进行“集中”,将不同目标的量测点迹进行“分离”,对目标和杂波/噪声进行识别;同时,通过对多传感器和多帧间的量测点迹的幅度进行积累,通过积累目标空-时两维幅度提升微弱目标的检测概率。为了实现上述目标,本文提出了MPC-MFD算法,该算法对多传感器低检测门限检测后的量测点迹进行处理以实现微弱目标检测。

2.2.1空间聚类

(1) 多源聚类

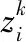
(16)

(2) 子类划分

考虑单个聚类内可能包含多个目标的情况,利用聚类划分实现多目标检测。单个聚类内目标数量计算表示为

(17)

(3) 门限检测

γ=qK

(18)

式中,q为调节系数,当q较大时,要求目标能够被大部分传感器检测到,此时目标的检测概率和虚警概率均会下降。当q较小时,仅要求目标被小部分传感器检测到,此时目标检测概率和虚警概率均会提升。因此,该系数的设定需要在目标检测概率和虚警率之间进行平衡。

(4) 量测融合

利用空间聚类结果对聚类内量测点迹的状态进行融合,通过融合处理能够提升量测点迹的探测精度,聚类Cn的等效量测点迹的状态为

(19)

聚类Cn的等效量测点迹的量测误差协方差矩阵为

(20)

对聚类内量测点迹的幅度进行积累,通过幅度积累能够提升微弱目标的回波幅度,聚类Cn的等效量测点迹幅度为

(21)

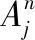
2.2.2 DP-MFD检测

(1) DP积累

在多帧之间采用基于DP-MFD算法,对目标的量测点迹的幅度进行积累,计算检测目标的得分函数F(ξ)及可回溯状态τ(ξ):

(22)

(23)

(2) 有效性检测

通过式(22)和式(23)分别对目标在多传感器和多帧间的量测点迹进行幅度积累,提升微弱目标的回波幅度。对比检测目标的得分函数与检测门限γ1,实现检测目标的确认或删除:

(24)

MPC-MFD算法处理步骤伪代码如下。

算法1 MPC-MFD1. Space Clustering2. for i=1:plotNum do3. for j=1:plotNum do4. 利用式(16)计算量测点迹之间的相关性5. 对满足相关性要求的量测点迹标记相同标签6. end for7.end for8. 利用式(17)将超尺寸聚类分解为多个子聚类9. 利用式(18)对聚类集合进行门限检测10.利用式(19)～式(21)计算聚类集合的等效量测点迹11. DP-MFD12. for i=1:trackNum do13. 利用式(22)和式(23)计算得分函数和回溯函数14. 利用式(24)判断航迹的有效性15. end for

2.3 算法复杂度分析

MPC-MFD算法的运算复杂度主要包括多传感器量测点迹空间聚类和L帧DP-MFD算法运算两部分。多传感器量测点迹空间聚类时间复杂度表示为

O1(MPC-MFD)=

(25)

式中,Nplot为单帧中量测点迹平均数量;Cplot为量测点迹空间聚类标签标记次数。假定多传感器的量测点迹数量服从独立同分布,单帧中量测点迹的平均数量Nplot表示为

Nplot=(NrNq-Ntrack)·FAR+Ntrack·PD

(26)

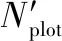
(27)

式中,FAR′为K个传感器的联合虚警率;PD′为K个传感器的联合检测概率,FAR′和PD′均服从二项分布。

PD′～B(K,PD)

(28)

则有

(29)

由式(29)可知,PD′和FAR′的大小由调节系数q确定,q的设定需要在PD′和FAR′之间进行平衡,在保证一定的PD′条件下,使得FAR′取最小,从而有

(30)

另外,单传感器的L帧DP-MFD算法运算复杂度主要由状态转移集合计算和航迹构建两部分构成,其中状态转移集合计算的运算复杂度为

(31)

式中,P为航迹构建时允许连续缺失点迹数量;L为单传感器DP-MFD积累的量测帧数。航迹构建的过程实质上是在迭代的更新状态转移集合,每次航迹构建过程生成w个目标,航迹构建运算复杂度为

(32)

因此,MPC-MFD算法L帧DP-MFD算法运算表示为

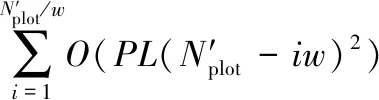
(33)

由此可知,MPC-MFD算法运算复杂度表示为

O(MPC-MFD)=

(34)

由式(34)可知, MPC-MFD算法运算复杂度与MFD算法积累帧数L、单帧中量测点迹数量Nplot、参与组网传感器数量K等参数成正比关系,量测点迹空间聚类标签标记次数Cplot及调节系数q与算法成反比关系。

表1 算法运算复杂度分析

O(MPC-MFD)≈O(DF-MFD)<

O(CF-MFD)

(35)

3 仿真实验

3.1 仿真场景

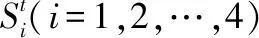
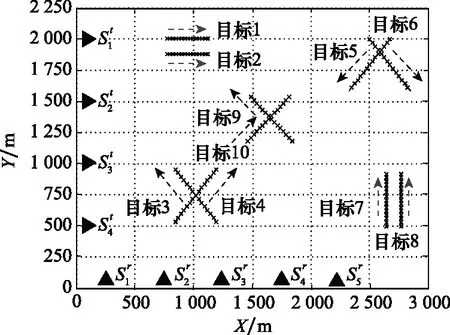
图3 多传感器多目标仿真场景Fig.3 Multi-sensor multi-target simulation scenario

参与组网传感器数量K=5,传感器具有相同的量测误差R=[10 m,10 m]。量测空间聚类度量函数d为欧式距离,ε为3倍传感器量测误差,调节系数q=0.5。DP-MFD算法多帧积累的帧数L=10,航迹构建时允许连续缺失点迹数量P=3,最大速度vmax=600 m/s。检测门限γ1由105次蒙特卡罗仿真实验确定。仿真环境设定杂波/噪声服从高斯分布,针对不同的FAR选定目标的信噪比(signal to noise ratio, SNR)从1～10 dB开展10次仿真实验,每次实验采用100次蒙特卡罗实验。采用的评估指标分别为有效检测航迹数(真实航迹被检测到的数量)和虚假航迹数(虚假航迹被检测到的数量)。

3.2 性能分析

图4为FAR分别为10-1、10-2和10-3时,3种检测算法在不同SNR下的有效目标检测数量对比图。图5为FAR分别为10-1、10-2和10-3时,3种检测算法在不同SNR下的虚假目标检测数量对比图。由图4(a)和图5(a)可知,在FAR为10-1时,当目标SNR为1～2 dB时,3种检测算法均无有效检测目标输出,仅CF-MFD算法有少量虚假目标。由图4(b)和图5(b)可知,在FAR为10-2时,当目标SNR为1～3 dB时,3种检测算法均无有效检测目标输出,仅CF-MFD算法有少量虚假目标。由图4(c)和图5(c)可知,在FAR为10-3时,当目标SNR为1～4 dB时,3种检测算法均无有效检测目标输出。原因是在以上情况下目标的大部分量测点迹被检测门限剔除,导致真实目标难以被检测。而CF-MFD算法采用串行处理机制在低SNR时,可以将少量真实量测点迹与杂波/噪声关联起来形成虚假目标。由图4(a)和图5(a)可知,在FAR为10-1时,当目标SNR为3～6 dB时,CF-MFD算法的有效检测目标数优于MPC-MFD算法,且均优于DF-MFD算法。由图4(b)和图5(b)可知,在FAR为10-2时,当目标SNR为4～6 dB时,CF-MFD算法的有效检测目标数与MPC-MFD算法相当,且均优于DF-MFD算法。由图4(c)和图5(c)可知,在FAR为10-3时,当目标SNR为5～6 dB时,CF-MFD算法的有效检测目标与MPC-MFD算法相当,且均优于DF-MFD算法。原因是CF-MFD算法采用串行处理机制在低SNR时,可以将少量真实量测点迹关联起来形成有效检测,同时CF-MFD算法也更容易产生虚假目标。MPC-MFD算法采用量测点迹空间聚类机制,能够通过空间聚类对杂波/噪声进行抑制,在低SNR时导致真实量测点迹被剔除。DF-MFD算法,采用不同传感器构建的目标进行相互印证,能够抑制虚假目标的同时会丢失真实目标。由图4和图5可知,在FAR分别为10-1、10-2及10-3时,目标SNR为7 dB以上时,3种检测算法均能有效检测目标,且几乎不存在虚假目标。原因是目标的真实量测点迹通过门限检测被保留下来,形成有效检测目标。而杂波/噪声形成的虚假目标与真实目标的幅度似然比低,识别为虚假目标被剔除。

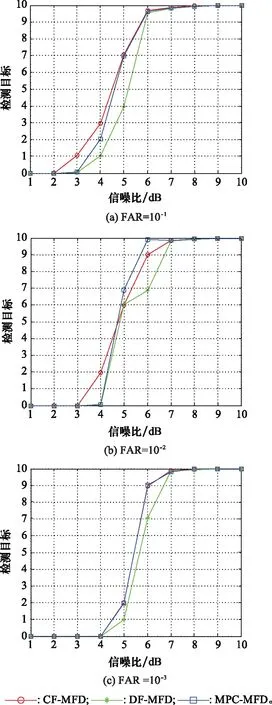
图4 有效目标检测数Fig.4 Number of declared targets

图5 虚假目标检测数Fig.5 Number of false targets

由表2可知,当FAR分别为10-1、10-2及10-3时,MPC-MFD算法的运算复杂度与 DF-MFD算法相当,且均大幅低于CF-MFD算法。在不同FAR下,MPC-MFD算法和DF-MFD算法的运算复杂度相对CF-MFD算法减少约80%。

表2 算法运行时间比较

4 结 论

针对多传感器检测信息的有效融合来提升多传感器协同探测效能这一关键技术,本文对多传感器组网下的MFD算法开展研究。设定一种多传感器组网下的探测场景,利用多传感器的同源检测原理,提出了一种多传感器量测点迹聚类的MFD算法。通过算法分析和仿真实验可知,本文所提算法的运算复杂度与DF-MFD算法相当,当传感器数目较大时,较CF-MFD算法下降约80%;本文所提算法的虚假目标抑制性能优于DF-MFD算法及CF-MFD算法;另外,本文所提算法对微弱目标的检测性能与CF-MFD算法相当,优于DF-MFD算法。从而验证了该算法的有效性和工程的可行性。