改进的自适应NSGA-II求解多目标流水车间调度问题

张 伟

(福建船政交通职业学院通用航空产业学院，福建福州 350007)

0 引言

针对流水车间调度问题，调度问题学者Johnson[1]起先于1954年发表行之有效的算法，至此许多学者纷纷加入研究流水车间调度问题行列，取得了大量的研究成果.其中多是关注解决单目标问题，即构建最大完工时间最小为优化目标模型[2,3]，除此之外，还有最小化最大延迟时间[4]和总流程时间[5]等，它们是衡量生产经济效益、关乎调度成本的重要指标.可是面对竞争越来越激烈的产品制造行业，经营者往往要思量两个及以上优化目标，而这些目标之间存在矛盾关系.从而，在流水车间调度中琢磨其多目标问题就显得越有工程价值.

宋存利[3]设计了一种改进贪婪遗传算法，应用逆序解码和正序解码、贪婪交叉算子、贪婪变异算子，用于改善最大完成时间目标，使其达到最小.王宇等[6]构思了实数编码、差分进化变异、混合采样的多目标差分进化算法，用以最小化最大拖期和最大完工时间.张闻强等[7]提出一种快速多目标混合进化算法，用以解决双目标的流水车间调度问题，为使最大完工时间和总流经时间最小并取得最佳.罗哲[8]设想了一种混合遗传算法，通过灰熵并行关联度作为算法适应值挑选子代，并建立Pareto外部档案、使用Pareto排序和拥挤距离计算，用以在流水车间调度问题中优化最大拖期时间、总流程时间和最大完成时间三个目标.

基于以上文献分析，许多学者探究的重点是两个目标的优化问题，也有少部分关注三个目标优化问题的钻研，并且研究成果多数是通过多目标进化算法求得.因此，本文按照某企业流水车间的一条实际生产线调度环境，综合考虑了最大完工时间、总拖期时间和总流程时间最小三个目标并为此构建调度模型，通过带有自适应参数调节改进的NSGA-II算法在调度解空间找寻Pareto解集，将数据进行加权处理挑选出中意的调度方案，表明该算法在解决多目标流水车间调度问题上是可行的、有效的.

1 流水车间调度问题描述和数学模型构建

1.1 流水车间调度问题描述

流水车间调度问题通常描述如下：n(w1,w2,…,wn)个产品在m(M1,M2,…,Mm)台机器上进行生产，每个产品都要进行p道工序的生产，每台设备分配不同的工序进行生产.第i个产品的第j道工序表示为Rij，第u个产品的第j道工序表示为Ruj，n个产品的p道工序具有一样的加工路径，即不同产品的相同工序是在相同的机器上生产，表示为M(Rij)=M(Ruj)，其中i≠u，i，u=1,…,n；j=1,…,p.Rij被分配在设备Mg(g=1,2,…,m)上进行生产，则其生产时间表示为Tijg.在一般流水车间调度问题中，一台设备被唯一分配一道工序进行生产，生产设备不能挑选，即p=m.已知每台设备上生产产品的的时间，要求明确设备上生产产品的次序，其目的是获得多目标函数的Pareto前沿.而且流水车间调度问题又符合普遍性的约束要求与设想[9].

1.2 数学模型构建

Cw11=Tw11

(1)

Cw1g=Cw1g-1+Tw1g;g=2,...,m

(2)

Cwi1=Cwi-11+Twi1;i=2,...,n

(3)

Cwig=max(Cwi-1g;Cwig-1)+Twig;i=2,...,n;g=2,...,m

(4)

鉴于流水车间的生产效率最大、资源配置合理和库存最小以及符合用户对产品订单的时间预期，本文考虑以使最大完工时间f1=Cmax、总流程时间f2=Ctotal和总拖期时间f3=Detotal最小的优化目标，即f=min(f1,f2,f3).其中：

(1)最大完工时间相应的目标函数Cmax：

Cmax=max(Cwim|i∈1,2,...,n)

(5)

(2)总流程时间相应的目标函数Ctotal：

(6)

(3)总拖期时间相应的目标函数Detotal：

(7)

其中：

2 自适应参数的NSGA-II算法设计

关于多目标优化问题的求解，呈现出许多多目标优化算法，有模拟退火算法、粒子群优化算法、遗传算法等.模拟退火算法采取冷却表进行探寻，模拟物理学中金属的平缓冷却过程规律，通常选取变权重措施开展目标函数加权组合，其实现过程慢且收敛能力尚待加强.粒子群优化算法采取类似于蜜蜂采蜜、蚂蚁觅食、鸟群捕食等行为的原理，经由粒子在探寻空间追随最佳粒子进行探寻，如果该粒子赶上粒子群目前的最佳粒子，出现种群多样性会丢失、早熟问题，同时如果粒子群的目前最佳值和一个粒子的目前位置与该粒子的目前最佳值一致，致使算法无法收敛.多目标遗传算法(MOGA)在Pareto支配等级基础上可以获取分布匀称的适应度，其采用适应度共享方法可以实现在选择压力适合的条件下维系整个种群的适应度为常数，然而由Pareto支配关系确定等级的方法可能使选择压力较大而导致非成熟收敛，如果一样的目标函数值对应于多个不同的非支配解，MOGA不易找出多个解.Pareto小生境遗传算法通过非支配关系进行联赛选择，且通过小生境技术来共享适应值维系种群多样性，其可以得到不差的Pareto前沿，缺点是比较集大小的拣选与小生境半径拣选没有一个一致的规范.而带精英策略的快速非支配排序遗传算法(NSGA-II)[10]选择一种快速非支配排序方法，使计算复杂度减少；利用拥挤距离和拥挤比较算子获取匀称的Pareto前沿，用于维系种群多样性；提出卓越解保存准则，将父代中卓越解保存，从而优化越恰当.本文通过NSGA-II算法来处理第1方面提出的多目标流水车间调度问题，采用自适应参数与NSGA-II算法结合以达到动态调节交叉、变异算子的目的，确保不丢失最佳解.

2.1 编码

在流水车间调度问题中，产品在机器上加工路径相同，不同工序在不同的机器上进行加工，因而算法选择采用基于产品的编码方式，即n个产品排列组合生成染色体，每条染色体中产品的先后次序代表一种调度信息.例如，7个产品在流水生产线上制造加工，假设一组产品的排列是w7、w1、w2、w3、w4、w6、w5，就体现一种调度策略W=7，1，2，3，4，6，5.

2.2 Pareto排序

对种群I进行非支配排序是为了获取种群中支配个体i的非支配数ni和被个体i支配的支配集Pi.其详细实施过程如下：

国企面临的另一重大冲击来自乡镇企业。当时，乡镇企业在江苏南部和山东的胶东半岛迅速发展起来，乡镇企业因为机制灵活在竞争中明显优于国有企业，并出现了“星期天工程师”现象：国有企业的技术人员，星期天到附近乡镇企业“走穴”，进行技术支持。

(1)对比种群中的两个个体i与j，当i好于j时，Pi=Pi∪{j}；当i差于j时，ni=ni+1；如果ni=0，则

Frank=Frank∪{i}.

(2)Pt是目前集合Frank中的每个个体t所支配的个体集合，针对Pt中保存的每个个体q，执行nq=nq-1步骤，若nq=0，则R=R∪{q}.

(3)非劣等级rank=1，即Frank=F1是第一非劣等级的个体集合，循环执行rank=rank+1，R=Frank步骤，直至种群中全部个体被非劣排序为止.

2.3 拥挤距离

为了维护种群多样性，算法定义拥挤距离来确保Pareto解集可以约束到一个分散匀称的Pareto前沿.其计算公式为：

(8)

其中：d(k)distance是第k个个体的拥挤距离，f(k+1).e、f(k-1).e分别是第(k+1)、(k-1)个个体第e个目标分量的函数值，femax、femin分别是第e个目标分量的函数值最大值与最小值.

2.4 选择

选择使种群演变朝向Pareto最佳解的方位逼近，以确保Pareto前沿匀称分散.算法采用二元联赛选择，其原理为随便遴选两个个体i与j进行比较，选择最优的个体进入下一代种群，鉴别个体i好于j的标准如下：非劣等级rankj>ranki；或ranki=rankj，而拥挤距离d(i)distance>d(j)distance.

2.5 交叉

交叉是种群演变进化的核心算子，它可以扩大算法搜索新空间的可能性，但也得考虑演变的约束性问题.交叉算子总是期盼能获取一些有效的新个体样式，却又能较大程度地保护代表卓越基因的卓越样式.本文选用部分匹配交叉，其整体探寻成效较优，不轻易陷进局部最优，确保经过遗传最佳样式能够最大程度地得到保留.如图1所示，依据I中两个父代个体g1、g2动态获取的两个交叉点以得到一个匹配段，比如3、5是选定的位置；由选定的位置之间所构成的匹配段确定部分映射关系为4-6、2-5、7-2，将两个交叉点之间的染色体部分交换，得到如II中g1，、g2，；根据匹配段交叉点之间基因映射关系，将g1，、g2，交换区域之外的一样的基因一一交换，从而获得III中子代个体h1、h2.

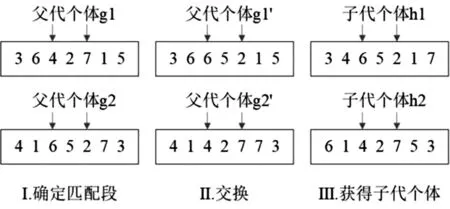
图1 部分匹配交叉Fig.1 Partial matching crossover

2.6 变异

变异实现种群演变收敛进程中防止陷入局部最优功能，可以增加种群的多样性.本文选用对换操作变异，通过动态方式在一个个体上生成两个变异位置，将这两个变异位置相应的染色体编码互换.比如2、6是变异的位置，图2所示为其操作过程.

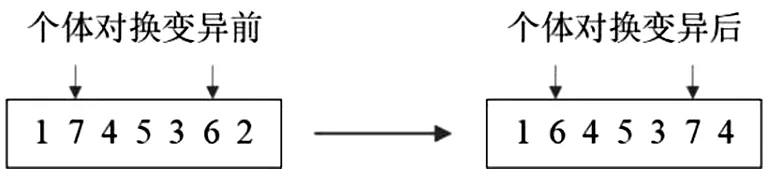
图2 对换变异Fig.2 Swapping mutation

2.7 自适应参数调整策略

采用基于进化阶段的自适应方法作为个体交叉率与变异率的调整方法[11].第一，要明确划分进化阶段，在同一进化阶段中进行个体交叉率与变异率设置，在不同进化阶段中设置交叉率和变异与基于进化阶段的自适应方法一样.当进化代数增加时，不同阶段个体交叉率与变异率呈线性下降走向，直至它在数值上与下一阶段的初始交叉率与变异率相等为止.第二，为了确保在进化后期个体也还有一定的几率参与进化，该方法中的交叉率与变异率会伴随进化代数的增加逼近一个趋近于0但不等于0的值.自适应交叉率与变异率的模型的两个部分如下：

(1)当非支配解个数小于10时，个体交叉率与变异率的模型为：

(9)

(10)

(2)当非支配解的个数不小于10时，该情况下的个体交叉率模型不变，而变异率的模型为：

(11)

其中：Pc是个体的交叉率，Pm是个体的变异率，N是算法的最大迭代次数，L是个体的编码长度.N1=αN，N2=(1-α)N.β是进化后期阶段交叉率与变异率的调节参数，β∈(0,1].0～N1为算法的进化初期阶段，N1～N2为算法的进化中期阶段，N2～N为算法的进化后期阶段.

2.8 精英保留策略

为了防止父种群中卓越的个体流失，而直接将其放到子种群中，算法引入精英保留策略，使种群演变收敛得到保证.算法执行的过程是：首先生成复合种群G，它是由父代种群P与子代种群Q组合形成；然后将快速非支配排序和拥挤距离计算应用到复合种群G中；最后选取卓越的个体形成新一代种群H，这个过程在复合种群G中进行.算法的详细过程如图3所示.

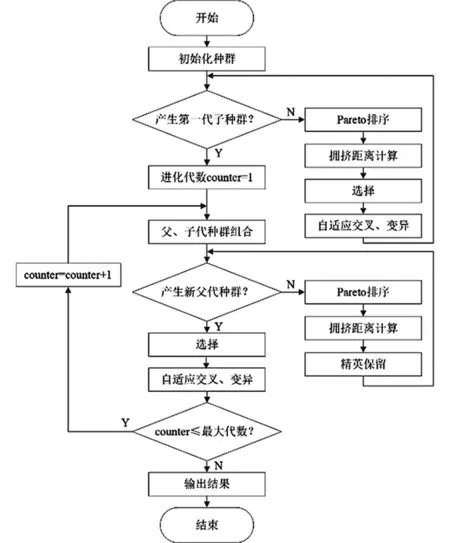
图3 改进的自适应NSGA-II流程Fig.3 Improved adaptive NSGA-II process

3 实例

3.1 基础数据

某企业有一条流水线采用8台设备生产7件产品.鉴于流水车间的生产效率最大、资源配置合理和库存最小以及符合用户对产品订单的时间预期，需要考虑以使最大完工时间、总流程时间和总拖期时间最小的优化目标，从而使产品产能生产最大化，提升经济收益.已知每个产品的交货期如表1所示，每个产品每道工序的生产时间如表2所示.运用MATLAB R2016a来编写算法的函数文件、脚本文件，并通过仿真优化获取几组较好的产品生产排序.

算法的有关系数设置：种群规模取400，进化代数取150，α取0.37，β取0.4.

3.2 结果输出

运行算法程序，输出获得如图4、5、6所示的每个目标函数的最佳解及其特性追踪，如图7所示的Pareto非支配解集.如表3所示为每个Pareto非劣解的3个目标函数值及其相应的生产排序.

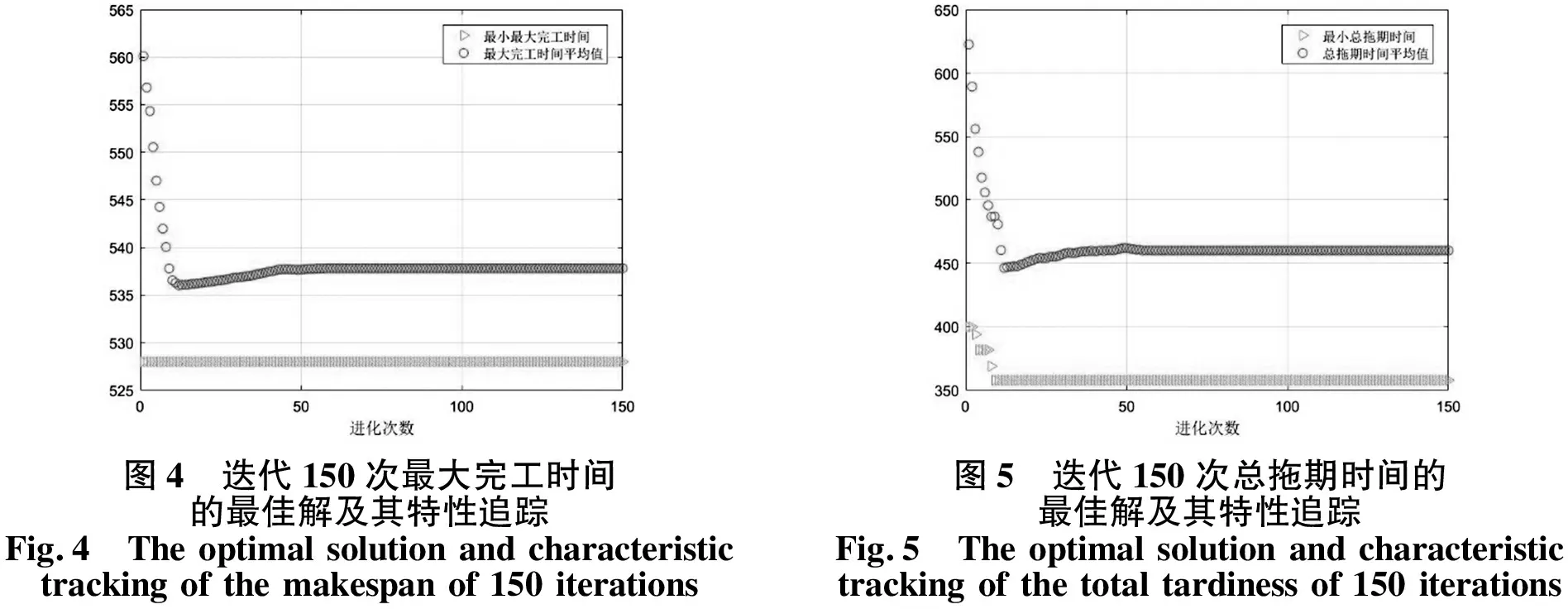
图4 迭代150次最大完工时间的最佳解及其特性追踪Fig.4 The optimal solution and characteristic tracking of the makespan of 150 iterations图5 迭代150次总拖期时间的最佳解及其特性追踪Fig.5 The optimal solution and characteristic tracking of the total tardiness of 150 iterations

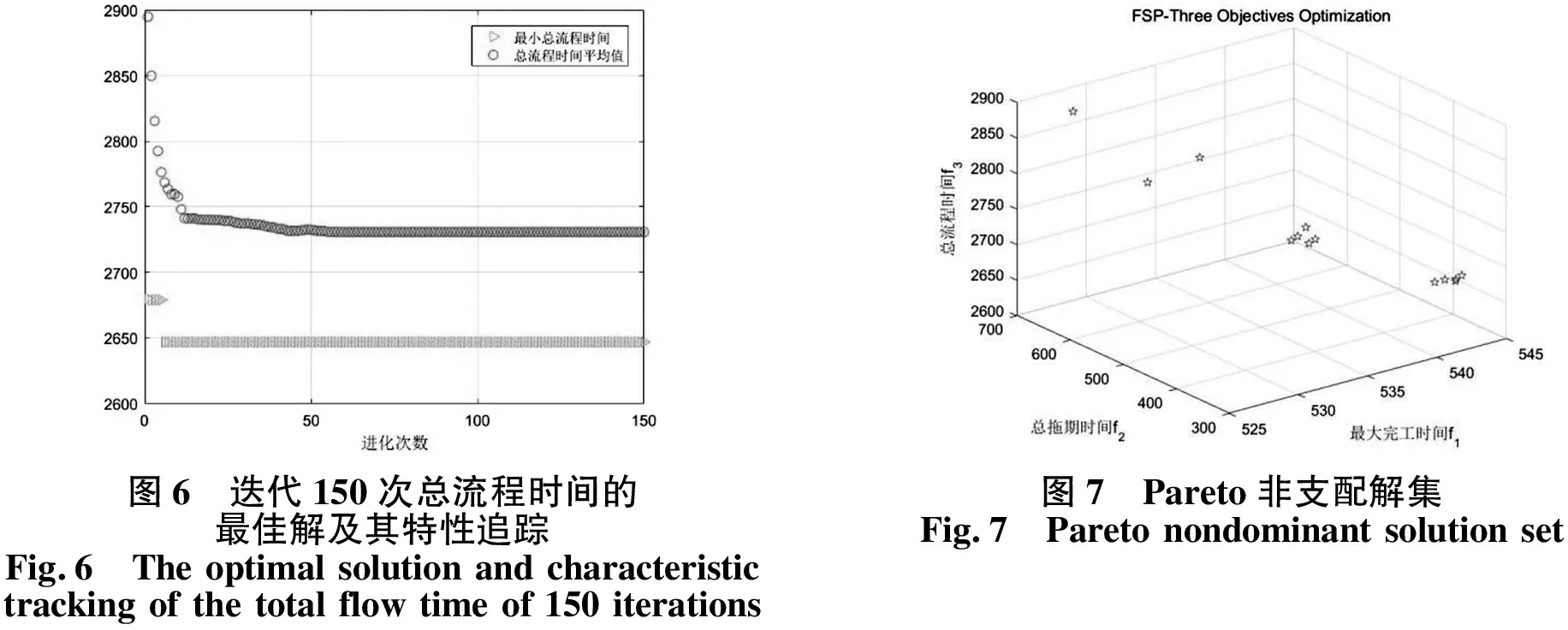
图6 迭代150次总流程时间的最佳解及其特性追踪Fig.6 The optimal solution and characteristic tracking of the total flow time of 150 iterations图7 Pareto非支配解集Fig.7 Pareto nondominant solution set

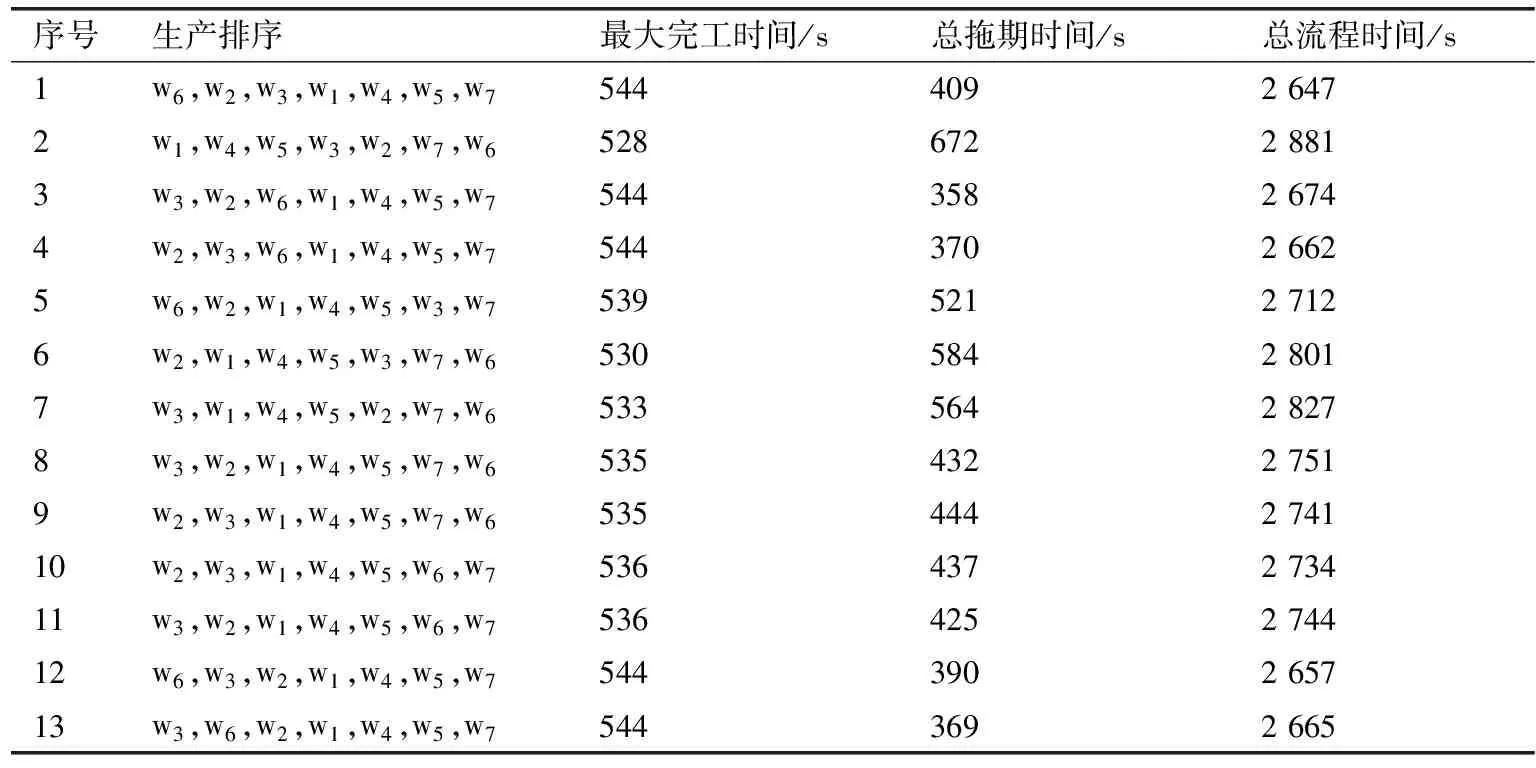
表3 Pareto非支配解集Tab.3 Pareto nondominant solution set

3.3 结果分析

由图4、5、6能够得出，3个目标函数的均值靠近最佳解，算法趋向收敛.依据图7、表3能够得出：序号为2的解的总拖期时间和总流程时间对比其余12组解都大很多，但由于其最大完工时间最小，所以每次迭代都能探寻到该解；序号6和7的解的最大完工时间都较小，但其总流程时间都较大；剩下10组解的3个目标函数值都较好，且布局比较匀称.运用Pareto非劣解集于流水车间调度中，生产者可以考虑实际加工条件下目标的主次之分，确定从优化所得的结果中遴选满意的调度方案，达到符合实际的生产供给目的.比如，对于该企业的流水线，考虑当前最重要的是最小化产品的总拖期时间，所以对3个目标分别给予0.1、0.7和0.2的权重，将3个目标进行归一化处理，获取最好调度方案是w3,w2,w6,w1,w4,w5,w7.

4 结论

本文按照流水车间调度问题的理论与特征，创建以最小化最大完工时间、总拖期时间与总流程时间为优化目标的调度模型，同时结合某企业的流水线具体调度情况，使用带自适应参数的改进NSGA-II算法求解该模型，获取了比较中意的调度方案，表明NSGA-II算法在解决多目标流水车间调度问题上是可行的、有效的，并且为企业提供生产调度排序举措参考.