用量子统计方法对双原子分子气体振动热容量的研究

刘国跃

(绵阳师范学院数理学院，四川绵阳 621006)

0 引言

在物理专业课程教学中，首次遇见双原子分子气体的振动热容量是在“热学”课程中，那里根据能量按自由度均分定理(简称能均分定理)，理想气体的摩尔热容量按照cv=(t+r+2s)/2确定(R为普适气体常数)，摩尔振动热容量则为cv=sR，s是振动自由度，双原子分子理想气体的摩尔振动热容量则为R.接着给出了在0 ℃到1 400 ℃范围内氢、氧、氮和一氧化碳的热容量实验值并与能均分定理的预期进行了比较，说明了能均分定理的近似性乃至于谬误.紧接着给出了氢气在0 ℃到1 400 ℃范围内的热容量，说明在这不到3 000 ℃的范围热容量的变化巨大，不是常量，并分析了经典理论的缺陷，指出了从量子力学解决该问题的方向[1].后来，在“热力学统计物理”课程中，讨论双原子分子气体的振动热容量时，将双原子分子的内部振动视为简谐振动，采用了量子力学的能级公式ευ=ħwe(v+1/2)，在求配分函数及后续热力学量(包含振动热容量)时，对无限个简谐振动能级求和并将求和转换为积分，得到了双原子分子气体振动热力学性质的解析结果(简称为谐振子结果SHO)，这在中外教科书中均有展示[2-3]，似乎问题已经解决.

我们将双原子分子溴化碘气体的振动热容量的SHO结果与实验数据进行比较，结果发现，在温度较低即振动激发很不充分时两者差异较小，但随着温度升高，两者差异逐渐加大，在较高温度例如1 500 K时，SHO结果明显低于实验结果，相对误差已经高达10%.这再次暴露出SHO结果的缺陷和谬误，这就需要说明，采用什么样的分析方法获得的结果才是逻辑严密的可信的.

1 对双原子分子内部振动的正确分析

将经典连续变化的振动能量改为采用量子化的简谐振动能级ευ=ħwe(v+1/2)(v是振动量子数)是一个进步，但应用于计算双原子分子气体的配分函数并对无限振动能级求和，还有几点不足：1) 双原子分子的内部振动实际上不是简谐振动，把不是简谐振动的实际情况仍然简化为简谐振动是不合理的.2)要正确求解双原子分子振动能级，应以物理性质良好的势能函数为基础，采用量子力学方法求得.图1给出了振动能级分布的大致情况，其中绿色是谐振子模型(Harmonic)下振动能级均匀分布，深蓝色是Morse势[4]导致的比较真实的双原子分振动能级的非均匀分布，随着振动量子数的增大，能级间隔会减小.借助MS势(Murrell-Sorbie)[5]和ECM势[6-7](Energy -consistent-method)等，都能求得类似于图1的双原子分子的振动能级分布.1932年，Dunham提出了包含高阶修正、形式简单优美的双原子分子振动能级解析公式[8]，但由于没有限定振动量子数的取值和高阶振动光谱系数不好确定，未见采用Dunham振动能级研究宏观热力学性质的工作报道.1953年，Herzberg提出了采用相关振动光谱数据直接确定的包含多阶修正、按振动量子数作级数展开的双原子分子振动能级公式[9]，至今都还是仍被广泛采用的振动能级的重要公式，但由于展开项数多、也没有限定振动量子数的取值(项数取舍不确定)，也未见采用Herzberg振动能级研究宏观热力学性质的工作报道.3)不论是谐振子模型还是Dunham能级公式和Herzberg能级公式，如果不对振动量子数的取值有所限定，换言之振动量子数可以取无穷大(SHO就是这样的)，就意味着振动能级可以无限大.试想，当振动量子数的取值很大时就会使得振动能级大于分子的离解能De,既然分子都离解了，也就无从谈及振动能级，更无法对那些不存在的超高能级求和.反之，振动能级是分离的有限的(不能高于离解能)，有限个(客观上会出现一个最高的振动量子数vmax)非谐振且非均匀分布的振动能级完全集合{Ev,v=0,1,2,……,vmax}才是双原子分子振动能量的正确描述，它的准确性和有限性对研究宏观热力学性质至关重要[10].正因为是对有限个振动能级求和，这个求和就不能再转化为积分，既然想再获得类似于SHO模型那样的解析结果几乎是不可能了.

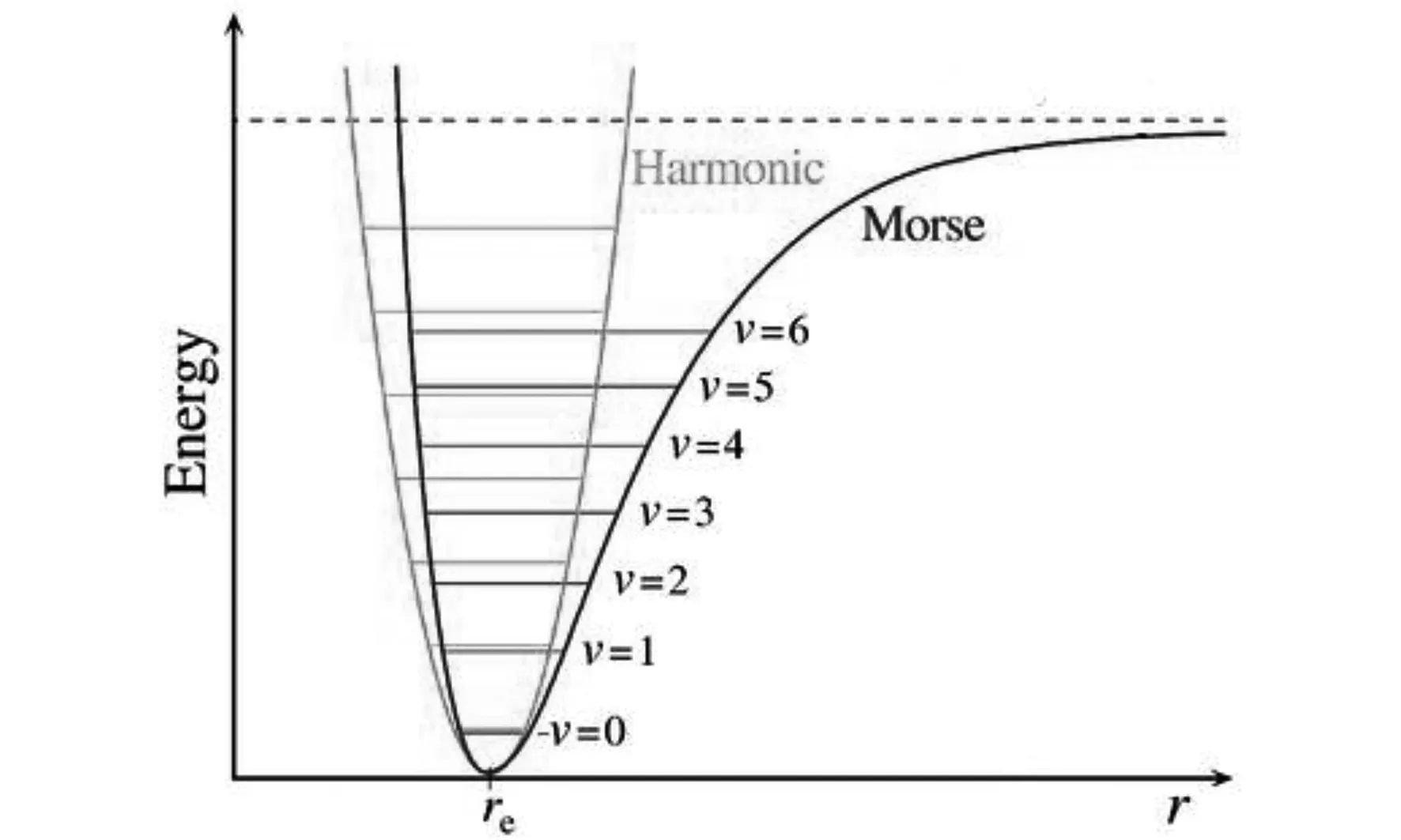
图1 双原子分子振动能级分布的大致情况Fig.1 The distribution of vibration energy levels of diatomic molecules

因此，得到双原子分子振动能级的最高振动量子数vmax和完全集{Ev,v=0,1,2, ……,vmax}是分析研究双原子分子振动热力学性质的重要基础.但要获得全套振动光谱常数却不太容易，实验方法测得的最大振动能级有的常常只是离解能De的60%左右，能超过离解能90%的已是非常难见，HCl基态算是[11]；一些理论方法(例如HF、CI方法等)得到振动能级集合，能级值往往会随着振动量子数的增高与实验值差异加大；这里采用近几年发展起来的AM方法[11]获得的振动能级完全集，就可采用量子系综统计理论分析解决了.

2 研究双原子分子振动热容量的正确方法及算例

2.1 一般理论和方法及其对比

组成宏观气体的诸多双原子分子可以处在不同电子状态的诸多振动能态，从而构成一个量子无序系统，采用量子系综理论是研究宏观双原子分子气体振动热力学性质的方法基础.虽然统计原理没有发生变化，但不应对无限能级求和，更不会过渡到积分.现将需要的统计方法和过程简述如下，并与谐振的无限振动能级的解析结果进行对比.NA是阿伏伽德罗常数，gυ是振动能态的简并度(例如，HCl分子的振动能级的简并度等于1)，β=(kT)-1，k是玻尔兹曼常数.配分函数是最基本.

SHO方法采用

(1-1)

计算结果是

(1-2)

而现在获得配分函数的依据是采用有限个振动能级求和，即

(1-3)

从这个式子看不出能够得出解析结果，后面的算例也表明只有数值结果.

内能态函数是重要的热力学函数.可直接根据配分函数与内能的关系求得SHO结果

(2-1)

现在的方法计算摩尔内能还需先采用下式计算能量的平均值

(2-2)

再由下面的式子求得内能

(2-3)

同样不会有解析结果.

振动摩尔热容量是实际可测量的重要热力学量.可直接根据配分函数与热容量的关系求得SHO结果

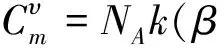
(3-1)

采用现在的方法计算时，需先用下面的公式计算出振动能级平方的平均值

(3-2)

然后采用下面的公式计算出摩尔振动热容量

(3-3)

毫无疑问，没有解析结果.

热力学系统平衡态熵是重要的标志. SHO结果可根据配分函数与熵的关系直接求得

(4-1)

而采用现在的计算方法，应按下式先求得振动量子态的几率[而不是采用(1-2)式得到的结果，更不会采用(1-3)式的结果]

pυ=e-βEυ/Q(T)

(4-2)

其中的Q(T)是采用(1-3)式得到的配分函数.再采用几率与熵的关系求得振动熵

(4-3)

肯定不会是解析结果.

2.2 HCl分子基态X1∑+的振动能谱

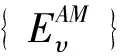
比较表1中的两组数据可见，采用AM方法得到的振动能级集合，不仅与J. A. Coxon给出的实验数据完全吻合，还给出了最高振动量子数υmax=20，补全了后面直到离解能的全部高振动能态的能级.这组振动能级完全集由低到高不间断排列的21个振动能级构成，它们成为研究双原子分子气体振动热力学性质的重要基础.

2.3 不同方法对氯化氢气体计算结果及比较

在统计物理学中，对于常见的双原子分子组成的宏观气体系统，如果温度不是很高，则可合理地认为电子基态的分子振动才对系统的振动热力学性质作出有效贡献[5].采用氯化氢分子基态的振动能谱，依据2.1节罗列的方法，就能确定氯化氢气体的振动热力学性质，包括振动热容量.为检验现在方法导致的结果Cvin,AM比SHO结果Cvin,SHO与实验数据Cv,exp符合得更好，应将两种方法导致的摩尔振动热容量结果与实验数据进行比较.但文献[13]给出的是氯化氢气体系统的定压摩尔热容量，包含了平动和转动的贡献，为将这些数据转化为摩尔振动热容量，同时减少因实际气体分子间相互作用带来的复杂性导致转换工作的复杂性，选择适合可将氯化氢气体视为理想气体的温度范围，使相关结果的误差可以很小，选择温度范围1 200 K以上是可行的，不妨给出一个温度范围，例如1 200 K～6 000 K.在这个温度范围内，平动和转动的贡献采用能均分定理的结果也是可行的.这样，氯化氢气体的摩尔振动热容量的实验数据也就形成了. 表2列出三种不同摩尔振动热容量，并计算了现在的结果和SHO结果与实验数据的相对百分偏差δnew和δSHO=(Cv,exp-Cvin,SHO)/Cv,exp.

还可以将表2中的摩尔振动热容量数据作成如图2所示.由表2和图2可见，现在的AM算法结果和SHO结果的摩尔振动热容量均小于实验结果，但SHO的结果偏离实验数据很大.在1 200 K时，AM结果相对于实验结果的百分偏差δnew是5.59%，但SHO结果相对于实验数据的δSHO为12.57%，这样的偏差是不可接受的.随着温度的增长，大约从2 600 K开始，Cv,exp、Cvin,AM和Cvin,SHO都还在增加，Cvin,AM增长仍然较快且与Cv,exp的增长趋势相似，但Cvin,SHO却增长减缓，出现了趋于极限的趋势——这正是能均分定理预计的R=8.31 J/mol.K，到了6 000 K高温，实验的Cv,exp已达10.21 J/mol.K，AM的Cvin,AM也达9.33 J/mol.K，明显高于能均分定理预计的结果8.31 J/mol.K，高出的百分比分别22.86%和12.27%，Cvin,AM与Cv,exp的相对百分偏差为8.62%，相对1 200 K时5.59%，δnew仅提高了3.03个百分点.而在6 000 K高温时，谐振子模型的结果Cvin,SHO仅为7.97 J/mol.K，与实验的Cv,exp已达10.21 J/mol.K相差很大，且与实验结果的百分偏差高达21.94%，倒是与能均分定理预计的R=8.31 J/mol.K低的不多，为-4.09%.

图2 摩尔热容量随温度的变化Fig.2 Variation of molar heat capacity with temperature

3 简短的结论和讨论

以上分析和算例表明，这里分析的方法应该更合理逻辑更严密，是对“热学”“热力学统计物理”课程相关内容的延伸和深入讨论，也是对双原子分子气体振动热容量进行分析计算的新方式，不仅具有学术价值，同样具有重要的教学意义，有助于培养学生的科学探究精神.

新的摩尔振动热容量数据明显好于无限多简谐能级求和并转化为积分的结果不止此例，我们近期的成果分析计算了SO气体的振动热容量，效果比HCl气体更好[14].但都与实验数据还有不同程度的偏差，这来自于几个原因.(1)将实际气体视为理想气体难免有些近似，从定压摩尔热容量转化成定容摩尔热容量也就有偏差，对于不同成分的双原分子气体在不同的温度压强条件下采用什么样的实际气体状态方程进而求出两个热容量之差Cp-Cv有较强的选择性，并且相关参数还会随温度变化，采用理想气体结果是简化了上述困难；(2)简单将分子的运动分解为平动、转动和振动也不尽合理，分子的转动和振动存在着耦合，然而这种耦合对振动和转动能级的定量影响未见全面准确的文献结果；(3)对于分子内部的振动，基态振动能级完全集的贡献是主要的，但当温度明显较高(例如振动特征温度的几倍)时激发态的贡献也应该考虑.上述几个问题都还值得进一步研究.