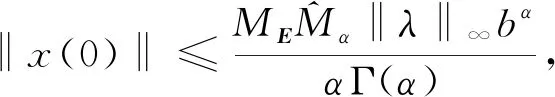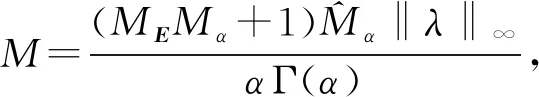分数阶非线性迭代方程的周期解

李翠英, 吴 睿, 程 毅

(1. 渤海大学 数学科学学院, 辽宁 锦州 121013； 2. 长春财经学院 数学教研部, 长春 130122)

0 引 言

目前, 关于迭代微分方程的边值、 周期问题研究已得到广泛关注. Petukhov[1]研究了如下二阶迭代微分方程周期边值问题：

得到了参数λ,α在不同范围内方程解的存在唯一性; Kaufmann[2]考虑一类二阶迭代微分方程的边值问题, 用Schauder不动点定理证明了该问题解的存在性; 文献[3-6]用不同的不动点理论(Krasnoselskii不动点定理、 Schauder不动点定理等)证明了若干类迭代微分方程周期解或拟周期解的存在唯一性. 分数阶微分方程在数学、 化学、 物理和工程等许多领域应用广泛, 但关于分数阶迭代微分方程边值、 周期问题的研究成果目前报道较少. 当非线性函数满足Lipschitz条件时, Ibrahim等[7]将整数阶的一些结果推广到分数阶迭代微分方程中. 但目前已有结果均为处理一维的迭代微分系统, 对于向量迭代方程的研究尚未见文献报道. 本文在非线性函数满足单边Lipschitz条件时, 证明一类非线性Caputo型分数阶迭代向量微分系统周期解的存在唯一性.

本文令T∶=[0,b],n为n维Euclid空间, 〈·,·〉表示n中的内积, ‖·‖表示n空间的范数. 设C(T,n)表示从T到n全体连续函数组成的空间, 其范数定义为关于分数阶微积分的基础知识可参见文献[8-9].

1 主要结果

考虑如下分数阶迭代向量微分方程：

(1)

其中:

A:n→n是一个线性算子;f:T×n×n→n是一个连续函数.

下面给出假设条件：

(H1) 设A:n→n是一个有界、 线性的正定算子, 即对任意的z∈n, 存在常数c∈+, 使得〈Az,z〉≥c‖z‖2;

(H2) 设f:T×n×n→n是一个连续函数, 且：

(i) 对任意的u,v∈n, 存在一个非负函数使得∀t∈[0,b], ‖f(t,u,v)‖≤λ(t)；

(ii) 对任意的t∈[0,b],u1,u2,v1,v2∈n存在函数使得

〈f(t,u1,v1)-f(t,u2,v2),u1-u2〉≤μ(t)‖u1-u2‖2,

其中‖μ‖∞

定理1假设条件(H1),(H2)成立, 且b大于某常数M1/(1-α), 则分数阶迭代微分系统(1)存在唯一解.

证明： 由文献[10]中推论7.1知, 问题(1)等价于如下积分迭代方程：

(2)

定义算子T1:C(T,n)→C(T,n), 且

首先， 证明解的先验有界性.

根据算子T1的定义和假设条件(H2)中(i), 可推出

其中

下面估计初值‖x(0)‖. 在式(2)中令t=b, 可得

由x(0)=x(b)和假设条件(H1)易知, 行列式|E-Eα(Abα)|≠0, 其中E表示单位矩阵. 故

根据假设条件(H2)中(i), 类似式(3), 可得

(4)

其中

ME=‖(E-Eα(Abα))-1‖.

将式(4)代入式(3), 可得

‖T1(x(t))‖≤Mbα

其次, 证明非线性算子T1是全连续算子, 从而得到解的存在性.

先证明∀x∈C(T,n),T1(x(t))∈C(T,n). 对任意的t,t+δ∈[0,b], 且δ>0, 满足

当δ→0时, 有

|T1(x(t+δ))-T1(x(t))|→0,

故T1(x(t))∈C(T,n). 取xn→x∈C(T,n), 则易推出|T1(xn)-T1(x)|→0, 从而T1:C(T,n)→C(T,n)是连续的. 根据1)中先验估计, 应用Arzela-Ascoli定理易知, 算子T1:Ω→Ω是全连续的, 其中

Ω∶={u∈C(T,n): ‖u‖C≤b+1}.

从而可将微分迭代系统(1)解的存在性转化为T1的不动点问题. 定义映射hε(x)=x-εT1(x), 其中ε∈[0,1]. 取p∉h(∂Ω), 则对任意的ε∈[0,1], 可得

其中I是恒等映射. 因此T1在Ω上存在不动点, 即x=T1(x). 从而微分迭代系统(1)至少存在一个解.

最后， 证明微分迭代系统(1)解的唯一性.

假设x1,x2∈C(T,n)是问题(1)的两个解, 对这两个解做差再与x1-x2做内积, 可得

根据假设条件(H1)和(H2)中(ii), 利用分数阶微分不等式[10], 可推出

为方便, 令S(t)=‖x1(t)-x2(t)‖2, 式(5)可简化为

DαS(t)≤2(μ(t)-c)S(t),

从而

S(t)≤S(0)Eα(2(‖μ‖∞-c)tα), ∀t∈T.

再令t=b, 得

S(b)≤S(0)Eα(2(‖μ‖∞-c)bα).

(6)

由S(t)=‖x1-x2‖2及边界条件x(b)=x(0)可知,S(b)=S(0), 整理可得

S(0){1-Eα[2(‖μ‖∞-c)bα]}≤0.

由Mittag-Leffler函数Eα(t)(t≥0)的单调性和‖μ‖∞

Eα[2(‖μ‖∞-c)bα]<1.

又由

S(0)=‖x1(0)-x2(0)‖2≥0,

可推出S(0)=0. 由式(6)知,S(t)≤0, 从而S(t)恒为0, 即x1=x2, 故迭代微分方程(1)有唯一解.