基于Harris-改进LBP的特征匹配及目标定位算法

张 震, 张照崎, 朱留存, 苗志滨, 王骥月, 李修明, 赵成龙, 张坤伦

(1. 北部湾大学 先端科学技术研究院, 广西 钦州 535001； 2. 大连理工大学-立命馆大学国际信息与软件学院, 辽宁 大连116085；3. 广西机械工业研究院有限责任公司, 广西 南宁 530007)

0 引 言

图像局部特征点在不同观察场景下不变地反映图像信息, 广泛应用于目标定位[1-2]、 图像配准与图像拼接[3-5]、 目标识别[6]和SLAM(simultaneous localization and mapping)[7-8]等领域, 已成为计算机视觉领域的研究热点. 这类方法首先对图像中显著特征进行提取, 然后利用提取特征的描述子完成两张图像间特征的匹配, 再通过特征匹配关系建立图像间的几何变换模型[8-9], 特征点检测算法大多数基于灰度的一阶或二阶导数寻找极值点. Harris等[10]提出了经典的Harris特征点检测算法, 对图像旋转、 光线变化、 噪声和视点变换不敏感; Rosten[11]提出了FAST特征点检测算法, FAST算法速度较快, 但易受噪声影响. 上述特征点检测算法都基于单一尺度, 之后研究者们提出了能适应多尺度变化的特征检测算法, 如SIFT算法[12]和SURF算法[13], SURF是SIFT的改进算法. 这类算法需要用Laplace算子或高斯差分算子构建尺度空间, 增加了计算复杂度和匹配识别的难度, 实时性较差. 文献[10-11]仅关注于特征点检测, 并未给出描述子定义算法和匹配算法. SIFT算法[12]在特征点周围取16×16的邻域, 再将邻域化为4×4个小区域, 每个小区域统计8个方向梯度, 得到128维的向量作为描述子. SURF算法[13]在特征点周围取一个具有方向的正方形邻域, 再划分为16个子区域, 每个子区域统计4个Haar小波特征, 得到64维的向量作为描述子. 上述描述子信息丰富, 但运算代价较高, 占用内存大. Calonder等[14]提出的BRIEF描述子, 极大节省了内存空间； Rublee等[15]对BRIEF描述子进行改进提出了ORB算法, 根据角度参数提取BRIEF描述子, 使其具有旋转不变性. 近几年， 相继提出了一些改进融合算法[16-23], 如文献[16]实现了Harris算法与Hist算法的融合; 文献[20]和文献[22]分别对SURF和SIFT算法做了改进， 均取得了较好的实验效果.

本文应用背景源于机器人视觉伺服抓取, 对定位精度和实时性要求较高. 经典的SIFT和SURF算法虽适应范围广、 鲁棒性好, 但实时性较差； ORB算法运行速度快, 但定位精度较低. 因此本文首先选择Harris算法[10]提取特征点; 然后采用胡矩确定特征方向, 根据特征方向获取标准化局部图像, 提取标准化局部图像的LBP特征[24]作为特征描述子； 在特征匹配阶段, 通过计算两张图像中各特征点描述子间的汉明距离实现特征匹配; 最后根据匹配结果, 定位目标在场景图像中的位置, 算法流程如图1所示.

图1 算法流程

1 Harris图像特征点提取算法

Harris算法[10]思想： 先以待检测点为中心加窗, 获取窗内像素强度; 然后移动窗口, 重新获取窗内像素强度, 计算窗口移动前后强度差. 若沿任意方向移动窗口, 强度差值均很大, 则认为待检测点为特征点.

根据上述思想可定义计算公式为

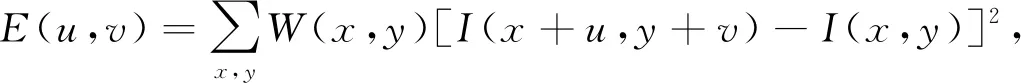
(1)

其中W(x,y)为高斯窗口,u,v为以待检测点为中心的偏移量. 由Taylor公式,

可近似为

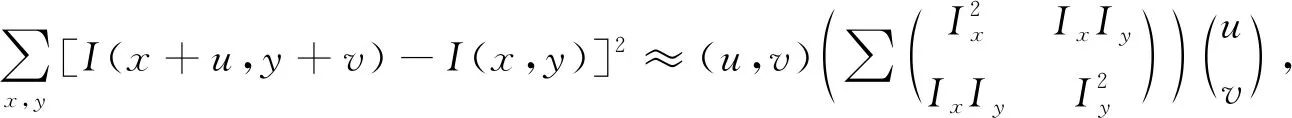
(2)

则有

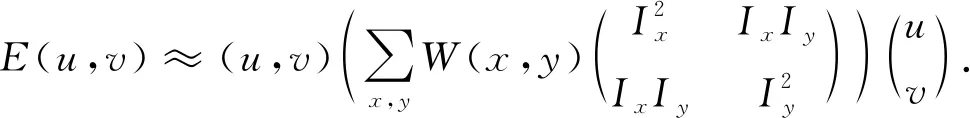
(3)

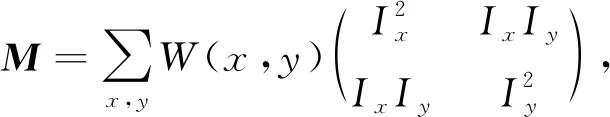
R=detM-k(trM)2.

(4)

根据经验k=0.04～0.06, 特征检测结果如图2所示. 其中： (A)为原始图像； (B)为原始图像检出的特征点； (C),(D)分别为(A)旋转10°,-10°后检出的特征点. 实验中, 将最大特征响应强度的0.1倍作为阈值. 由图2可见, Harris特征点具有旋转不变性.

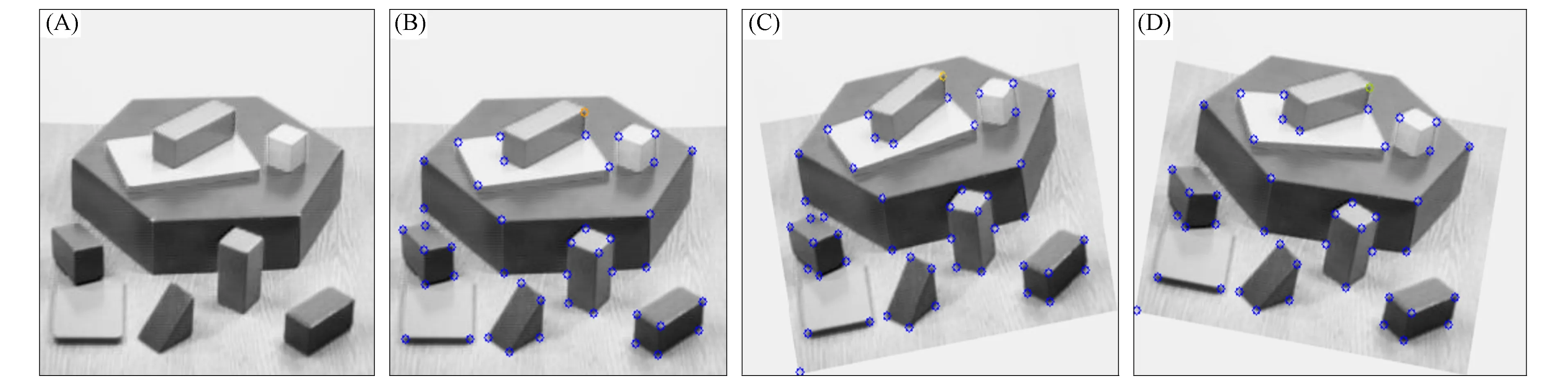
图2 Harris特征点检测结果

2 LBP的特征描述子定义

以特征点为中心截取局部图像, 计算局部图像的质心, 规定中心到质心的向量为特征点方向θ. 将局部图像旋转-θ, 得到标准化局部图像. 提取标准化局部图像的局部二值模式(LBP)特征作为特征描述子, 特征描述子生成过程如图3所示, 步骤如下.

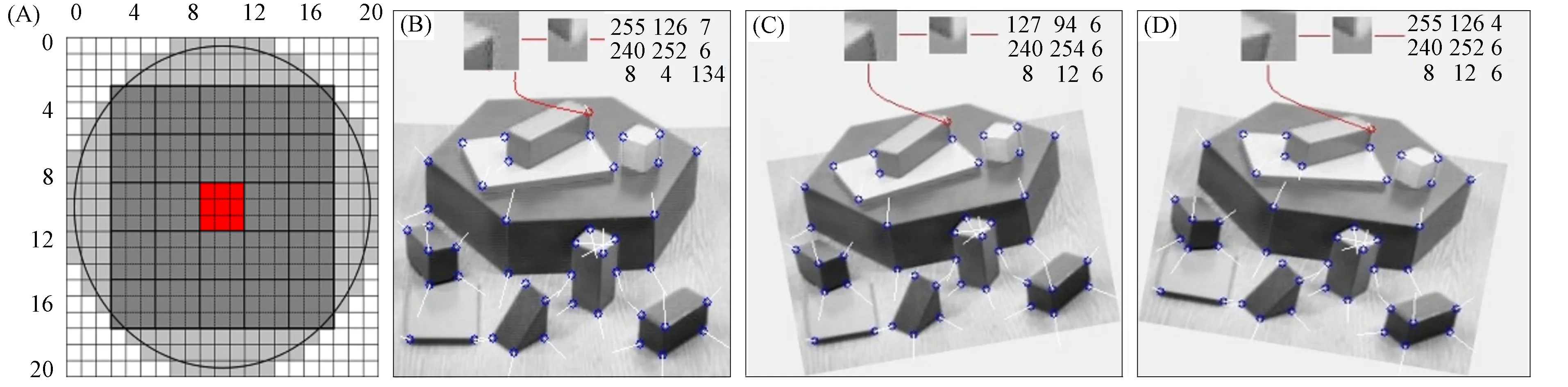
图3 特征描述子生成过程

1) 以特征点为中心截取局部图像, 本文取21×21窗口, 截取局部图像放大分别如图3(B),(C),(D)上方左侧小图所示.

2) 计算局部图像的质心(Cx,Cy)：

为保持旋转不变性, 按圆形邻域取样, 计算公式定义为

(5)

其中wx和wy为灰度图像横纵坐标,vx和vy为特征点横纵坐标,rwindow为取样窗口半径, 图3(A)浅灰色圆形区域为按式(5)设计的取样窗口, 窗口大小为21×21, 取到圆形邻域内349个点, 取样窗口大小可根据实际需要做调整.

3) 确定特征点方向θ：

各特征点方向如图3(B),(C),(D)中白线所示.

4) 将局部图像旋转-θ, 截取圆形邻域内的15×15子图像作为标准化局部图像. 15×15采样窗口如图3(A)中深灰色区域所示, 步骤1)中截取的21×21局部图像, 通过旋转-θ, 截取得到15×15标准化局部图像分别如图3(B),(C),(D)上方中间小图所示.

5) 提取标准化局部图像LBP特征作为特征描述子.

传统LBP在一个3×3的图像块中对区域进行描述, 将中心像素的灰度作为阈值, 与其8个邻域像素的灰度值对比并二值化, 小于该阈值置1, 否则置0, 然后与加权矩阵对应的值相乘, 得到8位二进制串作为LBP特征, 原理如图4所示[24], 该描述子具有速度快、 不受光照变化影响的优点.

图4 传统LBP原理

实验表明, 直接采用传统LBP提取的特征描述在特征匹配过程中算法性能较差, 这是因为提取的特征点位置难免有误差, 且特征点坐标位置是浮点型, 在取整过程中也存在误差, 这种误差的累计对特征匹配影响较大. 因此, 本文对传统LBP算法进行改进, 方法如图3(A)中深灰色区域粗实线所示, 将15×15标准化局部图像分成5×5个子块, 将每个子块(3×3个像素)作为一个整体, 然后进行LBP特征提取, 该步骤采用积分图像法提高速度. 针对5×5个子块, 可提取到3×3个LBP特征作为特征点的描述子, 如图3(B),(C),(D)上方矩阵所示. 改进后的LBP算法可削弱特征点定位误差的影响, 使匹配过程中算法的稳定性得到改善.

3 特征匹配与目标定位算法

特征匹配的依据是特征点描述子间的相似度, 本文采用汉明距离作为度量标准, 即待匹配两个描述子间9个二进制串中不相同位的个数.

特征匹配步骤如下：

1) 选择标准图像中的任意描述子G[m];

2) 在场景图描述子中寻找G′[n], 使得d(G[m],G′[n])最小;

3) 若d(G[m],G′[n])<τ, 则认为标准图像特征点m与场景图像特征点n匹配(τ为阈值).

特征匹配结果如图5所示, 每条连线对应的两点为匹配的特征点.

目标定位过程如下：

1) 寻找两组匹配特征点间的变换关系, 即估计归一化单应性矩阵：

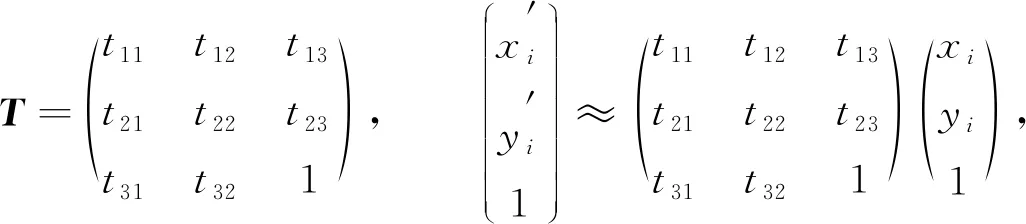
(6)

2) 根据标准图像4个顶点坐标, 利用式(6)计算对应场景图像4个顶点的坐标, 从而定位目标. 目标定位结果如图5所示, 红色框定位了标准图像在场景图像中位置, 利用式(6)可计算标准图像每个像素点在目标图像中的位置.

图5 旋转10°(A)和-10°(B)特征匹配及目标定位结果

4 实验结果对比分析

图6～图9分别为本文算法与SIFT[12],SURF[13],ORB[15]算法的匹配及定位效果对比. 图6～图9分别采用Lena图像、 Barche图像、 Goldhill图像和Barbara图像作为标准图像, 各自旋转10°后作为场景图像. 通过调整算法参数, 4种算法特征匹配数量基本相同. 观察发现, SIFT及本文算法定位精度差异较小, 但均好于SURF和ORB算法. 下面以图7中Barche图像为例进行实验数据对比, 衡量4种算法的运行速度和定位精度. 定位精度实验中, 考虑到机器人视觉伺服抓取过程, 相机位置固定, 工件图像只发生位置偏移和旋转变化, 不存在尺度变化和仿射变换, 因此主要对平移和旋转误差进行对比.

图6 不同算法的Lena图像匹配及定位效果对比

图7 不同算法的Barche图像匹配及定位效果对比

实验环境： 电脑主频3.6 GHz, 内存16 GB, 操作系统Win10 64位, 开发平台VSC++. 其中, SIFT,SURF,ORB算法实现调用了OPENCV库函数. 由于SIFT,SURF算法已申请专利, 不能在RELEASE模式下运行, 为具可比性, 4种算法均在DEBUG模式运行. 表1为Barche图像各角度下不同算法定位过程运行时间的对比.

表1 不同算法运行时间(ms)对比

由表1可见: ORB算法耗时最少； 本文算法次之, 约为ORB算法的3倍； SURF和SIFT算法实时性较差, 耗时约为ORB算法的9倍和15倍.

平移误差定义为： 定位中估计的4个边界顶点坐标与场景中对应4个实际边界顶点坐标之间距离的最大值. 表2为各角度下不同算法定位过程平移误差的对比. 由表2可见： SIFT算法精度最高, 误差均值为0.52, 误差最大值为0.77； 本文算法略差于SIFT算法, 误差均值为0.63, 误差最大值为1.15； SURF算法误差均值为1.18, 误差最大值为5.60； ORB算法精度最差, 误差均值为3.31, 误差最大值为7.22.

图8 不同算法的Goldhill图像匹配及定位效果对比

图9 不同算法的Barbara图像匹配及定位效果对比

旋转误差定义为： 定位中估计的4条边界线与场景对应4条实际边界线角度偏差绝对值的最大值. 表3为各角度下不同算法定位过程旋转误差的对比. 由表3可见： SIFT算法精度最高, 误差均值为0.02, 误差最大值为0.04； 本文算法精度次之, 误差均值为0.15, 误差最大值为0.25； SURF算法误差均值为0.44, 误差最大值为1.05； ORB算法精度最差, 误差均值为0.50, 误差最大值为1.84.

实验结果表明： 本文算法定位精度略差于SIFT算法, 明显优于SURF和ORB算法； 定位速度慢于ORB算法, 远好于SIFT和SURF算法, 能满足实时性要求. 基于本文应用背景, 本文算法综合表现最好, 已应用于5轴机器人伺服定位抓取系统, 经过近30 d实际验证表现出良好的稳定性.

表2 不同算法平移误差(像素)对比

表3 不同算法旋转误差(°)对比

综上所述, 本文算法通过改进传统LBP定义的特征描述子, 具有定位精度高、 运行速度快、 鲁棒性好、 不受光照变化影响的优点. 但在特征提取过程中保留了Harris算法对尺度变化敏感的不足, 在描述子生成过程中旋转子图像步骤耗时较多.