似星树与路的乘积图的任意可分性

张盼盼, 刘凤霞, 孟吉翔

(新疆大学 数学与系统科学学院, 乌鲁木齐 830046)

1 引言与预备知识

设图G=(V,E)是阶为n的简单图, 正整数序列λ=(λ1,λ2,…,λp)是一个非递减序列. 如果λ1+λ2+…+λp=n, 则称λ是G的可允许序列. 如果λ是一个可允许序列, 且存在对点集V的一个划分(V1,V2,…,Vp), 使得每个Vi导出一个阶为λi的G的连通子图, 则称λ是G的可实现序列, 且(V1,V2,…,Vp)是序列λ在G中的实现, 每个子图G[Vi]称为图G的λi分支. 如果每个可允许序列都是可实现的, 则称G是任意可分图(简称AP图或AVD图)[1]. 如果图G含一条Hamilton路, 则称图G为可迹图. 显然, 每个可迹图都是任意可分图. 当图G的阶为偶数时,G有完美匹配等价于序列(2,2,…,2)是G的可实现序列； 当图G的阶为奇数时,G有几乎完美匹配等价于序列(1,2,…,2)是G的可实现序列. 因此, 任意可分图一定有完美匹配或几乎完美匹配, 从而一个图有完美匹配或者几乎完美匹配的必要条件是该图为任意可分图.

如果图G的生成树是任意可分图, 则图G是任意可分图. Horňk等[2]证明了如果树T是任意可分的, 则T的最大度至多为6, 并且提出了任意可分树的最大度至多为4的猜想. 该猜想被Barth等[3]证明, 得到了任意可分树的最大度至多为4, 且每个4度顶点与一个叶子点相邻的结论. Cichacz等[4]刻画了4个叶子点的毛毛虫树的任意可分性, 并展示了最大度为3或4的两类任意可分树. Marczyk[5]证明了对阶为n的连通图G, 当独立数至多为n/2, 且任意一对不相邻顶点的度和至少为n-3时, 图G是任意可分图或者同构于两个例外图. Horňk等[6]证明了对阶数n≥20的连通图G, 任意两个不相邻顶点的度和至少为n-5, 则G有完美匹配或几乎完美匹配. Baudon等[7]提出了任意可分图和可迹图的笛卡尔积图是任意可分图的猜想, 证明了可迹图的顶点数至多为4时猜想成立, 并证明了当两个任意可分图中至少有一个阶数至多为4时, 这两个任意可分图的笛卡尔积图也是任意可分图. 文献[8]证明了树T的最大度至多为l+1时, 如果T中有一条包含所有(l+1)度顶点的路, 则T□Cl是任意可分图. 此外, 文献[9-11]研究了树的笛卡尔积图的相关性质.

本文将两个图G和H的乘积图记为G▷◁H, 其顶点集

V(G▷◁H)={(g,h)|g∈V(G)且h∈V(H)},

边集

E(G▷◁H)={(g,h)(g′,h′)|gg′∈E(G)且hh′∈E(H)或gg′∈E(G)且h=h′}.

用S=S(a1,a2,…,at,b1,b2,…,bs)表示最大度为t+s的似星树, 设d(v)=t+s, 则

S-{v}=Pa1∪Pa2∪…∪Pat∪Pb1∪Pb2∪…∪Pbs,

其中Pai=vi1vi2…viai,Pbj=v(t+j)1v(t+j)2…v(t+j)bj, 且ai(1≤i≤t)是奇数,bj(1≤j≤s)是偶数,

本文给出在t和s的不同取值下, 乘积图S▷◁Pl的任意可分性.

2 主要结果

设S=S(a1,a2,…,at,b1,b2,…,bs)是最大度为t+s的似星树, 假设t+s≥2. 设G=S▷◁Pl, 其中|Pl|=l≥2, 图Sp是S在G中的第p个拷贝, 其对应的点集为

其中vp是Sp的最大度点. 似星树S(a,b,c)是阶为1+a+b+c, 由一个3度顶点连接3条长分别为a,b,c的不交路的图. 本文将序列(λ1,…,λ1,…,λp,…,λp)记为((λ1)k1,…,(λp)kp), 对i∈{1,2,…,p},λi出现ki次. 两个正整数a和b的最大公因子记为gcd(a,b).

命题1对于图G及其可允许序列λ=(λ1,λ2,…,λp), 存在(V1,V2,…,Vm), 满足

|V1|=λ1, |V2|=λ2, …, |Vm|=λm,

且G[Vj]连通, 其中1≤j≤m, 如果

V-V1-V2-…-Vm=V0,

G[V0]有一条Hamilton路, 则必存在Vm+1,Vm+2,…,Vp, 满足|Vi|=λi且G[Vi]连通, 其中m+1≤i≤p. 因此, 图G的可允许序列λ=(λ1,λ2,…,λp)是可实现的.

引理1(Tutte’s定理)[12]设图G是阶为偶数的连通图, 则图G有完美匹配当且仅当对所有的点子集S⊂V, 均有o(G-S)≤|S|.

引理2[13]设图G是阶为奇数的连通图, 则图G有几乎完美匹配当且仅当对所有的点子集S⊂V, 均有o(G-S)≤|S|+1.

引理3[1,14]设图G是似星树S(1,a,b), 且1≤a≤b, 则图G是任意可分图当且仅当

gcd(a+1,b+1)=1.

定理1设S=S(a1,a2,…,at,b1,b2,…,bs)是似星树, 其中t≥2, 则图S▷◁Pl不是任意可分图.

证明: 设G=S▷◁Pl, 为证明图G不是任意可分图, 只需找到一个不可实现的序列, 下面证明图G不含完美匹配或几乎完美匹配.

取G的独立集

图G-I的奇分支数为o(G-I), 如图1(A)所示. 设m=a1+a2+…+at,Si是S在图G中的第i个拷贝, 则有

因为t≥2, 则o(G-I)-|I|≥2. 由引理1和引理2知, 图G不含完美匹配或几乎完美匹配. 因此, 图G不是任意可分图.

定理2设S=S(a1,a2,…,at,b1,b2,…,bs)是似星树, 其中t=0, 则图S▷◁Pl不是任意可分图.

证明: 设G=S▷◁Pl, 由t+s≥2,t=0知s≥2, 与定理1的证明类似. 令图G的独立集

o(G-I)是图G-I的奇分支数, 如图1(B)所示. 设m=b1+b2+…+bs,Si是S在图G中的第i个拷贝. 显然,G-I是孤立点, 则有

由引理1和引理2知, 图G不含完美匹配或几乎完美匹配. 因此, 图G不是任意可分图.

定理1和定理2分别讨论了t≥2和t=0的情形, 下面讨论t=1的情形.

定理3设S=S(a1,a2,…,at,b1,b2,…,bs)是似星树, 其中t=1,s=1, 则图S▷◁Pl是任意可分图.

图1 图G的拷贝Si

证明: 设G=S▷◁Pl, 当l为偶数时, 可找到图G中的一条Hamilton路P, 如图2所示, 即

图2 图S(a1,b1)▷◁Pl(l为偶数)

当l为奇数时, 同理可找到图G中的一条Hamilton路. 因此, 图G是任意可分图.

定理4设S=S(a1,a2,…,at,b1,b2,…,bs)是似星树, 其中t=1,s=2, 即S=S(a1,b1,b2), 则图S▷◁Pl是任意可分图.

证明: 下面仅讨论l为奇数的情形, 当l为偶数时同理可证. 令

1) 如图3所示,a1=1. 此时, 设

则

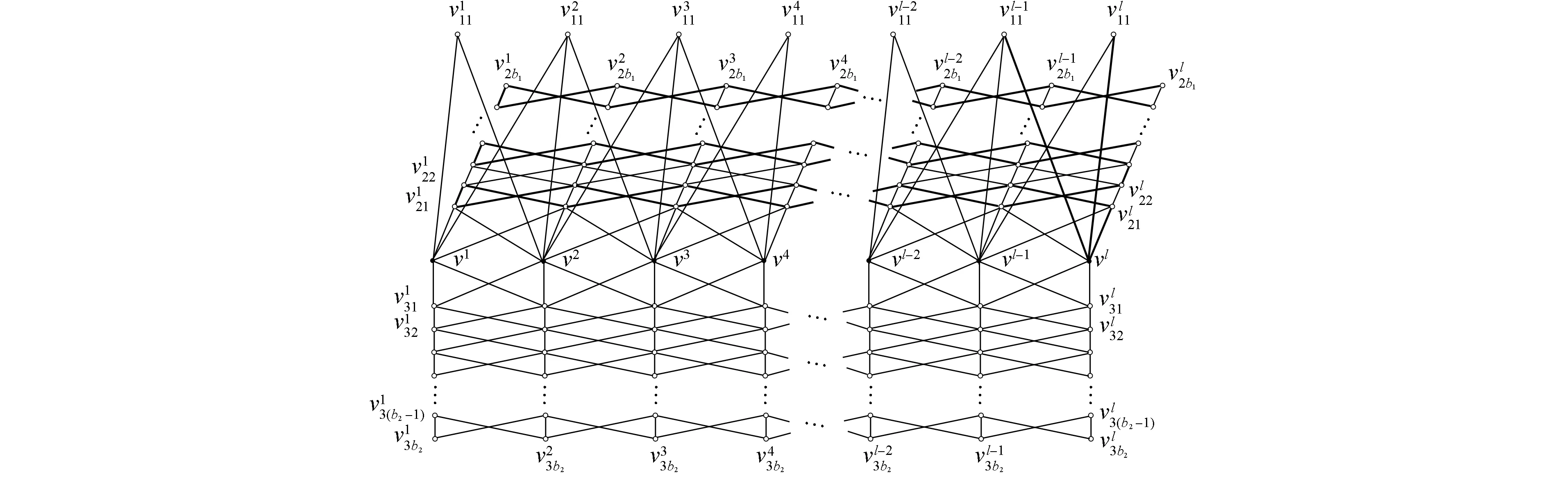
图3 图S(1,b1,b2)▷◁Pl

① 当r=1时, 令Vr={vl-1}.

2) 如图4所示,a1≥3. 此时, 令

图4 图S(a1,b1,b2)▷◁Pl

gcd(2,b1l+(a1-1)(l-1)+1)=1.

由引理3, 似星树S(1,1,b1l+(a1-1)(l-1))是任意可分图. 因此, 序列λ在图G中是可实现的.

因此, 序列λ是图G的可实现序列.

定理5设S=S(a1,a2,…,at,b1,b2,…,bs)是似星树, 其中t=1,s≥3, 且Δ(S)≥l+2. 如果b1=b2=…=bs, 则图S▷◁Pl不是任意可分图.

证明: 设G=S▷◁Pl, |G|=n,Δ(S)=k. 令q=b1=b2=…=bs且b=ql, 则

n=(k-1)b+(a1+1)l.

考虑到图G-{v1,v2,…,vl}连通分支的阶为a1l和b, 下面分两种情形讨论.

1) 若a1

c=n-l(b+1)=(k-1)b+a1l-bl>a1l.

若λ是G的可实现序列, 则每个b+1分支必须包含一个点vi,i∈{1,2,…,l}. 因为c≥a1l+1, 故c分支必包含一个点vi,i∈{1,2,…,l}, 共需(l+1)个点, 与l=|{vi|i=1,2,…,l}|矛盾.

2) 若a1>b1, 则如果k=l+2, 可考虑G的可允许序列λ=((b+1)l,a1l+1,c), 其中c=b-1. 如果k>l+2, 可考虑G的可允许序列λ=((b+1)l+1,a1l+1,c), 其中c=(k-l-2)b-2.

在这两种情形下, 每个b+1分支必包含一个点vi,i∈{1,2,…,l}, 每个a1l+1分支也必包含一个点vi,i∈{1,2,…,l}, 与l=|{vi|i=1,2,…,l}|矛盾, 故λ不是G的可实现序列, 图S▷◁Pl不是任意可分图.