一种求解复杂优化问题的快速遗传算法算子

裴 莹, 苏 山, 付加胜, 韩霄松

(1. 长春财经学院 信息工程学院, 长春 130122； 2. 吉林大学 计算机科学与技术学院, 符号计算与知识工程教育部重点实验室, 长春 130012； 3. 中国石油集团工程技术研究院有限公司 钻井工艺研究所, 北京102206)

遗传算法(genetic algorithm, GA)是一种启发式的搜索策略, 通过模拟生物进化论的自然选择和遗传学机理搜索最优解[1]. Holland[1]提出的模式定理和积木块假说为GA提供了理论依据. GA源于一组候选解决方案的种群, 其中每个候选解决方案是该种群的个体或染色体, 染色体通过基因进行编码得到. 根据优胜劣汰原则, 将种群中的染色体通过交叉、 选择和变异等操作, 产生含有更好解决方案的新群体. 产生的新种群每一代都不弱于前一代, 直到满足进化终止条件, 最优个体被解码并被用于问题的最佳解决方案. GA由于结构简单并具有强大的全局搜索能力, 广泛应用于机器人与自动控制[2]、 交通调度[3]、 车间调度[4]和神经网络训练[5]等领域.

分析表明, GA的运行依赖于大规模的个体适应度计算, 当适应度计算较复杂时, GA寻优过程十分耗时. 很多优化问题(尤其在工业领域)需要优化的参数维度通常较高(high-dimensional), 适应度计算复杂(expensive-computationally), 且有些优化问题无法得到数学解析式, 解决方案的优劣依赖于其他工具(black-box), 这类优化问题的优化较困难, 被称为HEB问题[6]. 针对HEB问题, 目前已有很多研究成果： Branke等[7]利用邻近个体的适应度值通过插值和回归估计个体的适应度, 取得了较好的实验结果； Regis[8-11]将代理模型融合到粒子群等算法中, 得到了良好的实验结果, 并将其应用到地下水除污等实际问题中[12-13]; 刘全等[14]提出了一种双精英联合遗传算法避免了GA的早熟问题, 提高了收敛速度； Yoel[15-16]利用分类器预测能导致适应度计算失败的参数组合, 通过筛选参数组合达到提升算法效率的目的； Han等[17]提出的EGA算法(efficient GA)中构建了聚类算法和模式理论的适应度估计策略, 通过减少适应度计算次数有效加速GA, 实验结果表明, EGA算法在保证速度的同时具有与经典GA相似的优化精度, 并将该算法扩展到粒子群算法中, 取得了较好的效果[18].

上述研究大多数采用代理模型策略替代适应度函数, 从而通过减少调用真实适应度函数方法加快寻优速度. 通过提高算法收敛速度是解决HEB问题的另一种思路, 文献[19]提出的基于全局最优预测的自适应变异粒子群优化算法(global prediction-based adaptive mutation PSO, GPAM-PSO), 利用主成分分析(PCA)算法对群体进行降维, 并在低维空间拟合曲面寻找更优粒子引导群体进化, 算法引入了自适应的变异策略避免陷入局部极值, 实验结果表明, GPAM-PSO算法相比于经典粒子群算法可以更快地收敛. 本文将GPAM-PSO的核心思想扩展到GA, 提出通过聚集算子(aggregation operator)在GA进化中发现更优的个体引导种群进化, 从而使GA可以快速收敛.

1 聚集算子

对GA的算法流程分析表明, 种群中新个体的产生全部来源于交叉和变异操作, 其中绝大多数来源于交叉操作, 但两两交叉不是每次都产生更好的个体, 因而会使算法收敛速度缓慢, 且具有随机性, 易产生早熟现象. 为解决该问题, 本文在GA中引入聚集算子, 该算子首先采用聚类方法对群体进行划分, 然后对聚类后的每一簇个体用PCA算法进行降维, 再采用最小二乘法对降维后的种群个体分布进行拟合, 并求出低维空间下的优势个体, 最后将该个体还原到初始空间保存到下一代种群. 聚集算子流程如图1所示.

图1 聚集算子流程

图2对聚集算子的有效性进行了解释, 其中红色五角星位置为最优位置, 蓝色三角星为每一代聚集算子产生的优势染色体位置, 优势染色体将引导种群向最优值靠近, 从而加速了搜索方法. 聚集算子主要包括GA种群划分、 种群降维、 低维空间下种群分布拟合、 优势染色体发现和优势染色体返回五部分.

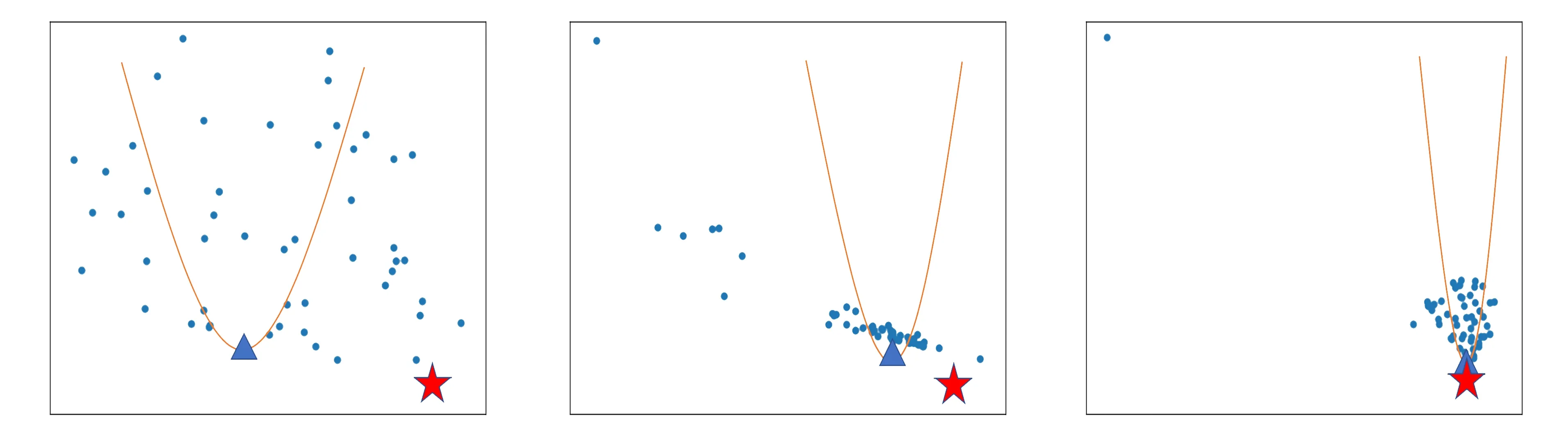
图2 聚集算子特征

1.1 基于AP聚类的GA种群划分

GPAM-PSO算法中每次迭代仅生成一个优势个体, PSO算法的特点为保证所有粒子都会向优势个体聚集. 但GA中如果每次进化仅产生一个优势个体, 由于GA选择操作的随机性, 该个体不一定发挥作用, 为更大程度地利用优势个体, 在GA中提出的聚集算子每次迭代将产生多个优势个体. 方法是对GA临时种群进行聚类, 每个聚簇产生一个优势个体. 本文采用AP(affinity propagation)聚类对GA种群进行划分, 基于数据点间的“信息传递”进行聚簇, 每次迭代计算并传播每个数据点的吸引度和归属度[20], 计算公式为

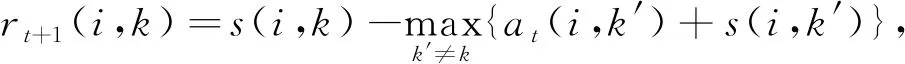
(1)

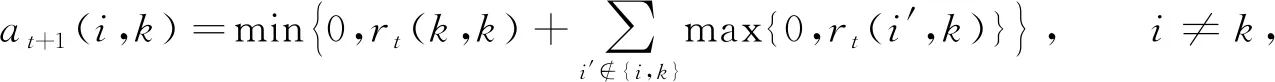
(2)

(3)

吸引度r(i,j)由数据点i传向候选聚类中心j, 表示点j作为点i聚类中心的累积证据； 归属度a(i,j)由候选聚类中心j传向数据点i, 表示以点j作为聚类中心的聚类包含点i的累积证据；s表示两个数据点的相似性, 一般采用负的欧氏距离. 对上述步骤进行迭代, 若归属度和吸引度保持不变或者在一个小范围内振荡, 或者算法执行超过设定的迭代次数则算法结束. 为避免振荡, AP聚类更新信息时引入了衰减系数λ, 则吸引度和归属度公式更新为

rt+1(i,k)←(1-λ)rt+1(i,k)+λrt(i,k),

(4)

at+1(i,k)←(1-λ)at+1(i,k)+λat(i,k).

(5)

相比于传统聚类算法, AP聚类可根据数据分布自动确定聚类数目, 聚类中心是真实存在的点, 结果稳定且误差小. 这些特征十分适合对没有先验信息的GA种群进行聚类, 可根据当前种群结构自适应地聚类从而达到有效划分的目的. 在GA迭代过程中, 为保持聚簇内元素数量, 当元素数小于6时, 合并除主要聚簇外的聚簇. 这种处理方法的优点是: 在大型聚簇中进行了开发操作, 在多个小型聚簇上进行探索操作, 提高收敛速度的同时避免了早熟.

1.2 基于PCA的GA种群降维

主成分分析(principal component analysis, PCA)是经典的无监督降维算法, 通过正交变换将数据特征转换为一组线性不相关的新特征, 选择新特征在更小维度下展示数据的特征. 方法是对数据进行中心化后的协方差矩阵进行奇异值(SVD)分解, 原始数据通过SVD分解的旋转矩阵得到新特征, 然后根据特征值大小选择主成分进行降维, 利用旋转矩阵的转置可从新特征返回到原始数据. PCA是最简单有效的降维方法之一, 且实现简单、 算法复杂度低, 用在聚集算子中不会给算法带来额外的开销. 本文提出的聚集算子采用PCA可快速对种群进行降维, 在低维空间中可采用简单的回归算法拟合种群结构, 利用拟合曲面快速发现优势个体, 并利用PCA将优势染色体返回到原始空间.

1.3 基于WLS的GA种群结构拟合及优势个体发现

最小二乘法(ordinary least squares, OLS)是一种解决数学优化问题的有效方法, 其计算方式是利用最小误差平方和找到最符合所有数据的曲线或曲面. 为能在本文提出的聚集算子中快速发现优势个体, 本文利用OLS在低维空间拟合一个二次曲面, 从而利用二次函数的求解公式得到曲面极值位置的数学解析解. 为提高OLS泛化能力, 本文采用加权最小二乘法(weighted OLS, WLS), WLS给每个观测值分配一个反映测量不确定度的权重wi, 其最小二乘准则为

(6)

其中ε表示误差, 即要最小化的量, {Xi,Yi}为观测量,a和b分别为回归线的截距和斜率.

算法1融合聚集算子的遗传算法(genetic algorithm with aggregation operator, aGA).

步骤1) 初始化： 指定AP聚类P值, 设置PCA特征选择数目n或特征累计占比阈值θ, 进化代数计数器t=0, 设置最大进化代数T及适应度评价函数f, 函数随机生成M个染色体作为初始种群P(0)；

步骤2) 个体评价： 利用适应度函数f计算种群P(t)中每个染色体的适应度；

步骤3) 传统算子作用在种群上；

① 选择运算： 将选择算子作用于种群；

② 交叉运算： 将交叉算子作用于种群；

③ 变异运算： 将变异算子作用于种群；

步骤4) 种群P(t)经过选择、 交叉、 变异运算后得到临时种群P(t0)；

步骤5) 聚集算子作用在临时种群P(t0), 合并较小聚簇；

① AP聚类算法将种群P(t0)划分成N簇；

② PCA算法对每簇进行降维, 保存n个最大成分, 或者累加占比超过θ的n个主成分；

③ WLS算法将每簇拟合成二次曲面并求得极值, 发现优势染色体；

④ 将N个优势染色体利用PCA旋转矩阵返回原始空间加入临时种群P(t0)；

步骤6) 选择算子从临时种群P(t0)选择个体产生新种群P(t+1)；

步骤7) 终止条件判断： 若t=T, 则以进化过程中所得到的具有最大适应度个体作为最优解输出, 终止计算.

2 数值实验

2.1 实验设计

为验证算法聚集算子的效率, 本文选取10个Benchmark函数和经典GA对比, 包括3个单峰函数和7个多峰函数, 测试函数信息列于表1. 算法实验的种群大小为100, 最大迭代次数为50次, 优化参数采用30维. 为对比方便, 将适应度规约为0～100.

2.2 实验结果分析

针对表1中的每个测试函数, aGA和GA分别运行10次, 每种算法的平均迭代曲线如图3所示, 平均最优适应度和收敛位置列于表2.

表1 测试函数

表2 测试函数结果

图3 测试函数迭代曲线

由图3和表2可见: 在单峰函数实验中, aGA都快速达到近似最优解, GA缓慢达到最优解； 在多峰函数中, 3个函数Weierstrass,Ackley,Rastrigin在aGA中不仅快速收敛, 而且最优值优于GA, 其他函数虽然最终收敛值未超过GA, 但优化精度接近, 除Schwfel函数外收敛速度明显提升. 尽管由于引入聚集算子使每次迭代比较耗时, 但聚集算子可使GA迭代几次后快速收敛. 实验结果表明, 当适应度计算十分耗时时, 如当适应度计算超过10 ms时或将算法终止条件设为连续5代适应度不发生改变时, aGA的优势明显.

综上所述, 本文在遗传算法中引入了聚集算子, 该算子利用AP聚类对群体进行划分后, 通过PCA对每一聚簇进行降维, 在低维空间利用加权最小二乘法将聚簇分布拟合成二次曲面, 并将求得的极值作为优势染色体返回到原始群体, 从而引导遗传算法快速收敛. 10个标准测试函数的测试结果证明了该算法的有效性.