基于真实问题解决的教学策略——以“带电粒子在磁场中运动的放缩圆模型”微专题为例

林晓琦

（福州高级中学，福建福州 350007）

发展核心素养，倡导学生在面对各种复杂多样的真实问题情境中，能够合理有效地运用科学的思维方式与方法，有效整合已有的知识与经验，运用相关学科能力，创造性地分析问题、解决问题。［1］真实具体、富有价值的问题情境，是学生学科核心素养形成和发展的重要载体，也为学生学科核心素养提供了真实表现的机会。［2］

运用物理知识解决真实问题能力的高低，取决于学生将问题情境与所学知识联系的水平。将情境与知识联系过程中，能否把描述情境的文字、数据、图表等形式的信息，转化为物理表述，能否从复杂的情境中抓住主要因素，抽象出物理模型，转化为物理问题解决是物理学科核心素养发展水平的重要标志。

在实际解决问题中，由于有的学生模型意识不强，建模能力不足，导致在解决难度稍大的新情境和实际问题时，无法正确把握事物本质、构建合适的物理模型。这就需要教师站在学生学习和成长的角度，通过教学设计，选择和确定适宜的真实问题情境，让学生有解决实际问题的经历和体悟，促进学生与经验知识的深度互动，主动建构认识，最终转化为学生的素养发展。

带电粒子在磁场中的运动是历年高考考查的热点，可以很好地考查学生逻辑推理、模型建构、质疑创新等科学思维。以《带电粒子在磁场中运动的放缩圆模型》微专题为例，教师通过设计一系列真实问题，引导学生经历放缩圆模型的建构过程，让学生在反思模型建构中，感悟所用的思维方式与方法，理解模型适用的条件，运用模型解决实际问题，促进学生核心素养的发展。

一、创设问题情境，经历模型建构

问题是思维的源泉。通过情境问题，将知识内容转化为学习任务，形成驱动性任务，引导学生主动学习，在前概念基础上不断探究，进行知识建构。

［问题1］在磁感应强度为B的匀强磁场中的O点有一粒子源，能够向外发射质量为m、带电量为q（q＜0）的带电粒子（不计重力）以速度v0垂直进入磁场（如图1所示），请画出粒子在磁场中的运动轨迹。

［问题2］保持粒子入射方向不变，改变速度大小，请画出速度大小分别为2v0，3v0，4v0，5v0时，粒子的运动轨迹。

设计意图：在实际问题解决中，由于有的学生缺乏规范作图意识，不重视精准建模，漫无目的地试错，甚至不画粒子的运动轨迹，效率低下，导致遇到稍微复杂点的问题往往不知从何入手。通过有效问题的导引，让学生经历利用尺规，规范作出带电粒子运动轨迹的过程，感悟确定轨迹圆圆心与半径的方法。以入射速度为v0的粒子运动轨迹为基准，按照比例关系，准确画出其他几个轨迹圆（如图2所示），培养学生规范作图的意识，引导准确建模。

二、感悟模型特点，理解模型条件

实际问题情境中的有界磁场形状各异，有的学生由于未能真正理解掌握模型本质，反被形状各异的边界所迷惑，导致遇到新情境问题时，无法将其转化为所学的经典物理模型进行分析、解决问题。让学生反思模型建构、体悟所用的思维方式与方法的过程，就是让他们与正在学习的内容之间进行深度交流，建立一种紧密的灵魂联系。只有这样，事物的本质才会显现，准确理解模型条件。

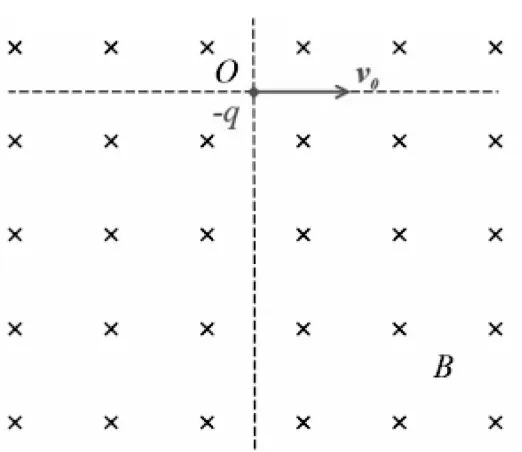
图1

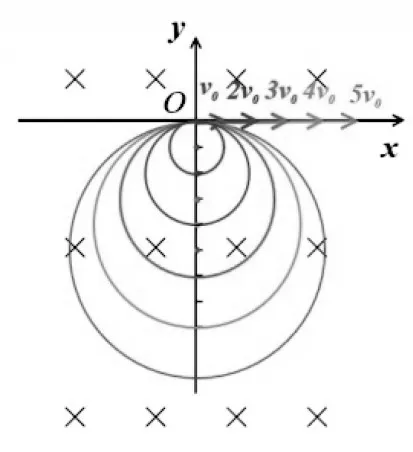
图2

［问题3］观察、总结轨迹圆和圆心分布特点。

设计意图：学生通过观察，总结轨迹圆和圆心分布特点：①轨迹圆内切于入射点；②圆心均分布在入射速度的垂线上；③入射速度增大，轨迹圆半径增大，但圆周运动的周期相同。学生在反思感悟中，理解模型条件——入射速度方向一定、大小各异。同时，他们还充分感受到物理模型之美，并给这种模型一个形象的名字——放缩圆。

三、运用变式问题，突出模型本质

通过设置多层次的变式问题，突出其中不变因素，有利于学生形成对问题多角度、全方位的认识，深刻理解模型本质。这需要学生清楚问题情境下他们已有的知识，并在问题情境中主动应用所掌握的知识，运用特定的程序和方法解决问题。

［问题4］如图3所示，若带电粒子与y轴成θ 角垂直射入匀强磁场后，从y轴射出磁场，求粒子在磁场中运动的时间。

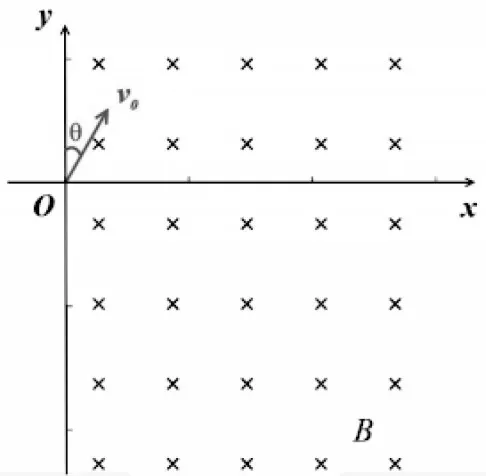
图3

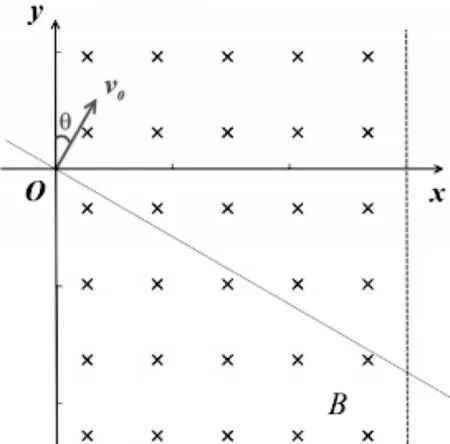
图4

设计意图：从无界磁场变式为直线边界磁场，粒子与边界成一定夹角射入，分析解决问题的思路和方法还是定圆心、找半径、画轨迹。找到运动轨迹对应的圆心角，即可求得运动时间。进一步分析发现，无论粒子入射速度多大，只要是从同一边界进、出磁场的，运动轨迹对应的圆心角相等，运动时间也相同。

变式1：若在x=d处存在磁场的右边界（如图4所示），求从右边界射出磁场的粒子入射速度v0的取值范围。

带电粒子入射速度越大，轨迹半径越大，恰好不从右边界射出的临界轨迹的确定是解决问题的关键。鼓励学生多画几条半径不同的运动轨迹，有的从左边界射出磁场，有的从右边界射出磁场。再借助动画模拟（如图5），将抽象的运动过程形象化，让学生具身感受速度越大、半径越大、轨迹圆越来越大的逐渐放大过程，从而确定恰好不从右边界射出的临界轨迹是与右边界相切的（如图5所示）。再利用牛顿运动定律，结合几何关系解决问题。

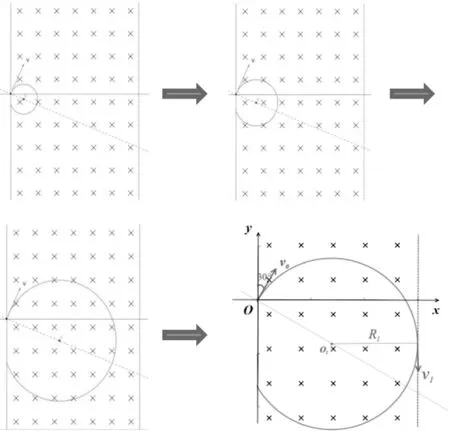
图5

变式2：若在y=处存在磁场的上边界（如图6所示），且θ=30°，求从右边界射出的粒子入射速度v0的取值范围。

在变式1的基础上多了一个上边界，需要学生全面考虑问题，只有不从上边界射出的粒子，才有可能从右边界射出磁场，恰好不从上边界射出磁场的临界轨迹（如图7所示），从而确定临界条件。

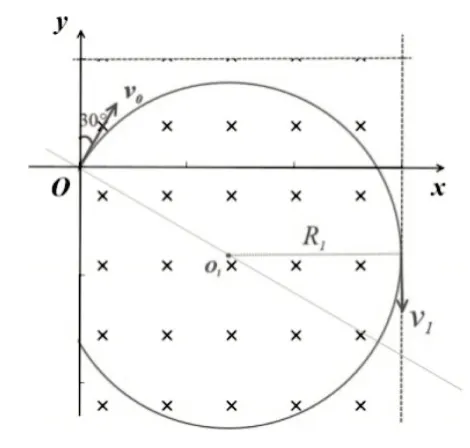
图6

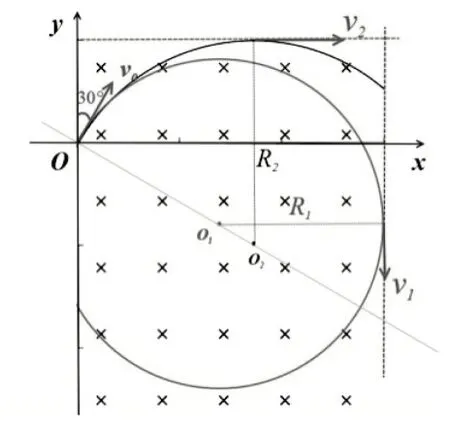
图7

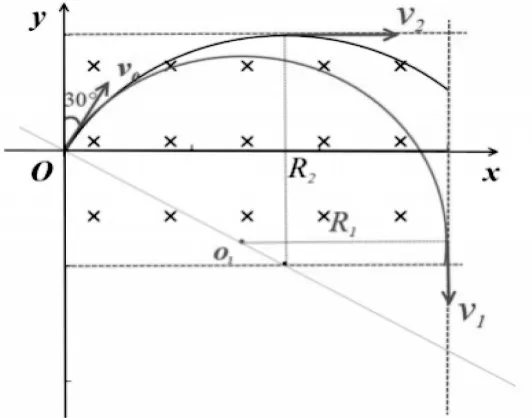
图8

边界越多，条件设置越多，问题愈加复杂，但知识的本质不变——放缩圆模型。粒子入射速度越小，运动轨迹对应的圆心角越大。当速度小到某个值时，轨迹将与下边界相切，进而发现从左边界射出磁场的粒子。其轨迹对应的圆心角最大，在磁场中运动的时间最长。

通过动画模拟，形象展示，帮助学生进一步完善放缩圆模型特点，对模型的认识更加清晰。速度大小各异的相同带电粒子（用不同颜色表示）同时、同方向垂直射入磁场（如图9所示），在磁场中运动相同时间，轨迹对应的圆心角相同；任意时刻，磁场中的各个粒子均分布在以入射点为轴心的同一转轴上。

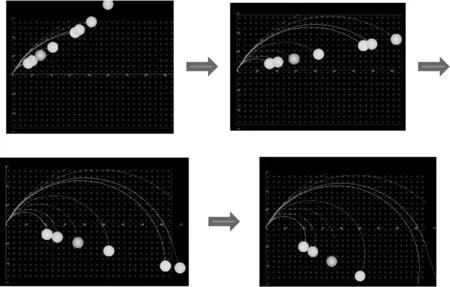
图9

四、变化问题情境，深化模型本质

丰富多样的问题情境，为学生搭建在具体情境中经历获取信息、选择信息、提取信息、解决新情境下的问题等认知过程的平台。常见的有界磁场有矩形、三角形、圆形、正六边形等等（如图10所示），学生在解决这些真实具体的问题过程，需要去除非本质属性的干扰——形状各异的边界，抓住模型本质——放缩圆模型，才能实现知识的有效迁移和应用。在迁移与应用中，学生将内化的知识外显化，将抽象的经验知识转化为具体的问题解决过程，即无论磁场边界是何形状，只要符合放缩圆模型条件的，即可将实际问题中的过程转换成对应的物理过程模型，通过分析推理，解决问题。

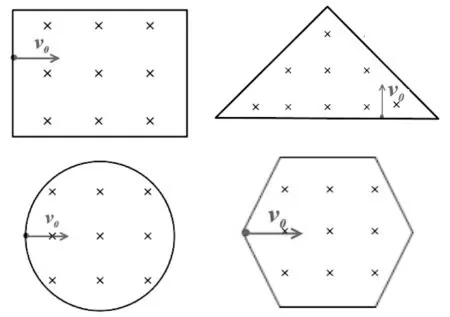
图10

五、灵活运用模型，解决真实问题

学习需要经历知识的获取、反思、感悟、理解、迁移和应用的过程，在应用中，再次经历建构新的认识、反思、感悟，形成新的思路和方法的螺旋式上升地体验。学习活动中，教师要设计富有挑战性的问题情境，让学生保持与真实问题情境的持续互动，促进学生与经验知识的深层次交流，深刻理解事物本质。在理解中尝试应用，在应用中深化理解。

［问题5］（2020年全国卷T18）一匀强磁场的磁感应强度大小为B，方向垂直于纸面向外，其边界如图11中虚线所示，ab为半圆，ac、bd与直径ab共线，ac间的距离等于半圆的半径。一束质量为m、电荷量为q（q＞0）的粒子，在纸面内从c点垂直于ac射入磁场，这些粒子具有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子，其运动时间为

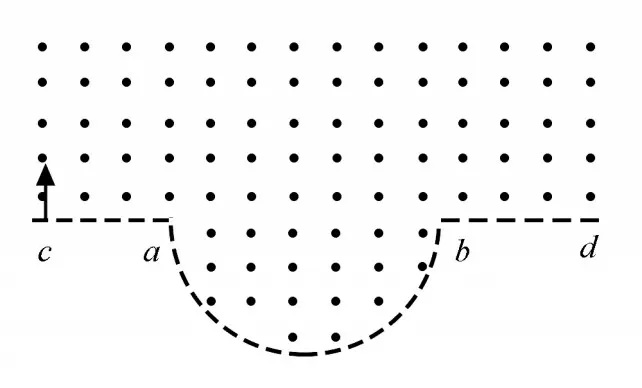
图11

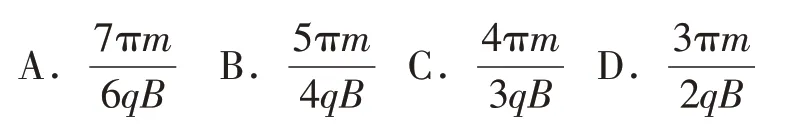
本题巧妙设置了直线边界与圆形边界相结合的有界磁场问题情境。学生要根据题意“从c点”“垂直于ac”“各种速率”等条件做出分析判断，这是属于带电粒子在磁场中运动的放缩圆模型：各种不同速率的带电粒子在匀强磁场中运动的周期相同，运动的时间取决于运动轨迹对应的圆心角。从直线边界ca或bd飞出磁场的带电粒子，圆心角为π；从半圆区飞出的粒子运动轨迹对应的圆心角更大；设粒子从半圆区的f点射出磁场，则cf与ca的夹角越大，所对应的圆心角也越大（如图12所示）；当cf与半圆相切时，粒子偏转的圆心角最大，在磁场中运动的时间最长。

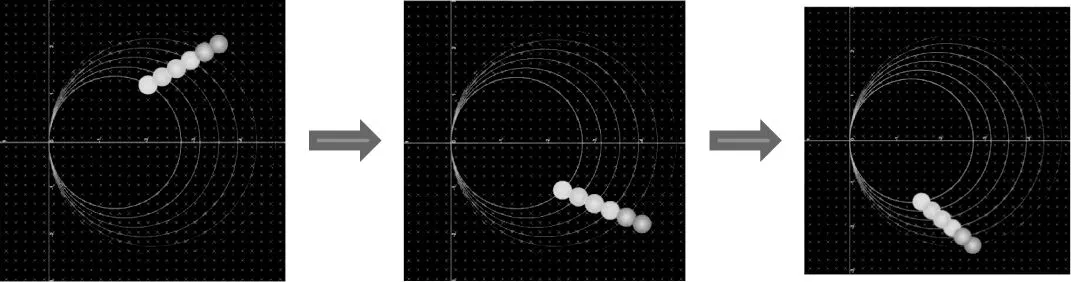
图12

正如国际经济合作与发展组织（OECD）在2005年遴选和界定核心素养时所明确指出的那样，核心素养是个体在面对复杂的、不确定的现实生活化情境时，表现出来的综合性品质。［3］只有让我们的学生有着丰富的解决真实问题的经历和体悟，把握事物的本质，才能认识本质的多样表现、各种变化。在经历和体悟中，扩展与提升经验，将内化的知识外显化、操作化，将抽象的符号转化为具体的问题解决过程，实现从提高解题能力向提高解决问题能力的转变，促进学生核心素养的养成和发展。