发挥数学的内在力量引导学生增强思考力

李平香 林运来

（1.三明市第二中学，福建三明 365000；2.厦门大学附属实验中学，福建漳州 363123）

“核心素养”是适应终身发展和社会发展需要的必备品格和关键能力.如何将“核心素养”转化为学生看得见用得上的素质能力？章建跃博士指出：根据核心素养与数学学科特征，应抓住整体性、系统思维和单元教学等关键词.实施单元教学能有效地把整体性教学和系统思维的培养融为一体［1］.数学学科核心素养之一是“数学思考”.“思考”是指“进行比较深刻、周到的思维活动”［2］；“思考”是思维的一种探索活动，“思考”的核心是“思考力”，“思考力”则是在思维过程中产生的一种具有积极性和创造性的作用力.2014年，吕传汉教授提出“教思考、教体验、教表达”的“三教”教育理念，吕教授指出，“教思考”旨在让学生学会“想数学”，促进学生思辨能力的培育［3］.在物理学中，力具有三个基本要素：大小、方向、作用点；在数学学习中，思考力同样离不开三个基本要素：大小、方向、作用点［4］.

在“整体—局部—整体”的单元教学方式中，前一个“整体”是先行组织者，是章节学习的“导游图”，主要呈现研究一个数学对象的概要思路、普适性的思想方法、解决问题的策略等，从宏观上解决“学什么”“怎么学”“为什么学”等问题，让学生能始终保持正确的路径和明确的方向；中间的“局部”是前一个“整体”中给出的研究方案的具体化，即对具体的每个知识进行研究；后一个“整体”是在分课时学习基础上的归纳、总结，不仅要完善本单元的知识结构，更要建立与相关知识的联系，从而使学生形成结构功能良好、迁移能力强的认知结构［1］.在日常教学实践中，教师往往对中间“局部”阶段的课时教学比较重视、擅长，对前后两个“整体”阶段的教学比较吃力，感到“实力不足”“底气不够”.本文以“圆锥曲线的方程”一章的教学为例，谈谈如何发挥“核心概念”“基本套路”“思想方法”等数学的内在力量，引导学生增强思考力的“大小”“方向”和“作用点”.

一、发挥“核心概念”的力量联通知识，在知识发展的内在逻辑中增强思考力的大小

思考力的大小取决于思考者掌握的关于思考对象的知识量和信息量的大小，如果没有相关的知识和信息，就不可能产生相关的思考活动.一般情况下，知识量和信息量越大，思考的维度就越加具体、全面和完整［4］.按“整体—局部—整体”的方式进行单元教学，中间的“局部”是前一个“整体”的细化，是“由薄到厚”的过程，即循序渐进地对数学对象的内涵与要素、概念的定义和表示、分类、性质、特例等展开研究，通过“如何归纳、抽象概念”“如何发现值得研究的问题”“如何研究性质”“如何找到证明的方法”等引导，使学生学习数学地认识和解决问题的具体方法［1］.后一个“整体”教学是在“局部”学习之后，更深入地揭示知识的联系与融合，是“由厚到薄”的过程.在后一个“整体”教学过程中，教师要立足系统思维，发挥核心概念（即大概念：是人们在探究物质及其变化本质的过程中所形成的高度抽象的思维产物，它具有统领具体概念和事实概念的作用［5］）的力量架设知识联结、融合的通道，将习得的知识形成网络，构建功能良好、迁移能力强的认知结构.利用核心概念的统领、纽带、桥梁、延展作用，在知识发展的内在逻辑中，自然地增强学生思考力的大小.

在“圆锥曲线的方程”单元教学中，利用“运算”“距离”“角度”“斜率”等核心概念得到了大量的结论，在这些“局部”的具体研究基础上，还需用系统论的方法对教材中具有内在逻辑关联性的内容进一步地提炼概括，建立联系方式，打通融合渠道，在形成整体认识，建构结构化、系统化的知识体系过程中，引导学生学会思考.［6］下面以联通椭圆定义教学设计为例：

（一）用“距离”联系，以“运算”区分

1.“距离之和”定义：课本对平面内到两个定点的距离之和、距离之差为常数的点的轨迹作了重点研究，详细探究了平面内两个定点F1，F2，一个动点M，若常数，则动点M的轨迹是什么曲线？若为常数，则动点的轨迹是什么曲线？还可以引导学生与“距离之商”“距离之积”为常数时，动点M的轨迹进行比较区别.

在推导椭圆标准方程的过程中，通过代数恒等变形，变换距离类型，实现距离转化，将椭圆的“距离之和”定义与“距离之比”定义建立联系，打通融合渠道.

（二）用“斜率”联系，以“运算”区分

1.“斜率之积”定义：课本第108页例3，如图1，设A，B两点的坐标分别为(-5，0)，(5，0)，直线AM，BM相交于点M，且它们的斜率之积是，求点M的轨迹方程.

第116页第11题，如图2，矩形ABCD中，|AB|=2a，|BC|=2b(a＞b＞0).E，F，G，H分别是矩形四条边的中点，R，S，T是线段OF的四等分点，R′，S′，T′是线段CF的四等分点.

证明直线ER与GR′、ES与GS′、ET与GT′的交点L，M，N都在椭圆上.

图1

图2

第146页第11题，已知△ABC的两个顶点A(-5，0)，B(5，0)，且AC，BC所在直线的斜率之积等于m(m≠0)，试探求顶点C的轨迹.同时，课本还与斜率之和、斜率之差、斜率之商的轨迹作比较（课本第146页习题第9题，第139页习题第11题，第109页练习第4题）.

在推导椭圆标准方程的过程中，通过代数恒等变形，把“距离”向“斜率”转化，实现椭圆的“距离定义”与“斜率定义”相联系，建立融合通道.

（三）用“圆”联系，以“伸缩、相切”区分

1.压缩圆：课本第108页例2，如图3，在圆x2+y2=4上任取一点P，过点P作x轴的垂线段PD，D为垂足.当点P在圆上运动时，线段PD的中点M的轨迹是什么？

2.拉伸圆:课本第115页习题第9题，如图4，DP⊥x轴，点M在DP的延长线上，且当点P在圆x2+y2=4上运动时，求点M的轨迹方程，并说明轨迹的形状.与例2相比，你有什么发现？

3.同心圆:如图5，平面上有两个同心圆，半径分别为a，b(a＞b＞0)，大圆上有动点A，半径OA与小圆交于B，AN⊥x于N，BM⊥AN于M，则M的轨迹是什么？并与用“压缩圆”的方式得到椭圆作比较.

4.圆+中垂线：课本第115页习题第6题，如图6，圆O的半径为定长r，A是圆O内一个定点，P是圆O上任意一点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在运动时，点Q的轨迹是什么？为什么？

5.过定点的动圆+定圆+内切：如图7，平面内过半径为2a的定圆F1内一定点F2且与定圆F1相切的动圆圆心M的轨迹是什么？

6.动圆+两内含定圆+内外切：课本第115页习题第10题，一动圆与圆x2+y2+6x+5=0外切，同时与圆x2+y2-6x-91=0内切，求动圆圆心的轨迹方程，并说明它是什么曲线.

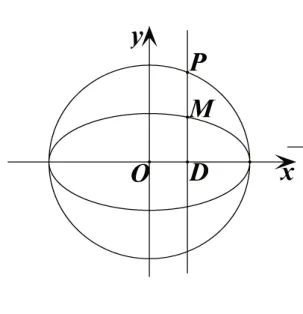
图3

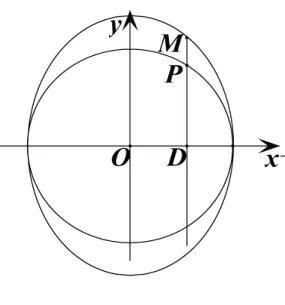
图4

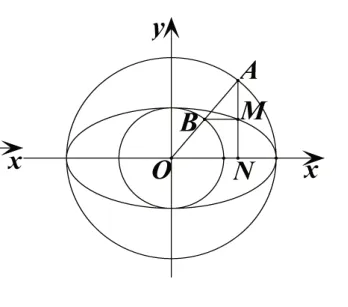
图5

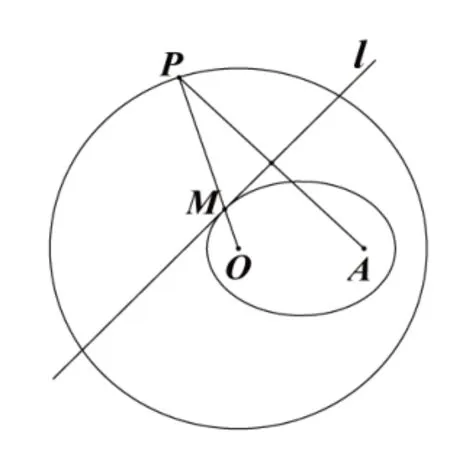
图6

图7

（四）用“圆锥”“圆柱”联系，以“截口”区分

1.截圆锥：再读课本章前语，如图8，用平面去截圆锥，截口曲线什么时候是椭圆、双曲线、抛物线？

2.截圆柱:如图9，用一个与圆柱母线斜交的平面截圆柱，截口曲线是椭圆.

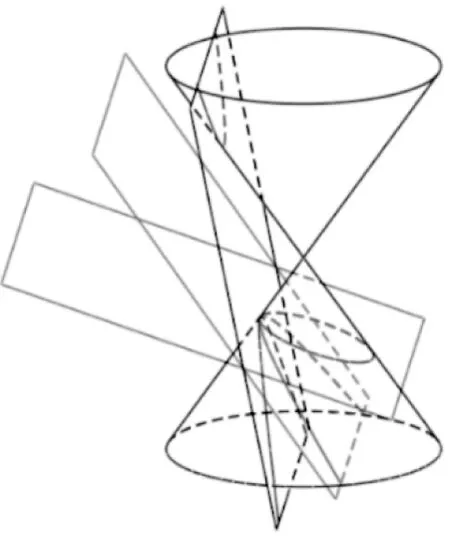
图8

3.拓展学习：比利时数学家Dandelin用双球把“截口曲线定义”，如图9、图10，与“距离定义”建立联系，统一了椭圆的定义.

上述教学立足系统思维，通过“距离”“斜率”等解析几何学科核心概念，以及“圆”“圆锥”“圆柱”等基本图形，结合“运算”“伸缩”“垂直”“相切”“截口”等具体方法，借助“核心概念”的强大力量将教材中出现的各种椭圆定义之间建立通道联系，并通过对比区别不同，在椭圆定义发展的道路上，引导学生从“见木”到“见林”的过程中，构建知识体系、积累可以迁移的研究经验，并能用类比的方法学习结构相似的其他圆锥曲线，进而在圆锥曲线定义发展的内在逻辑中，增强思考力的大小.

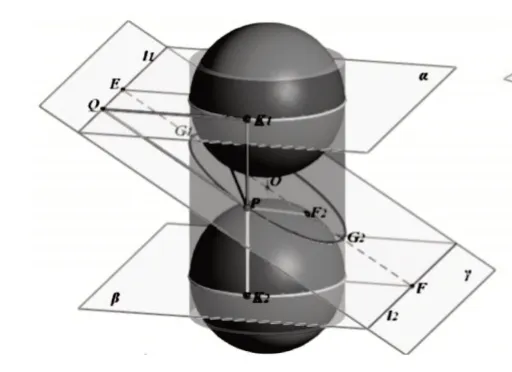
图9

图10

二、发挥“基本套路”的力量设计思路，在问题研究的逻辑思维中增强思考力的方向性

思考是一种有目的性、有计划性的思维活动，漫无目的地思考难以发挥强有力的思考力，常常会把思考引进死胡同，无果而终.因此，思考需要具有价值导向的思路引领，使思考更有目的性、方向性和一致性.所以，目的性、方向性、一致性和价值导向，决定着思考的角度和向度［4］.所谓的“套路”是指精心策划的应对某种情况的方式方法，使用该方式方法的人，往往已经对该方式方法熟练掌握，并且形成条件反射，逻辑上倾向于惯性使用这种应对方法以应对复杂的情况，心理上往往产生对此方法的依赖性［7］.以“问题引导学习”已成为数学教学的基本原则，教师如何通过“问题研究”让学生发展逻辑思维能力，学会思考呢？章建跃博士指出：依靠研究问题的“基本套路”.研究问题的“基本套路”的逻辑图，如图11，这就是“基本套路”.在教学中，如果一有机会就引导学生以这个逻辑图为指导展开思考活动，那么经过长期熏陶，就能使学生在潜移默化中养成一种思考习惯［8］.因此，教师要立足系统思维，善于发挥“基本套路”的力量，设计思考脉络，在问题研究的逻辑思维中，引导学生增强思考力的方向性.

在“圆锥曲线的方程”单元学习中，有许许多多的“二级结论”，如何发现这些结论呢？波利亚指出：“一个专心认真备课的教师能够拿出一个有意义但又不太复杂的题目，去帮助学生挖掘问题的各个侧面，通过这道试题就好比通过一道门户，把学生引入一个完整的理论领域”.发挥“基本套路”的力量，设计研究问题的思路，是引领学生进入“这个完整的理论领域”的有效途径.

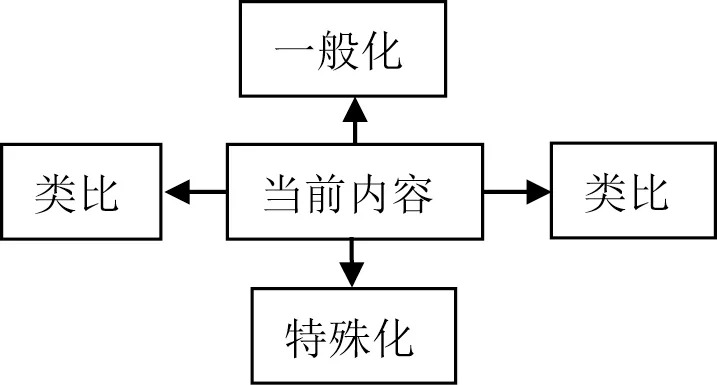
图11

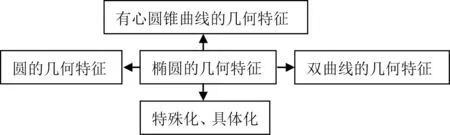
图12

在“联通椭圆定义”教学中，不论是从“距离”“斜率”等核心概念角度，还是从“圆”“圆锥”“圆柱”等基本图形角度研究椭圆定义，都充分发挥了“基本套路”的力量设计思路，使得研究方向明确.如在探究椭圆的几何特征时，首先，类比圆的几何特征，把“圆心”F这一个定点一分为二成“两个定点”F1，F2，设计探究问题：动点M到两定点F1，F2的距离之和是一个常数（大于|F1F2|）的点的轨迹是什么曲线？接着特殊化，设计探究问题：动点M到两定点F1，F2的距离之和等于|F1F2|这个常数的点的轨迹是什么曲线？然后，再类比“距离之和”的轨迹，自然生成“距离之差”的轨迹，设计问题：平面内与两个定点的距离之差等于常数的点的轨迹是什么？再进行平行类比，设计问题：比较平面内动点到两定点“距离之和”“距离之差”“距离之商”“距离之积”等于常数的点的轨迹.因为“距离”“斜率”都是解析几何的核心概念，把“距离”换成“斜率”，继续按上面设计问题的套路，设计探究“斜率之积”“斜率之商”“斜率之和”“斜率之差”的轨迹问题；最后，再一般化，设计探究这些圆锥曲线共同的几何特征.所以，在教学过程中，教师要注意发挥“基本套路”的力量，在圆锥曲线问题研究的逻辑思维发展过程中，如图12，增强思考力的方向性，找到更多的“好问题”.正如波利亚说：“好问题如同某种蘑菇，有些相似，它们大都成堆地生长.找到一个以后，你应当在周围再找找，很可能在附近就有几个.”所以用“问题引导学习”的关键是：引导学生“怎么找到好问题”.教学中要善于发挥“基本套路”的力量，通过类比、推广、一般化、特殊化、具体化、转化与化归等方法构建思考路径，从不同的视角、不同的层面进行改编、拓展、引申，在问题研究的逻辑思维中，引导学生增强思考力的方向性，在发现问题、提出问题、分析问题、解决问题的过程中，培养系统思维能力.

三、发挥“思想方法”的力量抓住本质，在着力点寻找的过程中增强思考力的聚焦性

思考力的作用点是指必须把思考集中在特定的对象上，并把握其中的关键点.如果找不准思考的着力点，就会精力分散、思维紊乱、胡思乱想，出现东一榔头西一棒槌的现象，使得思考停留在事物的表面上，浮光掠影，无法深入内核，更无法深刻认识事物的本质.思考在作用点上的集中性程度，决定着思考的强度和力度［4］.数学思想是对数学对象的本质认识，是认识具体数学概念、命题、规律、方法等过程中提炼概括的基本观点和根本想法，对数学活动具有普遍的指导意义，是数学活动的指导思想；数学方法是指数学活动中所采用的途径、方式、手段、策略等，是思想转化而来的具体操作方法，可以提高效果和效率.［9］在教学中，教师要善于发挥数学思想方法的力量抓住本质规律，在寻找着力点的过程中，引导学生增强思考力的聚焦性.

解析几何是用代数的方法研究几何问题，“坐标法”是解析几何的核心思想，也是解析几何的根本大法.教学中，既要善于借助坐标、方程、运算等思想方法的引领聚焦作用，还要兼顾几何图形的特征和性质，抓住问题的本质规律，在“坐标法”“几何特征”等关键点处着力思考.如在“联通椭圆定义”教学中，推导椭圆的标准方程时，得到移项，整理得此时，若将思考的着力点放在的几何意义上，设点A，B的坐标分别为(-1，0)，(a，0)，动点M(x，y)，则直线AM，BM的斜率之积是，特别地，当a=b时，kAM·kBM=-1，此时，动点M(x，y)的轨迹是以Ab为直径的圆，反之，直径所对的圆周角是直角，称为圆周角定理，类似地，若AB为椭圆直径（即过椭圆中心的弦），由点差法可证得称为椭圆周角定理.再将思考的着力点放在圆周角定理、垂径定理、平行弦中点性质、切线定理等圆的几何性质之间的逻辑关系上，把椭圆与圆类比，就可以得到椭圆非常多的“类圆性质”，即椭圆周角定理、垂径定理、平行弦中点性质、切线定理、以及它们之间的联系［6］，如图13.

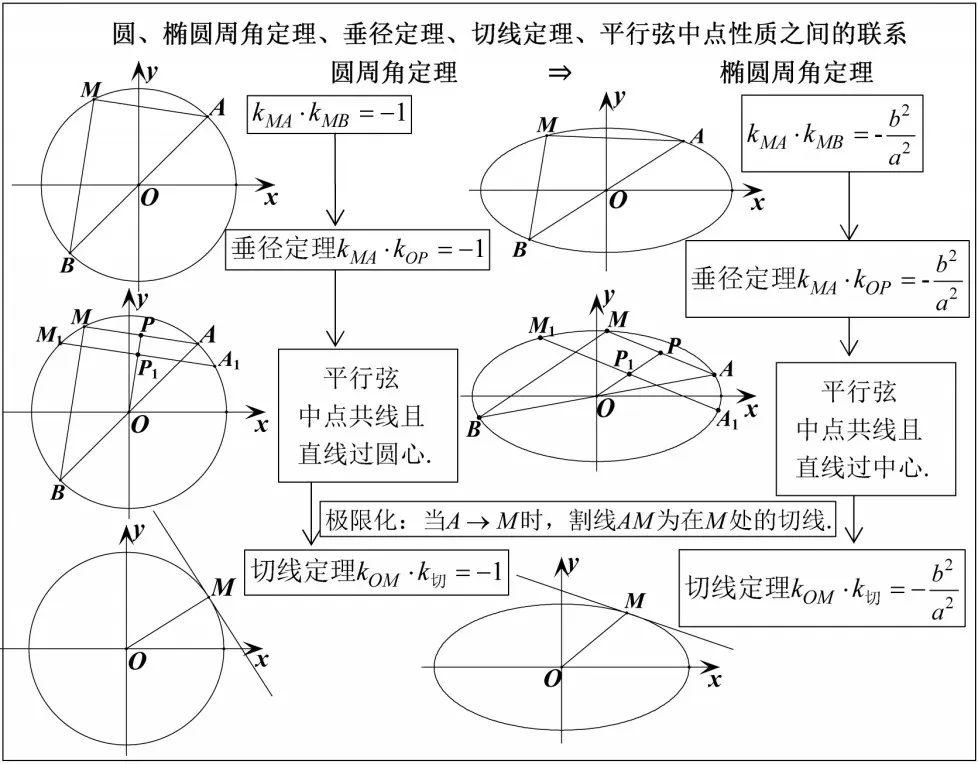
图13

（1）这组直线何时与椭圆相交？

（2）当它们与椭圆相交时，证明这些直线被椭圆截得的线段的中点在同一条直线上.

拓展应用：已知中心在原点的椭圆C的右焦点坐标为(1，0)，离心率等于

（1）求椭圆C的标准方程；

（2）证明：斜率为1的所有直线与椭圆C相交得到的弦的中点共线；

（3）图14中的曲线为某椭圆E的一部分，试作出椭圆E的中心，并写出作图步骤.

图14

在“联通椭圆定义”的教学基础上，把思考的着力点聚焦在圆周角定理，类比得到椭圆周角定理，继续把思考的着力点聚焦在圆的垂径定理、平行弦中点性质、切线定理等圆的几何性质之间的逻辑关系上，进一步类比可以得到椭圆的许多“类圆性质”，这些性质还可以继续类比、迁移、拓展到双曲线中，统一归纳为有心圆锥曲线的“类圆性质”.在“坐标法”思想指引下，着力在“坐标”“方程”“运算”“几何特征”等关键处思考，抓住了本质规律，所以，思如泉涌、威力无比、势不可挡.

四、结语

当前，学科核心素养的培养已成为教育热点.《普通高中数学课程标准（2017年版）》明确提出了数学学科的六大核心素养，而其本质就是数学思考.“思考”的核心是“思考力”.“核心概念”力量大，“基本套路”方向明，“思想方法”把脉准.教学中，应充发挥数学的内在力量，引导学生增强思考力的大小、方向、作用点，提升学生的数学素养，引导学生会用数学眼光观察世界，会用数学思维思考世界，会用数学语言表达世界［10］.