注重合情推理教学培养学生思维能力

陈建虹

（福州第二十四中学，福建福州 350015）

所谓合情推理，是指符合问题情景与情理的、自然的、似乎为真的推理，它是根据学生已有的数学事实、或数学经验和数学直观进行推测得到某些结论的一种推理.在思维方式上，常表现为凭直观感觉、或直觉和联想等非逻辑思维形式，通过学生对问题的观察、实验、猜想、归纳、类比等方法直接获得某种数学结论.初中阶段合情推理常用的思维方法是归纳推理和类比推理.

波利亚发现，可以机械地用来解决一切问题的“万能方法”是不存在的.在问题解决的过程中，人们总是针对具体问题与具体情况，不断地向自己提出有启发性与猜想性的问题，从而不断地启发与推进着思维的进展.［1］

初中数学教学历来讲究严密性、严谨性与逻辑性，十分重视对学生演绎推理能力方面的培养，而轻视了合情推理.实际上在数学的研究、科学的探索与日常的生活实践中，无不有着合情推理的影子，它有力地推动着数学学科的发展，是数学发现和创造的重要方法之一.因此在平时的课堂设计与数学的课堂教学中，教师应有意识、经常性地注重合情推理教学，鼓励学生对问题提出自己的看法与见解，培养学生养成良好的数学思维习惯，提高学生的整体思维能力.

一、创设问题情境，激发学生参与合情推理活动的兴趣

合情推理对初中生来讲并不陌生，在小学阶段已接触简单的合情推理训练.到了初中，尤其是开始几何的学习，对学生推理的要求高了，难度大了，但主要是对学生进行逻辑思维能力方面的培养，注重推理过程的严谨、严密与步步有据，注重套用“公式”“定理”或“口诀”等快捷的教学方式，解题时急于求成，没有进行必要的分析与推理，导致学生的思维僵化、刻板，对培养学生的思维能力尤其是创新思维能力十分不利.事实上，逻辑推理是论证的手段，合情推理是“发现”的工具，合情推理是发现真理的思维.学生具备了合情推理能力，在学习上学生会善于把实际的生活问题转化为数学问题，用数学的眼光观察、猜测、分析、归纳和总结数学的事实与结论，在课堂之外，在日常的生活实践中学生也会自觉应用这种能力.

所以，在数学教学活动中教师首先要改变教学观念，让合情推理走进课堂，走近学生.教师在课堂上要善于激发学生的推理兴趣，而创设恰当的问题情境是关键.合适的、耐人寻味的、恰到好处的问题，能够使学生学习兴趣盎然，思维活跃，对培养学生的自学能力与创新思维能力十分有利.［2］

其次，创设合情推理的问题情境，要紧密结合初中数学的教材内容.如在进行“有理数的乘方”的教学时，问题设计为:由一张厚度为0.1毫米的纸，

（1）将它对折1次后，厚度为多少毫米？对折2次厚度为多少毫米？对折3次、4次呢?

（2）对折30次后，厚度为多少毫米?

（3）如果我们教室的层高为4.5米，这张纸对折30次后有多少层教室的高度?

以上的教学过程，让学生经历了从折纸到猜想再到计算的过程，再引入乘方的概念.这样的教学设计，不仅有趣，而且给学生的印象十分深刻，提高了学生的学习兴趣，锻炼了学生的推理能力.

初中数学知识体系中无处不充满着合情推理的知识、内容与方法，初中数学的教学活动，处处皆可使用合情推理.如在进行分式的教学时，与学生共同复习完分数的性质与运算法则后，让学生大胆的推测与猜想分式的性质与运算法则；复习完一元一次方程的解法后，根据不等式的性质让学生先说说一元一次不等式的解法；学习如合并同类项时可以类比乘法分配律；推导平方差公式时，让学生自己归纳与发现等等.还有很多的内容教学时均可进行合情推理能力的训练.

二、设计层次性问题，激励学生参与合情推理活动的热情

问题是数学的心脏.明智的教师都会把枯燥的数学变为一个个有趣的问题呈现给学生，通过对问题的解决，达到培养学生数学推理能力的目的.但由于学生学力的差异，设计同层次的问题不利于班级的课堂教学，因而设计有层次的问题显得尤其重要.因此教师应根据教材内容，遵循层次性设计的原则，进行科学的、合乎情理的设计，才能在课堂上有意识地、有层次性的开展教学活动，从而让学生逐渐养成数学合情推理的思维习惯.再者，教师还要根据不同阶段的学生所具备的思维能力，设计适合的问题展开推理活动.太过简单的活动会让学生觉得索然无味，而太难的活动又会挫伤学生的学习信心.

如在“有理数的减法”教学时，教师根据“减法是加法的逆运算”得出3-（-3）=3+（+3）之后，让学生把3换成-2并写出等式，此时就可让学生进行大胆的推测与猜想有理数的减法可能怎么做，当然要让猜不出来的学生继续进行尝试，尝试的个数依学生的程度而决定，让“尝试—猜想—归纳”不断的交替进行.在这个过程中，不同层次的学生都参与了推理的活动，学生不断地进行着猜想、归纳、类比等各种思维方式的锻炼，同时能加速数学知识点的迁移，提升创新思维能力.

在学习“等腰三角形”这一节时，师生先一起回忆复习等腰三角形的概念后，让学生把一张长方形的纸按图中虚线对折，沿AB剪去阴影部分，再把它展开，得到一个△ABC，接着设计以下探究的问题，并要说出具体的推理理由.

（1）找出图中相等的线段和角，并说出理由；

（2）△ABC是轴对称图形吗？为什么？如果是，请说出对称轴.

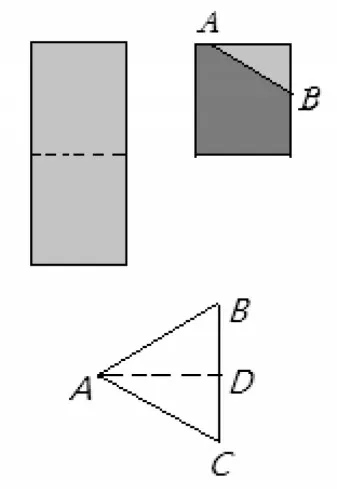
此时教师不要停止教学，而是引导学生回忆三角形中的三线，并结合以上的问题（2）中的对称轴，得出辅助线AD，进一步让学生进行观察、猜想、讨论，从而就顺其自然地得到了性质2，并要学生写出证明的过程.这充分体现了一个从观察、实验、猜想、论证的研究几何问题的全过程，也体现了从低到高的一个有层次性的合情推理过程.在这个过程中，教师并不是在高谈阔论，而是结合具体的操作步骤，引导学生大胆地进行推测与发现数学的事实，促进学生推理能力发展.

三、设计问题导向，引导学生开展合情推理活动的方向

合情推理是将一个命题在证明之前引导学生提出假设与猜想，这种由发现到猜想的过程就是合情推理.在引导学生对规律或结论进行探究时，根据问题的不同，适时给学生确定问题的导向或目标，然后对该目标进行观察和分析，据此提出一种可靠与合理的猜想.［3］

这就要求教师首先要认真分析教材，挖掘出其中有价值的、直观明了的数学问题，有的放矢地进行推理活动的设计.其次对数学问题要进行认真的分析与对比，让学生明确要解决的问题，引导学生开展有针对性的推理活动.如在学习“轴对称图形”时，教师可收集相关的生活中常见的图片，通过媒体让学生观察与比较，展开讨论与猜想，在此教师应舍得花时间，让学生自己发现与总结出结论.经过学生的探究与教师的指导得出轴对称的概念后，接着可设置以下问题：（1）成轴对称的两个图形全等吗？（2）如果把一个轴对称图形沿着对称轴分成两个图形，那么这两个图形全等吗？这两个图形对称吗？（3）请你说说成轴对称的两个图形有什么性质?在问题的引导下，学生的推理有了明确的方向，通过比较、类比与分析，自己得出了轴对称的相关性质.

当然，对学生偏离了方向的推理，教师不能简单地否定，而应抓住契机，引导学生分析，找出错误，进而提升学生的自我评判能力和反思能力.