长方体在培育直观想象素养中的实践与价值

张洁 林晴岚 陈柳娟

（福建教育学院数学教育研究所，福建福州 350025）

高中数学立体几何单元的学习内容安排重点是围绕发展学生的数学核心素养，遵循对事物的认识从具体到抽象、从整体到局部的原则，通过丰富的实物模型或利用计算机软件呈现空间几何体，有效地帮助学生认识空间几何体的结构特征，掌握在平面上表示空间图形的方法和技能，促进学生逐步形成空间观念.引导学生通过对图形的观察和操作，发现和提出描述基本图形平行、垂直关系的命题；学会用准确的数学符号语言表达相关命题，借助几何图形的直观解释命题的含义和表述证明的思路；［1］借助特定的、情境化的、综合性的数学活动提出针对性的数学问题，指导学生开展对立体几何问题的探究活动，促进学生学会从多角度、用联系的观点看待事物，更清晰地认识数学的科学价值、应用价值、人文价值和审美价值，提升学生的学习能力和综合素养.

学校的每一间教室建筑结构基本都以长方体为模型，把长方体作为学生认识与研究空间几何体的实景载体，有助于帮助学生直观地认识事物的位置关系，建立形与数的联系，掌握构建立体几何模型，开拓对空间几何相关问题的探究活动思路［2］，培育学生直观想象素养.

一、理解空间基本元素间的位置关系

长方体作为学生生活中最熟悉的立体几何图形，借助长方体来研究抽象的空间点、线、面间的位置关系，这是最自然、最容易接受的方式.如，研究空间直线与直线、直线与平面、平面与平面的位置关系.

［案例1］如图，借助长方体ABCD-A1B1C1D1研究空间线、面之间的位置关系

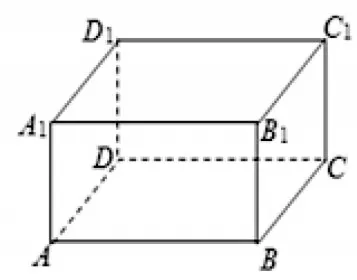
图1

如：1）直线AB与直线CD的位置关系；（直线AB与CD共面且平行即AB∥CD）

2）直线AB与直线B1C1的位置关系；（直线AB与B1C1异面且垂直即AB⊥B1C1）

3）直线AB与直线C1D1的位置关系；（直线AB与C1D1共面且平行即AB∥C1D1）

4）直线AB与平面AC的位置关系；（直线AB在平面AC内即AB⊂平面AC）

5）直线AB与平面B1D1的位置关系；（直线AB与平面B1D1平行即直线AB∥面B1D1）

6）直线AB与平面BC1的位置关系；（直线AB与平面BC1垂直即AB⊥面BC1）

7）平面AC与平面B1D1的位置关系；（平面AC与平面B1D1平行即面AC∥面B1D1）

8）平面AC与平面BC1的位置关系；（平面AC与平面BC1垂直即面AC⊥面B1D1）

从以上对长方体中的棱、面间的位置关系，直观理解抽象的空间线与线、线与面、面与面间的位置关系，学会用数学的图形语言、符号语言准确刻画出抽象的空间线、面之间位置关系：

1.直线与直线之间

共面关系：平行（a⊂α，b⊂α，a∥b）、相交（a⊂α，b⊂α，a∩b=P）；

异面关系：不在任何一个平面内（a⊂α，b⊄α，a∩b=∅）

2.直线与平面之间

线与面有公共点：线在面内（a⊂α）或线与面相交（a⊄α，a∩α=P）；

线与面无公共点：线与面平行（a∥α）

3.平面与平面之间

通过对空间位置关系的学习过程体会到：从已有的成熟基础模型出发建构新的知识体系，自然合理降低学生对新知识的理解难度；对抽象几何图形基于基础模型，合理将为问题转化，为问题解决提供了一个通性通法；借助基础模型的“固定形”为抽象图形的“变化形”提供一个“变”转“定”的基本解决问题路径，既为培养学生的空间想象能力搭建一个落地又扎实的脚手架，又为培育学生的直观想象素养奠定良好的基础.

二、理解空间线、面平行与垂直的有关定理

以长方体为空间几何体的基本研究载体，运用几何直观、空间想象，抽象出实物的几何图形位置关系（如线线平行、线面平行、线面垂直、面面垂直等）、运动规律、形态变化，认识和探索空间图形的性质，会用图形与集合符号语言精准表达空间点、线、面之间的位置关系.

［案例2］面面平行的判定定理如图2：若有一平面内的两条相交直线分别与另一平面平行，那么这两平面平行.即用数学的符号语言表述为：如图3，a⊂β，b⊂β，a∩b=P，a∥α，b∥α⇒β∥α.

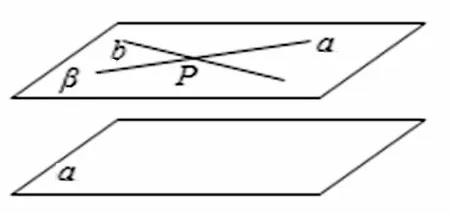
图2

借助长方体ABCD-A1B1C1D1的面、棱、面的对角线等，直观理解面面平行判定定理，如图3，直线A1D1⊂平面A1C1，直线A1B1⊂平面A1C1，直线A1D1∩直线A1B1=A1，直线A1D1∥平面AC，直线A1B1∥平面AC，即可直观得到：面AC∥面A1C1；理解直线A1D1⊂平面A1C，直线EF⊂平面A1C，直线A1D1∥平面AC，直线EF∥平面AC，也直观得到：平面A1C与平面A1C1相交，平面A1C与平面AC相交；更深入理解了面面平行的判定方法需借助两条相交直线而不是两条平行直线的合理性与严谨性.

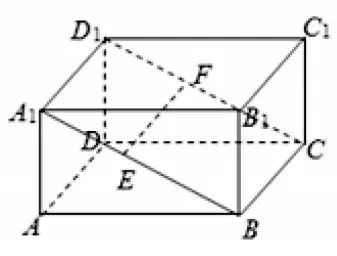
图3

［案例3］面面平行的性质定理：若两平面平行，有一个平面与两个平行平面都相交，那么这两条交线平行.即用数学的符号语言表述为：如图4，α∥β，γ∩α=a，γ∩β=b，⇒a∥b.

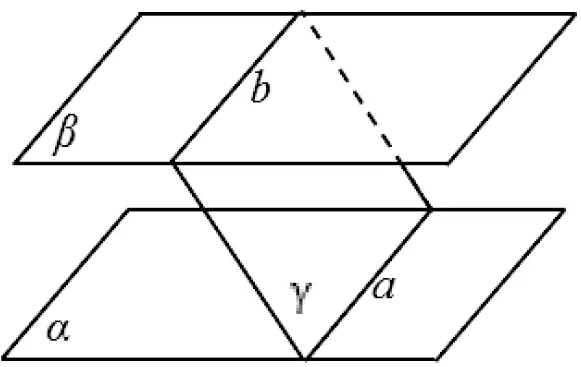
图4

借助长方体ABCD-A1B1C1D1直观理解面面平行性质定理，如图1，若两平行平面即可看成长方体中的面AC∥面A1C1，面A1D∩面A1C1=直线A1D1，面AC∩面A1D=直线AD，则直线A1D1∥直线AD，即长方体中棱A1D1所在直线A1D1与棱AD所在直线AD平行.

［案例4］直线与平面垂直的判定定理：如果一条直线与一个平面内的两条相交直线垂直，那么该直线垂直此平面.即用数学的符号语言表述为：如图5，c⊥a，c⊥b，a⊂β，b⊂β，a∩b=P⇒c⊥β.

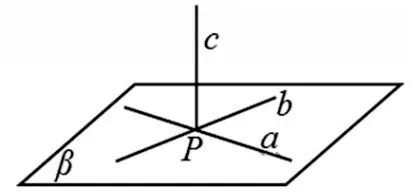
图5

借助长方体ABCD-A1B1C1D1直观理解直线与平面垂直判定定理，如图1，AA1⊥AB，AA1⊥AD，直线AB⊂面AC，直线AD⊂面AC，直线AB∩直线AD=A点，则直线AA1⊥平面AC.

由于空间线面平行与垂直关系有其严格的定义、判定、性质，掌握其定义、性质、判定是高中数学学习必修内容，厘清空间线面平行与垂直关系是后续进一步深入学习研究数学的基本要求.借助研究空间几何体的线面关系，特别是长方体中所呈现的线面关系，合理又严谨地把面间的平行与垂直的判定转换成线间的平行与垂直的判定，让学生体会合理“降维转化思想”，正确理解严谨地将空间问题与平面问题之间的转化基本要求，既能有效提高学生的空间想象能力和逻辑推理能力，又将培育学生的直观想象、逻辑推理素养落到实处.

三、理解空间图形的度量关系

高中数学研究空间图形的度量关系有：距离、角度、面积、体积等，度量关系的研究能有机融合“直观想象”与“数学运算”.通过研究空间的点到线、点到面、线与线间、线与面间、面与面间的距离，以及线线间、线面间、面面间的夹角，在此基础上进一步研究空间形与体的面积、体积等.借助长方体研究从现实世界中物体的形状、大小与位置中抽象出数学基本图形，直观理解空间图形的度量关系，帮助学生更好地掌握图形研究的基本思想方法.

［案例5］如图6，在长方体ABCD-A1B1C1D1中，AB=2，BC=CC1=1，

1）求直线CC1与平面BDD1B1的距离；2）求四棱锥ABDD1B1的体积.

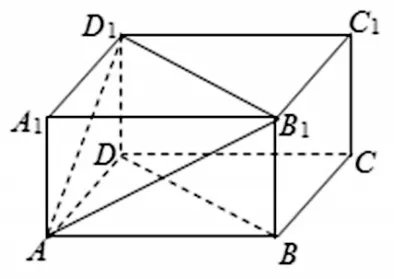
图6

问题分析：1）求直线CC1与平面BDD1B1的距离需借助长方体的结构特征，将所求距离转化为寻找同时与直线CC1、平面BDD1B1垂直的垂线段CH（如图7），进而求垂线段CH的长度达到解决问题的目的；2）求四棱锥A-BDD1B1的体积也同样需借助对长方体的结构特征研究，得到可从长方体ABCD-A1B1C1D1中切除相关柱体 BCD-B1C1D1与锥体 AA1D1B1，将所求问题转化，达到求四棱锥A-BDD1B1的体积的目标.

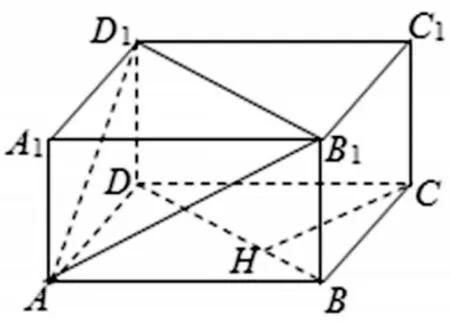
图7

此类问题的研究有助于评价学生对长方体的结构特征掌握程度，以及评价学生对线面间距离的求法、简单几何体的体积求法中运用数学基本思想方法解决问题的能力，有机融合“直观想象”与“数学运算”素养的培育.

四、解决实际问题中的应用价值

以长方体为基本模型，通过对“几何图形”的直观想象与“数学运算”的有机融合，自然将“形”和“数”联.以基本几何图形为基础，学会从“基本图形”研究，到“变形图形”研究，再到“综合图形”的研究.

［案例6］如图8，在长方体ABCD-A1B1C1D1中，AB=3，BC=4，且在棱CC1上存在点M，使MD1+MA取得最小值10，此时长方体的对角线DB1与平面ADD1A1、ABCD、DCC1D1所成的角分别为α、β、θ，则sinα+sinβ+sinθ=.

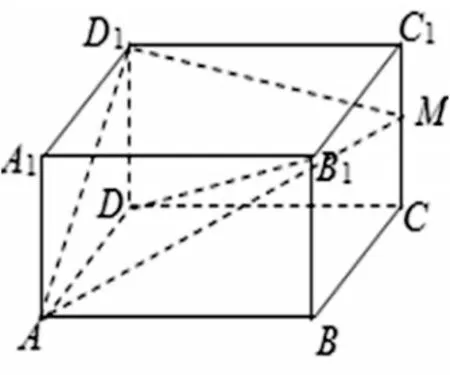
图8

问题分析：要使MD1+MA取得最小值10，需将MD1+MA放在同一平面进行思考，即将平面ACC1A1与平面DCC1D1沿C1C翻折打开，使得平面A1ACC1与平面D1DCC1在同一平面内，如图9，当A，M，D1在同一条直线上时，MD1+MA取得最小值，即为AD1的长，易 知 AC=5，CD=3，DD1=-82=6，在长方体中，由长方体的性质可知，∠A1DB1=α，∠BDB1=β，∠C1DB1=θ，

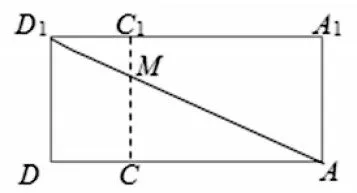
图9

长方体是一个空间基础的、稳定的、可靠的、有效的模型，借助长方体模型将复杂空间图形的问题通过合理、严谨的方式转化成平面图形的问题进行研究，这是一个行之有效的常规方法.处理平面问题是将学生已熟悉的、有把握能解决的，转化为平面问题，这对学生会产生心理上的踏实感.转化过程让学生进一步厘清了直观与想象的关系，体会实物的位置关系、对称特性、运动规律和形态变化［2］，更好地把握利用图形描述、分析数学问题，通过合理方式探索解决问题的思路［2］，掌握对空间几何体进行加工、改造，创造新的几何体进行研究的技术手段，培育学生的直观想象素养.

借助长方体能将复杂图形和背景转换到具体的直观的模型上，是一个转换思想的具体体现，在立体几何学习中，是一个基础的、有效的、有力的解决空间问题的转换思路之一.在转换的过程中，对空间几何图形的直观想象将以更直观的形式逐层展开，从体的直观合理转化到平面的直观，再从线的直观回到面的直观和体的直观，循环往复，加深理解，提高素养.在高中数学选择性必修课程内容中，学生将学习空间直角坐标系，进一步深入理解空间几何基本要素，掌握形与数间的一一对应关系，拓展探索空间问题解决的思路，领会到直观想象在数学解决问题活动中是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础［2］.