二维高陈数模型中Bloch电子的拓扑刻画

刘佳斌，于肇贤，王宏伟，马余全

(北京信息科技大学 理学院，北京 100192)

0 引言

对新奇物态和相变的研究一直是凝聚态物理的理论前沿。朗道相变理论可以通过自发对称性破缺原理对相进行分类。但是随着对量子Hall效应的深入研究，发现朗道相变理论无法对其相变进行解释。这是因为引起量子Hall效应的量子态并不存在对称性破缺，相变的产生源于一种拓扑相。随着分数量子Hall效应[1]、反常量子Hall效应[2]、拓扑绝缘体[3-4]以及拓扑超导[5]等大量无法使用朗道相变理论解释的现象出现，物理学界开始引入量子信息和量子态空间几何中的概念来研究量子相变。

从量子信息中引入了量子保真度和保真率的概念。Zanardi等[6]在一维横场XY模型和Dicke模型中利用体系基态的量子保真度确定了系统的临界点。周焕强等[7]研究了量子保真度与临界标度和重整化之间的关系。陈澍等[8]对具有次近邻相互作用的海森堡链的基态和激发态保真度进行了研究。尤文龙等[9]确立了量子基态保真率与系统虚时关联函数的内在联系，并成功地标识了系统的量子相变和拓扑相变的相边界。在量子态空间几何角度，认识到Berry相位其本质为系统波函数在哈密顿参数空间中绝热演化所诱导的厄米线丛上的和乐(holonomy)后，物理学界发现量子多体系统的基态Berry相位与系统的量子相变关系极大。Parchos等[10]在一维横场各向异性XY自旋模型中发现了基态Berry相位和其与第一激发态的Berry相位差在相变点均出现有限的跳跃。朱诗亮[11]证明了一维横场XY模型的基态Berry相位对参数的微商在相变点奇异。

量子保真度、量子保真率以及Berry相都是参数空间中的局域量，不能全面反映量子态的拓扑性质，所以引入了量子几何张量。量子保真度和Berry相位两种途径可以在量子几何张量的概念下得到统一的理解。它的实部是由Provost和Valee[12]提出的一种(半正定的)度规张量，它定义了系统Hilbert参数空间中两个毗邻量子态之间具有U(1)规范不变性的距离，对应于量子保真度。M.V.Berry[13]指出量子几何张量的虚部正比于Berry曲率。

Haldane[14]将量子几何张量引入分数量子Hall态的研究，发现了量子几何张量和Hall粘滞度的重要联系。2013年，马余全等[15]提出了利用能带拓扑欧拉数来表示某些具有能隙的费米系统的非平庸拓扑相，拓扑欧拉数利用能带在第一布里渊区上的黎曼度规张量，根据高斯—博内定理而求出。实验中在可调控的超导量子电路上可以直接测出量子度规张量，并且能在一个时间反演不变的两能级系统中观测到由能带拓扑欧拉数所标志的拓扑量子相变[16-17]，从而直接验证了能带拓扑欧拉数的正确性。使用量子几何张量分析多体量子系统的新奇物态和相变现象既拥有实验结果的支持，又能够全面而深刻地揭示量子多体系统的拓扑性质，所以已经成为当前凝聚态物理的研究热点。

本文将使用量子几何张量对二维空间中两能带高陈数格点模型进行研究。这个模型由D.Sticlet[18]等首先提出，模型在费米子原子组成的三角晶格上实现，每个格点都有一个内部轨道自由度。类似于Hofstadter模型[19]，模型中电子的跃迁概率幅是复数，这种复跃迁的电子行为会破坏系统的时间反演对称性。根据模型Bloch动量空间中的哈密顿量，能够计算出系统的量子几何张量，并得到相应的Berry曲率和度规张量。能带的第一类陈数由Berry曲率在第一布里渊区上的积分得到。将度规张量限定在正定区域，那么度规张量也是一种黎曼度规，运用高斯—博内定理，在第一布里渊区的闭合Bloch态流形上计算出能带的拓扑欧拉数，这种拓扑序[20]与第一类陈数不同，同时给出了模型的第一类陈数和拓扑欧拉数的相图。第一类陈数和拓扑欧拉数是基于量子几何张量的一种直观简单的研究方法，它超越了朗道相变理论框架，全面地刻画了高陈数模型的拓扑量子相变现象，并进一步揭示了低维量子体系的拓扑性质，为探索新奇量子态和相变提供了理论方法支持。

1 陈数和拓扑欧拉数

计算能带的第一类陈数和拓扑欧拉数，首先引入Bloch动量空间中的量子几何张量。它由系统Bloch态U(1)线丛上的两个毗邻态之间规范不变的度量导出，这里的U(1)线丛是由第n个能级的Bloch态|un(k)〉的绝热演化得到。两个相邻Bloch态|un(k)〉和|un(k+δk)〉之间的量子度规为

(1)

其中μ和ν表示kμ和kν。|∂μun(k)〉将分解为

|∂μun(k)〉=|Dμun(k)〉+[1-P(k)]|∂μun(k)〉

(2)

式中Pn(k)=|un(k)〉〈un(k)|为投影算符，在线丛上|un(k)〉的协变导数为|Dμun(k)〉=Pn(k)|∂μun(k)〉。量子绝热近似保证了|un(k)〉到|un(k+δk)〉在U(1)线丛上的平行输运，故|Dμun(k)〉=0。因此，将式(2)代入式(1)得到量子度规：

dS2=

(3)

由此给出量子几何张量为

(4)

现在求能带的第一类陈数和拓扑欧拉数。在二维动量空间中，第一布里渊区的拓扑结构是一个二维的环面，考虑二维动量空间中的哈密顿量，Bloch态|un(k)〉会随着系统哈密顿量参数的量子绝热演化诱导出一个U(1)线丛。U(1)线丛上所有填充带的拓扑不变量是第一类陈数，量子几何张量的虚部(Berry曲率)在布里渊区上积分得到第一类陈数：

(5)

由量子几何张量实部计算出的拓扑欧拉数同样具有拓扑不变性，根据高斯—博内定理，拓扑欧拉数为

(6)

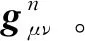
(7)

式中Rn为与Bloch态|un(k)〉相联系的里奇曲率。

在二维准动量空间k=(kx,ky)中，两能带Bloch态的哈密顿量为

(8)

式中：ε(kx,ky)为哈密顿量的特征值；I2×2为2×2单位矩阵；σα为泡利矩阵，表示赝自旋自由度；dα为泡利矩阵的系数。哈密顿量的本征能级为

(9)

哈密顿量的本征向量为

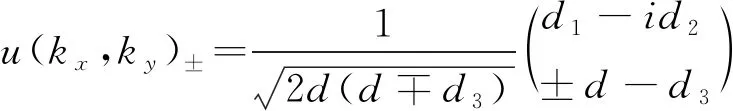
(10)

已知Pn(k)=|un(k)〉〈un(k)|，选用低能带Bloch态|un(k)_〉，将其代入式(4)得到量子几何张量：

Qkxky=〈∂kxu-|[1-|u-〉〈u-|]|∂kyu-〉

(11)

Fkxky=-2ImQkxky=

〈∂kxu-|∂kyu-〉-〈∂kyu-|∂kxu-〉

(12)

将式(10)代入式(12)得到Berry曲率：

(13)

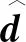
(14)

量子度规的计算是复杂的，量子度规行列式detgkxky却与布洛赫态|un(k)〉存在一种简单的关系：

(15)

通过式(13)和式(15)的比较得到量子度规行列式detgkxky与Berry曲率之间的关系detgkxky=(Fkxky)2/4。将式(15)代入式(7)得到能带拓扑欧拉数：

(16)

将式(13)代入式(5)得到第一类陈数：

(17)

2 高陈数模型

本文选择了一个具有高陈数的格点模型[21]作为例子，该模型具有丰富的拓扑物态。已知该模型Bloch动量空间中的哈密顿量为

H(k)=2t1cos(kx)σ1+2t1cos(ky)σ2+

{2t2cos(kx+ky)+2t3[sin(kx)+sin(ky)]}σ3

(18)

根据式(8)，从式(18)中得到系数：

ε(kx,ky)=0，d1=2t1cos(kx)，d2=2t1cos(ky)以及d3=2t2cos(kx+ky)+2t3[sin(kx)+sin(ky)]。将上述系数代入式(13)得到Berry曲率：

Fkxky=

(19)

将式(19)代入detgkxky=(Fkxky)2/4得到量子度规行列式：

detgkxky=

(20)

从式(19)和式(20)中知道Fkxky和detgkxky都是t2的函数。

已知两能带模型中的里奇曲率R恒定为8，将式(15)代入式(16)得到能带拓扑欧拉数：

(21)

将式(20)代入式(21)得到能带拓扑欧拉数的数值结果，如图1所示。

图1 能带拓扑欧拉数随参数t2的变化

可以观察到能带拓扑欧拉数并不总是一个精确的偶数，在3个奇异点t2=-1、t2=0和t2=1处呈现出冠状曲线。将式(19)代入式(5)得到能带的第一类陈数：

(22)

可以使用第一类陈数来划分相图，如图2所示。

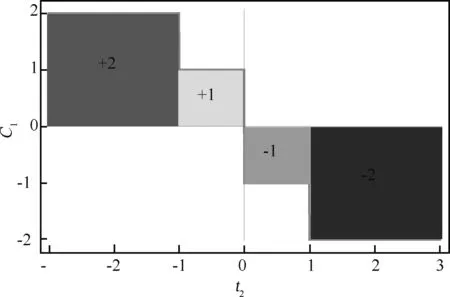
图2 能带的第一类陈数随参数t2的变化

在二维准动量空间中，将能带拓扑欧拉数和第一类陈数进行比较。当t2<1时，拓扑欧拉数出现稳定值，其数值为对应第一类陈数值绝对值的2倍。在-1

3 结束语

本文研究了两能带高陈数格点模型中Bloch电子的量子几何张量。基于量子几何张量的实部给出Bloch态流形的量子度规，利用高斯—博内定理在第一布里渊区Bloch态流形上，得到了能带拓扑欧拉数；在第一布里渊区对量子几何张量的虚部进行积分得到能带的第一类陈数，两者都可以作为拓扑序来划分相图。发现高陈数拓扑绝缘体拥有极其丰富的拓扑量子相变现象。当前使用拓扑欧拉数和第一类陈数等具有几何和拓扑的概念来揭示量子多体系统的拓扑量子相变，已经成为研究的热点。在二维严格可解量子系统及具有相互作用的自旋与费米系统中，研究它们的量子几何张量、第一类陈数以及拓扑欧拉数与拓扑量子相变的联系，对于深入理解量子系统的宏观量子特性和调控性，以及探索新奇量子态和奇异物性提供了必要的理论支持。本文的研究方法可应用在大多数二维严格可解的自旋以及费米模型中，如Haldane模型[22]、Kitaev模型[23]、Kane-Mele模型[3-4]。研究其能带拓扑欧拉数与其他拓扑量子数的联系可以进一步揭示低维量子体系的一些新的几何和拓扑性质。