反应堆压紧弹簧的仿真与参数灵敏度分析
2021-05-20郭昭良高凯烨
郭昭良,米 洁,薛 冰,高凯烨
(1.北京信息科技大学 机电工程学院,北京 100192;2.北京信息科技大学 经济管理学院,北京 100192)
0 引言
堆内构件压紧弹簧是一种轴对称结构的弹性环,是反应堆内部重要的支撑部件。在工作状态下,压紧弹簧为上部支承法兰起到一定的支撑作用,并且为吊篮筒体法兰提供足够的压紧力。在反应堆正常运行过程中,压紧弹簧承受热应力、压紧力等载荷,工作状态较为恶劣,其强度直接影响到反应堆的可靠性与安全性。张智峰等[1]总结了核电压紧弹簧制造技术及我国的制造经验,并评估了国内几种弹簧锻件的力学性能。李宁等[2]研究了压紧弹簧的锻环制造技术,分析了材料及技术参数对锻环强度和力学性能的影响规律,优化了锻环的制造工艺。
目前我国对压水堆核电站结构评定主要参照ASME规范和RCC—M规范[3],根据材料强度设计规范计算结构的许用应力,并通过与结构的实际应力进行比较,从而评定结构的强度。在实际条件下,由于材料化学成分、加工条件的差别以及工况条件的波动,压紧弹簧的材料属性、结构尺寸、所受载荷具有随机性,会造成压紧弹簧所受应力的随机性,从而对强度评定造成影响。考虑参数随机性的影响,对机械结构进行应力、强度分析,所得结论更符合实际。ZHANG等[4]基于班卓法兰的可靠性设计理论公式,利用扰动等方法,实现了随机参数影响下的法兰稳健可靠度设计。金永平等[5]建立了深海钻机关键部件的可靠性模型,运用随机数值分析的方法,得到了分析对象的可靠度,并通过样机实验验证了分析结果。Benammar 等[6]对定日镜的主要部件进行了数学建模,考虑了外载荷、几何特性等的不确定性,进行了可靠性分析。
由于不同的属性参数对压紧弹簧的可靠性具有不同的影响,研究各因素的可靠性、灵敏度并找出影响程度较大的因素,对工程实际具有较大的参考价值。通过灵敏度分析,可以得到可靠性变化和不确定变量分布参数变化的关系,进而为可靠性分析和可靠性优化设计提供理论指导[7]。
1 压紧弹簧模型建立
为考虑尺寸参数随机性的影响,对压紧弹簧进行参数化建模,将压紧弹簧内径、外径、上凸起高、下凸起高、弹簧中部高度定义为参数,关键参数的建模尺寸取值如表1所示。

表1 压紧弹簧参数表
根据压紧弹簧轴对称的特性,对其截面进行几何建模,并旋转拉伸,截面示意图如图1所示。其截面不是标准的矩形,在上下压紧部位有近似半圆状。
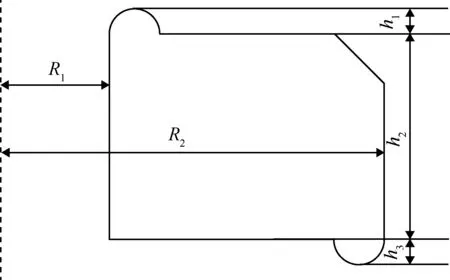
图1 模型几何结构示意
2 压紧弹簧的热应力仿真分析
根据压紧弹簧工作的实际工况条件进行热应力仿真。压紧弹簧材料为SA-182 F6a马氏体不锈钢,其材料参数如表2所示。

表2 材料参数表
使用ANSYS workbench软件对其进行热应力仿真,具体仿真流程如下。
1) 网格划分。为保证仿真结果的准确性,对模型的整体进行加密,设置网格大小为14 mm。网格平均偏度为0.484 25,平均雅阁比数为1.223 5,网格质量较好。整体网格划分结果和局部放大图如图2所示。

图2 整体网格划分与局部放大
2) 边界条件处理。压紧弹簧的工作位置如图3所示。弹簧上部压紧部位承受上部组件的重力作用,添加压紧力载荷于压紧弹簧上表面与上部支承法兰接触处,大小为3 153 000 N。根据软件测定模型体积为0.107 63 m3,取重力加速度为9.8 m/s2,计算得到压紧弹簧所受重力为8 174.50 N,对模型整体添加该重力载荷。
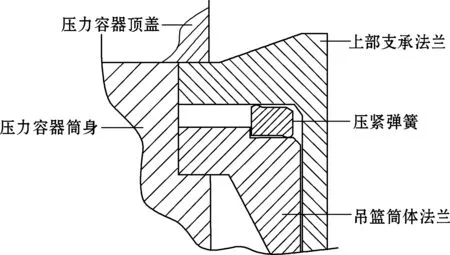
图3 压紧弹簧工作位置示意
压紧弹簧与吊篮筒体法兰压紧接触,将之简化为接触处的固定约束,即全自由度约束。
压紧弹簧还受到温度载荷的影响,对模型整体添加350 ℃的温度载荷。边界条件处理示意如图4所示。
3) 仿真结果分析。应力、应变、位移仿真结果如图5所示,应力、应变、位移最大值如表3所示。仿真结果显示,应力、应变最大值主要集中于压紧弹簧与上部支承法兰的接触面处,而位移最大值出现在压紧弹簧上表面外圈处。

图4 仿真边界设置示意

图5 应力、应变、位移结果云图

表3 仿真分析结果
3 压紧弹簧的灵敏度分析
3.1 输入参数分布特征
基于热应力确定性分析仿真的结果,使用ANSYS Workbench的六西格玛模块对压紧弹簧进行不确定性分析。
根据压紧弹簧的参数化模型,选择内径、外径、上凸起高、下凸起高、弹簧中部高度为随机参数。其中压紧弹簧的内径不能大于上凸起顶点位置,外径不能小于下凸起顶点位置,设置内径、外径服从截尾正态分布,上凸起高、下凸起高、弹簧中部高度为正态分布。
选择模型材料的杨氏模量、泊松比作为不确定性分析材料属性参数方面的随机输入,设定其在标准值上下1%以内波动,选择截尾正态分布表征[8]。
载荷参数方面设定压紧弹簧上表面的压紧载荷。查阅相关手册得知,压紧弹簧的压缩量在一定范围内波动,根据式(1)[9]可以计算得出压紧力的变化范围为2.997 5×106~3.308 5×106N。
(1)
式中:a为压紧弹簧被绕压曲段的宽度;Φ为弹簧的尺寸系数;E为弹性模量;Jx为绕截面中性面的惯性矩;δ为弹簧的压缩量。
指定最大应力、应变、位移的最大值为输出。不确定性分析变量分布特征如表4所示。

表4 不确定性分析输入变量分布特征
3.2 参数抽样及拟合验证
不确定性分析的输入变量为6个,热应力仿真使用的其他参数,如重力加速度、结构尺寸参数等设置为定值。对于每个输入变量,在对应分布区间内,选择拉丁超立方抽样(Latin Hyercube)方法,该方法具有抽样“记忆”功能,可以避免直接抽样法数据点集中而导致的仿真循环重复问题[11]。依据变量的分布特征对输入变量进行抽样和组合,得到46组数据集,将每组数据输入仿真模块,计算每一组输入数据得出的热应力、应变,统计并拟合得出输入变量和输出的函数关系,生成响应面模型。
由于响应面模型是软件自动计算生成,为验证模型的准确性,可通过软件的搜索算法计算响应面模型输出变量的属性。此处取变量的可决系数,可决系数越接近1,证明模型越准确。通过计算变量的拟合结果及交叉验证得到输出变量的可决系数,结果如表5所示。
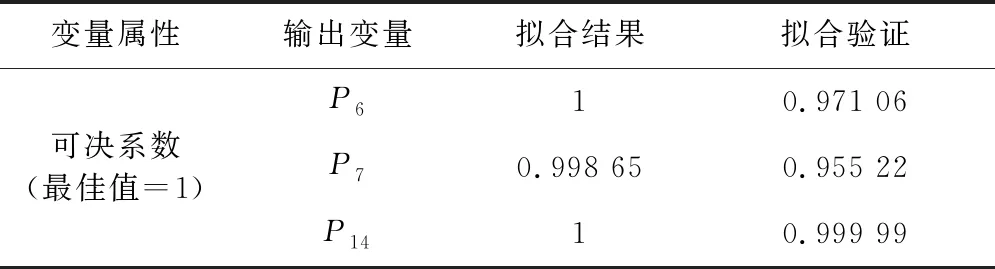
表5 模型输出变量准确性验证
结果显示,所有输出参数的可决系数均接近最佳值,回归验证结果如图6所示,其中横坐标为设计点观测值,纵坐标为响应面预测值。由图可知,应力、应变、位移的观测坐标位置贴合预测直线,拟合程度较高,模型准确。
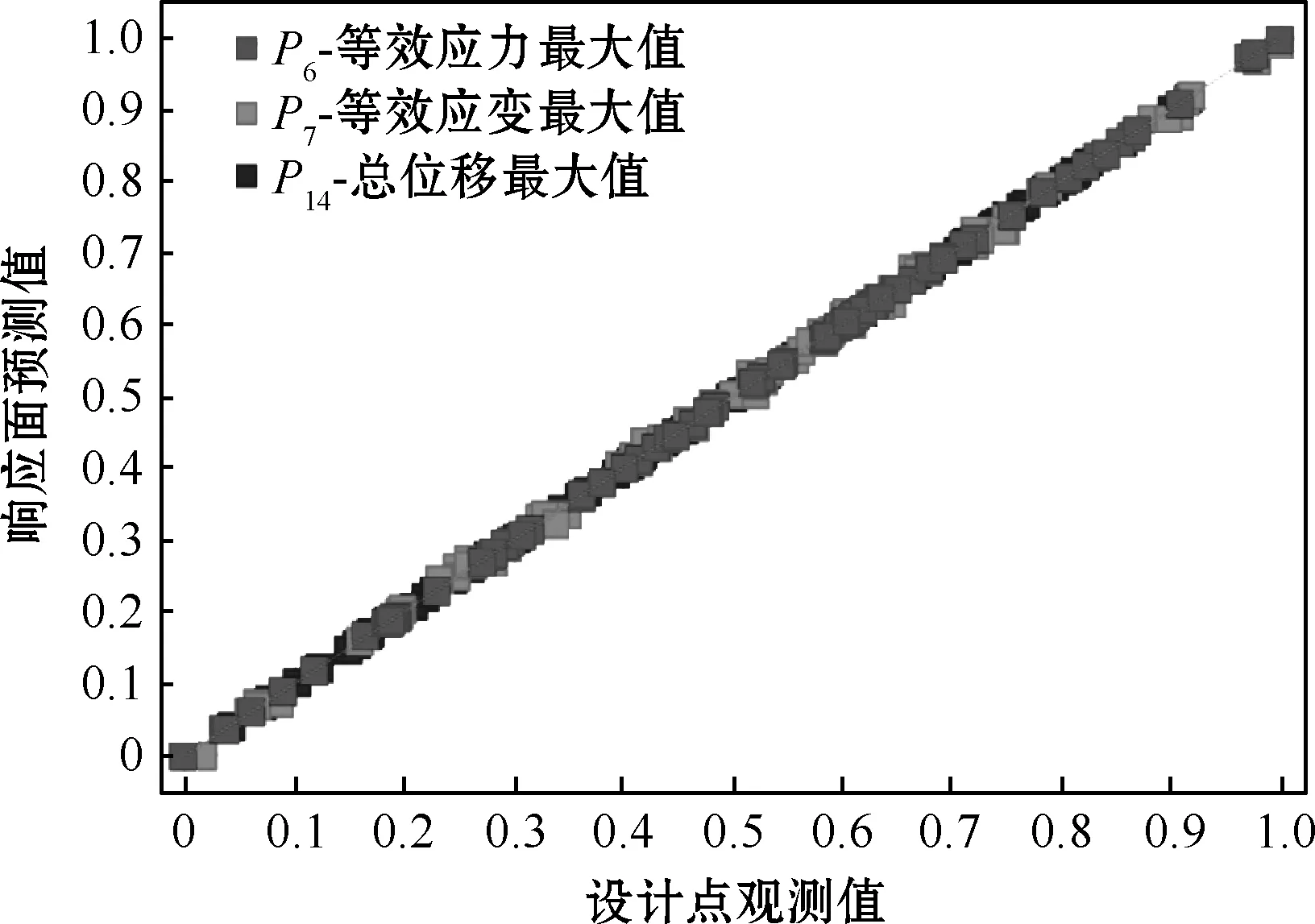
图6 响应面模型回归验证
3.3 分析结果输出及处理
对响应面模型进行10 000组蒙特卡洛模拟仿真,将P6、P7、P14的计算结果进行统计,并拟合得到分布曲线如图7~9所示。拟合结果均服从正态分布。
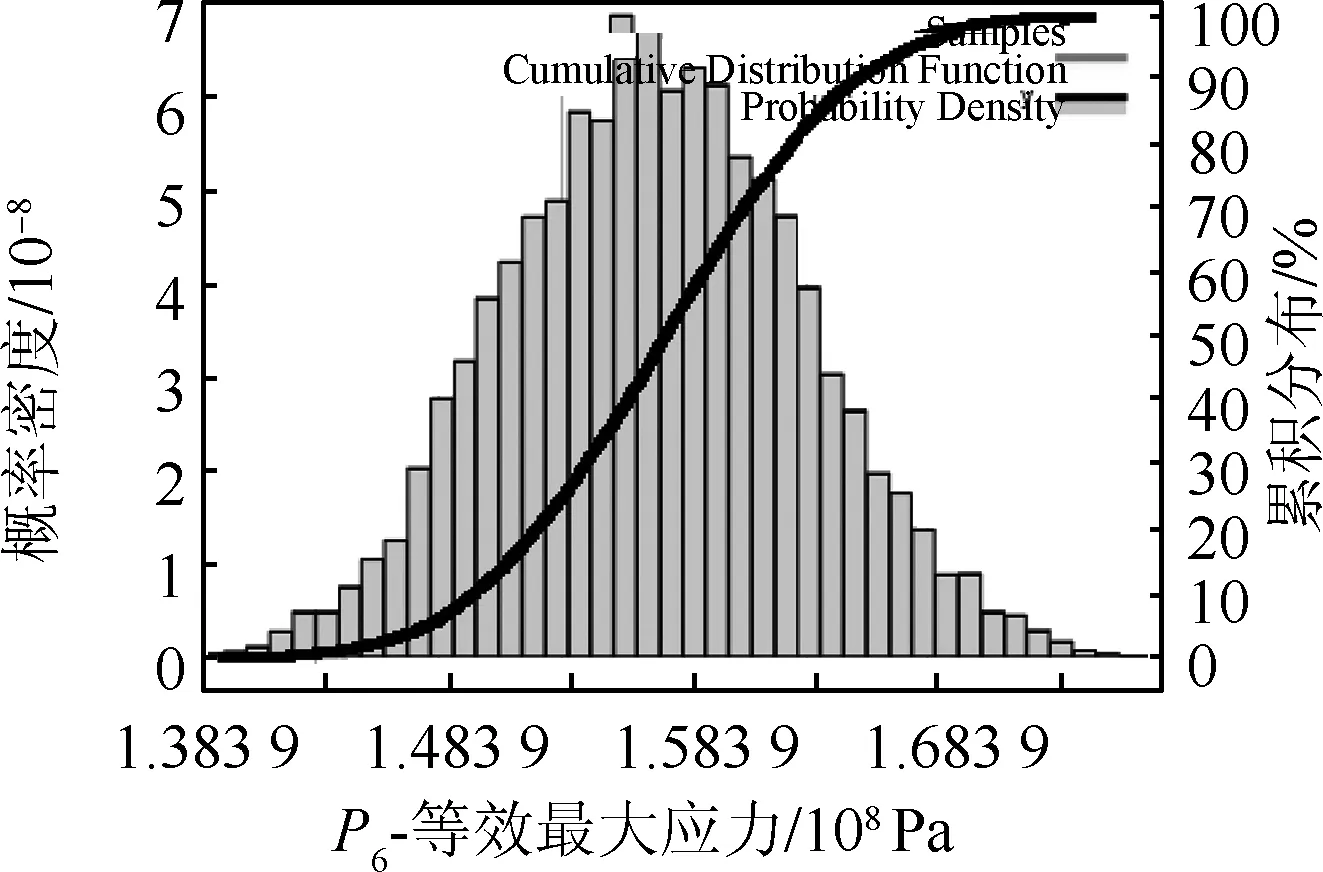
图7 等效最大应力拟合结果
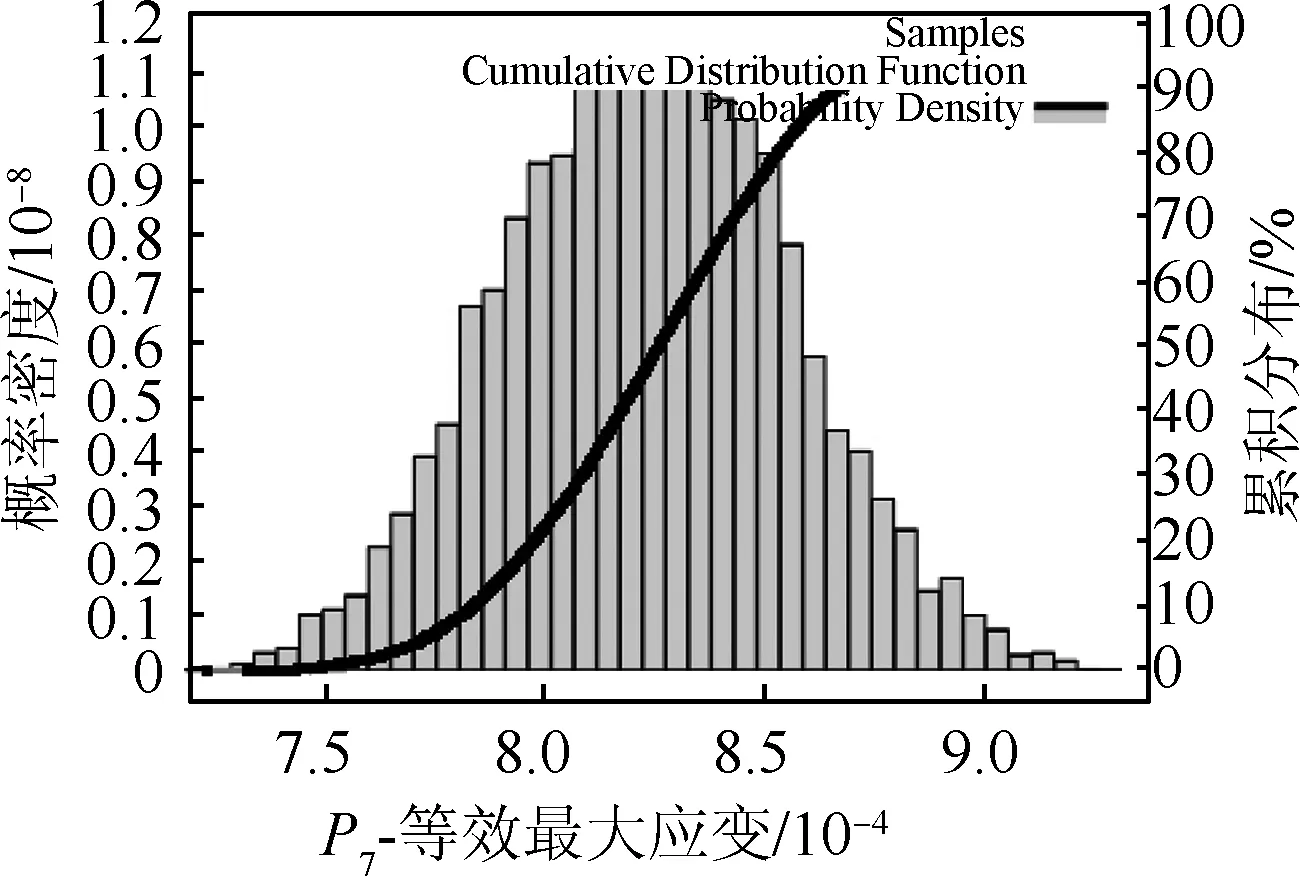
图8 等效最大应变拟合结果
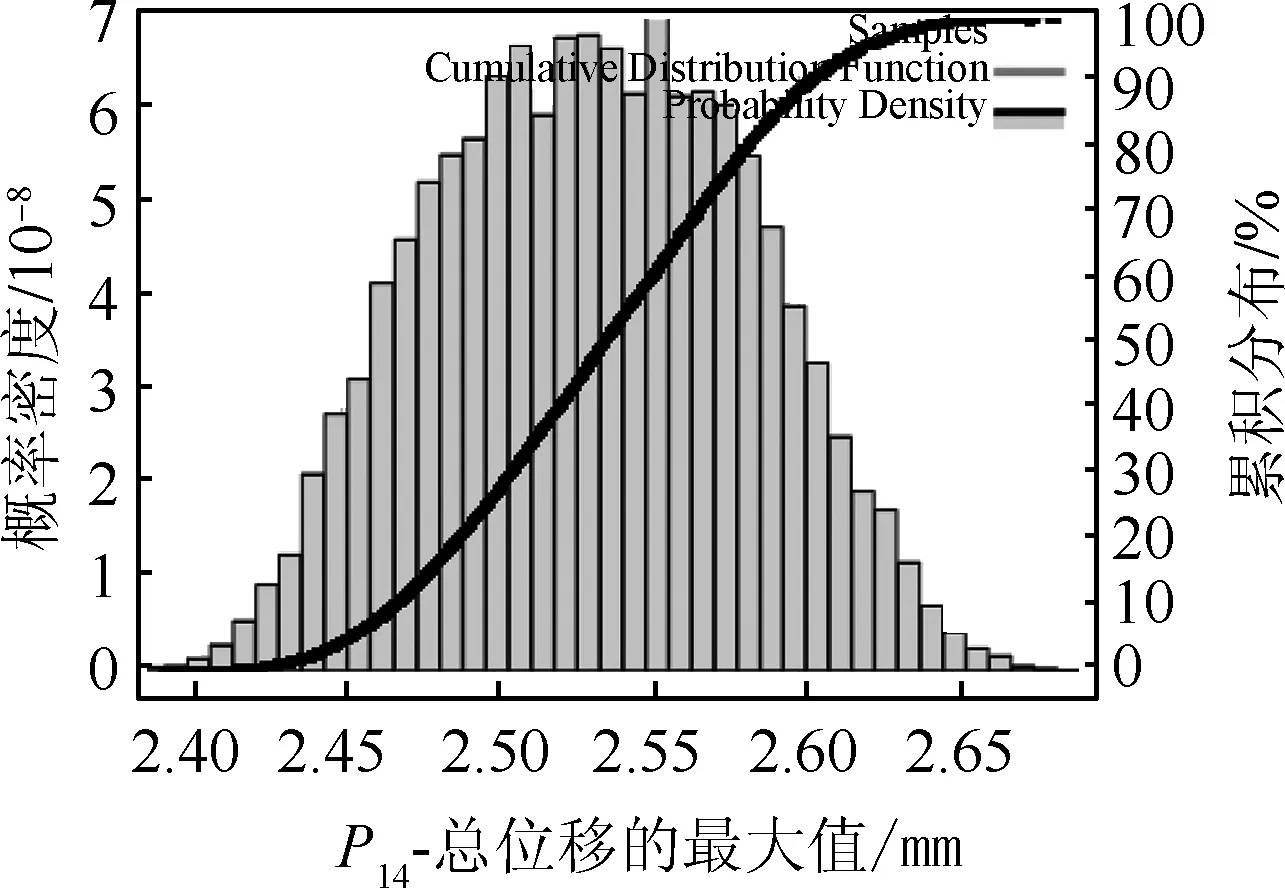
图9 总位移最大值拟合结果
P6、P7、P14的分布特征如表6所示。
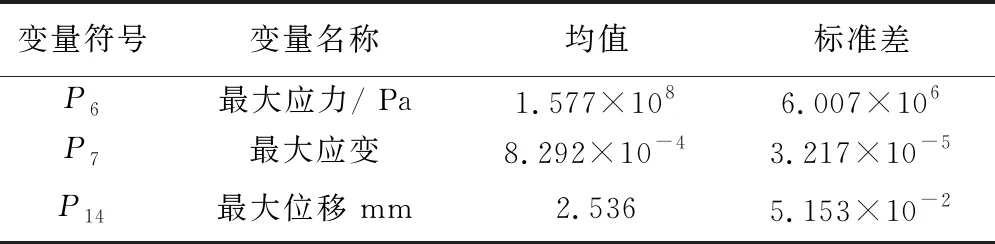
表6 不确定性分析结果
一个参数的灵敏度可定义为参数的变化对系统或结构产生的影响程度,因此通过参数灵敏度分析,能方便地找出最敏感的结构设计参数[12]。以工作环境下压紧弹簧的最大热应力为参数的响应指标,统计生成各输入变量对响应指标的影响效应大小(即参数灵敏度)如图10所示。

图10 灵敏度分析结果
由分析结果可知,对压紧弹簧所受热应力影响最大的变量是压紧载荷,灵敏度达到了0.6,并且为正向影响;其次为压紧弹簧的内、外径尺寸,分别呈现正向、负向的关系;弹簧中部高度有较小的负面影响;弹性模量、泊松比影响很小;上凸起、下凸起的高度几乎没有影响。
由于压紧弹簧所受的最大应力值与压紧弹簧的强度可靠性呈现负相关;因此压紧弹簧内径、弹性模量、泊松比、压紧载荷的增长均会导致压紧弹簧的可靠度下降,在实际工程设计与运行时应当控制。同时,可以适当提高弹簧的内径和弹簧中部高度以减小压紧弹簧所受的最大热应力。
4 结束语
本文通过对压紧弹簧进行热应力仿真,得到了压紧弹簧工作环境下的应力应变情况,并基于输入变量-输出变量的响应面模型,运用蒙特卡洛模拟,得出了仿真工况条件下的应力、应变、位移的分布特征,进行了灵敏度分析,为后续的参数优化设计提供了基础。
从灵敏度分析结果可知,压紧载荷对压紧弹簧的强度可靠性影响最大,压紧弹簧的内、外径尺寸次之,弹性模量、泊松比影响很小,上凸起、下凸起的高度几乎没有影响。在实际设计中可以适当提高弹簧的内径和弹簧中部高度,减小弹簧的外径并控制压紧载荷,以保证压紧弹簧的强度可靠性。
