SiC半导体不同晶面氧化机理及动力学的研究进展

赵春阳，王恩会，侯新梅

北京科技大学钢铁共性技术协同创新中心，北京 100083

近年来，世界各国都要求提高电力设备的效率以降低能源消耗. 尽管硅(Si)作为功率半导体器件已获应用，但受限于其物理特性，Si对功率器件性能的提升已达到极限. 碳化硅(SiC)是一种宽带隙半导体，相对于Si来讲，在功率器件应用中具有更优异的综合物理性能，如三倍宽带隙、三倍高导热性和10倍击穿电场等[1]. 此外，与Si类似，SiC也可以通过热氧化在表面生长二氧化硅（SiO2），该产物作为绝缘层在器件制造技术中具有重要的作用. 基于此，SiC已逐步取代Si成为功率器件的优选材料[2].

得益于SiC材料的上述优点，研究者对SiC在金属氧化物半导体场效应晶体管(MOSFET)中的应用进行了大量的探索[3−4]. MOSFET在结构上是以多晶硅−氧化物层（多为SiO2）−SiC或金刚石[5]为核心，这样的结构正好等同于一个电容器，中间的SiO2为电容器中介电质，而电容值由SiO2的厚度和介电系数决定. MOSFET广泛应用于模拟电路和数字电路中，作为栅极绝缘层的SiO2是通过SiC氧化形成的[6−9]. 在应用过程中SiC的通断电阻明显高于预期值且其通道迁移率非常低，这是由于不同SiC/SiO2界面处的氧化状态差异性造成的. 尤其对于非平面的MOSFET器件来说，SiC不同晶面取向上的氧化速率对其结构和性能有重要的影响[2]，因此了解SiC不同晶面取向上的氧化过程显得尤为重要.

动力学模型是认识和分析材料反应过程的有效工具. 但常规动力学模型都是从SiC整体来考虑氧化问题的，这样的处理无法揭示SiC不同晶面氧化的差异性. Deal-Grove模型是1965年Deal和Grove针对Si的氧化动力学研究建立的[10]，得益于对化学反应和扩散控速过程的综合考虑，该模型在金属和陶瓷材料等领域得到了推广应用.然而，SiC氧化时不同晶面存在各向异性且涉及到CO的外扩散，这与Si的氧化过程存在明显不同，因而Deal-Grove模型在描述SiC不同晶面的氧化过程时存在局限性.

近年来，很多学者通过对Deal-Grove模型进行改进[11−13]或建立新的氧化动力学模型[14−15]以期达到精确描述SiC不同晶面氧化过程的目的. 其中，Song模型[11]、Massoud经验关系式[12]和硅碳排放模型[15]是具有代表性且获得应用验证的. 本文将对上述三种模型进行重点介绍，并通过反应机理、模型预测曲线与实验数据的拟合情况两方面的研究对其优缺点进行比较，在此基础上，探讨了本课题组基于反应机理建立真实物理动力学模型应用的可能性，为精确描述SiC不同晶面氧化的动力学模型改进提供思路.

1 SiC 不同晶面取向的氧化动力学机理

研 究 表 明[11,16−17]，SiC 的 Si面和C 面氧化过程存在显著差异. Ito等[18]利用密度泛函理论对SiC不同晶面进行电子结构计算，用图例表示SiC的硅表面和碳表面的初始氧化过程.图1是SiC的C面和Si面与O结合的过程示意图[18].从图1（a）～（d）可以看出，氧气进入C面后会替换表面最上层的C原子形成三配位O原子（图1（b）所示）. 随后形成SiO−C键，经历重排后稳定为Si−O 键，形成了如图 1（c）所示的具有两个 Si−O 键的局面. 随着最上层的C原子逐渐被取代，最终形成图1（d）的类SiO2层. 不同于C面，氧气进入Si面后（图 1（e）～（h）），O 原子优先与吸附的 Si原子和最上层 Si原子结合，形成 Si−O−Si键（图 1（f）所示）. 随着O原子的增多，第二层其中的一个C原子解吸、O原子吸附在表面弥补位置，从而形成四配位O原子（图1（g）所示）. 随着O原子的进入，逐渐形成 SiO−C 键、Si−O 键、Si−Si键，最终形成 Si−O−Si结构，如图 1（h）所示.

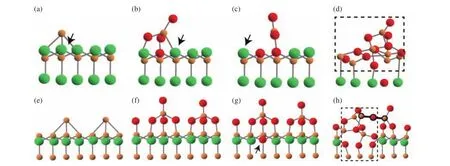
图1 SiC的C面和Si面O结合表面的侧面图（红色原子表示O原子，橙色原子表示Si原子，绿色原子表示C原子）[18]. （a～d）C面随着氧气含量递增的氧化过程；（e～h）Si面随着氧气含量递增的氧化过程Fig.1 Side views of typical configurations of O-incorporated surfaces on the C-face and Si-face of SiC (Orange, green, and gray circles denote Si, C, and H atoms, respectively) [18]: (a−d) the oxidation process of the C-face with increasing oxygen content; (e‒h) the oxidation process of the Si-face with increasing oxygen content

上述观点在Matsushita的工作中也得到验证[19].Matsushita发现碳在硅表面和碳表面的湮灭过程有很大的差异：在C面上，碳原子以0.7 eV的离解势垒直接与底物分离为CO分子. CO分离后，界面处出现了3倍的协调氧原子且保留高密度的C悬键；在Si面上，C原子在界面上形成碳纳米团簇（有几个原子构成，有单键也有双键），界面处的悬键数量较C面少. 在分子动力学 (MD) 模拟中，CO分子以2.8 eV的离解势垒从碳纳米团簇中分离. 在Si面和C面上CO形成过程中，由于形成过程不同、离解势垒相差较大，导致Si面和C面的氧化过程存在显著差异.

2 Deal-Grove 模型及其改进模型

2.1 Deal-Grove 模型

Deal-Grove模型突破了先前模型在反应过程中将界面反应和扩散过程割裂考虑的局限[10]. 基于对Si反应本质的认识，实现了对上述反应步骤的综合考虑，提出了氧化物的生长遵循如下关系：

其中，X是氧化物厚度，t是氧化时间，τ是初始阶段Si在薄氧化区（X<0.05 μm）氧化的时间，与初始厚度有关. Deal-Grove模型同时考虑了氧化过程前期化学反应的控制速率步骤和后期扩散反应控制速率步骤（图2），将前期受化学反应速率控制的氧化过程定义为线性增长过程，其速率常数为B/A；将后期受扩散速率控制的氧化过程定义为抛物线增长过程，其速率常数为B.

图2 Deal-Grove定义的线性−抛物线时间规律的动力学过程[20]Fig.2 Dynamics process of the linear−parabolic time law defined by Deal-Grove[20]

基于此，Deal-Grove模型在其提出的很长一段时间内，广泛应用于不同材料氧化行为的描述. 但Deal-Grove模型在应用于描述SiC氧化过程时[21−22]，发现模型计算结果与实验数据吻合度不高，尤其是氧化厚度小于20 nm时，SiC中C面和Si面的氧化物生长速率比Deal-Grove模型给出的预测结果要高得多. 分析发现，一方面，针对Si的氧化建立的Deal-Grove模型没有考虑反应过程产生的气体产物对反应的影响，而这在处理SiC氧化过程中是不可忽略的；另一方面，SiC氧化速率对晶面取向的依赖性也远远大于Si[16−17]. 因此在描述SiC不同晶面氧化规律方面，Deal-Grove模型的改进研究得到了广泛关注.

2.2 Song 模型及应用

Song模型[11]用气体进入氧化层的速率表达SiO2的生长速率，同时考虑了SiC氧化过程中气体产物的外扩散过程. 如图3所示，SiC氧化过程可以分为五个步骤：

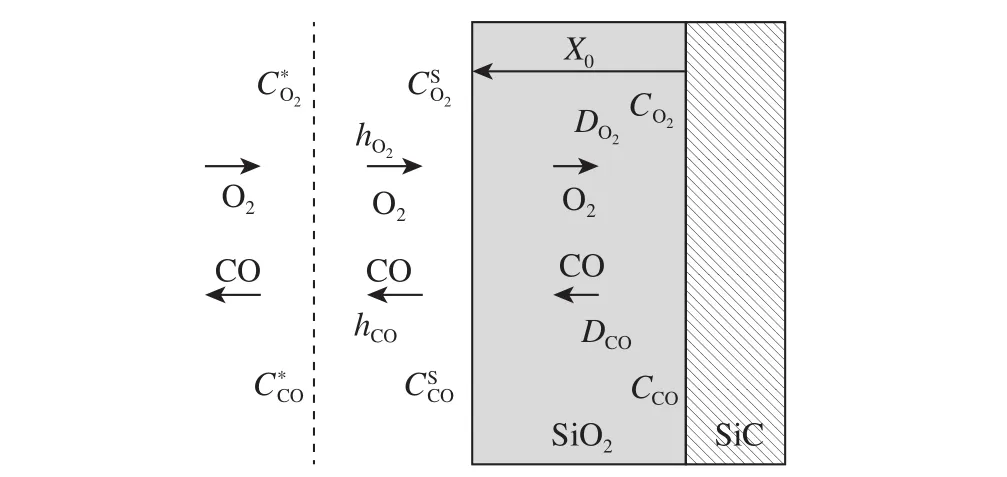
图3 考虑气体产物外扩散的SiC氧化示意图[11]Fig.3 Schematic of SiC oxidation considering external diffusion of gas products[11]

（1）氧气输送到氧化物表面；

（2）氧气通过氧化膜扩散；

（3）在氧化物/SiC界面处与SiC反应；

（4）产物气体通过氧化膜向外扩散；

（5）产物气体从氧化物表面向外逸出.

通常认为上述过程中第（1）步和第（5）步不太可能是氧化过程的限速步骤，因此需要考虑第（2）、（3）、（4）步中的进入和逸出的气体通量问题.氧化物层的增长速率和气体通量的关系可以用下式表述：

将公式（2）和 Deal-Grove模型方程（公式（1））进行联立得到系数A和B. 在SiC的热氧化过程中，氧气流向氧化产物表面的过程通常不作为一个限速步骤考虑，所以或者两者兼而有之. 同时在氧化过程中，. 根据以上条件可以得到线性速率常数B/A和抛物线速率常数B的表达式：

其中，Kf，Kr分别是正向反应速率常数、反向反应速率常数.

Song模型中详细地表述了以下三种情况时速率常数的表达式：

①在线性增长过程中，如果界面反应是限速步骤，则线性速率常数B/A的表达式为：

②在抛物线生长的过程中，扩散过程可能是反应的限速步骤. 如果氧的内扩散是限速步骤，则抛物线速率常数B的表达式为：

③如果CO的外扩散是限速步骤，则抛物线速率常数B的表达式为：

可见，Song模型在Deal-Grove模型的基础上，丰富了SiC氧化过程中抛物线生长行为占主导地位时限速步骤的可能性，即不再只是氧的内扩散，还有可能是CO的外扩散. SiC不同晶面的氧化可能存在其中一种或两种扩散，模型详细表述了两种扩散作为限速步骤时的速率常数，为描述不同晶面的氧化过程提供了方案. 基于此，Song模型可以更准确地描述和预测SiC的氧化行为[23−24].

基于上述优点，Song模型在描述4H-SiC晶片的不同晶面氧化行为方面已进行应用[11]. 实验中采用的是沿方向切割抛光成约为5 mm×5 mm的SiC晶片（n型）. 清洗后，立即将晶片装入氧化炉中，在常压和氧流量为1 L·min−1的条件下进行不同温度（950～1150 ℃）的氧化处理. 取1050～1150 ℃的实验数据与Song模型计算曲线作图4. 从图4（b）中可以看出，Song模型针对C面的计算结果与实验数据取得较好拟合，拟合数据与实验数据之间的误差约为3.1%，而Si面上的计算结果与实验数据出现一定偏差，误差约为7.2%（图4（a））. Song模型没有考虑到Si面的氧化初期存在非稳态增长的情况，这应该是造成了该模型在描述Si面氧化行为时误差较大的主要原因.

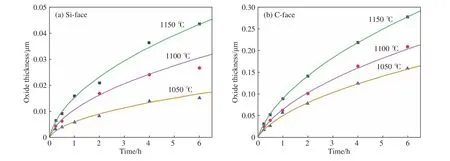
图4 Song模型计算结果（实线）和4H-SiC氧化实验结果[11]（散点）对比图. （a）Si面氧化物的厚度与时间和温度的函数关系；（b）C面氧化物的厚度与时间和温度的函数关系Fig.4 Comparison of calculation results of the Song model (solid curves) and experimental results of 4H-SiC oxidation[11] (scatters): (a) oxide thickness as a function of time and temperature for dry thermal oxidation of the Si-face of 4H-SiC; (b) oxide thickness as a function of time and temperature for dry thermal oxidation of the C-face of 4H-SiC

2.3 Massoud 经验关系式及应用

根据Deal-Grove模型，氧化发生在SiO2/Si界面，由氧气扩散到界面处与Si反应. 但Si在SiO2厚度很薄时（X<0.05 μm）的生长速率与Deal-Grove模型预测的结果相差较多[21−22]. 所以Massoud等将初始阶段的Si氧化视为非稳态过程[12]，在Deal-Grove模型的基础上增加了一个描述初始增长速率的系数得到了Massoud经验关系式. Massoud经验关系式是将公式（1）重写为微分形式并添加一个指数项：

Goto等发现Massoud经验关系式与传统的Deal-Grove模型相比，对SiC氧化过程的曲线拟合效果更好[13]. 同时发现SiC的C面，a面和Si面的氧化活化能之比接近1∶2∶3. 如图5所示，当SiC衬底表面上的Si原子被氧化时，C面上有一个Si−C键要被破坏，a面上有两个Si−C键要被破坏，Si面上有三个Si−C键要被破坏. 因为活化能的比例与晶面取向之间断裂的Si−C键数的差异相同，所以限速界面反应中的氧化活化能应与晶面上破坏的Si−C键键能有关. 因此，在实验中可以通过计算不同晶面氧化时的活化能，来判断当前的氧化速率受哪一晶面上的氧化反应影响，进而确认反应的限速步骤. 此外，运用Massoud经验关系式时，如果测量更加密集的生长速率数据，可以得到更精确的生长速率曲线和合适的氧化速率参数[25]，被用作4H-SiC氧化的高精度二维和三维模拟[2].

图5 不同晶面 Si–C 键氧化过程演变示意图（橙色箭头表示 Si背键）[13]. （a）Si面；（b）a 面；（c）C 面Fig.5 Schematics of Si–C bonds on the SiC surface (the orange arrow denotes a Si back-bond)[13]: (a) Si-face; (b) a-face; (c) C-face

Goto等[13]以4H-SiC的Si面（n型，偏离轴心8°）和 C 面（n 型，偏离轴心 0.5°）为研究对象，在温度区间为 900～1200 ℃、氧流量为 1 L∙min−1、氧分压为1.01325×105Pa的条件下进行氧化实验. 取900～1150 ℃部分实验结果与Massoud经验关系式计算曲线作图6. 在图6中可以看出，Massoud经验关系式在Si面的预测曲线与实验数据的拟合程度比Song模型要好，误差值约为4.9%. 这是因为Massoud经验关系式考虑了氧化初始阶段的生长速率非稳态增长现象，更加符合SiC氧化前期的特点. 而Massoud经验关系式在C面的预测曲线与实验数据的拟合程度却出现误差比Song模型大的情况，约为8.1%. Massoud经验关系式只引入了氧化初始阶段的非稳态问题，但并没有考虑CO的外扩散，这很有可能是导致其在描述C面氧化时误差值变大的原因.

图6 Massoud经验关系式计算结果（实线）和4H-SiC氧化实验数据[13]（散点）对比图. （a）不同温度下Si面氧化层的厚度与氧化层生长速率的函数关系；（b）不同温度下C面氧化层的厚度与氧化层生长速率的函数关系Fig.6 Comparison of calculation results of the Massoud empirical relation (solid curves) and experimental results of 4H-SiC oxidation[13] (scatters):(a) oxide thickness dependence of the oxide growth rate at various temperatures on the Si-face of SiC; (b) oxide thickness dependence of the oxide growth rate at various temperatures on the C-face of SiC

3 硅碳排放模型及应用

在上述基于Deal-Grove模型的两种改进模型中，C的氧化及排放和Si的前期非稳态氧化无法同时兼顾. 为解决这一问题，Kageshima等[14]、Hijikata等[15]建立了新的氧化动力学模型，即硅碳排放模型. 图7为硅碳排放模型示意图，其中C、x和X分别表示浓度、到界面的距离和氧化层厚度，、分别表示Si在氧化层表面和氧化层内部的反应速率，、分别表示C在氧化层表面和氧化层内部的反应速率. 下标Si、C、O表示对应原子的值.

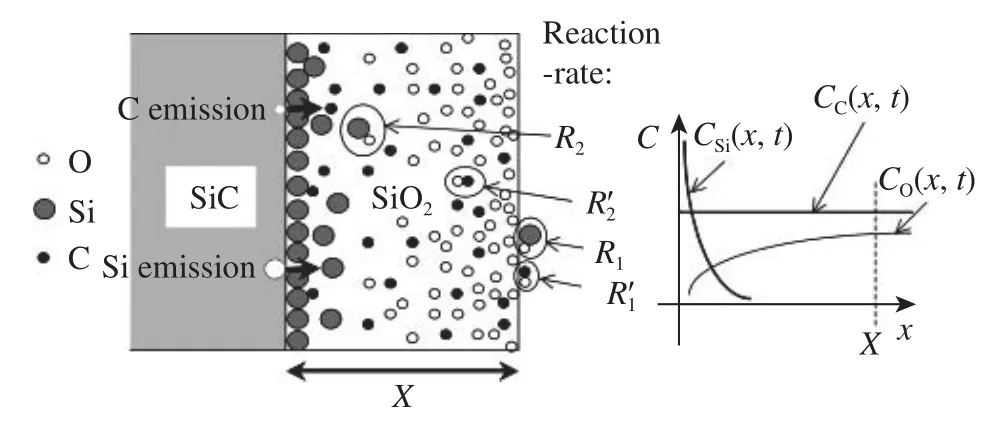
图7 硅碳排放模型示意图[15]Fig.7 Schematic illustration of the Si–C emission model [15]

考虑到氧化过程中界面释放的Si和C原子以及C的氧化过程，SiC的氧化反应可以写成：

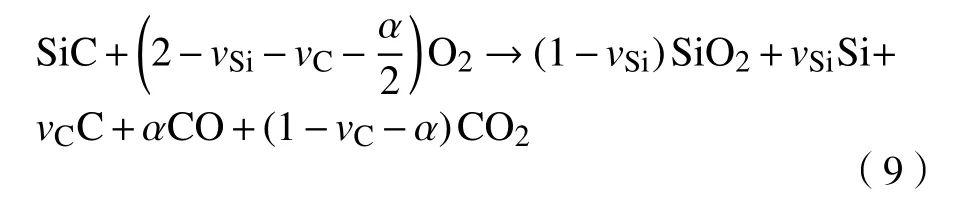
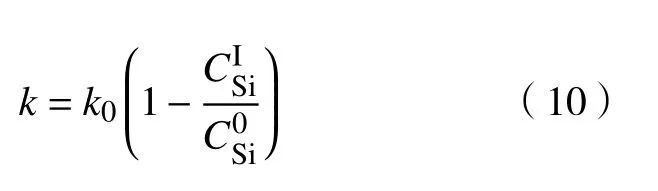
在结合了Si和C的排放、CO和O的扩散等过程之后，硅碳排放模型将氧化速率描述为：

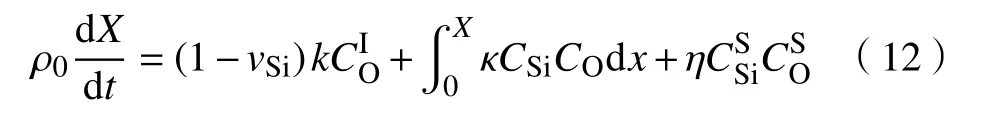
硅碳排放模型对于SiC氧化过程的描述得到了很好的验证[25]. 验证实验中采用的SiC样品，其预处理方法以及实验温度均与上述Massoud经验关系式的验证实验一致. 选取实验中900～1150 ℃的数据与硅碳排放模型计算曲线作图8. 计算结果表明，硅碳排放模型比前面两种改进模型的误差都要小，即Si面、C面的误差分别为4.86%和3.79%.这说明硅碳排放模型更好地综合考虑了CO扩散和Si的前期氧化非稳态过程. 但是，硅碳排放模型存在表达式过于繁琐的问题，这使其在应用方面受到限制.

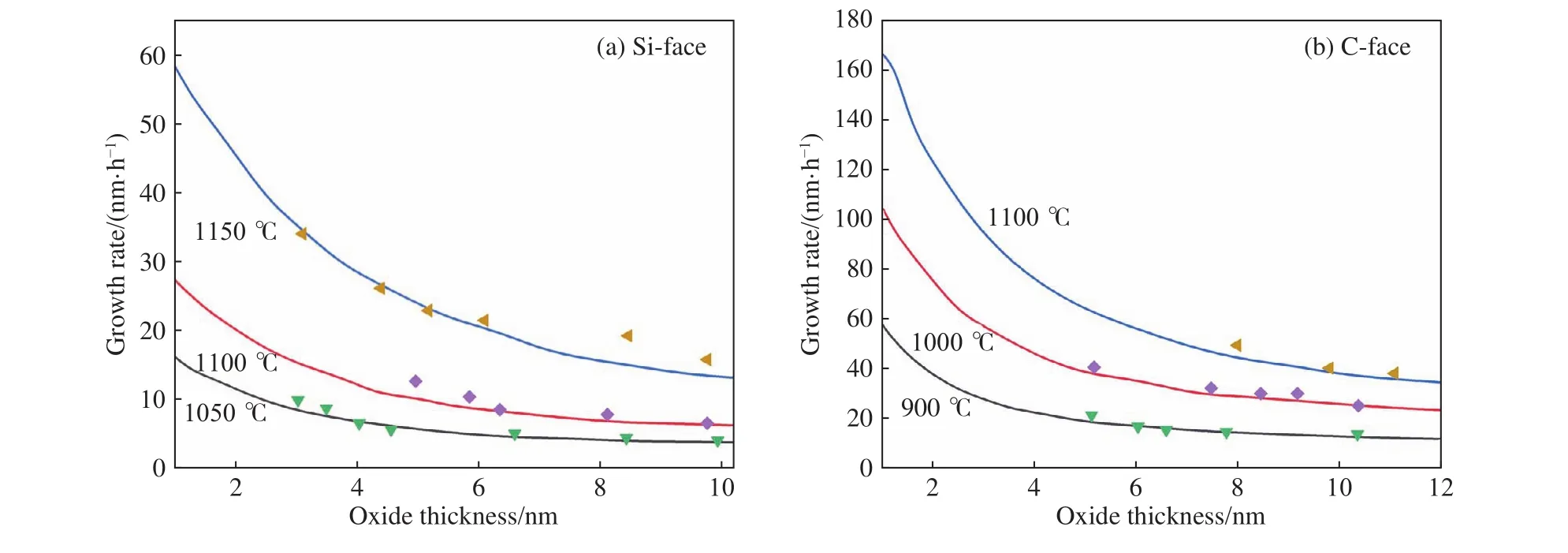
图8 硅碳排放模型的计算结果（实线）和4H-SiC氧化实验数据[25]（散点）对比图. （a）不同温度下Si面氧化层的厚度与氧化层生长速率的函数关系；（b）不同温度下C面氧化层的厚度与氧化层生长速率的函数关系Fig.8 Comparison of calculation results of the “Si and C emission model” (solid curves) and experimental results of 4H-SiC oxidation[25] (scatters):(a) oxide thickness dependence of the oxide growth rate at various temperatures on the Si-face of SiC; (b) oxide thickness dependence of the oxide growth rate at various temperatures on the C-face of SiC

4 模型应用效果的对比

为进一步验证上述三个模型的有效性，选取Gupta和Akhtar[26]研究中4H-SiC的Si面氧化数据（实验选取美国M/s CREE研究公司的2英寸的n型4HSiC在1050～1150 ℃的温度区间下进行）与各个模型计算结果进行对比，其结果如图9所示. 从图9（a）中可以看出，Song模型由于没有考虑Si初期氧化的非稳态情况，因而在Si面上的计算曲线与实验氧化数据相差较大，这与前文提到的情况一致. Massoud经验关系式和硅碳排放模型的计算结果误差都较小，分别为4.65%、4.07%. 这再次验证了同时考虑CO外扩散和Si的前期氧化非稳态氧化过程的硅碳排放模型在准确描述SiC晶面氧化行为方面的优势.

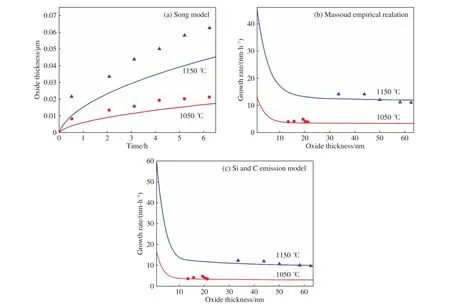
图9 Gupta[26]研究中 4H-SiC 的 Si面氧化数据（散点）与三个模型的计算结果（实线）对比图. （a）Song 模型；（b）Massoud 经验关系式；（c）硅碳排放模型Fig.9 Comparison of the Si surface oxidation data of 4H-SiC in the Gupta[26] study (scatter point) and the calculation results of the three models (solid curves):(a) Song model; (b) Massoud empirical relation model; (c) silicon carbon emission model

5 氧化动力学模型的发展方向

笔者所在课题组在之前的研究[27−30]中，建立了参数物理意义明确且具有显函数表达特征的真实物理动力学模型（Real physical picture, RPP）模型. 该模型能够准确揭示氧分压、材料粒度及材料维度等因素对非氧化物陶瓷在恒温和变温环境下氧化行为的影响. 此外，RPP模型可以通过一次线性回归就可以准确计算出反应的活化能和特征氧化时间，其处理过程相对简单且准确度高. 得益于上述优点，RPP模型在非氧化物陶瓷和其他材料领域（碳复合材料、合金等）已取得广泛应用.在描述SiC晶面的氧化过程时，可将其视为薄样块氧化处理. 当界面反应为控速步骤时，RPP模型对应的表达式为：

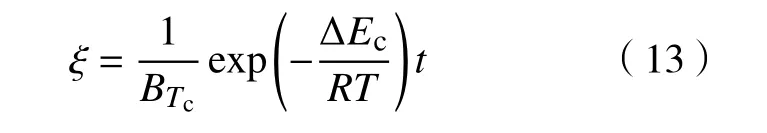
当扩散步骤为控速步骤时，RPP模型对应的表达式为：

需要指出的是，已有模型均是基于SiC的惰性氧化过程建立. 当在特定条件下，SiC发生活性氧化时（产物为挥发性的SiO），不同晶面的氧化行为和规律会发生明显变化，相关的动力学模型有待进一步建立和优化.

6 结论

基于动力学模型来准确描述SiC不同晶面的氧化规律，对其在金属氧化物半导体场效应晶体管中的应用至关重要. 通过对Song模型、Massoud经验关系式和碳硅排放模型的改进方法和应用结果的比较分析，得出了下列结论：

（1）Song模型在预测SiC不同晶面氧化时考虑到CO的外扩散使改进后的模型预测曲线与实验结果拟合度更高. 无论是通过理论推证还是实验数据曲线都可以得到SiC的不同晶面生长速率存在各向异性. 但Song模型由于未考虑Si面氧化前期存在非稳态增长的情况，因此在Si面上的预测结果误差较大.

（2）Massoud经验关系式考虑了SiC氧化初始阶段的生长速率非稳态增长的现象，更加符合SiC氧化前期的特点，因而对于Si面的氧化过程的预测与实验数据达到了很好的吻合. 但Massoud经验关系式只考虑了初始生长速率的变化，实际氧化过程中碳的氧化和排放以及硅的排放是不能忽略的.

（3）碳硅排放模型同时考虑了Si和C的氧化及排放，在这种情况下很好地预测了SiC不同晶面的氧化过程. 但因为其考虑的方面较多，造成模型表达式复杂，在实用性方面存在局限性.

（4）笔者所在课题组建立的RPP模型在描述SiC不同晶面氧化方面具有较大潜力. 此外，在活性氧化时SiC不同晶面的氧化行为会发生明显变化，相关氧化动力学模型有待进一步建立和优化.