基于鲁棒H∞滤波的锂离子电池SOC估计

潘凤文，弓栋梁，高 莹✉，寇亚林

1) 吉林大学汽车仿真与控制国家重点实验室，长春 130025 2) 吉林大学汽车工程学院，长春 130025

锂离子电池能够提供较高的能量密度和比功率，没有记忆效应，具有较低的自放电率和较长的可循环使用寿命，且后续回收过程中对环境污染相对较少，这些特性使其成为目前新能源汽车的重要动力源[1−3]. 但随着锂离子电池在新能源汽车中进一步广泛而深入的使用，其可靠性和安全性正在受越来越严苛的考验. 电池管理系统（Battery management system，BMS）的核心目标就是获得表征锂电池可用容量的SOC，保证电动车辆安全有效的运行，并通过降低电压极限的不确定性来实现动力分配的优化，从而延长电池的使用寿命[4−6].然而，目前锂离子电池可用的测量是电流、电压和温度，SOC不能直接测量[7−8]. 因此，准确估计SOC对保证锂电池的安全性和可靠性至关重要.

对于锂离子电池SOC的估计方法，目前可大致分为两类：无模型法（安时积分法、开路电压法）和基于模型的方法[9−13]. 基于模型的SOC估计中，常用的建模方式有黑箱模型、电化学模型、等效电路模型等. 黑箱模型通常使用传递函数来描述电池的行为，无需重建其基本的物理化学过程，但是该模型应用场景受限，且模型精度不高. 电化学模型采用一组偏微分方程来构建整个物理化学过程的“时−空”动态变化，该模型中大量复杂的电化学方程计算耗时长，主要用于优化电池的物理设计和电池相关的设计参数，表征电能产生的基本机理等. 等效电路模型一般可分为Thevenin模型和阻抗模型两大类. 这些基于电压源，电阻和电容组合的模型具有直观、实用和易于处理的特点，通常用于控制设计，且特别适合与其它电路或系统进行协同设计和协同仿真. Thevenin模型又可分为一阶RC等效电路模型，考虑电压滞后的增强自校正模型，以及二阶和高阶RC模型等.

在有关实时获取电池SOC的文献中，广泛采用基于模型的SOC估计方法进行研究. 文献[14]采用二阶RC等效电路模型，结合安时积分法与基于模型的方法对锂电池的SOC进行估计，其结果表明，该方法增强了对测量噪声的鲁棒性. 文献[15]～[16]针对离散化的锂离子电池二阶RC等效电路模型，采用线性参变技术，设计了计算资源需求较少的SOC估计器，而且其所设计的估计器的稳定性可由线性矩阵不等式（Linear matrix inequality，LMI）技术来分析验证. 文献[17]采用大电容二阶RC电池模型，该模型可用状态空间函数来表示，由大容量电容的电压值和电容值来确定SOC. 并在此模型基础上设计了对未知扰动和模型不确定性具有一定鲁棒性的H∞滤波器；其所设计的H∞滤波器对SOC具有很好的估计性能. 文献[18]采用与文献[17]中相同的等效电路模型，相较于文献[17]，文献[18]中设计了能够改善观测器响应速度的H∞切换观测器，进一步提升了对SOC的估计性能. 文献[9]和[19]均采用电化学锂离子电池模型，并基于该模型设计了用于估计SOC的具有常值增益的龙伯格非线性观测器，以及一个改进的输出雅可比矩阵加权增益的非线性观测器，其中观测器增益的设计均被转化为了求解LMI问题.文献[20]采用二阶RC等效电路模型，把电池老化建模为加性故障，并对锂离子电池模型进行了线性化，设计了基于H∞观测器的故障估计器，从其仿真结果来看，所设计的故障估计器对干扰具有很好的鲁棒性，同时对老化故障具有很强的追踪能力. 文献[21]采用与文献[20]中相同的锂离子电池模型，针对SOC的估计问题，采用LMI技术设计了基于H∞方法的非线性观测器. 文献[22]针对锂离子电池SOC的估计误差收敛问题，设计了三种基于LMI技术的鲁棒龙伯格SOC观测器，并分别与传统的基于非线性等效电路模型的扩展卡尔曼滤波器进行对比，对比结果表明，其设计的两种基于LMI的SOC观测器与广泛使用的扩展卡尔曼滤波器具有相近的性能，并且设计方法更为简单. 文献[23]～[24]均采用非线性分数阶锂离子电池模型对SOC进行估计，不同之处是前者采用二阶RC等效电路模型，并基于SOC估计误差动力学方程，运用LMI技术来设计SOC观测器；后者采用基于阻抗模型和分数阶卡尔曼滤波方法对SOC进行估计.

综上可知，大多数文献在锂离子电池SOC估计中选择与LMI技术相结合，这样不仅可以简化设计过程，而且也保证了SOC的估计准确性和一定的鲁棒性. 然而，针对锂离子电池模型参数随温度变动而产生摄动，进而影响SOC估计准确性的问题讨论的并不多. 因此，本文在前述工作基础之上，考虑电池温度波动对模型参数的影响，把温度对模型参数的影响方式建模为标称电阻值和电池总容量的加性变量，并视温度变化为系统的外部扰动. 然后，采用切线法对模型进行线性化. 继而采用LMI技术设计了对SOC进行估计的鲁棒H∞滤波器. 最后，采用四种不同类型的动态激励电流，并与kalman滤波对SOC的估计进行对比，对所设计的SOC观测器进行验证.

1 锂离子电池建模

锂离子电池的动态特性高度依赖于它的工作条件，具有时变参数的二阶RC等效电路模型可以足够精确的来表征锂电池系统特性，同时又相对简单且计算量不大. 因此，本文主要采用二阶RC等效电路模型.

1.1 电气模型

表征锂离子电池动态特性的二阶RC等效电路模型如图1所示.

图1 等效电路模型Fig.1 Equivalent circuit model

根据基尔霍夫电压定律，锂离子电池的二阶RC等效电路模型的动力学方程可表述为

式中：t代表时间，s；Uocv代表与SOC相关的开路电压（其为SOC的函数），V；Ic为进入或离开电池正极的电流（放电时为正，充电时为负），A；R0为内阻，Ω；R1和C1分别为电化学极化电阻（Ω）和电容（F）；R2和C2分别为浓差极化电阻（Ω）和电容（F）；U1和U2分别代表电化学极化电容C1和浓差极化电容C2的电压，V；UT为端电压，V.

1.2 电池荷电状态模型

电池SOC的定义为可用容量（A·h）与电池的总容量的比值. 简化的SOC估计模型如下：

式中，Q为电池总容量，SOC0为电池的初始SOC.需要指出的是电池容量也会随着温度的升高而变化，从而影响SOC估计的准确性[13].

大量试验表明，开路电压Uocv与SOC在较大的工作区间内均存在一定的线性关系（除了SOC非常高或非常低的情况，小于20%或大于80%）[14−15].因此，可以在特定的工作范围采用SOC的线性函数来近似逼近开路电压. 它们之间的函数关系具有以下形式：

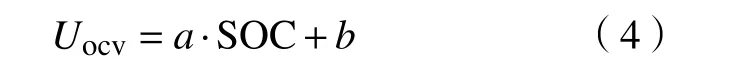
式中：a和b为给定的常量.

那么根据公式（4），终端电压UT与SOC的关系可表示为：

所选用的电池模型参数如下表1所示[20]. 该模型参数的获取需要满足以下的条件：（1）T=40 ℃，Ic=1 A，SOC=0.5；（2）电池模型的参数与温度、SOC、以及电流的大小和方向均无关.

表1 电池模型参数Table 1 Battery model parameters

上述条件假设非常严格，大量的实际实验已表明：电池模型参数对于诸如温度、SOC和充放电状态以及电流等环境状况的变化是很敏感的；其中，温度对电池模型参数的影响最为显著[16].

2 模型线性化

由于温度对锂离子电池的模型参数具有较大的影响，因此，本文将温度对模型参数的影响方式建模为标称电阻值和电池总容量的加性变量. 其具有如下形式：

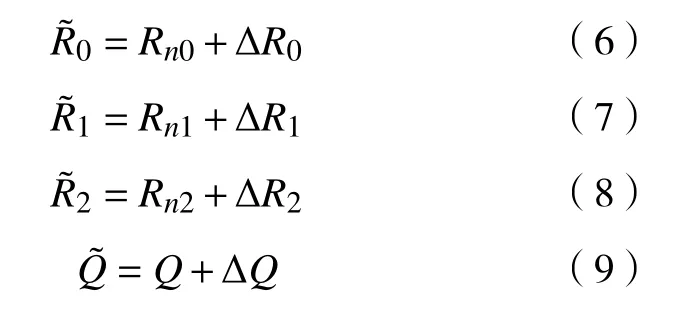
式中：Rni(i=0,1,2)分别表示，，标称阻值；ΔRi(i=0,1,2)表示由温度变化而引起的阻值变化；R˜i(i=0,1,2)表示由温度变化而产生的最新阻值；表示由温度变化引起的电池容量变化，表示由温度变化产生的最新容量.

3 鲁棒 SOC 估计器设计

针对线性化系统（15），设计一个渐近稳定的H∞滤波器，实现对SOC的估计，使得传递函数（从外部扰动到SOC估计误差）的H∞范数小于给定值，该滤波器具有以下状态空间形式:

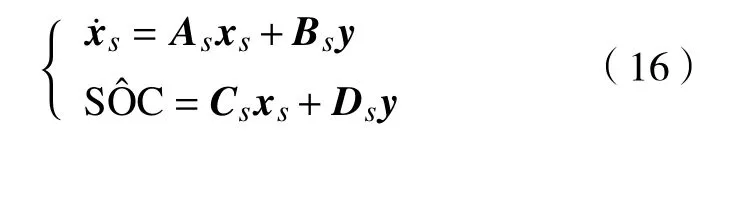
4 仿真实验

通过在Matlab中求解优化问题（29），获得干扰抑制性能指标 γ =5.7274×10−5. 最终获得所设计的鲁棒H∞滤波器状态空间矩阵分别为

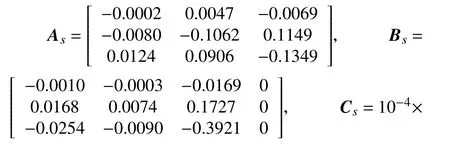
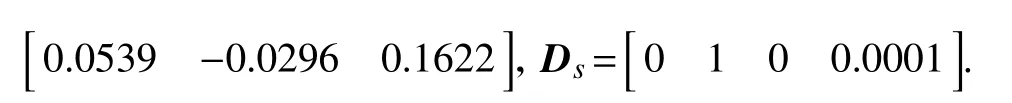
仿真实验中给电流输入信号注入了能量为0.001的白噪声，温度变动用幅值为40的正弦函数进行模拟，仿真结果与kalman滤波对SOC的估计结果进行对比分析. 采用四种类型的动态测试进行仿真实验验证，其分别为 BJDST (Beijing Dynamic Stress Test)、FUDS (Federal Urban Driving Schedule)、US06 (US06 Highway Driving Schedule)以及 BJDST−FUDS−US06联合驾驶时间表动态测试. 一个完整BJDST 循环是 916 s，一个完整 FUDS 循环是 1372 s，一个完整US06循环是600 s. 其完整循环时间历程如下图2，图3所示.

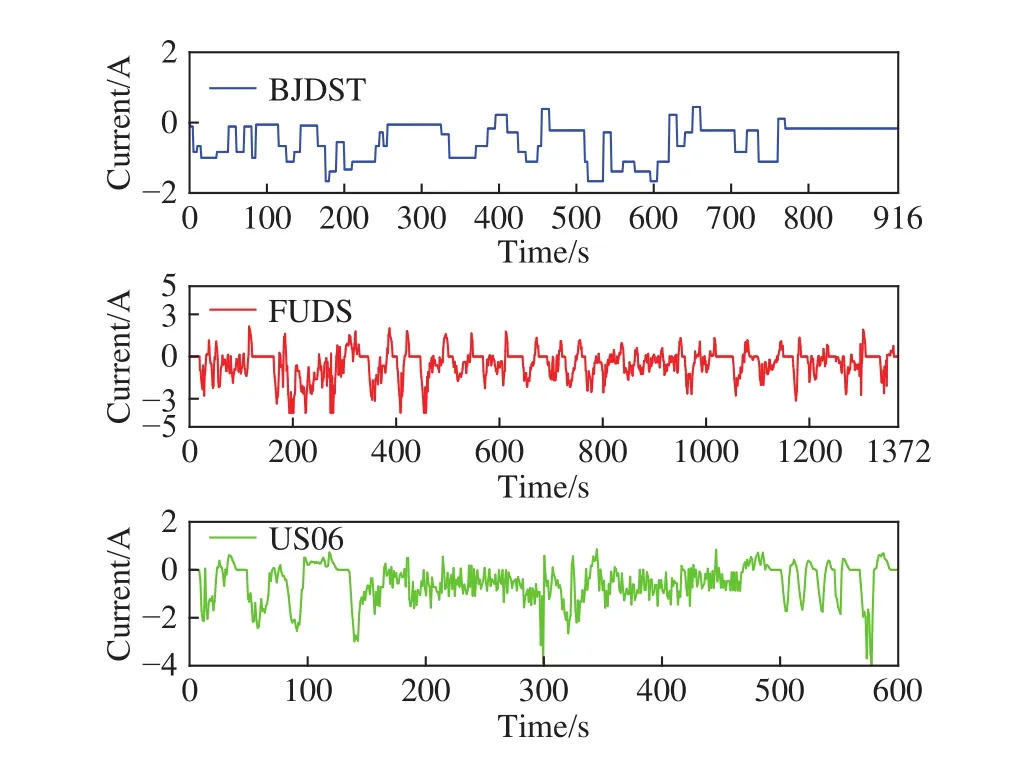
图2 BJDST，FUDS，US06动态测试时间历程Fig.2 BJDST, FUDS, US06 dynamic test time history

图3 BJDST−FUDS−US06联合动态测试时间历程Fig.3 BJDST−FUDS−US06 joint dynamic test time history

BJDST，FUDS和US06动态激励下的基于H∞滤波的SOC估计和基于kalman滤波的SOC估计以及它们的SOC估计误差时间历程曲线如图4～图9所示. 其中蓝色实线表示模型输出，红色实线表示H∞估计，绿色实线表示kalman估计.

图4 BJDST 激励的 SOC 估计Fig.4 SOC estimation excited by BJDST

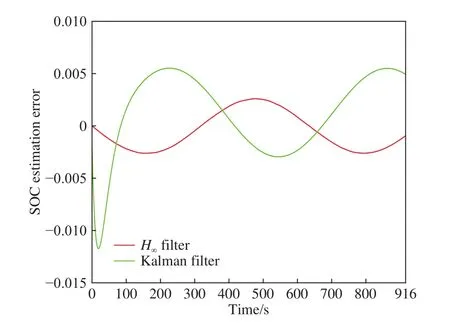
图5 BJDST 激励的 SOC 估计误差Fig.5 SOC estimation error excited by BJDST

图6 FUDS 激励的 SOC 估计Fig.6 SOC estimation excited by FUDS

图7 FUDS 激励的 SOC 估计误差Fig.7 SOC estimation error excited by FUDS

图8 US06激励的 SOC 估计Fig.8 SOC estimation excited by US06

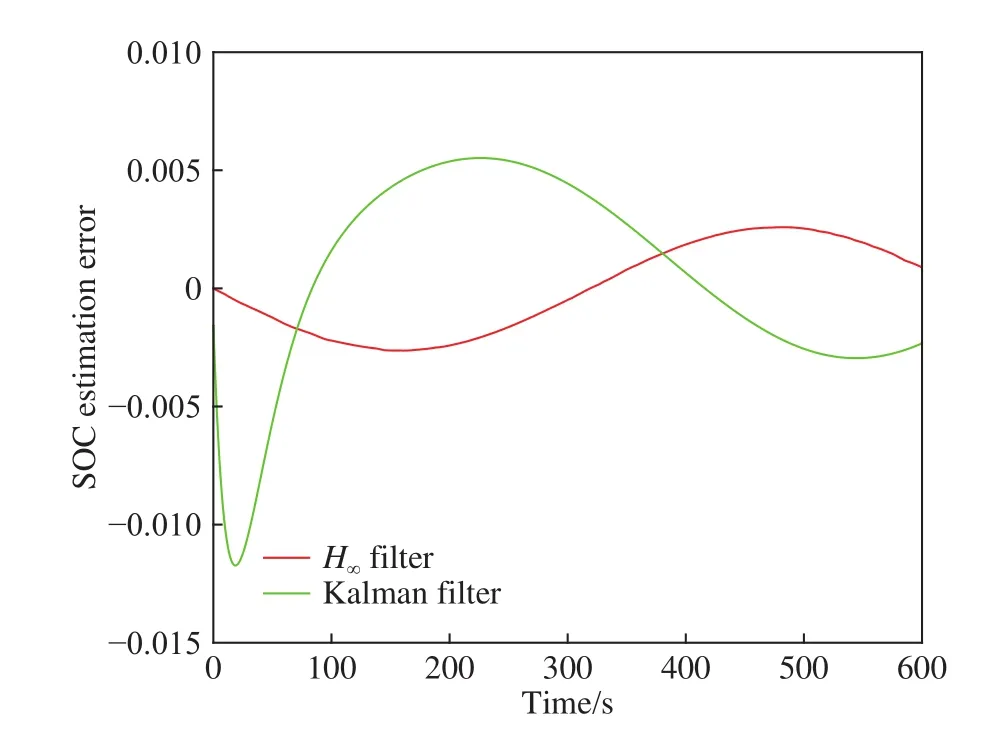
图9 US06激励的 SOC 估计误差Fig.9 SOC estimation error excited by US06

从图4中可以看出，在BJDST动态激励下，基于鲁棒H∞滤波器的SOC估计时间历程曲线比基于kalman滤波的SOC估计时间历程曲线更为接近模型输出值. 图5中BJDST动态激励下的SOC估计误差表明，基于鲁棒H∞滤波器的SOC估计误差波动幅值小于基于kalman滤波的SOC估计误差波动幅值. 从表2中对应的均方根值对比结果可以看出，基于鲁棒H∞滤波器的SOC估计比模型输出大0.1%，而基于kalman滤波的SOC估计相较于模型输出小0.27%. 基于鲁棒H∞滤波器的SOC估计误差均方根值是0.0019，明显小于基于kalman滤波的SOC估计误差均方根值0.0041. 图4，图5以及对应表2中的均方根值分析结果表明，即使在电流信号存在干扰，电池温度持续波动并对模型参数产生一定影响的条件下，所设计的鲁棒H∞滤波器依然能够实现对SOC的准确估计.

表2 SOC 估计及其估计误差的均方根值Table 2 RMS value of SOC estimation and estimation error

四种不同类型动态激励下的SOC估计，以及SOC 估计误差的均方根值（Root mean square，RMS）如下表2所示.

BJDST−FUDS−US06联合动态测试下的SOC估计及其估计误差时间历程曲线如下图10～11所示.

图10 BJDST−FUDS−US06激励的 SOC 估计Fig.10 SOC estimation excited by BJDST−FUDS−US06

图11 BJDST−FUDS−US06 US06激励的 SOC 估计误差Fig.11 SOC estimation error excited by BJDST−FUDS−US06

在FUDS动态激励下，图6中的SOC估计时间历程曲线表明相较于基于kalman滤波的SOC估计，基于鲁棒H∞滤波器的SOC估计与模型输出较为接近. 图7中的SOC估计误差时间历程曲线表明了基于鲁棒H∞滤波器的SOC估计误差波动幅值比基于kalman滤波的SOC估计误差波动幅值要小. 从表2中FUDS动态测试下的均方根值可以看出，基于鲁棒H∞滤波器的SOC估计的均方根值与模型输出的均方根值近乎一致，而基于kalman滤波的SOC估计的均方根值相较于模型输出的均方根值小0.21%. 基于kalman滤波的SOC估计误差均方根值0.0036明显大于基于鲁棒H∞滤波器的SOC估计误差均方根值0.0018. 图6，图7以及表2中相对应的FUDS激励下的均方根值分析对比结果表明，所设计的H∞滤波器不仅具有很好的鲁棒性，而且具有优异的SOC估计性能.

在US06动态激励下，图8中的SOC时间历程曲线和图9中的SOC估计误差时间历程曲线表明，与基于kalman滤波的SOC估计相比，基于鲁棒H∞滤波器的SOC估计更为接近模型输出值.表2中对应的US06动态激励下的均方根值对比结果表明，基于鲁棒H∞滤波器的SOC估计的均方根值与模型输出的均方根值几近一致，而基于kalman滤波的SOC估计的均方根值比模型输出的均方根值小0.1%. 基于鲁棒H∞滤波器的SOC估计误差均方根值是0.0019，明显小于基于kalman滤波的SOC估计误差均方根值0.0043. 仿真实验与均方根值的对比结果表明，所设计的H∞滤波器具有更为优异的SOC估计性能，同时具有很好的干扰抑制效果，即具有很强的鲁棒性.

在BDST−FUDS−US06联合动态测试下，图10中接近10 h的时间历程表明，H∞滤波和kalman滤波的时间历程均比较接近于模型输出结果. 从图11中的SOC估计误差时间历程曲线中可以看出，H∞估计误差比kalman滤波估计误差具有更小的波动幅值. 表2中对应的 BDST−FUDS−US06联合动态激励下的均方根值表明，H∞滤波与模型输出的均方根值均为0.3186，而kalman滤波比模型输出的均方根值小0.35%. 基于kalman滤波的SOC估计误差均方根值0.0033明显大于基于鲁棒H∞滤波器的SOC估计误差均方根值0.0022. 仿真实验与均方根值的对比结果表明，所设计的鲁棒H∞滤波器不仅对外部扰动表现出了很好的鲁棒性，而且能够实现对SOC的强跟踪能力.

5 结论

本文采用LMI技术设计了用于SOC估计的鲁棒H∞滤波器. 该滤波器的设计考虑了锂离子电池模型参数随温度变化产生摄动影响SOC估计准确性的问题. 把电池温度变化对模型参数的影响方式建模为标称电阻值和电池总容量的加性变量，并将电池温度变化看作系统的外部扰动. 通过切线法对模型进行了线性化，并基于该线性化模型设计了估计SOC的观测器. 最后，采用四种不同类型的动态电流激励，并与kalman滤波对SOC的估计结果进行仿真对比，其结果表明所设计的鲁棒H∞滤波器不仅具有优异的SOC估计性能，而且对外部扰动表现出了很好的鲁棒性.