基于融合特征的双通道CNN滚动轴承故障识别

2021-05-19齐爱玲朱亦轩张广明

机械与电子 2021年5期

齐爱玲，李琳，朱亦轩，张广明

(1.西安科技大学计算机科学与技术学院，陕西西安 710054；2.北京化工大学信息科学与技术学院，北京 102200；3.西安科技大学机械工程学院，陕西西安 710054)

0 引言

滚动轴承被广泛应用于工业生产中，它是旋转机械的重要组成部分。确保设备能正常工作的前提是滚动轴承稳定运转，若轴承在长期高负荷条件下持续工作，极易引发故障，从而影响设备性能及稳定性，甚至造成人员伤亡[1]。因此需要对滚动轴承故障展开研究，从而较快识别故障种类，提高设备运行效率，增强设备稳定性[2-5]。

由于机器学习研究的不断深入，应用在轴承故障诊断领域的智能故障诊断算法已成为主流算法[6]。传统的智能故障诊断算法分为特征提取、特征选择和故障识别3个步骤[7]。常用的特征提取方法有频谱分析法(SA)[8]、傅里叶变换(FFT)[9]、小波变换(WT)[4]和经验模态分解(EMD)[10]等。特征选择是对前一步特征提取“去粗取精”，常用的方法有主成分分析法(PCA)[5]和独立分量分析法(ICA)[3]。最后将选择后的特征输入到分类器中，通过对数据的反复迭代输出故障识别的结果[7]。反向传播神经网络(BPNN)、随机森林和支持向量机(SVM)等都被广泛用作故障诊断的分类器，均有良好的分类效果[11-12]。然而此类算法进行特征提取时较依赖本领域内的专家知识和经验，提取过程复杂，算法通用性差，大多只能用于浅层结构提取，不能应用于深层结构中[13]。

近年来，由于深度神经网络有良好的自主学习能力，能够从数据中主动学习到数据的本征特征，给故障诊断领域带来了新思路。一些研究[6，14-17]借助人工提取故障特征，将信号转换为时频图或直接将原始振动信号输入进卷积神经网络并诊断，采集到的振动信号往往混有各种噪声，从而影响信号提取时的时域指标，通常卷积神经网络善于处理二维数据，而一维CNN模型的识别准确率会受到影响。

针对以上问题，为了充分发挥一维CNN模型和二维CNN模型的优势，本文提出一种基于双通道CNN的滚动轴承故障识别方法。

1 基本理论

1.1 Morlet小波

对连续时间m(t)=T2(R)进行连续小波变换，则W定义为

W(α,β)=〈m(t),ψα,β(t)〉=

(1)

母小波通过伸缩平移变换得到ψα,β(t)函数，即

(2)

ψα,β(t)为连续的小波基函数；α为尺度因子，与频率伸缩有关；β为平移因子，与时间移动有关。当α越大时，超声信号的低频特征越容易被提取出来；当α越小时，超声信号的高频特征越容易被提取出来。

连续小波变换要求其小波基函数的波形与故障的信号特征有较高的匹配度，故小波基函数的选择是连续小波变换的核心[18]。滚动轴承故障所产生的故障脉冲特征与Morlet小波波形类似[19]，Morlet小波中的cmor小波表示其复数形式，具有很强的自适应性，故本文将cmor小波作为连续小波的小波基函数。

1.2 卷积神经网络

卷积神经网络CNN 是深度学习中最常用的算法之一，属于多层前馈神经网络[20]。一个典型的CNN包含输入层、隐含层和输出层，隐含层通常由多个卷积层和池化层相交组成，负责对输入数据进行特征提取和降维，输出层通常与全连接层结合组成分类器，Softmax、SVM和逻辑回归等都是分类器[21]。CNN模型如图1所示。

图1 典型的CNN网络模型

1.2.1 卷积层

通常把二维数据作为CNN的输入层数据，在下一层卷积层中，各个卷积核对前一层输入的数据进行加权操作，得到对应的数据特征，利用非线性激活函数将其拼接成为下一层的输入数据，其过程用数学公式表示为

(3)

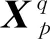
(4)

1.2.2 池化层

卷积层之后一般接入池化层，池化层的主要操作是对上一层提取后的数据进行降维，对特征数据进行简化，从而可以提高数据识别速度。目前最常用的池化方法为最大值池化，可得到输入的局部最大值，有效降低训练数据参数，提高鲁棒性。最大池化公式表示为

(5)

q为特征向量中神经元的数值；l为池化局部区域的宽度；p为神经元对应的数值。

1.2.3 全连接层

全连接层负责将卷积层和池化层处理后的数据进行融合，在Softmax分类器中将融合后的数据进行分类。Softmax的模型表示为

(6)

q为卷积的偏置值；P为权重矩阵；最终输出为W。

1.2.4 双通道的卷积神经网络

双通道的CNN模型采用Lenet-5网络，同时输入二维信号时频图和一维原始信号，使其分别通过各自对应的卷积层和池化层，在汇聚层将各个特征向量进行拼接，最后通过Softmax分类器对轴承故障进行分类。双通道模型如图2所示。输入的二维特征图的大小为64×64，输入的一维原始信号的大小为1×1 024；分别经过各自对应的2层卷积层和池化层，第1层卷积层的卷积核个数为6，第2层卷积层的卷积核个数为16，卷积核大小均为5×5，选用ReLU函数作为激活函数；池化层选用最大池化法，池化层大小为2；全连接层选用Softmax分类器。

图2 双通道卷积神经网格模型

2 实验数据及结果分析

2.1 数据集及准备

本文采用美国斯凯西储大学的轴承数据中心提供的公开数据集，轴承故障采集实验平台如图3所示。该装置由1个1.5 kW电机、译码器、功率测试计和电子控制器组成。本文选用型号为SKF6205，采样频率为18 kHz的驱动端轴承数据，轴承故障种类为内圈故障、外圈故障和滚动体故障，每个故障的损伤直径包括0.07 mm、0.14 mm和0.21 mm，正常轴承数据算一类故障，故共有10种故障状态。

图3 轴承缺陷数据采集平台

本文对驱动端轴承故障的4种不同负载下的故障信号均做了实验，并采用长度为1 024的随机采样方式对轴承数据的振动信号进行随机分割。每种故障类型200个样本，共计2 000个样本。随机选择1 400个样本作为训练集，400个样本作为验证集，200个样本作为测试集。本实验中具体的样本数据集如表1所示。

表1 滚动轴承数据集

滚动轴承在4种不同状态时的信号波形处于内圈故障、外圈故障、滚动体故障和正常状态。仅凭有相关经验的研究人员的直观分辨是能区分出各个信号所对应的状态，但这仅针对个别理想的信号，且非研究人员无法对这些信号做出判断，加上信号间的波形极为相似，凭借肉眼难以区分，仅凭借振动信号的波形图对故障状态进行识别是不可靠的，因此需要将波形图和其对应的时频图相结合进行故障状态识别。

2.2 算法步骤

本文算法有以下几个步骤：

a.首先从CWRU数据集的驱动端轴承数据中读取出故障信号，将信号按照6∶4的比例分为训练集和测试集，设置故障信号的随机采样长度为1 024，给每种故障类型设置标签并采用One-hot标签，以便计算交叉熵时使用。

b.将采样后的数据集进行Morlet小波变换，得到训练集和测试集故障信号对应的时频图。

c.设置时频图大小为64×64，获取前一步得到的时频图和采样后的原始数据，将其使用torch函数转换为单精度格式，设置最佳learning_rate大小为0.005，epoch大小设置为160和200，batch_size大小为24。

d.将时频图输入二维CNN中，卷积核大小为6和16，使用ReLU作为激活函数；将原始信号输入一维CNN中，卷积核大小为6和16，使用ReLU作为激活函数。

e.经过2次卷积层和池化层提取出故障特征，在汇聚层将两特征数据进行融合，用Dropout来防止过拟合现象，大小设为0.5。

f.将拼接后的向量输入Softmax分类器进行训练，不断修改训练参数，选出最佳模型，再对滚动轴承的测试集进行测试。

2.3 时频图的选择

本文分别对故障信号进行小波变换、短时傅里叶变换和广义S变换，其时频图如图4所示。图4所示的时频图，对正常状态下的信号做了时频分析，选用的采样点为1 024，采样频率为48 000 Hz。从图4中可以看出，广义S变换分析出的时频图不能较清晰地显示出信号的特征，短时傅里叶变换则优于S变换，但没有小波变换更清晰，故本文选用小波变换对信号进行视频分析。

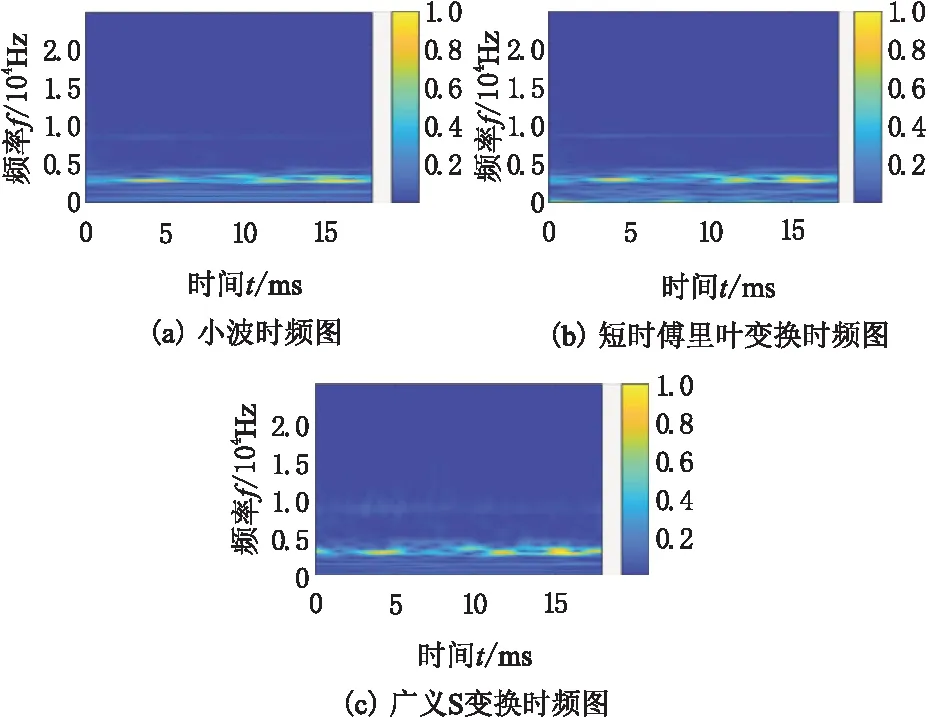
图4 故障信号的3种时频图

2.4 结果分析

实验所用的操作系统为Windows 10，使用的开发工具为Spyder和MATLAB，深度学习框架为PyTorch。使用数据分别为0 hp、1 hp、2 hp、3 hp下的48k的驱动端的轴承数据，将初始数据做小波变换得到对应的时频图，用原始信号和时频图同时作为神经网络的输入，选用1 200个样本为训练样本，800个样本为测试样本，学习率设置为0.005。由于训练大小会对结果产生影响，将每批训练大小分别设置为12、24、32、64。实验表明，当训练大小为24时准确率和速率为最佳结果，对4种不同负载下的轴承数据的比较如表2所示。

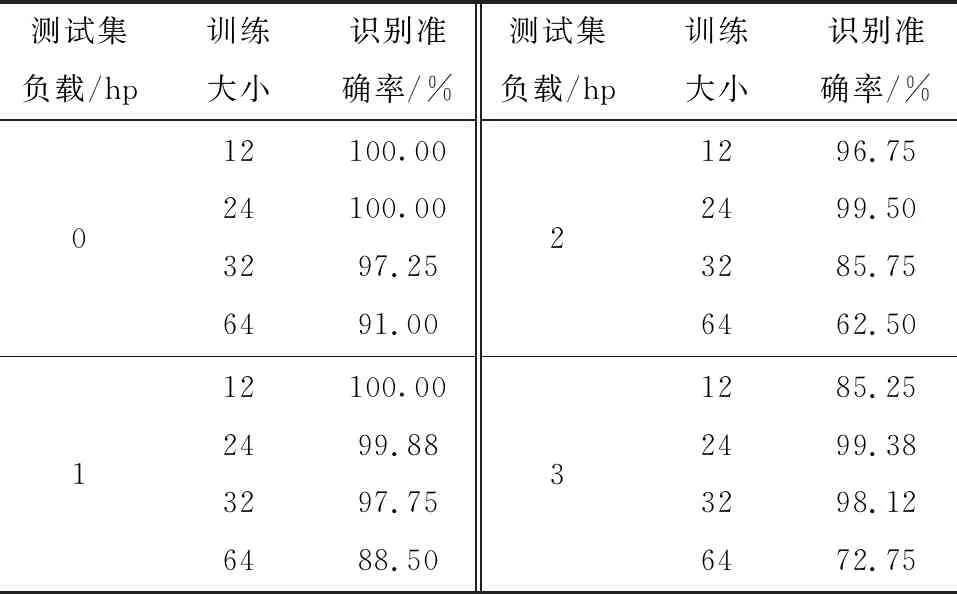
表2 不同训练大小的实验结果

为验证本实验所用方法的有效性，分别对时频图+SVM、时频图+BP神经网络、原始信号+CNN、时频图+CNN、本文原始信号+时频图+CNN方法做对比。相同样本、相同迭代、不同负载条件下，选用训练大小为24时所生成的准确率，本实验所用方法的平均准确率在99.69%。几种方法对轴承故障识别准确率的比较如表3所示。