基于导纳控制算法的电液比例系统联合仿真研究

储亚东，李成刚，陈飞翔，岳云双，王 剑

(南京航空航天大学机电学院，江苏 南京 210016)

0 引言

液压伺服单元因其功率密度大、动作响应快和抗电磁干扰能力强等特点[1]，在机器人领域得到了广泛应用。对于自动化打磨、人机协作等对操作力精度和稳定性要求较高的场合，传统的基于位置伺服的机器人电液比例系统难以满足应用需求，此时需在位置闭环控制的基础上融合环境感知、实时力控等要素，通过内外环结合、实时受力状态补偿的控制方式[2]，对机器人进行柔顺控制，提高机器人电液比例阀控缸驱动单元的鲁棒性和可靠性[3]。

机器人柔顺性可通过增加被动柔顺机构或设计主动柔顺算法来实现[4]。对于主动柔顺控制策略而言，位置伺服是机器人柔顺力控的基础[5]，在电液比例系统的位置控制领域已有大量的研究工作，上海交通大学的何常玉等[6]针对带有负载扰动的电液比例位置系统提出了一种动态面鲁棒控制策略，可实现高精度位置跟踪,且有效避免了传统反步法设计鲁棒控制器时带来的“计算膨胀”问题；天津理工大学的王收军等[7]利用速度反馈和PID控制对电液比例位置控制的动态特性进行了优化，有效提高了系统响应速度和平稳性。在柔顺控制领域，Hogan[8]，Whitney[9]，Salisbury[10]，Kazarooni[11]等人对于阻抗算法的研究工作最具代表性，而Sepehri和Clegg提出的是基于力/位混合控制的电液比例控制器，但由于早期缺乏强大的仿真验证工具，导致控制效果有所欠缺[12]。

本文为满足某工程液压机器人的作业需求，提出了一种基于导纳控制算法的电液比例柔顺控制器，搭建了一种强大的、全新的机电一体化联合仿真平台，并对研究对象的控制性能进行了多算法、跨平台的联合对比仿真分析，验证了柔顺控制器的适用性和可靠性。

1 系统组成和原理描述

电液比例控制系统按照液压动力元件的控制原理，可分为节流控制式(阀控式)和容积控制式(变量泵、变量马达控制式)2大类[13]。其中，节流控制式又以阀控缸这种典型系统为代表，通常搭配位移传感器组成闭环控制。一个典型的基于位置闭环的电液比例系统组成原理如图1所示。

图1 电液比例阀控缸位置闭环原理

考虑到液压机器人的实际控制要求，本文以电液比例阀控缸系统为研究对象，设计了专用的基于PID位置内环的导纳控制器，并分别进行了系统在弹簧阻尼和刚性碰撞环境下的联合仿真分析。其中，设计的碰撞实验平台结构组成如图2所示。系统主要由对称式电磁比例阀、平台底板、非对称液压油缸、拉杆式位移传感器、直线导轨模组、位置挡板、工作顶板、油管和支架等附件组成。

图2 电液比例阀控缸实验平台结构

常规的位置伺服控制原理为：泵站经由电磁比例阀给液压缸供油，驱动活塞杆按照一定的规律运动，具体的负载位移量由固定在油缸上的拉杆式位移传感器负责监测与反馈，在控制器中将返回的实际位移值与期望位移信号相比较，偏差量通过比例放大器放大并转换成控制电流信号，驱动电液比例阀中的比例电磁铁，将信号电流的大小和正负成比例、连续地转换成机械量推动阀芯运动，进而改变比例阀开口状态，使得流入液压缸两腔内的流量发生变化，推动活塞杆运动，实现负载实际位移对期望输出信号的快速、准确跟踪[14]。

在上述驱动器位置伺服控制的基础上，本文对电液比例系统的控制器加入了基于导纳算法的外部作用力闭环，通过活塞杆末端的力传感器将系统与环境的作用力实时反馈给控制器，根据导纳算法将作用力的实际值与控制策略所设计的期望阈值进行比较，根据偏差值对油缸位移进行及时修正，进而实现电液比例系统的柔顺控制。

2 比例阀控非对称缸数学模型

在软件仿真之前，可先求解电液比例系统的动态数学模型，用作验证和参考。机器人液压系统各元件参数已根据实际工况和控制要求进行了初步确定，其中油缸行程L=320 mm，缸径D=40 mm，活塞杆直径d=22 mm，据此可求解此液压油缸的实际工作面积为8.77 cm2，比例阀与油缸之间管道长度约为L管=1.5 m，油管外径D管=15 mm，壁厚Δd=4 mm，液压系统总压缩容积为511.39 cm3。

电液比例位置系统的动态分析一般处于零位的工作条件之下[15]，这里认为增量和变量相等，故比例阀的线性化流量方程为

qL=KqXV-KopL

(1)

液压驱动器件的流量连续性方程为

(2)

Ctp为油缸的总泄漏系数，而等式右侧分别为系统总泄漏流量、推动油缸运动所需流量和系统总压缩流量。

非对称液压油缸负载力与输出力的平衡方程为

(3)

mt为油缸活塞杆和负载总质量；BP为油缸活塞杆及负载的粘性阻尼系数；FL为作用在活塞杆末端的外部负载力；K为负载弹簧刚度。

电液阀控缸的动态特性由式(1)、式(2)和式(3)决定，对其分别做拉氏变换，联立之后消去中间变量，并依据惯性负载特性简化，得到油缸活塞杆的总输出位移为

(4)

Kce为系统压力-流量系数；XV为比例阀阀芯位移。

当指令输入为XV，油缸-负载的传递函数为

(5)

系统的流量-压力系数Kce=Kc+Ctp，其中油缸的总泄漏系数Ctp一般要比阀的流量-压力系数Kc小得多[15]，故Xh主要是由参数Kc来决定的。系统的零位压力系数为

(6)

W为比例阀的面积梯度；rc为比例阀的阀芯和阀套之间的间隙；μ为油液的动粘度。

对于全开口的电液比例阀W=πd阀，取d值为7.9 mm，阀的面积梯度W=24.8 mm，可求得零位压力系数Kco=43.47×10-13m·/(N·s)，由经验取ξh=0.2。可依据下式求非对称液压油缸的数学模型：

(7)

电液比例阀的传递函数结构形式为

(8)

根据华德4WREE伺服比例阀手册中的频响特性曲线，可求得KSV，则电液比例阀的传递函数为

(9)

最后，将电液比例阀控缸系统表示为如图3所示的动态模型。

图3 电液比例控制系统动态数学模型

3 基于PID位置伺服的导纳控制器设计

阻抗控制属于机器人主动柔顺控制策略中的一种，从严格意义上又可分为基于力的阻抗控制和基于位置的导纳控制[16]。本文重点研究的是导纳控制，其本质属于力控制，但实际上并不是直接对机器人作用力进行控制，而是通过执行器的位置或速度与作用力之间的相互关系来进行控制的[17]，最终实现对机器人作用力的主动柔顺控制。

本文基于对称比例阀控非对称缸单元，运用导纳算法实现了执行器的主动柔顺力控制，设计的导纳控制器结构如图4所示。

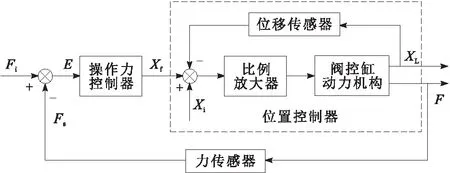
图4 基于位置和操作力伺服的导纳控制器结构

工作原理为：系统采用内外环控制结合的方式，其中内环为基于PID的位置伺服，外环为基于导纳的力伺服，系统执行机构精确、快速的位置伺服控制通过PID内环来实现，在位置跟踪的基础上应用导纳算法对位置控制器的期望输出信号进行实时补偿，根据系统与环境的接触力来修正执行器的实际位移量，使其及时停止进而避免更为剧烈的刚性撞击，实现柔顺控制效果。

导纳控制补偿器结构如图5所示，其控制率可用式(10)来表达。

图5 导纳控制补偿器结构

(10)

导纳控制是一种力闭环控制，需在机器人的执行器与负载间布置一个力传感器用于对操作力的实时反馈，之后将实际值与工况允许值或者计算得到的理想阈值进行比较，根据力的偏差量来对内环的位置控制器进行补偿，调整期望的位移输出量，进而实现活塞杆实际位移量的及时修正。

4 联合仿真分析

本文借助于工程领域常用的MATLAB/Simulink、AMESim和Simcenter 3D仿真软件，对设计的电液比例系统导纳控制器在不同工况环境下进行了仿真分析。首先，搭建Simulink-Amesim联合仿真平台，通过接口将Simulink中的导纳控制程序与AMESim的电液比例阀控缸系统在弹簧阻尼环境下进行了联合仿真分析，并与传统PID位置伺服控制器进行了性能对比，验证了导纳算法在电液比例控制系统的柔顺性控制中所起到的作用，为液压机器人的多关节同步柔性控制积累了经验。其次，在上述联仿平台的基础上，又加入了Simcenter 3D动力学仿真软件，搭建了基于Simulink-AMESim-Simcenter 3D的三软件联合仿真平台，其原理如图6所示，对系统的控制、液压、动力学进行了更为全面、准确的仿真分析，验证了基于PID位置伺服的力导纳控制器在实际碰撞工况下的柔顺性表现，实现了预期效果。

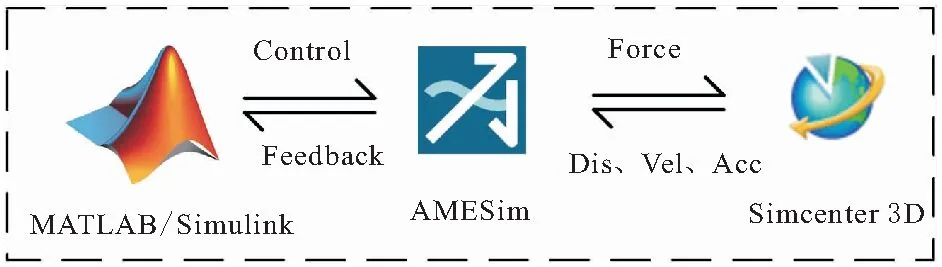
图6 Simulink-AMESim-Simcenter 3D联仿原理

4.1 基于Simulink-AMESim的弹簧阻尼系统仿真

本文对设计的导纳控制器进行了基于Simulink-AMESim的联合仿真分析。首先在AMESim的草图模式下搭建了电液比例系统原理图，选择合适的元件子模型类型，对表1中的仿真参数进行了设置，编译成功之后会生成mex64格式的联合仿真文件。

系统由电机、定量泵、溢流阀、蓄能器、伺服比例阀、压力传感器、非对称液压缸、弹簧阻尼系统和力传感器等元部件组成。接口模块的主要功能是实现AMESim和Simulink软件仿真数据的互通，将位移、速度和加速度等运动量传送给Simulink软件，待控制器处理完成之后，将控制信号通过接口文件再回传给AMESim液压系统，实现联合闭环控制仿真。

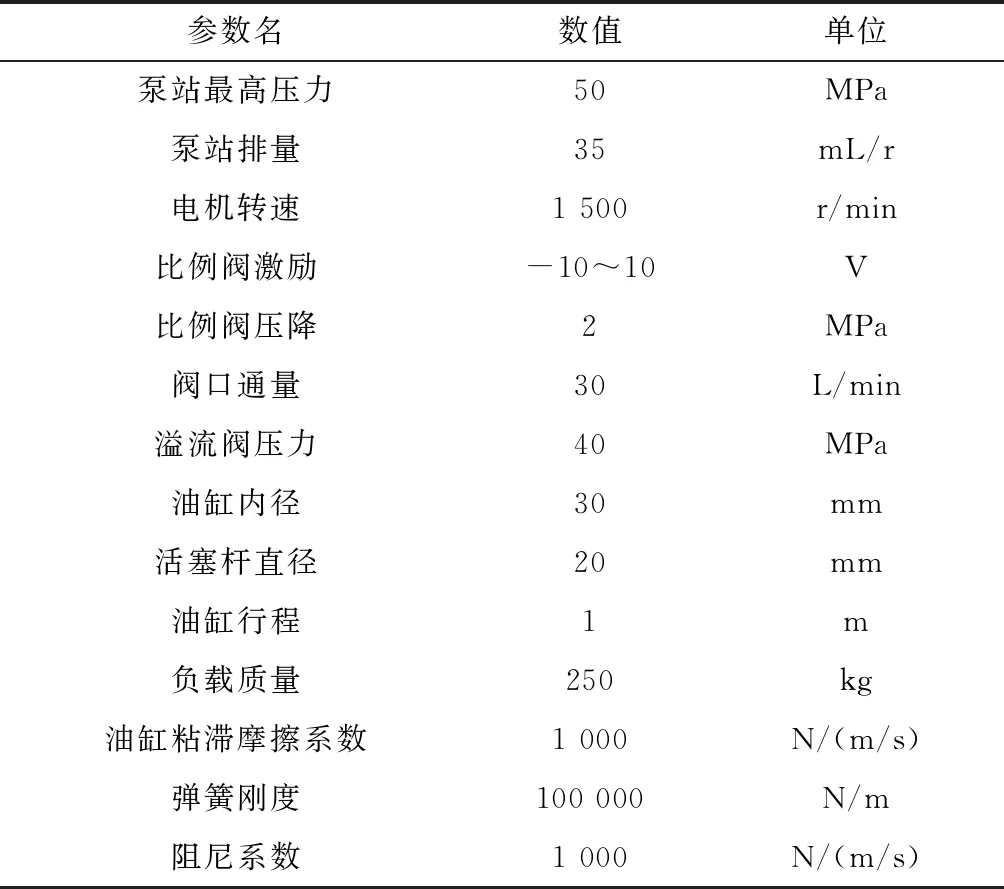
表1 液压模型仿真参数

本文设计的导纳控制器主要分为2个控制闭环，内环为基于PID算法的位置伺服，外环为系统与环境的接触力闭环。通过Manual Switch模块来决定是否引入导纳控制算法，进而实现纯位置控制和导纳柔顺控制的切换。

经过对控制器参数的仿真优化，在满足位置伺服精度和快速性的基础上，电液比例系统的稳定性和鲁棒性均达到了预期的设计目标，超调和振荡较小，执行器运动迅速而平滑。在图7和图8中，将纯位置控制和导纳控制的位移和接触力曲线进行了整理，方便对仿真结果的对比分析。

通过程序中的Switch开关模块，先将系统切换至纯位置控制模式。本文采用基于PID算法的位置控制策略，给定的期望位移值为0.20 m，其实际位移与操作力的仿真结果如图7和图8中虚线所示。从仿真结果可以发现，在PID位置伺服模式下，油缸位移可以较快地速度平稳地达到期望的0.20 m，此时油缸活塞杆与环境的作用力最终稳定在20 kN左右。

双击Switch开关将程序切换至导纳控制模式，此时PID控制器仅作为位置伺服内环，期望的位移量依然设置为0.20 m。不同的是，控制器多了一个接触力伺服闭环，用于根据油缸与环境作用力实现对位移量的修正，此时设置的作用力阈值为15 kN，仿真结果分别如图7和图8中的实线所示。从结果能看出，由于导纳控制器的介入，此时油缸与弹簧阻尼系统的实际接触力已从原先的20 kN调整为15 kN，且响应速度略有提升，实现了良好的力柔顺控制。与此同时，由于导纳控制器对于PID位置控制器的补偿，此时活塞杆不会一直移动到位置闭环所期望的0.20 m，实际位移量大约为0.15 m左右，与弹簧胡克定律是相符的，即弹簧的作用力与位移量呈线性关系，进一步验证了导纳控制算法的正确性。

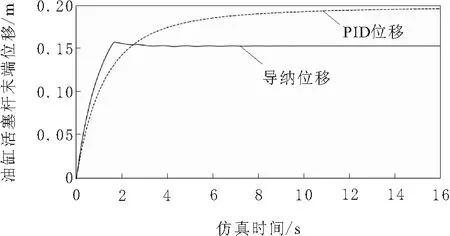
图7 位置伺服与导纳柔顺力控的位移曲线

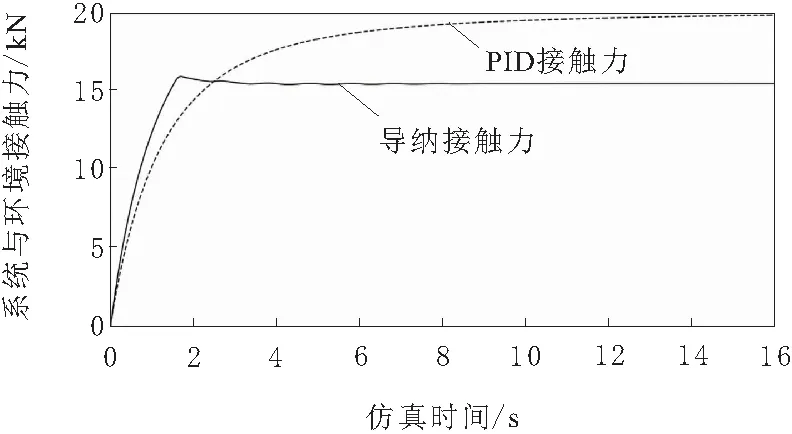
图8 位置伺服与导纳柔顺力控的接触力曲线

4.2 基于Simulink-AMESim-Simcenter 3D碰撞仿真

为分析导纳控制器在实际碰撞情况下的柔顺性能，本文通过Simcenter 3D软件建立了如图9所示的用于实现碰撞效果的电液比例阀控缸动力学仿真模型，顶针和障碍物的初始间隔为0.20 m，碰撞参数整理如表2所示。将Simcenter 3D软件与4.1节搭建的Simulink-AMESim仿真平台进行结合，实现真正的机电液一体化联合仿真研究，对控制算法的性能进行更为可靠的验证和优化。

图9 电液比例阀控缸Simcenter 3D动力学模型

本文将AMESim中的仿真位移和接触力曲线进行导出并分析，可得PID位置伺服和导纳柔顺力控模式下，位移与接触力曲线分别如图10和图11所示。

表2 碰撞仿真参数

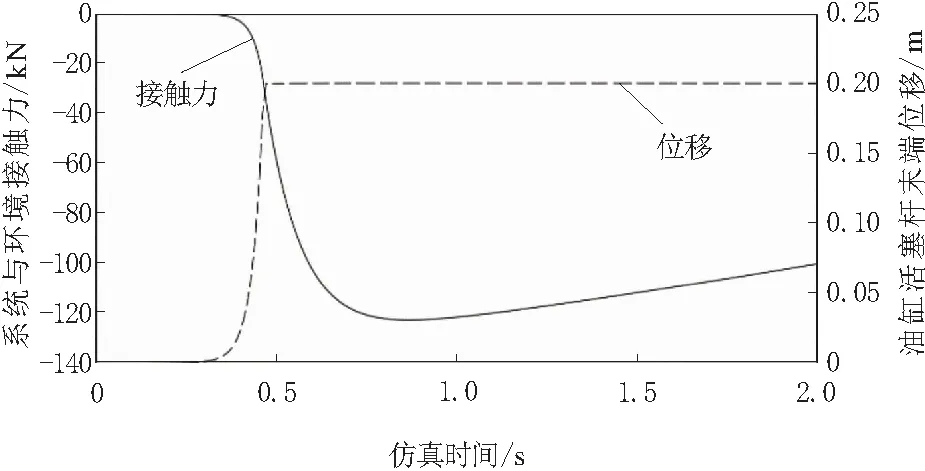
图10 PID位置伺服的位移与接触力曲线

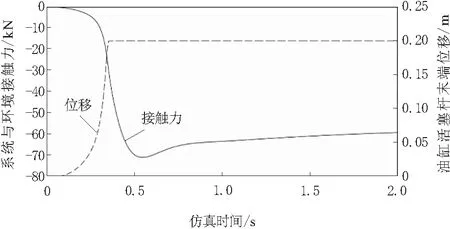
图11 导纳算法补偿后的位移与接触力曲线

为了更好地研究碰撞之后的接触力变化规律，PID位置控制器的期望位移必须大于Simcenter 3D物理模型中的碰撞距离，此处设置为0.40 m。由图10的仿真曲线可看出，由于动力学模型中障碍物的存在，在纯位置伺服控制下油缸活塞杆的实际位移只能达到0.20 m，碰撞大约发生于0.5 s，在接下来的0.5 s时间内，由于位置控制器依然迫使油缸朝着期望位移量运动，所以比例阀的阀口依然处于打开状态，油腔压力不断增加，导致活塞杆与障碍物的挤压力也一直增加，直到液压系统的最高压力达到溢流阀的设定值之后，碰撞力才最终达到120 kN的峰值。

通过Switch开关引入导纳控制算法，将接触力阈值设置为60 kN。根据图11的仿真结果来看，活塞杆在0.35 s的时刻运行到了0.20 m，并与障碍物发生了接触，之后的作用力会短暂增加到70 kN并开始降低，最终在2 s的时候能稳定到60 kN的期望值，此时的碰撞力峰值为70 kN，相比于纯位置伺服状态下的120 kN，此时的碰撞程度大大减轻，体现出了良好的柔顺性，说明设计的导纳算法可较好地满足电液比例阀控缸系统的柔顺控制要求。

通过以上仿真分析，本文设计的基于导纳算法的力控制外环，可根据实际与环境作用力对位置内环中期望的位移量进行补偿修正，通过动态调整比例阀的阀芯位置，使阀口开度及时减小或关闭，关停液压缸使其油腔压力不再增加，也就实现了碰撞力的柔顺可控，达到了期望的电液比例柔顺控制设计要求，且具备较好的鲁棒性和可靠性，对于液压机器人的多缸同步联动过程的柔顺控制具备一定的参考价值。

5 结束语

本文考虑多自由度串联液压机器人的柔顺化控制需求，对电液比例阀控缸系统提出了一种基于位置伺服的导纳柔顺控制器，建立了电液比例系统的动态数学模型，利用MATLAB/Simulink、AMESim和Simcenter 3D软件各自的优势搭建了联合仿真平台，对导纳控制器在一般弹簧阻尼环境和刚性碰撞情况下的柔顺性能进行了仿真验证和优化分析，取得了较满意的效果，初步实现了预期的研究目标。

但现有的研究方法在内外环控制器的参数平衡优化上还有待提高，目前存在的问题是位置伺服的响应时间过长，控制器的内外环参数需同时调校，若一味地增加PID位置伺服内环的响应快速性，则会使导纳算法补偿之后的位置控制信号出现超调或振荡；若仅为保证系统柔顺控制的稳定性，那么系统位置伺服的响应速度又受到了影响。问题的关键点在于寻求控制器内外环参数优化的最佳平衡点，使得系统的位置跟随能达到最快响应速度，此时又能保证单位置闭环或者导纳柔顺控制不会出现超调或振荡，实现快速性和稳定性的最佳平衡，使得电液比例阀控缸系统的控制性能达到最优化，这是后续的研究工作所需要完成的内容。在“单阀-单缸”系统的基础上可对三自由度液压机械手多缸联动过程的柔顺性进行研究，满足部分对力控要求较高的工业液压机器人的性能要求，这也体现了当前柔顺技术在液压控制领域的应用空间较大，具备良好的发展前景。