一类分数阶微分方程在集合Ph,e上解的存在唯一性
2021-05-19刘宏伟
刘宏伟
(太原学院 数学系,山西 太原 030001)
0 引言
由于分数阶微积分具有记忆性质(非局部性),它非常适合于刻画具有记忆和遗传性质的过程。近年来,越来越多的理论和实验表明,应用科学和工程中出现的许多现象都可以通过分数阶微分方程来描述,并凸显了其独特优势和不可代替性。这类问题的数学模型最终可归结为分数阶微分方程的定解问题,特别是解的存在唯一性、多重性、稳定性及爆破解问题,其理论和应用研究在国际上已成为一个热点[1-11]。这些结果主要用锥理论、Guo-Krasnosel’skii不动点定理等方法研究了解的唯一性、存在性与非线性边值条件下正解的多重性。
文献[12]研究了以下分数阶三点边值问题

利用Guo-Krasnosel’skii不动点定理,得到了方程正解的存在性,其中算子需满足全连续性。
文献[13]研究了如下非线性分数阶三点边值问题
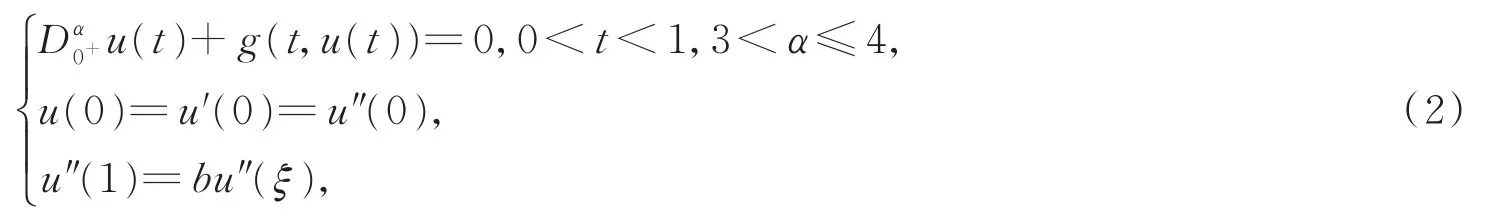
利用半序集合上的不动点定理,得到了方程正解的存在唯一性结论。
文献[14]研究了如下任意阶非线性微分方程
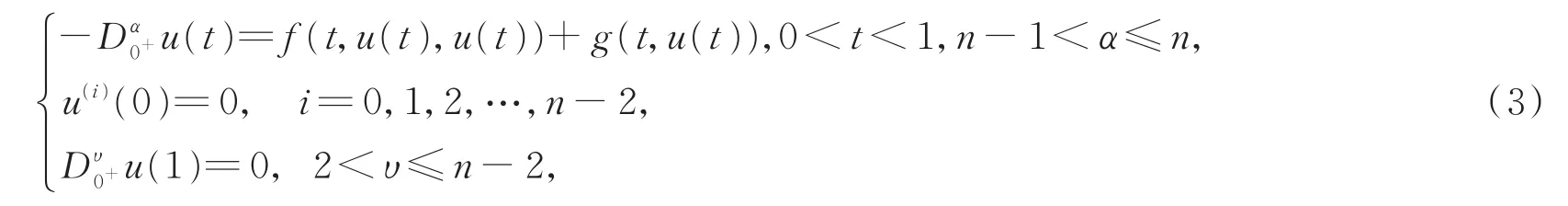
利用混合单调算子的不动点定理,得到了方程正解的存在唯一性结论。
受到上述文献的启发,问题(1)不能解决函数满足混合单调性的情况,问题(2)对于高阶的分数阶微分方程以及含有非线性项的情况都无法解决,为此本文研究以下非线性分数阶微分方程
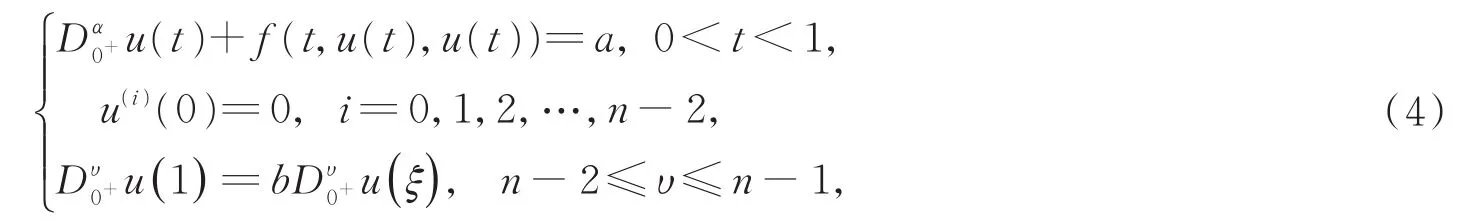
其中n-1<α≤n,n-2<υ≤n-1,0≤b≤1,0<ξ<1,α-υ-1≥0,a>0 为常数,表示α阶的Riemann-Liouville分数阶导数。利用锥理论和定义在集合Ph,e上混合单调算子的不动点定理,获得了问题(4)的非平凡解的存在性和唯一性,并构造了迭代序列来逼近该唯一解,最后给出具体实例验证结论的正确性。
相较于已有文献,本文作出如下推广与改进:
1)给出了一个新的凹算子不动点定理;
2)当n=2,a=0,且f(t,u(t),u(t))=f(t,u(t))时,方程(4)退化为方程(1);当n=4,υ=2,且g(t,u(t))=0时,方程(4)为方程(2)的推广;
3)本文研究的非线性项f(t,u(t),u(t))具有混合单调性,而且方程中常数a>0,此时利用集合Ph上的混合单调算子不动点定理无法解决该问题;而本文应用集合Ph,e上混合单调算子不动点定理获得了a>0时的解存在唯一性结论,推广和改进了已有文献中相关结论。
1 预备知识
定义1[8]称P是正规锥,若存在常数N>0,使得:对x,y∈E,θ≤x≤y,有‖x‖≤N‖y‖。
定义2[8]对于x,y∈E,符号x~y表示存在λ>0和μ>0使得λx≤y≤μx。显然,“~”是一个等价关系。对于h>θ(即h≥θ且h≠θ),定义集合Ph={x∈E|x~h}。显然Ph⊂P。
定义3[9]取h>θ(即h≥θ且h≠θ),取e∈P,且θ≤e≤h,定义集合Ph,e={x∈E|x+e∈Ph},即:
Ph,e={x∈E|∃μ=μ(h,e,x)> 0,ν=ν(h,e,x)> 0,使得μh≤x+e≤νh}。
引理1[15]若x∈Ph,e,那么当λ> 0时,λx+(λ-1)e∈Ph,e。
引理2[15]若x,y∈Ph,e,则存在r∈(0,1)使得:

引理3[10]令n-1<α≤n,n-2≤υ≤n-1,t∈[0,1],那么以下边值问题
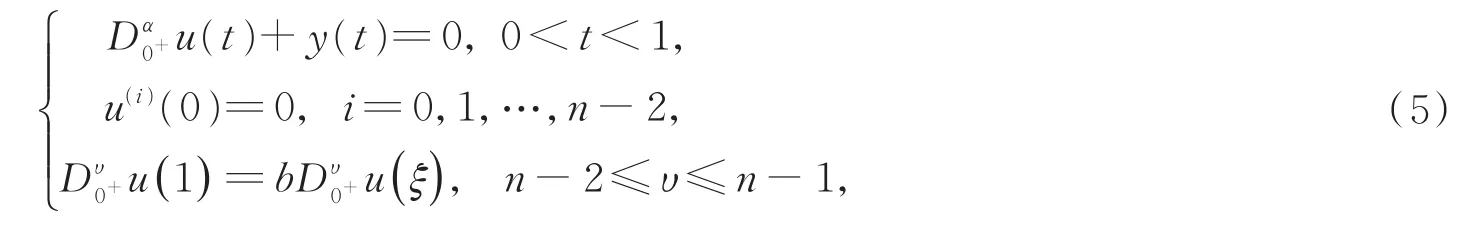
有唯一解u∈C1[0,1],
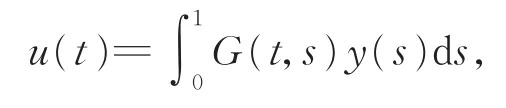
其中
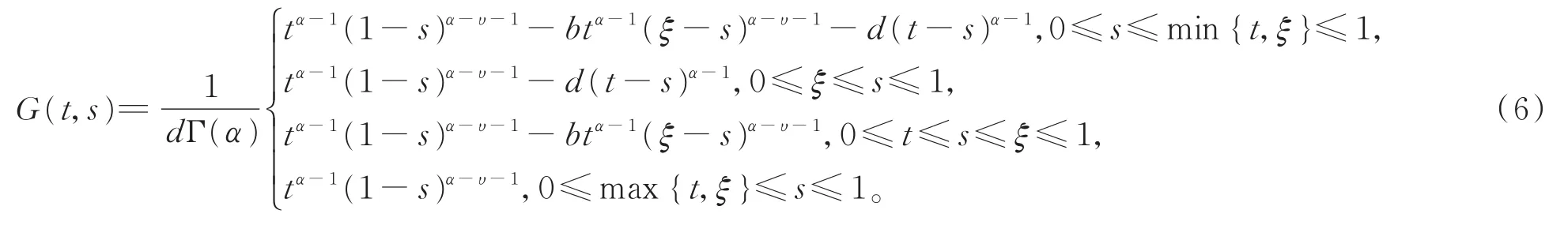
引理 4[10]格林函数G(t,s)有如下性质:
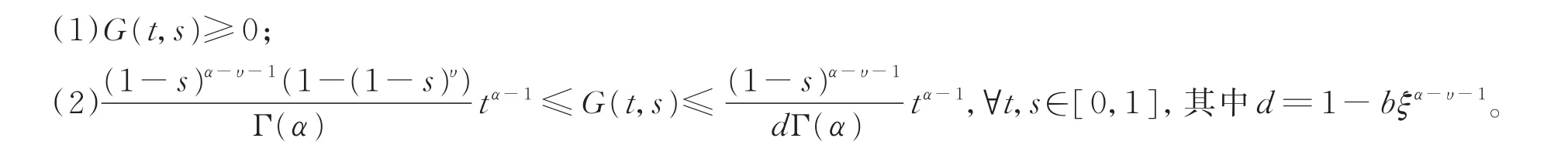
2 主要结论



3 应用





