基于点互信息语义相似性的向量空间模型
2021-05-19牛奉高赵霞徐倩丽
牛奉高,赵霞,徐倩丽
(山西大学 数学科学学院,山西 太原 030006)
0 引言
大数据时代,文本数据极大丰富的同时,资源检索精度下降,检索成本也在增加,我们往往渴望快速获得自己理想的资源,因而,对信息检索、文本分类与聚类、自动问答系统等的要求也进一步提高。语义相似度计算则是这些应用的必要技术[1]。词语相似度用于度量两个词语之间是否存在语义关系,以及语义关系的强弱,是自然语言处理(Natural Language Processing,NLP)的关键环节,也是信息检索、问答系统、情感分析等众多NLP下游应用的基础,所以如何正确计算词语的相似性显得尤为重要[2]。在文本分类和聚类领域,语义相似度的计算起着重要的作用,只有充分、准确的提取挖掘文本中词与词之间的语义信息,才能使词之间相似度的计算更加精准,进而更好地对文本进行分类、聚类,在应用中达到理想的效果。本文主要利用点互信息(Point Mutual Information,PMI)估计特征词间的语义相似度,结合共现潜在语义向量空间模型(Co-occurrence Latent Semantic Vector Space Model,CLSVSM)思想,构建新的文本表示模型,提高信息检索精度,降低检索成本。同时将点互信息估计特征词间语义相似度的方法与word2vec[3]估计语义相似度的方法进行比较,突出前者的优势所在。
1 研究现状
1.1 相关研究现状
文本的表示源于信息检索研究。文本表示是文本分析工作中最基础的一个环节,文本表示的结果会直接影响文本分析的效率和准确率[4]。最基本的表示方法是由Salton[5]提出的向量空间模型(Vector Space Model,VSM),它将每个文献映射为词空间中的高维向量,因此在进行文本聚类时,文本之间语义的相似度计算便转化为向量空间中向量距离或夹角的计算,即:通过相应向量的聚类实现文本聚类[6]。然而,VSM对词间语义关系的忽视,造成了词语独立存在、词向量呈现正交关系的现状,因此,文本聚类精度不高。基于此,Wong等[7]提出广义向量空间模型(Generalized Vector Space Model,GVSM),该模型表示非正交空间中的文献,挖掘了词之间的部分共现信息,但是仍未充分提取。进而,牛奉高[8-9]针对语义信息提取不充分的问题,提出了CLSVSM,并且对共现分布进行了讨论。该模型通过提取特征词之间潜在共现信息来实现对布尔模型的补充,最终构建的CLSVSM相比于VSM有更好的聚类效果。该方法说明在表示模型中深度挖掘语义信息对文本主题聚类有着巨大的意义。
语义信息是否被充分的提取,将直接影响文本聚类精度的高低,而语义信息的提取依赖于语义相似度的计算,因此,必须对词语间的相似度进行精确的计算。自然语言处理中,一般用基于语料库的算法和基于语义资源的算法来进行词语语义相似度的计算。基于语义资源计算词语间的相似度是通过计算词语在语义词典概念层次体系中的距离、深度等来实现的。其中,刘群等[10]语义相似度算法的提出运用了《知网》的层次体系,该方法将词语间相似度的计算转化为义原间相似度的计算。义原为表达词语的最小单位,因而提高了语义相似度计算的准确性。此后,李素建等[11]在计算语义相似度时结合运用了《知网》和《同义词词林》两个语义词典,充分融合二者的词典体系,拓宽了语义相似性计算方法的使用范围;王斌等[12]通过计算层次树中两个节点之间的路径长度来计算词之间的相似性,该方法忽略了节点间的密度信息,导致词间相似性计算不准确;对此,吕立辉等[13]在计算相似度时综合运用词语的密度和路径信息,使计算出的相似度更加符合实际。基于语料库的算法是通过对词与词之间的信息量、共现频次等进行统计来计算相似度的。例如,Lee等[14]采用相关熵来计算词之间的语义相似性,并衡量相似性关系的强弱;Dagan等[15]提出基于分布相似性的概率词关联模型,该模型将语义相似度的计算转化为词语间距离的计算,解决了词语间相似性计算繁琐的问题;随后,Pantel[16]利用点互信息,将词间点互信息作为余弦夹角各维的权重来计算词之间的相似性,进一步提取了词间潜在语义相似性。由上可见,点互信息对词语语义相似性的可行性和有效性。
1.2 CLSVSM回顾
CLSVSM是牛奉高等人[8-9]针对VSM的不足,利用特征词间共现信息,提取挖掘特征词与文献间的潜在语义信息,再对原始布尔模型进行补充得到的高维向量表示模型。该模型的提出,相较于传统的VSM和GVSM,挖掘了更多的潜在语义信息,不仅提高了文本聚类的精度,而且在一定程度上降低了高维向量稀疏的问题。共现分析是对事物共现现象的研究,所谓共现是指文本特征项,如:作者、题名,关键词等共同发生的情况。在我们的研究中特征项指关键词。关键词高度概括文章的内容[17],同时也是文献标引工作中用来标示文献主要内容信息的词汇或术语,因此本文选择关键词来表述文献。在CLSVSM的构建过程中,首先通过统计文献关键词词频得到篇-词矩阵A,然后得到一系列矩阵:共现矩阵C、共现强度矩阵B,以及对布尔模型进行补充后的新篇-词矩阵。补充过程即为CLSVSM的构建过程。构建模型时引入新的指标集,表示文献i所包含的特征词在此空间中的序号集合,如式(1)所示(本文改变了其记号):
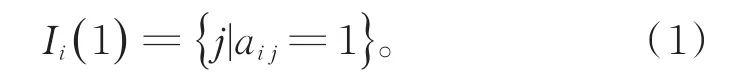
当aij=0时,用来量化关键词j与文献i的语义关系,进而实现对布尔模型的补充得到CLSVSM,其表达式如式(2)等所示:

其中bjt为共现强度矩阵B中的元素,表示第j个关键词与第t个关键词间的共现强度关系。式中di为第i篇文献,aij为第j个关键词在第i篇文献中的权重值。qij的表达式中:当qij=1时,表示关键词j出现在第i篇文献中,当qij=0时,表示文献i中没有找到关键词j,且该关键词与其他关键词不存在语义上的关系,即在该文献中不含有与关键词j的共现关系。
最后用CLSVSM中的各值构建新的篇-词矩阵Q,用于文本主题聚类。
2 基于点互信息的语义相似度计算
2.1 基于点互信息的语义相似度研究
互信息(Mutual Information,MI)[18-19]来源于信息论,是对词语间相似性的一种度量[20]。在自然语言处理中,许多学者应用传统的互信息方法来进行语义相似度的计算[21]。 Pantel[16]首次提出利用点互信息来计算词语间相似性,并提出一种新的聚类方法 CBC(Clustering By Committee)。马海昌等[20]在同义词抽取的研究中,利用互信息和潜在语义相结合的方法度量词语间的相似性,解决了同义词抽取中语义相似度计算不精确的难题。
2.2 基于点互信息的语义相似度计算
自然语言处理中,很多方法可以度量语义相似性,互信息为其中之一。互信息多用来度量随机变量间相互依赖的程度[22-24]。假设给定两个离散型随机变量X和Y,并分别设置它们的样本空间S和T,二者的联合分布p(x,y),以及各自的边缘分布p(x),p(y),则二者间互信息的计算方法如式(5)所示:
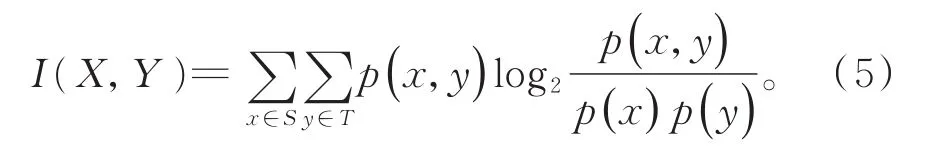
从上式可以看出,当两个随机变量相互独立时,其互信息为0,意味着两个变量间不存在相互重叠的信息。总之,随机变量间的互信息与其之间的相关性成正比关系[25]。
当随机变量为连续型时,互信息的计算方法如式(6)[26]所示:
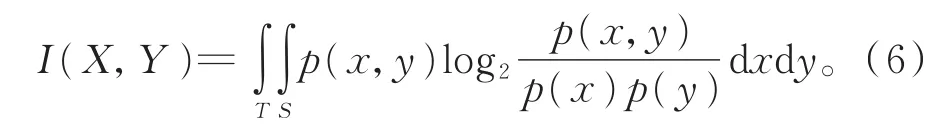
本文采用互信息的衍生概念——点互信息,通过两个关键词在文献中的共现频次来计算相似性。文中统计所收集文献中任意两个关键词之间共同出现的频次,计算二者之间的点互信息,来衡量关键词间的相似性。设有关键词x和y,则两关键词间点互信息的计算方法如式(7)所示:
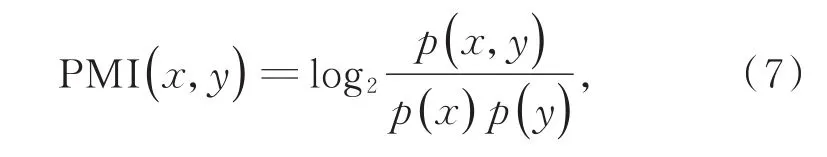
式中p(x,y)表示关键词x和y共现的概率,p(x),p(y)分别表示关键词x和y各自出现的概率。
本文综合考虑其实际意义。例如当两个关键词间的共现频次为0时,二者间PMI的值为-inf,表示两个词间存在微弱的相反关系,但实际意义表示这两个词没有共现,因而此时作者将该PMI值赋为0。
下面将对关键词间相似度的计算步骤进行详细的阐述:
(1)根据收集到的文献数据,(经过简单的预处理,以本文使用的第一个中文数据集为例,即去除不含有关键词的文献)提取文献所含关键词;
(2)统计关键词词频,并按降序排列;
(3)由词频统计表生成文献-关键词矩阵A=(aij)n×m,简称篇-词矩阵,用来表现关键词在文献中的出现情况,即元素ai j=1表示关键词j在文献i中出现,ai j=0表示关键词不出现,其中共有n篇文献,m个关键词。篇-词矩阵中的元素非0即1,为布尔权重;
(4)由篇-词矩阵生成关键词-关键词共现矩阵C=ATA,简称共现矩阵,用来表示两个关键词间的共现情况。矩阵中各个元素cij为所对应的两个关键词i,j共现的频次;
(5)由点互信息的定义式和共现矩阵中关键词间的共现频次数据来计算任意两个关键词间的点互信息。计算方法如式(7);
(6)计算出关键词间点互信息之后,我们在挖掘两个关键词间语义相似度时需要构建一个与这两个关键词同时共现的关键词共现向量V;
(7)关键词共现向量构建完成后,利用余弦夹角公式,计算两个关键词间潜在语义相似度Rel(x,y),如式(8)所示:
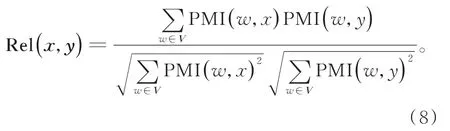
其中向量V为上述构建的关键词共现向量,w为其中的元素,即与关键词x和y同时共现的关键词。Pantel[16]在提出利用点互信息,将词间点互信息作为余弦夹角各维权重来计算相似度的方法中,并没有明确表示向量V的含义。本文在此基础上对向量V作出解释,即上述提出的关键词共现向量。
(8)式使原本没有共现关系的两个关键词,通过构建关键词共现向量,进一步提取挖掘了关键词间的潜在语义相似关系,使语义提取更加充分,关键词共现向量在这里起到了桥梁的作用。
3 语义增强的CLSVSM
文献主题聚类中,不仅需要充分提取挖掘关键词间的语义相似信息,还要将文献与关键词间的语义关系考虑在内。文献与关键词的语义相似性主要用于衡量该文献与其不包括的关键词之间的主题接近性,并将其作为文献在词空间中该维度上的坐标分量,与文献中所含的关键词共同表征该文献的语义信息[27]。CLSVSM在VSM的基础上进行共现分析挖掘潜在语义。本文基于CLSVSM,利用点互信息提取、挖掘关键词间潜在语义相似关系,提出基于点互信息的CLSVSM,并通过提取出的潜在语义相似关系修正布尔模型中关键词在相应文献中的权重,提出语义增强的CLSVSM。
3.1 基于点互信息的CLSVSM
CLSVSM利用关键词间最大共现强度来对传统VSM中权重为0位置的潜在语义进行估计。虽然该模型降低了VSM的稀疏性,提高了文献聚类的精度,但该模型主要度量了文献与词之间的潜在相似性,如果再加上关键词间的相似性效果可能会更加显著。因此,本文利用关键词间点互信息,结合CLSVSM的构造思想,提出了用关键词间最大点互信息代替最大共现强度,进而对VSM中0值填补,实现了基于点互信息的CLSVSM的构造。
3.2 语义增强的CLSVSM
在CLSVSM中,通过对VSM中0位置的补充,使得文献主题聚类的精度得到了一定的提高。本文旨在利用点互信息和关键词共现向量,提取关键词间潜在语义相似度,并对VSM中每个布尔权重进行语义上的修正,使得各关键词在整体上对文献聚类的贡献得到重新分配,进而提出语义增强的CLSVSM。在构建新模型时延用CLSVSM构建时的符号体系。语义增强的CLSVSM的具体表达式如式(9)所示:

该表达式在形式上与CLSVSM相同,不同的是本文将各维的权重重新分配,使得各个特征词在文本中均有所体现,并提出新权重的计算方法,如式(10)所示:
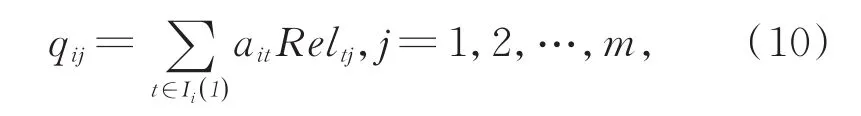
式中,ait表示第i篇文献中第t个关键词的布尔权重,Reltj表示第j,t个关键词间的语义相似度。
该模型使得与文献主题相关的关键词的权重提高,而与文献主题无关关键词的权重降低,即在传统的模型中直接嵌入关键词间的潜在语义相似关系。在某种程度上,相当于对语义关系的二次提取挖掘,即关键词间潜在语义相似关系的提取和文献关键词间语义关系的提取。
4 模型检验
4.1 数据来源
本实验采用中、英文三个数据集,分别对基于点互信息的CLSVSM、语义增强的CLSVSM、CLSVSM、VSM以及word2vec模型进行实验,并对其结果进行比较。
实验所采用的中文数据均来自CNKI。其中一类采集于信息科技下的“出版”“图书情报与数字图书馆”“档案及博物馆”,每个学科按被引频次降序排列各收集300篇文献,经过简单的预处理,即去除不含关键词的文献,共获得文献895篇,其中包含“出版”296篇、“图书情报与数字图书馆”299篇和“档案及博物馆”300篇,同时共获得关键词2024个;另一类数据采用多类别不均衡数据,采集于“出版”“图书情报与数字图书馆”“档案及博物馆”“基础科学”和“医药卫生科技”五个类别,每个类别学科收集400篇文献,经过处理,即去除不含有关键词的文献,去除关键词词频小于2的关键词,最终获得文献共1 739篇,其中“出版”360篇、“图书情报与数字图书馆”369篇、“档案及博物馆”344篇、“基础科学”286篇、“医药卫生科技”380篇,共包含关键词1 128个。
英文数据采集于web of science,其中包括“computer science information system”,“management”,“computer science interdisciplinary applications”三个类别,分别含 234篇、123篇、54篇文献,共收集1 889个关键词。
4.2 评价指标
在文本聚类、分类领域中,往往希望找到一种完美的聚类算法使文本得到精准分类,然而在实际情况中各种聚类算法难免存在偏差,这就使得我们需要对聚类算法进行评价。本实验采用信息检索和机器学习领域常用的性能指标[28]:纯度(purity)、熵值(entropy)、F1值,以下对其进行简单的说明:
B-Cubed方法是信息抽取的评价指标[18],其通过计算每类的准确率和召回率,加权平均求得整体的准确率和召回率,进而求得调和均值,即F1。而另外两个评价指标纯度和熵值则可由gCLUTO平台聚类直接获得。
纯度、熵值及F1的取值均介于0和1之间,聚类之后最好的结果就是文献数据的原分类和实验之后的分类达到一致,即纯度和F1值越大越好,熵值越小越好。
4.3 实验过程
实验中,我们首先用VSM、CLSVSM在三个数据集上分别进行多次实验,并记录各实验结果,期间用到VBA、R、gCLUTO软件,然后用基于点互信息的CLSVSM和语义增强的CLSVSM进行实验。两个新模型的提出都是基于CLSVSM,因而将CLSVSM的聚类结果作为一个基准来衡量基于点互信息的CLSVSM和语义增强的CLSVSM的聚类结果的优劣。最后,引入word2vec模型,实验时,我们采用word2vec分别对以上三个数据集进行训练,得到每个关键词的词向量,并将词向量间的欧氏距离定义为关键词之间的相似度,再进行聚类。然后比较基于点互信息语义增强的CLSVSM、语义增强的CLSVSM以及word2vec模型的聚类效果。
实验过程将分为两部分。第一部分:各模型在三个数据集上进行多次实验后,计算各指标的均值和标准误,以对模型的整体聚类效果进行分析;第二部分:以第二个中文数据集为例,将各模型多次实验的纯度和熵值分别绘制为折线图,进行比较,以对各模型的效果有一个直观的比较。
4.4 实验结果
本文将基于点互信息的CLSVSM、语义增强的CLSVSM、CLSVSM、VSM以及word2vec模型分别在三个数据集上进行比较,每种模型均进行多次实验。其中,第一部分实验的结果如下表1-表3所示,第二部分的实验结果如图1和图2所示:

表1 各模型在第一个中文数据集(三类)上的实验结果比较Table 1 Comparison among experimental results of the models on the first Chinese dataset(three types)

表2 各模型在第二个中文数据集(五类)上的实验结果比较Table 2 Comparison among experimental results of the models on the second Chinese dataset(five categories)

表3 各模型在英文数据集上的实验结果比较Table 3 Comparison among the experimental results of the model on English dataset

图1 各模型的纯度折线图Fig.1 Line chart of purity for each model
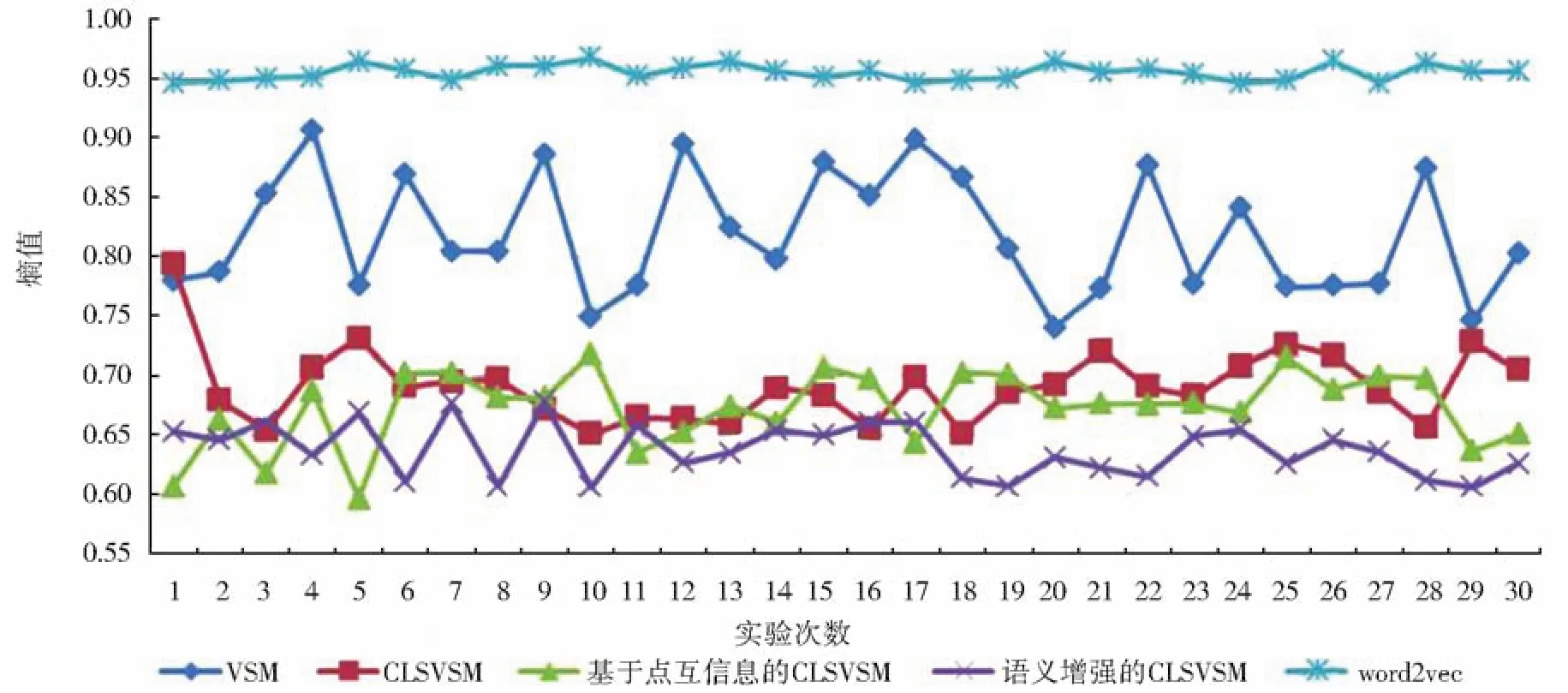
图2 各模型的熵值折线图Fig.2 Line chart of entropy of each model
由表1可知:语义增强的CLSVSM各评价指标的结果均优于CLSVSM,其中,纯度和F1值分别提高了2.3%和2%,熵值下降了3.7%,聚类精度明显提高,这是因为语义增强的CLSVSM在构建过程中分别提取了关键词间的潜在语义相似关系以及文献与关键词间的语义关系,较CLSVSM提取了更多的语义关系,最终表现出良好的聚类性能;而基于点互信息的CLSVSM在构造过程中虽然植入了提取出的语义相似性,但其作用与共现强度相近,因而表现出的聚类效果与CLSVSM相当。语义增强的CLSVSM和基于点互信息的CLSVSM的聚类效果同样较word2vec的聚类效果优良。
表2所示实验中,各模型的纯度值低熵值高,可能是因为实验所采用数据集为多类别不均衡数据集,所选文献集分布较散所造成的。但是在聚类效果上,各模型在该数据集与第一个中文数据集上的表现一致。其中,语义增强的CLSVSM的纯度和F1值分别较CLSVSM提高了10.2%和9.2%,而熵值降低了8.5%,同样表现出很好的聚类效果。此外,基于点互信息的CLSVSM和语义增强的CLSVSM的聚类效果均优于word2vec。
由表3可知,语义增强的CLSVSM相对于CLSVSM虽然其纯度值比较接近,但是F1值显著提高了12.3%,说明在该英文数据集中,语义增强的CLSVSM对文献聚类精度的提高仍然起到了一定的作用。同样,语义增强的CLSVSM的聚类精度高于word2vec。
由图1和图2可知:语义增强的CLSVSM的纯度和熵值在30次实验过程中均逐渐趋于稳定,其中纯度、熵值曲线并较其他曲线分别处于最高、最低位置;而基于点互信息的CLSVSM和CLSVSM的纯度、熵值曲线均相互交织,不相上下,但均值曲线均高于word2vec,熵值曲线均低于word2vec。
CLSVSM、基于点互信息的CLSVSM、语义增强的CLSVSM相对于传统的VSM均在各模型中添加了语义信息。实验采用中、英文三个不同类别的数据集,综合图表信息可知,三个模型在聚类精度上都较VSM有提高。而且,语义增强的CLSVSM在不同数据集上表现出一致的,较CLSVSM、word2vec聚类精度明显提高的效果,检验了该模型的稳定性及适用范围的广泛性。之所以语义增强的CLSVSM显著提高了聚类精度,原因在于该模型不仅提取了关键词间的潜在语义关系,还进一步挖掘了文献与关键词间的关系,使潜在语义关系得到二次挖掘,最终达到显著增强聚类效果的目的。以上结果有力地证明了提取挖掘关键词间语义关系可以明显提高文献聚类的性能。语义增强的CLSVSM聚类效果明显优于word2vec,进而说明基于点互信息提取出的关键词间潜在相似性要比采用word2vec计算出的相似性更能获得重要的信息,也更加符合实际。另外,本文对基于点互信息的CLSVSM、语义增强的CLSVSM及word2vec各自算法的时间复杂度进行了研究。在时间复杂度中多用大O符号表示法,即T(n)=O(f(n)),其中f(n)表示每行代码执行次数之和,而O表示同阶关系。对三个模型的复杂度进行研究,基于点互信息的CLSVSM的时间复杂度为:T1(n)=O(n2),语义增强的CLSVSM的时间复杂度为:T2(n)=O(n3),word2vec的时间复杂度为:T3(n)=O(mlogn),其中,n为关键词的个数,m为语料库大小。因为实际中m≫n,故三者间的大小关系为T3>T2>T1。因而,语义增强的CLSVSM和基于点互信息的CLSVSM在时间复杂度上均较word2vec简单,便于模型的推广。
5 结论
语义相似性度量作为信息资源检索、文献主题聚类领域的关键技术受到极大的重视。语义信息是否充分提取将直接影响文献聚类的结果。CLSVSM虽挖掘了共现潜在语义,但仍有很大的改进空间。
本文将语义相似性度量技术应用于文献主题聚类,在CLSVSM的基础上,利用点互信息计算关键词间语义相似度,提出基于点互信息的CLSVSM。同时,还通过潜在语义分析修正布尔权重,提出语义增强的CLSVSM,并与word2vec模型进行对比实验。经实验检验:基于点互信息的CLSVSM与原CLSVSM的聚类效果相当;语义增强的CLSVSM较CLSVSM有良好的聚类效果,能更好地度量文献之间的主题相关性。在利用word2vec模型进行语义相似度计算的对比实验中,基于点互信息的CLSVSM、语义增强的CLSVSM的聚类效果均明显优于word2vec。因此语义增强的CLSVSM可作为一种新的算法应用于信息检索、文献分类与聚类等领域,推进信息资源利用的有效性和高效性。此后,我们将会对本文提出的两种新模型扩展到三元共现的情况并评价其效果。
