Brauer特征标三元组及其诱导子

黄谦，郭鸿

（山西大学 数学科学学院，山西 太原 030006）

0 引言

在有限群的复表示论与模表示论中，Clifford理论均属于核心内容，它研究正规子群与大群的表示论之间的联系。设G为任意有限群，N为G的正规子群，θ∈Irr(N)为N的一个不可约复特征标，并且θ是G-不变的，则称(G，N，θ)为一个特征标三元组，该定义出现在Isaacs的特征标经典教材[1]中第186页。类似地，固定一个特征为素数p的代数闭域，通常记IBr(N)为N的关于素数p的所有不可约Brauer特征标的集合，如果φ∈IBr(N)也是G-不变的，则称(G，N，φ)为一个模特征标三元组，该定义见Navarro模表示教材[2]中定义8.25，在本文中我们称之为Brauer特征标三元组。事实上，关于特征标三元组，无论是复特征标还是Brauer特征标，不仅本身获得了很多深刻的结果，而且为解决表示论中的重要问题提供了有效的技术。在特征标三元组的研究中，诱导子是一个重要的概念，其意义在于给出了某种规范的从而是较好控制的特征标诱导过程。设T=(G，N，θ)为一个特征标三元组，χ∈Irr(G)，选定M⊲G且M⊆N，α是χM的一个不可约分量，设T=Gα，由Frattini推理可知，有G=NT，又因为N∩T=Nα为α在N中的惯性群，由Clifford对应可知，存在唯一的η∈Irr(Nα|α)，使得ηN=θ。

设T=(G，N，θ)为一个特征标三元组，由上知，存在S=(H，M，φ)也是一个特征标三元组，满足条件NH=G，N∩H=M，φN=θ，则称S为T的一个诱导子。关于特征标三元组诱导子的研究，Dade在[3]中获得了一系列深刻结果，但主要定理的证明复杂且艰深，特别是Dade还探讨了任意特征为0的域上的特征标三元组。为了简化Dade关于特征标三元组诱导子的深刻定理，Isaacs在[4]中考虑复数域上的特征标三元组，引入了拟本原的诱导子等基本概念（见本文第1节预备知识），证明了Dade定理（即[3]中定理8.1）的复特征标版本。方便起见，如果T=(G，N，θ)为一个特征标三元组或Brauer特征标三元组，我们记degT=θ(1)，称为T的次数。

以下是Isaacs在文献[4]中的主要结果，即该文定理3.1。

定理 1（Isaacs）设T=(G，N，θ)为特征标三元组，Si=(Hi，Mi，φi)为T的拟本原诱导子，其中i=1，2，如果N是幂零群，则 |H1|=|H2|，等价于说degS1=degS2。

作为上述定理的一个应用，Isaacs证明了下述重要结论，即该文的定理B：如果χ∈Irr(G)可从子群H≤G的某个本原特征标θ∈Irr(H)诱导，即χ=θG，则θ(1)为诱导χ的一个本原特征标次数。一般而言，不可约复特征标有很多不全相等的本原诱导次数，研究这些本原诱导次数何时都相等，是特征标诱导理论中的基本问题之一。在[5]中，作者对此问题做了若干探讨，该文的参考文献也包含了特征标三元组的诱导子及其应用的相关重要论文。

定理2（Isaacs）设G为有限群且χ∈Irr(G)，如果χ在G的Fitting子群F(G)上的限制不可约，则诱导χ的所有本原特征标均有相同的次数。

本文将研究上述两个定理的Brauer版本，即对Brauer特征标三元组证明相应的结论。因为Brauer特征标通常不满足复特征标理论中的Frobenius互反率，这给我们在证明中造成很多技术上的困难。我们将考虑p-可解群，以便使用Fong-Swan关于Brauer特征标的提升定理，但更为精致的也是最新的提升技术，即Bπ-提升和Dπ-提升，出现在Isaacs创立的π-理论中，见文献[6]。因此，我们在本文最后一节将证明上述两个Isaacs定理的π-理论版本，通过取素数集合π={p}′为素数p的余集，即可得到下述关于Brauer特征标的相应定理。

定理3设G为p-可解群，其中p为任意素数，并且T=(G，N，θ)为一个Brauer特征标三元组。如果N是幂零群，则T的任意两个拟本原诱导子具有相同的次数。

定理4设G为p-可解群，其中p为任意素数，并且φ∈IBr(G)在G的Fitting子群F(G)上的限制不可约，则诱导φ的所有本原Brauer特征标均有相同的次数。

事实上，特征标三元组的诱导子之所以重要，一个关键的事实是能提供一个诱导双射。具体讲，如果S=(H，M，φ)是特征标三元组T=(G，N，θ)的一个诱导子，则特征标的诱导ξ↦ξG可定义一个双射：Irr(H|φ)→ Irr(G|θ)，不妨称之为诱导子对应。这是一个应用广泛的结论，见文献[6]，但该结果一般对Brauer特征标不成立。借助于Lewis关于次正规诱导源的一个定理，即[7]中的定理A，我们得到了所需的诱导子对应的Brauer版本。当然，我们在本文实际证明的是更为一般的结论，即诱导子对应的π-版本。

定理5设G为p-可解群，其中p为任意素数，T=(G，N，θ)为一个 Brauer特征标三元组，并且S=(H，M，φ)为其一个诱导子。如果M⊲⊲N为N的次正规子群，则Brauer特征标的诱导ξ↦ξG给出一个双射：Irr(H|φ)→ Irr(G|θ)。

因为幂零群的每个子群都是次正规子群，故定理3中存在上述诱导子对应。此外，本文使用的群论和特征标理论的术语和符号，可分别参考Isaacs的群论教材[8]和特征标教材[1]，关于 Brauer特征标的基本概念和性质，均来自Navarro的专著[2]。

1 预备知识

我们先给出Isaacs的π-部分特征标的概念，细节可参考[6]。

设G为π-可分群，其中π按照惯例表示一些素数构成的集合，记G0为G的所有π-元素构成的集合。如果χ为G的复特征标，则记χ0为χ在G0上的限制，称为χ的π-限制，此时称χ0为G的一个π-部分特征标。进而，如果π-部分特征标χ0不能写成两个π-部分特征标之和，即χ0≠α0+β0，其中α，β为G的复特征标，则称χ0为G的一个不可约π-部分特征标，简称为G的Iπ-特征标，全体记为Iπ(G)。值得指出的是，当π取某个素数p的余集时，则π-部分特征标即通常关于素数p的Brauer特征标，Iπ-部分特征标为不可约 Brauer特征标，即Iπ(G)=IBr(G)。由此，可以认为π-部分特征标统一了通常的复特征标和p-可解群的Brauer特征标。

如果N⊲G，并且θ∈Iπ(N)为G-不变的，则称T=(G，N，θ)为一个Iπ-特征标三元组。我们记degT=θ(1)，称为T的次数。再设S=(H，M，φ)为一个Iπ-特征标三元组，如果满足条件NH=G，N∩H=M且φN=θ，则称S为T的一个诱导子。进而，如果对每个K⊲H且K≤M，均有φK是齐次的，则称S是拟本原的。

为了使用Fong-Swan提升技术，Isaacs定义了Bπ-特征标集合Bπ(G)⊆ Irr(G)作为Iπ(G)的一种典范提升，即π-限制χ↦χ0给出了一个双射：Bπ(G)→Iπ(G)。但Bπ-特征标的定义相当复杂，并且不易识别，为此Isaacs引入了关于G和π的域自同构，可给出2∈π时的一个有效判别条件。下面是文献[6]的定理5.2。

引理 1（Isaacs）设G为π-可分群，2∈π，并且τ为关于G和π的域自同构。如果χ∈Irr(G)χτ=χ，则χ∈Bπ(G)当且仅当χ0∈Iπ(G)。

在剩下的情形即2∉π时，Bπ-特征标的表现和性质难以控制，但Isaacs在[9]和[10]中根据Dade的想法引入了Dπ-特征标的概念，也唯一定义了一个子集Dπ(G)⊆ Irr(G)，作为Iπ-特征标的一种典范提升，并且特征标的π-限制χ↦χ0同样定义了一个双射Dπ(G)→Iπ(G)。因为Dπ-特征标的定义涉及所谓的π-标准符号特征标δ(G，H)，对任意子群H≤G，还有特征标的π-诱导θπG=(δ(G，H)θ)G，对任意θ∈Irr(H)，我们难以在此精准给出复杂的概念和性质，可参考最新文献[6]或上述两篇相关文献。

我们将用到下述Dπ-特征标的判别条件，即著名的Dade定理，见文献[10]的定理E。

引理2（Isaacs）设G为π-可分群且2∉π，如果H≤G，θ∈Irr(H)和χ∈Irr(G)，满足θπG=χ，则θ∈Dπ(H)当且仅当χ∈Dπ(G)。

在证明定理5时，我们要用到诱导源的概念。设G为任意有限群，称(H，θ)为G的一个特征标对，如果H为G的子群且θ∈Irr(H)。因为G按共轭可作用在其所有特征标对构成的集合上，即对任取g∈G，定义 (H，θ)g=(Hg，θg)，其中θg(hg)=θ(h)，任意h∈H，我们记(H，θ)或θ在G中的稳定子群为显然Gθ≤NG(H)，并且Gθ即为θ在NG(H)中通常的惯性群。作为正规子群上特征标Clifford对应的推广，如果特征标的诱导ξ↦ξG可定义从 Irr(Gθ|θ)到 Irr(G|θ)的一个双射，则称(H，θ)为G的一个诱导源。相关定义和性质可见文献[7]。

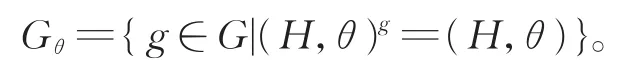
2 主要结果

为了证明本文的主要结果，我们需要引入一个技术性概念。

定义1设G为π-可分群，并且η∈Iπ(G)。当2∈π时，记为η的Bπ-提升；而当 2∉π时，记为η的Dπ-提升，则称为η在G中的标准提升。

下述为本文定理3的π-版本。

定理6设G为π-可分群，T=(G，N，θ)为一个Iπ-特征标三元组。如果N是幂零群，则T的所有拟本原诱导子均有相同的次数。

证明 设∈Irr(N)为θ的标准提升，根据标准提升的典范唯一性，可知也是G-不变的，从而=(G，N，)为一个复特征标三元组。再设S=(H，M，φ)为T的任意一个诱导子，按定义，则NH=G，N∩H=M，并且φN=θ。设∈Irr(M)为φ∈Iπ(M)的标准提升，同理可知也是H-不变的，从而(H，M，)为特征标三元组。下面我们区分两种情形讨论。

（1）假设2∈π。此时按定义均为Bπ-特征标，设τ为关于G和π的域自同构，则，从而，根据引理 1 可知也是θ的Bπ-提升，故，表明是的诱导子。

验证也是拟本原的。任取K⊲H且K≤M，从S的拟本原性可知φK是齐次的。因为是Bπ-特征标，熟知的每个分量都是Bπ-特征标，并且不同的Bπ-分量在K0上的限制也是两两不同的Iπ-特征标，据此可知也只能是齐次的，即证的拟本原性。

（1）采用组合投资方法。也被称作是多样化投资，分为两种不同的情况。第一种就是将资金有选择性地放到多个项目上，降低未来风险。比如安居工程就是当前十分热门的项目类型，就可以将资金放在这类项目上。另一种方式是按照所投资项目资金的情况，将资金按照不同的比例投放在房地产、股票债券、银行存款安全性高、房地产投资可以获得良好的收益。想要确保投资具备流动性、收益性以及安全性等，必须要开展相关的投资组合，对资金的流量以及流向等进行合理安排。

根据Isaacs定理1，可知的所有拟本原诱导子均有相同的次数，即degS=deg是不变量，与S的不同选取无关，故所证结论在2∈π的情形成立。

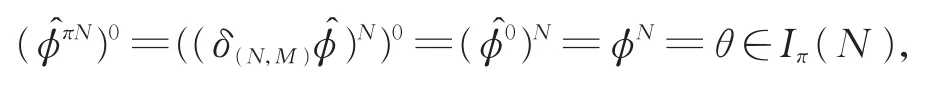
（2）假设2∉π。此时和按定义均为Dπ-特征标，注意到(δ(N，M))0=1M0，故根据引理 2可知也是θ的Dπ-提升，故=，表明=(H，M，δ(N，M))为的诱导子。

验证也是拟本原的。任取K⊲H且K≤M，从S的拟本原性可知φK是齐次的。因为是Dπ-特征标，熟知的每个分量都是Dπ-特征标，并且不同的Dπ-分量在K0上的限制也是两两不同的Iπ-特征标，据此可知也只能是齐次的。但K⊲M，熟知K必然包含在π-标准符号特征标δ(N，M)的核里，所以(δ(N，M))K=也是齐次的，表明是拟本原的。

根据Isaacs定理1，可知的所有拟本原诱导子均有相同的次数，即degS=φ(1)=deg是不变量，与S的不同选取无关，故所证结论在2∉π的情形也成立。作为应用，我们可得到Isaacs定理4的π-版本。

定理7设G为π-可分群，如果η∈Iπ(G)在G的Fitting子群F（G）上的限制不可约，则诱导η的所有本原的Iπ-特征标均有相同的次数。

证明令N=F（G），θ=ηN，则θ是G-不变的Iπ-特征标，故T=(G，N，θ)为一个Iπ-特征标三元组。设ξG=η，其中H≤G且ξ∈Iπ(H)为本原的Iπ-特征标。我们要证明的是诱导η的本原Iπ-特征标ξ的次数ξ(1)与H和ξ的不同选取无关。再令M=N∩H和φ=ξM，则φ显然是H-不变的。

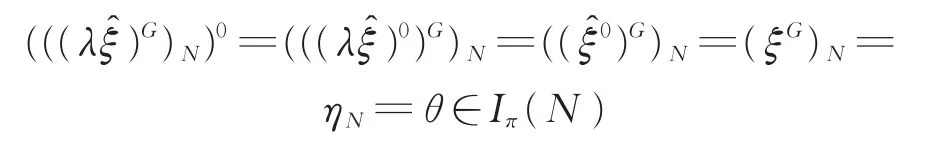
为不可约Iπ-特征标，故 (()G)N必然是不可约的复特征标，根据Mackey定理，则NH=G。又因为M=N∩H显然是H的正规子群，故从π-标准符号特征标的性质（见[8]中定理 2.5（d））可知M≤Ker(δ(G，H))，更有M≤ Kerλ。再次使用Mackey定理，我们又有

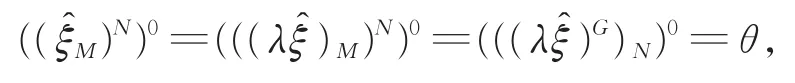
我们断言φ∈Iπ(M)且φN=θ，据此可知S=(H，M，φ)为Iπ-特征标三元组，并且是T=(G，N，θ)的诱导子。当 2∈π时，按定义为Bπ-特征标，根据引理 1，则τ=，不难看出 (M)N在域自同构τ下也是不变的，故为Bπ-特征标，表明 (M)N=恰为θ的Bπ-提升。进而，从为Bπ-特征标且M⊲H，可知M∈Irr(M)也是Bπ-特征标，并且 (M)0=ξM=φ∈Iπ(M)，同理可知M也是φ的Bπ-提升 ，即M=。 所 以=，两边取π-限制得到φN=()0=0=θ，表明断言成立。当2∉π时，按定义为Dπ-特征标，此时

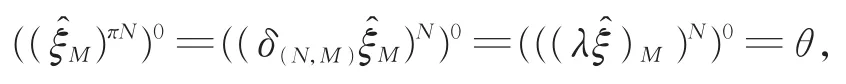
下面验证S是拟本原的。任取K≤M且K⊲H，已知ξ∈Iπ(H)是本原的，从Iπ-特征标的Clifford定理可知ξ也是拟本原的，故φK=ξK是齐次的，按定义可知S是拟本原的。

最后，注意到degS=φ(1)=ξ(1)，根据定理6，则的所有拟本原诱导子S均有相同的次数，由此表明ξ(1)与ξ和H的不同选取无关，故所证结论成立。

在上述两个定理中，选取π={p}′为素数p的余集，按前述说明，此时G为p-可解群，并且Iπ(G)=IBr(G)，即得本文的定理 3和定理 4。

最后证明本文的定理5的π-版本，为此，我们需要Lewis的一个定理，见文献[7]的定理A。

引理3（Lewis）设G是π-可分群，S⊲⊲G为G的次正规子群且φ∈Iπ(S)。如果(S，)为G的一个诱导源，其中∈ Irr(S)为φ的标准提升，则Iπ-特征标的诱导为双射，其中表示在G中的稳定子。

定理 8设G是π-可分群，T=(G，N，θ)为Iπ-特征标三元组，并且S=(H，M，φ)为其一个诱导子。如果M⊲⊲N，则Iπ-特征标三元组的诱导给出一个双射：

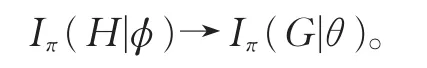
证 明设∈Irr(N)和∈Irr(M)分 别 为θ∈Iπ(N)和φ∈Iπ(M)的标准提升，类似定理 6的证明，同理可证当 2∈π时，则=；当 2∉π时，则(δ(N，M))N==。显然和分别是H-不变的和G-不变的。如果 2∈π，(H，M，)也是特征标三元组(G，N，)的一个诱导子，故特征标的诱导为双射：Iπ(H|)→Iπ(G|)，表明 (M，)为G的一个诱导源。如果2∉π，根据π-标准符号特征标的性质（见文 献[6]中引理 2.33（c）），则δ(G，H)∈Irr(H)是δ(N，M)∈ Irr(M)的扩张，从而δ(N，M)为H-不变的。此时δ(N，M)也是H-不变的，故 (H，M，δ(G，H))也是特征标三元组的(G，N，)的一个诱导子，所以特征标的诱导也是双射：Iπ(H|δ(N，M))→Iπ(G|)。 根据Gallagher对应（见[1]中推论6.17），则Iπ(H|δ(N，M))=δ(G，H)Irr(H|)，表明特征标的诱导也是双射：Iπ(H|)→Iπ(G|)，故 (M，)也是G的诱导源。至此可使用上述Lewis定理，即引理3，我们有Iπ-特征标的诱导所定义的双射 ：Iπ(H|φ)→Iπ(G|φ)。

剩下的只需证明Iπ(G|φ)=Iπ(G|θ)，为此，我们先证明Iπ(N|φ)={θ}。如果M⊲N，因为φN=θ，故Nφ=M，根据Iπ-特征标的 Clifford对应得到Iπ(N|φ)={θ}。一般地，如果M在N中不正规，因为M是N的次正规子群，故存在M⊲L⊲⊲N，其中M＜L≤N，特别地，令α=φL，则α∈Iπ(L)，故Iπ(L|φ)={α}。任取ψ∈Iπ(N|φ)，则ψ必然在α上方，通过对 |N：M|做归纳法，现在 |N：L|＜ |N：M|，故对L⊲⊲N。由归纳假设得ψ=αN=φN=θ，即证Iπ(N|φ)={θ}。该公式表明G的每个Iπ-特征标，只要在φ的上方，必然也在θ的上方，即Iπ(G|φ)⊆Iπ(G|θ)。因为反包含关系显然成立，故Iπ(G|φ)=Iπ(G|θ)。

同理，选取π={p}′为素数p的余集，则G为p-可解群且Iπ(G)=IBr(G)，定理得证。