软件缺陷预测模型超参数的稳健优化方法

2021-05-19崔军丁浩杰王瑞波李济洪

山西大学学报（自然科学版） 2021年2期

崔军，丁浩杰，王瑞波，李济洪

（1.山西大学计算机与信息技术学院，山西太原 030006；2.山西大学现代教育技术学院，山西太原 030006）

0 引言

作为软件工程领域的主要任务之一，软件缺陷预测的主要目的是利用机器学习方法预测出当前开发的软件中的缺陷模块，为后续的高效测试提供重要基础[1-6]。软件缺陷预测任务主要分为两个子任务：（1）跨版本预测子任务：指使用软件项目的历史版本数据构建预测模型，来预测当前版本中的缺陷模块；（2）跨项目预测子任务：指使用其他软件项目的源代码构建模型来预测当前项目的缺陷模块。当软件项目的历史版本数据充足时，子任务（1）所构建的软件缺陷预测模型常被使用。不过，很多软件项目在开发初期，不具备充足的历史版本数据。此时，子任务（2）所构建的预测模型常被用来预测项目中的缺陷模块。本文的研究涵盖了这两个子任务。

在软件缺陷预测任务中，机器学习算法被广泛用于建模过程。所构建的软件缺陷预测模型的性能不仅依赖于机器学习算法的类型，也依赖于机器学习算法中超参数的设置[7-8]。目前，包含支持向量机[1-2]，随机森林[3]，神经网络[4-5]等在内的主流机器学习算法已在软件缺陷预测任务中被深入探讨。其中，基于集成学习的软件缺陷预测模型[9-13]取得了不错的性能。具体地，通过对软件缺陷预测数据进行多次重抽样，多个训练样本集可以被获得。进而，支持向量机等主流分类算法被应用在多个训练样本集上，生成多个软件缺陷预测模型。最终，这些软件缺陷预测模型可以通过众数投票方法形成一个集成的软件缺陷预测模型。实际上，基于集成学习的软件缺陷预测模型的性能明显依赖于单个软件缺陷预测模型的性能。因此，如何优化单个分类算法中的超参数，是提升基于集成学习的软件缺陷预测模型性能的主要问题之一。

常用的超参数优化方法，主要关注软件缺陷模型的平均性能，并不关心软件缺陷预测模型性能的变异性。这会导致软件缺陷预测模型的性能变差很多，不利于该模型在新软件模型上的稳定预测。为此，本文提出一种超参数的稳健优化方法。该方法不仅关注软件缺陷预测模型的平均性能，而且使用标准差来度量模型的稳健性。进而，该方法使用信噪比作为优化目标，寻求超参数的最优取值，以构建性能优良的软件缺陷预测模型。

为了验证超参数的稳健优化方法的有效性，本文采用支持向量机作为集成学习的基分类器，使用块正则化m×2交叉验证方法[14]作为重抽样方法，构建了一种基于集成学习的软件缺陷预测基线模型。进而，采用稳健优化对该基线模型中支持向量机的两个超参数（方差参数和松弛参数）进行调优，并与基线模型的预测性能进行比较。本文在10个软件项目的20个版本上构建了软件缺陷预测实验，并使用F1值度量模型的性能。实验结果表明，基于稳健优化的超参数选择方法可以有效地提高软件缺陷预测模型的性能。

1 软件缺陷预测模型超参数的稳健优化方法

1.1 基于集成学习的软件缺陷预测模型

对于单个软件项目，将其软件缺陷预测数据集记为Dn=｛（xi，yi）｝（i=1，…，n）。其中，第i条记录对应软件项目中的第i个模块。xi表示模块i的度量向量，用来量化模块i的源代码的特性。常用的度量指标在表1中给出。yi表示模块i是否有缺陷，为一个二值变量。yi=1表示模块i为有缺陷模块，相应的记录被称为正例；反之，yi=0表示模块i不含缺陷，相应的记录被称为负例。显然，软件缺陷预测任务可以形式化为如式（1）所示的二类分类问题。

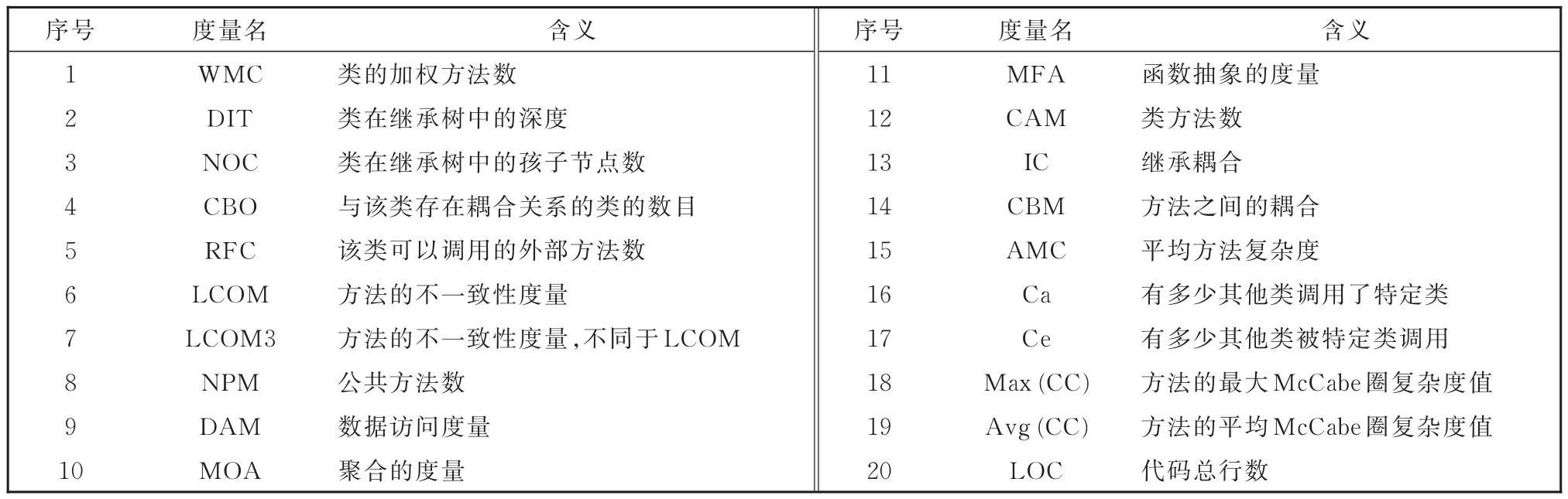
表1 软件缺陷预测任务中常用的度量集合Table 1 Commonly used metrics in software defect prediction task

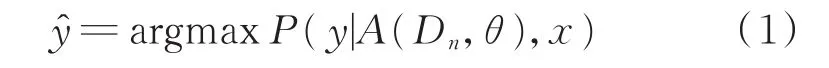
其中，A（Dn，θ）为某一分类算法A在数据集Dn上构建的软件缺陷预测模型，θ为算法A中所含的超参数集合。z=（x，y）为独立于Dn的一个新的软件模块记录。通常y是未知的，因此，需要将模型A（Dn，θ）作用在x上对y进行预测，其预测值为。显然，超参数集合θ的取值对模型的性能有着明显的影响。

本文采用集成学习算法，将块正则化m×2交叉验证方法和支持向量机进行融合，来构建一个软件缺陷预测模型A（Dn，θ）。模型的轮廓图见图1，其中，“m×2 BCV”代表块正则化m×2交叉验证方法，“RUS”代表随机下采样方法，“Tm”和“Vm”分别代表第m次切分下对应的训练集和验证集，“Tum”和“Vum”分别为“Tm”和“Vm”进行下采样之后的训练集和验证集结果，“SVM（X）”和“Pred（X）”则分别代表使用X数据集训练而得到的SVM模型和其预测结果，“Majority Voting”代表众数投票法，“Predictions”表示的是使用众数投票法集成后的最终结果。整个模型具体分为如下4个步骤。

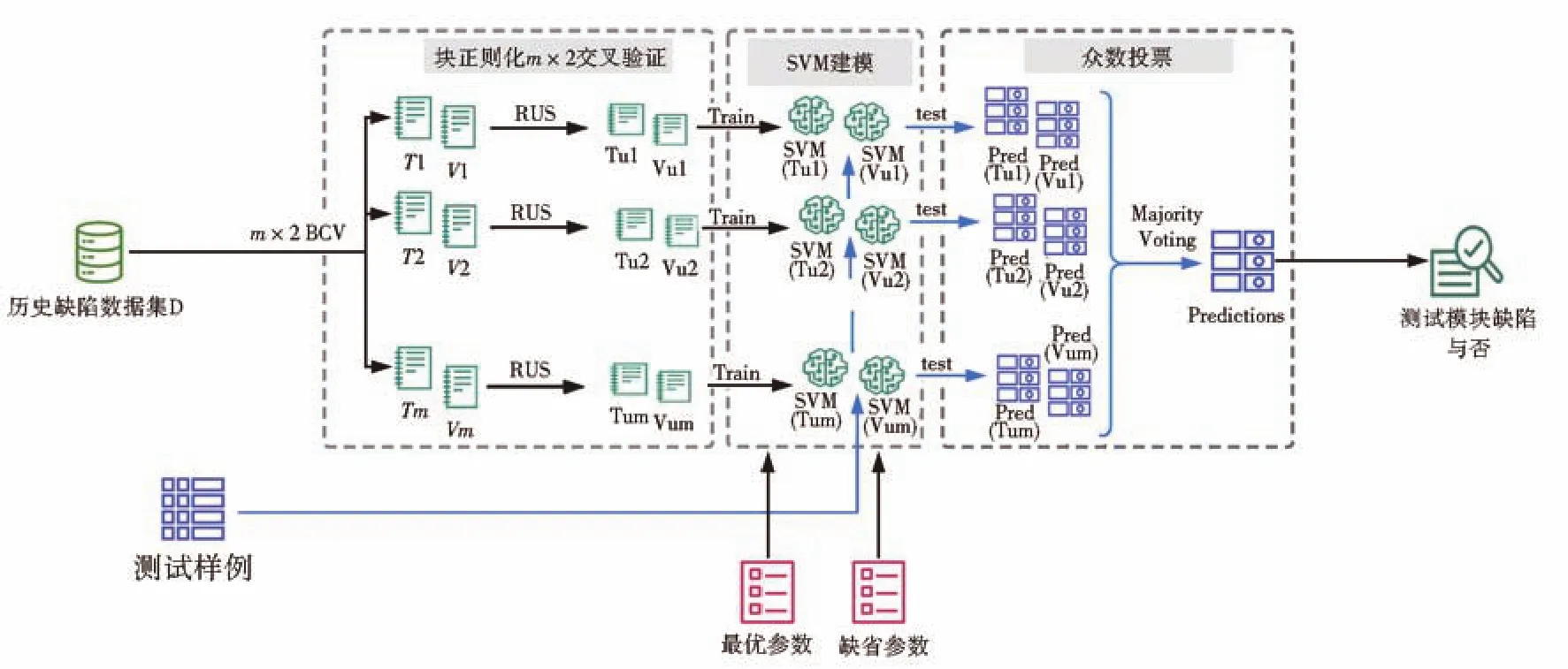
图1 基于集成学习的软件缺陷预测模型框图Fig.1 Sketch plot of software defect prediction model based on ensemble learning

（1）采用块正则化m×2交叉验证方法将数据集Dn切分成m组训练集，每一组训练集包含两个大小为n/2且完全不相交的训练集。任意两组之间，训练集间重叠的记录个数均相同。也就是说，从重叠记录个数来看，这m组训练集是“均衡”的。

（2）在m组训练集上实施随机下采样方法。由于训练集中正例所占比例较小，随机下采样方法随机去除掉训练集中的负例样本，使正例和负例样本所占比例均衡。在随机采样过程中，马氏距离用来度量同一组内两个训练集间的分布距离。马氏距离较小的下采样样本被优先考虑。

（3）在下采样后的m组训练集上，使用支持向量机训练形成2m个软件缺陷预测模型。根据块正则化m×2交叉验证的性质可知：1）由于m组训练集来自同样的总体，2m个软件缺陷预测模型的性能是基本相同的；2）由于m组训练集是均衡的，2m个软件缺陷预测模型间的相关性也是相同的，并且是最小的。这两点优良性质为后续的集成奠定了良好的基础。

（4）对于2m个软件缺陷预测模型，采用众数投票的方法进行集成。具体地，当预测新的软件模块是否有缺陷时，先使用构建好的2m个软件缺陷预测模型对该模块分别预测，形成了2m个预测结果。如果预测结果认为该模块有缺陷的票数不少于一半时，则判定为缺陷模块；否则，判定该模块不含缺陷。

容易看出，上述基于集成学习的软件缺陷预测模型的性能明显优于支持向量机基分类器的性能。在常用的支持向量机算法中，方差参数（Gamma）和代价参数（Cost）是两个重要的超参数。因此，如何优化这两个超参数的取值，是改善本文所提模型的性能的关键所在。

1.2 超参数的稳健优化算法

本文采用稳健设计的方法来优化方差参数和代价参数θ=（Gamma，Cost）的取值。稳健设计是统计实验设计中的一种重要优化方法，其主要用于设计电子产品的参数，使得产品的性能指标稳定。稳健设计在关注性能指标期望改善的同时，也关注其方差的变化，并能够减小模型的波动。

本文采用块正则化m×2交叉验证来估计软件缺陷预测模型的性能。假设软件缺陷预测模型性能的m×2 交叉验证估计为，且假设越大，模型的性能越优。的形式如下：

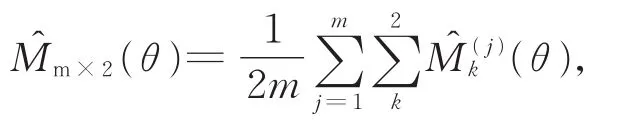
其中，θ*为θ在望大特性下的最优值。然而，上式不能直接进行梯度优化。因此，本文使用网格搜索的方法在参数集合θ的多组取值中寻求近似的最优值。

支持向量机的两个超参数Gamma和Cost的取值默认为1。对于这两个参数，本文在候选取值集合｛0.5，0.75，1，1.25，1.5｝中寻求它们的最优值。因为该候选取值集合的大小为5，因此，两种参数共可组成52=25种候选取值。

2 实验数据及设置

2.1 实验数据

本文采用了10个常用的软件缺陷预测项目，共计涵盖了26个软件版本。这些项目数据均来自于PROMISE数据库。软件缺陷数据集的详细信息见表2。这些软件缺陷预测数据集的度量集合见表1，有关这些指标的详细解释，请参阅文献[15]的表II。这些数据和度量变量之前已被广泛使用[16-18]。从表2可以看出，不同版本的软件项目的缺陷率分布在8%～53%之间，变化范围较大。

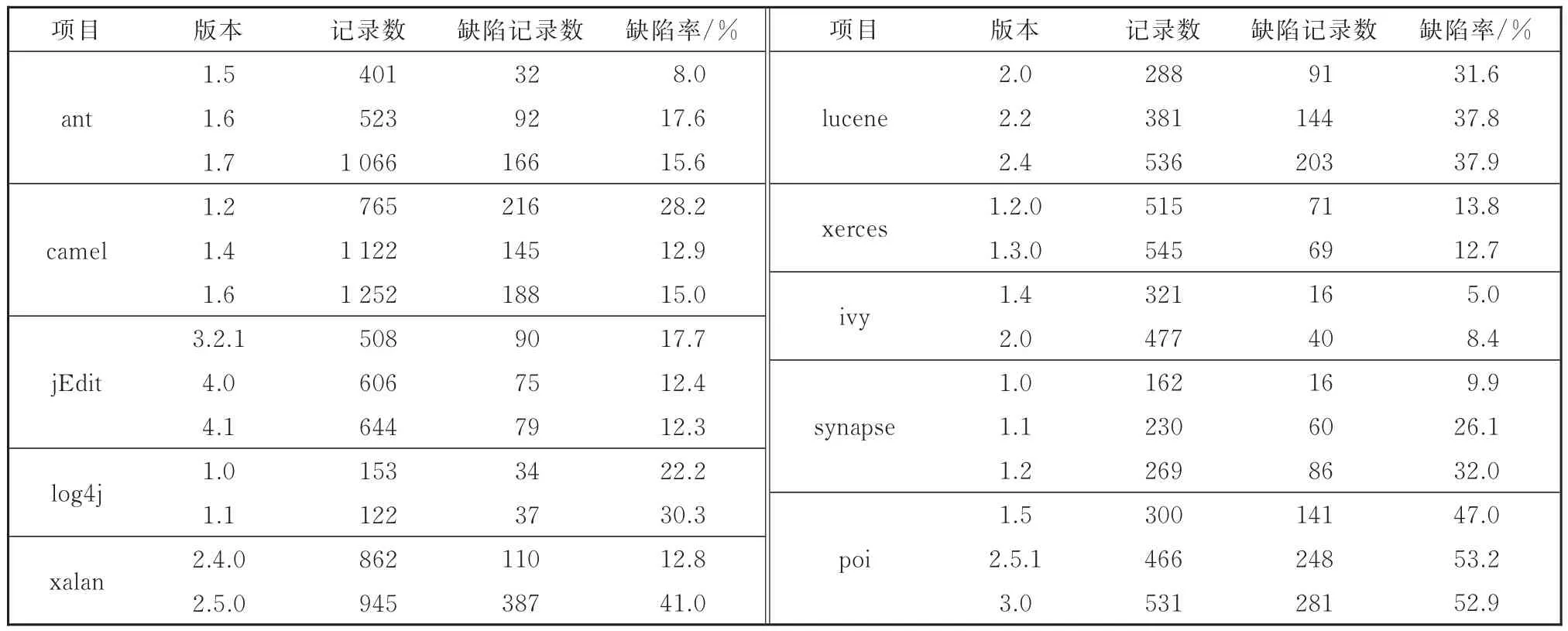
表2 软件缺陷数据集的基本统计信息Table 2 Basic statistics of the defect data set.

2.2 实验设置

本文用F1值度量软件缺陷预测模型的性能。F1值的具体定义如下：

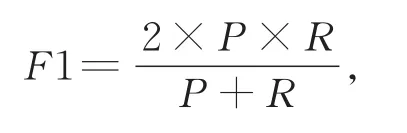
其中，准确率P为预测正确的缺陷模块数在预测为缺陷的模块数中所占比例；召回率R为预测正确的缺陷模块数在原有的缺陷模块数中所占比例。

此外，本文还计算了F1值的后验置信区间（置信度为95%）来度量软件缺陷预测模型的F1值的波动范围，并使用置信区间的长短来衡量软件缺陷预测模型的稳定性。后验置信区间的具体计算公式在文献[19]中给出。

在集成学习模型中，m设置为13。在稳健设计的参数调优中，本文将m设置为3。为了将块正则化m×2交叉验证方法贯串于参数调优和集成学习构建两个阶段，本文首先生成块正则化16×2交叉验证切分，然后将前3组切分用于参数调优阶段，将后13组切分用于软件缺陷预测模型的构建。这种做法可以保证两个阶段中采用的交叉切分间的均衡性，可从整体上有效改善软件缺陷预测模型性能的稳定性。另外，本文所用的支持向量机算法来自R语言的“e1071”程序包的“svm”函数。

2.3 研究问题

本文主要关注如下两点研究问题：

（1）基于稳健优化后的超参数取值是否可以提升跨版本软件缺陷预测模型的F1值的平均性能和稳定性？

（2）基于稳健优化后的超参数取值是否可以提升跨项目软件缺陷预测模型的F1值的平均性能和稳定性？

3 实验结果及分析

针对第2.3节中的两个研究问题，本文分别对跨版本软件缺陷预测任务和跨项目软件缺陷预测任务进行实验。实验结果分别在如下两节中给出。

3.1 跨版本软件缺陷预测模型的实验结果

表3给出了跨版本软件缺陷预测模型的实验结果。从表3中可以得到如下几点结论：

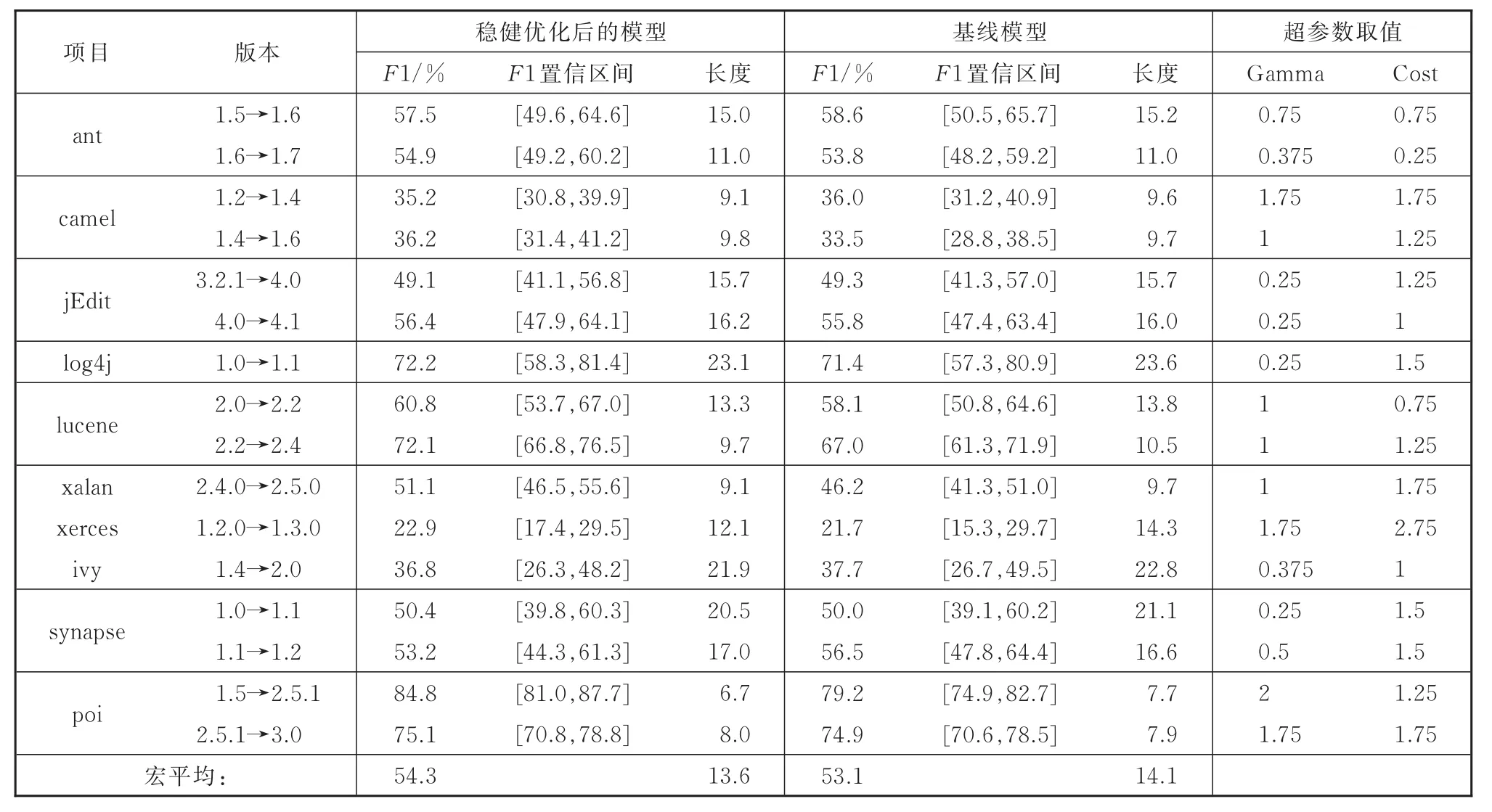
表3 跨版本软件缺陷预测模型的实验结果Table 3 Experimental results of the CVDP task

（1）相比于基线模型，稳健优化后的软件缺陷预测模型的F1值大多数有所上升。总体上讲，稳健优化后的模型宏平均F1值达到了54.3%，相较基线模型的宏平均F1值（53.1%），有1.2%的上升。

（2）从模型的稳定性来看，稳健调优后的置信区间长度（13.6）明显小于基线模型的置信区间长度（14.1）。F1值的置信区间的平均长度可以缩减3.5%。这说明，超参数的稳健优化算法对于模型性能的稳定性上有着明显的影响。

（3）表3的最后两列给出了稳健调优后两个超参数的具体取值。这些超参数明显偏离它们在基线系统中的默认取值。因此，基于稳健调优的超参数选取方法对于改善跨版本软件缺陷预测模型的性能有着明显的积极作用。

（4）根据望大特性信噪比挑选的最优超参数并不完全能达到最高的F1值，比如在跨版本缺陷预测任务lucene 2.2→2.4中，根据望大特性信噪比挑选的最优超参数组合为（Gamma=1，Cost=1.25），而该参数组合的F1值要小于（Gamma=1.25，Cost=1.5）参数组合下的F1值。

3.2 跨项目软件缺陷预测模型的实验结果

跨项目软件缺陷预测模型的实验结果在表4中给出。本节实验中，原项目和目标项目的度量集合相同。因此，本文可以将原项目上构建的软件缺陷预测模型用于预测目标项目的软件模块的缺陷。从表4中，可以获得如下几点结论：

表4 CPDP任务的实验结果Table 4 Experimental results of the CPDP task

（1）稳健调优后的跨项目软件缺陷预测模型的平均性能明显优于基线模型的平均性能。具体地，优化后的模型的宏平均F1值达到49.5%，比基线模型的宏平均F1值（45.4%）高出4.1%。相比于跨版本的软件缺陷预测模型，超参数的稳健调优算法对跨项目软件缺陷预测模型的改进幅度更大。

（2）从F1值置信区间长度来看，稳健调优后的置信区间长度（14.9）明显小于基线模型的置信区间长度（15.3）。其F1值的置信区间的平均长度缩减了2.6%。这个现象和跨版本软件缺陷预测模型的实验结果是一致的。这说明基于稳健调优后的超参数取值可以改善跨项目的软件缺陷预测模型的稳定性。

（3）表4的最后两列给出了超参数Gamma和Cost调优后的具体取值。从最后两列数据可见，这些最优取值均明显偏离基线模型中使用的默认参数值。这说明稳健设计对超参数的优化有着明显的积极影响。

（4）通过比较跨项目软件缺陷预测模型的性能（表4最后一行）和跨版本软件缺陷预测模型的性能（表3最后一行）可见，前者的平均性能明显低于后者的平均性能，并且前者的置信区间长度明显大于后者的置信区间长度。这主要是因为跨项目软件缺陷预测模型中，原项目和目标项目的数据来自于不同的分布。分布间的差异导致了上述现象的发生。尽管如此，基于稳健优化后的超参数仍然可以使两种不同情形的软件缺陷预测模型的平均性能以及稳定性得到明显改善。

综合上述实验结果，基于稳健优化的超参数选择方法可以明显改善软件缺陷预测模型的平均性能和稳定性。