八连杆隔离器的结构及隔冲特性分析

2021-05-17杜志鹏

振动与冲击 2021年9期

张磊，高鹏，闫明，杜志鹏

(1.海军研究院,北京 100161；2.沈阳工业大学机械工程学院,沈阳 110870)

随着精密武器的迅猛发展，水中兵器的爆炸当量和冲击持续时间明显增加，对舰艇结构以及舰载设备的破坏能力越来越强[1]。根据大量实战经验及文献得出，水下非接触爆炸一般不会击穿船体结构，但会使大量舰载设备失效，导致舰艇丧失战斗力[2-4]。在舰载设备中，惯性导航设备是舰艇运行时不可缺少的精密仪器，能够为舰艇提供姿态、速度和位置等信息，当受到冲击损伤后，会严重削弱舰艇的机动和战斗能力，故为保障舰船正常运行，展开对提高惯导设备隔离装置隔冲特性的研究至关重要。

一般隔离装置按缓冲形式可分为主动式和被动式，由于冲击响应属于瞬态运动，而主动式装置需要一定的反应时间，所以被动式隔冲装置应用更为广泛，其中被动式结构主要有钢丝绳、橡胶[5-6]等等，虽然此类结构在进行刚度[7-8]及结构优化研究后具备较好的隔离效果，但不能满足快速和精确复位要求，故国内、外科研人员提出了准零刚度隔离器[9-10]、三向隔离器[11]以及基于Stewart设计理念提出的各种六连杆隔离器[12-15]，使隔离器的抗冲击性能有了显著提高。尽管所提出的结论被广泛的接受和引用，但是诸多研究成果大多是基于速度阶跃法或半正弦波激励得出的时域响应结果，以频域为研究基础，考核其隔振、隔冲性能研究不多。

故基于惯导设备对抗冲击隔离器的要求，同时借鉴多杆结构原理，提出了八连杆抗冲击隔离器，并对该结构进行了静刚度校准、动刚度分析以及隔振性能测试；最终，以大量冲击试验为基础，研究了八杆隔离器在时域和频域上的隔冲性能。

1 主体结构分析及自由度计算

基于Stewart平台设计理念，以及惯导设备的抗冲击防护要求，提出了一种能够防护瞬时冲击的被动式多杆并联隔离器，图1(a)中，该结构主要由隔冲杆、设备安装板、底座、上、下铰链结构以及用于模拟设备的质量块组成。

其中，隔冲杆夹角均为60°的布置方式扩大了结构内部空间范围，可将用于模拟设备的质量体反向安装至隔离器内部，有效的降低了系统体积和设备重心。图1(b)中，8根隔冲杆形成对称结构，使不同隔冲向刚度具有高度的一致性，可将源自任意方向的冲击载荷分解为沿垂、横、纵向的分力，进行缓冲隔离。且为满足隔离器转角精度的要求，将连接隔冲杆、设备安装板和基座的结构设计成具有高精度和高强度特性的球形铰链形式。

同时，如图2所示，由于该结构为多环闭合空间机构，传统计算自由度方法并不适用，故利用螺旋理论[16-17]计算得出，以球铰链作连接元件的隔离器具有6个自由度，进一步验证了结构设计的合理性。

图2 环装闭合结构隔离器Fig.2 Isolator with ring-closed structure

2 刚度及隔振特性分析

2.1 静刚度分析

由于惯导设备隔离器要求能够通过调节弹性元件来实现预紧力的变化，使隔离器具有静态刚度高、动态刚度低的特性。故采用缓冲吸能特性显著的碟簧作为隔冲杆的弹性元件。同时，设定隔离器预紧力为2.5g，即弹性元件发挥作用的临界值，根据式(1)、(2)计算得出，单根杆的垂向负载为51.76 N，轴向负载为59.76 N。

F1=ma/8

(1)

F=F1/cos 30°

(2)

式中:F1为单根杆的垂向负载;F为轴向负载;m为隔离器上层质量;a为冲击加速度。

为保证隔冲杆满足预紧要求，对8根隔冲杆进行了准静态压缩试验。图3中，从单根隔冲杆的静刚度曲线可以得出，其预紧力拐点在60 N附近，与理论计算的轴向负载值比较接近。

图3 单根隔冲杆静刚度曲线Fig.3 Static stiffness curve of single isolator

同时，对隔离器整体结构进行准静态压缩试验，以校核整体结构的准静态静刚度，获得整体结构预紧力拐点为407 N。利用试验数据及式(1)、(2)，得出单根杆垂向负载为50.88 N，轴向负载为58.74 N，与理论计算相符，即该结构满足预紧力设定要求。

2.2 动刚度分析

为了研究八连杆抗冲击隔离器垂向动态刚度变化情况，利用ADAMS对隔离器进行动态刚度仿真，其仿真模型如图4所示。

图4 隔离器垂向动刚度计算Fig.4 The calculation of the vertical dynamic stiffness of the isolator

仿真分析中，固定基座，给动平台施加正弦位移驱动，使其按照正弦规律围绕平台静平衡位置作上下往复运动。位移驱动函数为：0.02sin(2πft)，即位移激励频率为2 Hz、振幅为0.02 m。

结合图5(a)隔冲杆结构，以及图5(b)力-位移曲线，得出隔冲杆内部结构运动过程为：初始阶段，动平台向下运动，使联动杆压缩碟簧组件；到达极限压缩量(位移幅值)后进入阶段2，碟簧向上回弹到达平衡位置后继续运动；在阶段3中，碟簧回弹使联动杆拉动导杆上端向上运动，但在限位结构作用下，碟簧组件上端停止运动，导杆下端继续压缩碟簧；进入阶段4，压缩至极限后向下回弹，周而复始，进行缓冲隔离。

(a) 单根隔冲杆结构

令隔离器的垂向动态等效刚度Ke为

(3)

由式(3)计算得到垂向动态刚度值约为75.17 N/mm。

进一步采用频率为0.5 Hz、2 Hz、6 Hz对隔离器施加激励，以分析不同的激励频率对隔离器垂向动刚度的影响。

如图6所示，一定范围内，随着激励频率的逐渐增加，隔离器的垂向动刚度增大。故为探究在不同频率下的动刚度变化范围，固定激励幅值，设定激励频率范围为0.1～20 Hz，展开大量的垂向动刚度仿真，得出隔离器的垂向等效动刚度值在不同激励频率下的变化规律，如图7所示，在激励频率为6～10 Hz内，隔离器的垂向动刚度较大，但整体垂向动刚度值变化范围不大，约为70～80 N/mm。

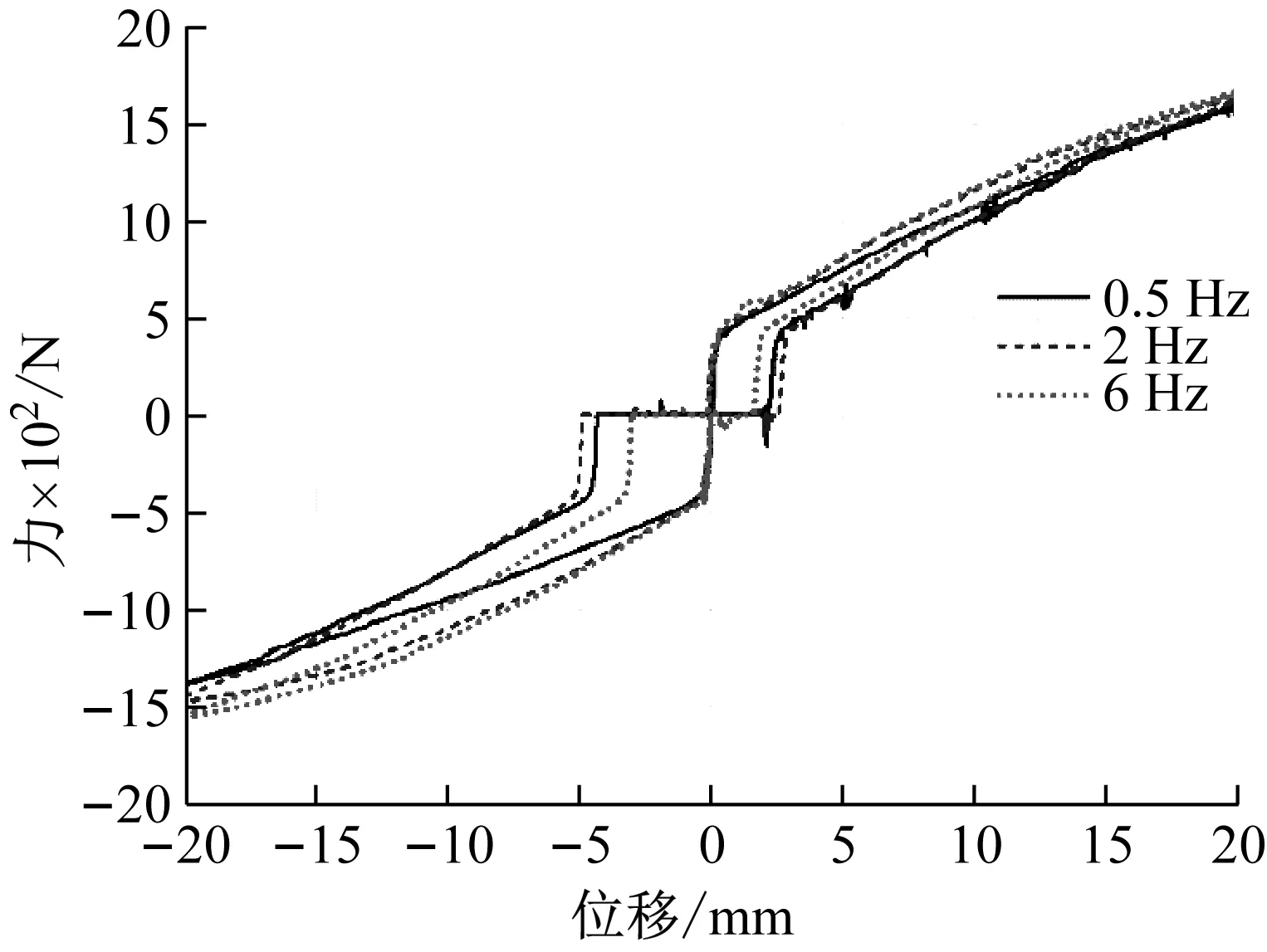
图6 不同激励频率下的垂向动刚度变化曲线Fig.6 Vertical dynamic stiffness curve under different excitation frequencies

图7 垂向等效动刚度变化曲线Fig.7 Vertical equivalent dynamic stiffness curve

同理，采用相同激励方式展开水平向动刚度仿真。得出2 Hz激励频率下，水平向动刚度等效值约为17.03 N/mm。进一步设定频率范围为0.1～20 Hz，仿真发现在3～5 Hz范围内，水平向动刚度较大。

分析垂向、水平向动刚度等效值在不同频率激励下的变化规律可以发现，在激励频率接近隔离器的垂、水平向一阶频率时，该隔离器动刚度最大。

2.3 固有频率及隔振特性

为测量隔离器的固有频率以及隔振性能，对八连杆抗冲击隔离器进行垂向及水平向隔振性能测试。设定扫频范围为5～500 Hz，对振动试验台施加峰值为±51 mm的正弦位移激励信号，同时分别将低频至高频与高频至低频的扫频方式设定为正向及反向扫频，其试验结果如图8所示。

图8 5～500 Hz垂向扫频曲线Fig.8 Vertical frequency sweep curve of 5-500 Hz

从图8中得出，以正、反两种方式进行扫频得到的一、二阶频率以及共振区间、隔振区间范围非常接近，进而推断出，隔离器结构及垂向频率较为稳定，其垂向一阶频率约为10.93 Hz，隔振区间范围为29.7～315.9 Hz及477.9～500 Hz。同理，在相同激励条件下，获得水平向频率约为5.39 Hz，隔离器绕垂向轴旋转45°后频率约为5.37 Hz，隔振区间范围分别约为9.1～500 Hz和9.9～500 Hz。

相比动刚度峰值频率范围，试验获得的固有频率略大，主要原因为八根隔冲杆内部碟簧及垫片数量过多，相互间以及与导杆等零件之间快速接触，产生了过多的库伦摩擦，导致试验值大于仿真值。

3 隔冲特性分析

将采用500 kg正、负双正弦冲击试验机进行垂向及水平向冲击试验，以分析隔离器的抗冲击性能。图9(a)为垂向冲击试验，图9(b)采用倾斜30°的安装模式，将垂向激励转化为沿倾斜方向的载荷，实现水平向冲击。其中，测点1用于测量设备的加速度响应，测点2用于测量台面的冲击加速度。

(a) 垂向

3.1 时域分析

冲击试验中，将结合大量相关冲击试验经验，定制冲击环境主要参数，其中垂向冲击试验的激励加速度最大值为113.12g，水平向冲击为95.59g，正波冲击脉宽分别约为4.9、4.7 ms，负波冲击脉宽分别约为18.6、16.7 ms。

图10加速度响应曲线中，除垂向冲击响应加速度峰值明显衰减外，响应曲线具有最大峰值出现在第二个波峰上的响应特性。主要原因为碟簧可压缩量较大，故在第一次压缩时并没有达到碟簧的压缩极限，而在实际回压中，碟簧压缩量接近相对最大值，所以正向最大峰值出现在第二个波峰上。

图10 垂向冲击及设备加速度响应Fig.10 Vertical impact and acceleration response of equipment

将试验的冲击数据作为激励，对隔离器进行冲击仿真，并与试验进行对比。同时，提取冲击仿真中相同时间节点处碟簧的变形量及加速度响应，如图11所示，在垂向加速度最大响应位置处，碟簧变形最大，验证了上述分析的正确性。

图11 垂向冲击中的碟簧变形量Fig.11 Deformable amount of disc spring in vertical impact

在图12的水平向冲击试验及仿真响应结果的对比中发现，该曲线并没有体现出与垂向冲击结果类似的响应特性，响应的第二个正向峰值并不是加速度响应的最大值。

图12 水平向试验及仿真响应结果对比Fig.12 Comparison of the results of horizontal test and simulation response

分析图13中隔冲杆布置及碟簧变形量得出，在水平向冲击试验中，由于为倾斜安装，隔冲杆受力并不完全相同，不同隔冲杆变形量差异较大，所以没有垂向冲击响应的明显的峰值响应特性。即峰值响应结果特性与结构形式有关，安装角度变化会产生非均匀受载现象，进而影响响应峰值分布。

(a) 水平向隔冲杆布置图

为更系统的研究八连杆抗冲击隔离器在时域上的抗冲击性能，逐级施加冲击载荷，展开多工况冲击试验，并与仿真的正向加速度响应幅值进行对比分析，见表1、表2。

表1 垂向加速度响应对比Tab.1 Comparison of vertical acceleration responses

表2 水平向加速度响应对比Tab.2 Comparison of lateral acceleration responses

如表1、2所示，垂向及水平向仿真和试验响应结果基本吻合，误差在5%左右，验证了仿真的准确性。基于表1、2加速度冲击、响应峰值数据以及隔离率计算公式[18]，得出垂向隔离率达到80%以上，水平向隔离率最高接近90%，这是由于水平向刚度软特性[19-20]相对明显，导致其隔冲效果优于垂向。同时发现，冲击载荷越大，隔冲效果愈显著，说明时域上，该隔离器的隔冲能力满足抗冲击要求。

3.2 频域分析

一般地，由于实际冲击环境较为复杂，仅从时域上进行分析，难以给出令人信服的隔冲效能判据，故需要对隔离器在频域上展开隔冲性能研究。利用所编制的MATLAB程序，以冲击试验垂向加速度113.12g、水平向95.59g及试验、仿真响应数据为基础，绘制冲击响应对比谱。

从垂向对比图谱14中发现，谱位移约为0.02 m，同样在台面最大位移处，表明了此图谱的准确性。在低频段，响应谱速度最大值在系统一阶固有频率处，且大于冲击谱速度值，也就是说设备的速度响应被放大，随后衰减，在20 Hz之后响应谱速度小于冲击值。在中、高频段仿真与试验的谱加速度较为接近，在10～20g，即谱加速度有明显的衰减。

与图14相似，图15的水平向对比谱中，低频段谱速度最大值接近系统水平向一阶固有频率，随后衰减，且小于冲击谱速度值。在谱加速度方面，仿真与试验的谱加速度值比较接近，均在10～20g，衰减明显。