基于HRV非线性特征的心律不齐自动分析

郭景诗，乔晓艳

(山西大学 物理电子工程学院，山西 太原 030006)

心律失常是引起各种心脏病患者猝死的主要原因之一，也是近年来心血管领域十分活跃的研究内容. 由心脏病变而引起心脏跳动时间间隔异常的现象称为心律不齐，是心律失常的表现之一，心律不齐情况严重的话会危及人的性命，所以其诊断在临床医学中十分重要[1]. 心电(ECG)信号相邻心拍中R-R间期的变化称为心率变异性(HRV)，其形态特征可以反映潜在的心律不齐病症，在临床诊断中有很重要的研究价值[2]. Diptangshu Pandit等[3]采用基于实时滑动窗口的最大最小差分算法来定位ECG信号的QRS波群，进而得到HRV信号，具有较高的准确性，但是计算时间成本高、 鲁棒性差； Tanushree Sharma等[4]提出了一种基于加权全变差去噪的QRS波检测方法，可以有效地抑制QRS波的频谱重叠，但波形检测准确性差，不便于实际应用； Santanu Sahoo等[5]提出多分辨率方法检测心电信号QRS波并提取心率变异性，该方法具有较好的检测性能和较低的错误率.

国内外对HRV信号的时域、 频域分析较多，对其非线性分析的研究却较少，且有效性尚需提高. 比如Mohit Kumar等[6]通过提取HRV信号的K近邻熵和模糊熵，实现对冠状动脉疾病的自动诊断，但准确率并不高. 由于HRV信号是非线性的，对其进行非线性分析十分必要.

目前，通常采用阈值检测法来提取HRV特征信号，但是鉴于不同个体或者同一个体在不同时刻的ECG信号幅度存在差异，通过直接设置阈值来检测信号会存在一定的偏差[7]，对R波检测的准确性较差，导致HRV特征信号误差大，进而影响HRV的非线性分析. 本文采用小波变换方法，通过小波分解提取小波系数模极大极小值和过零点，充分利用小波变换对突变点检测的有效性和准确性，实现对心电R波的定位和对HRV信号的精准提取，从而保证了HRV非线性分析的准确性. 由于HRV非线性特征提取与分析最终是为了实现机器自动诊断，因此，在统计分析HRV非线性特征基础上，旨在寻找到差异最显著的非线性特征，试图用尽量少的非线性特征达到对心律不齐疾病的机器有效诊断.

1 MIT数据库

美国的MIT ECG数据库是当前世界上被普遍采用的数据库之一，它由很多子库组成，每个子库中存有某种特定类型的ECG数据，其中最常被采用的是MIT-BITArrhythmia数据库和MIT-BIT QT数据库[8]. 本文采用的数据来源于MIT-BITArrhythmia数据库，其中一共包含48条数据，每条时长30 min左右，采样率是360 Hz，每一条数据至少包括3种文件： 头文件——存储方式为码文字； 数据文件——采用212格式存储，即每3个字节存储两个数据，每个数据2 bit； 注释文件(.atr, .al, .aiM等)——主要采用MIT(占用2 B 存储空间)和AHA(占用16 B存储空间)存储格式. 论文分别读取30段时长为2 min的正常心电和心律不齐心电数据，通过字节移位操作将心电数据由二值数据转换为十进制数据.

2 小波变换

2.1 小波变换检测信号突变点

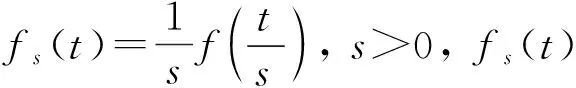
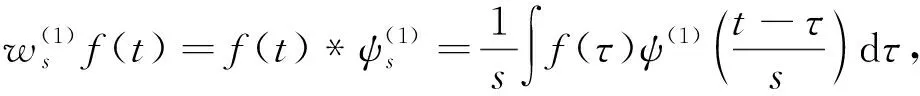
(1)

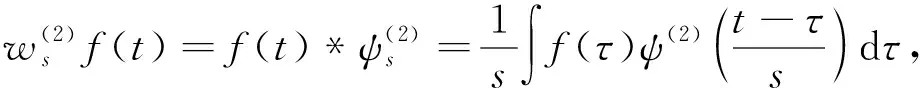
(2)

式中：ψ(1)(t)和ψ(2)(t)分别为θ(t)的一阶导数和二阶导数，也称作小波母函数，则

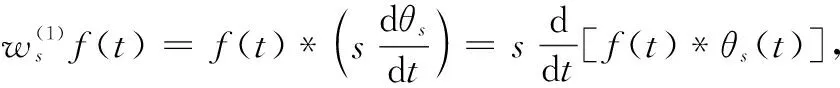
(3)

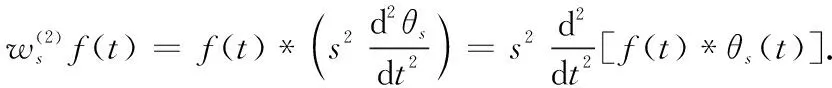
(4)

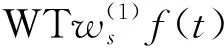
2.2 小波熵

小波熵(Wavelet Entropy，WE)是结合WT与信息熵理论的一种非线性特征分析方法. 对于确定性信号，WE为零； 对于复杂的随机信号，WE较大. 获取WE的过程为

1) 对于信号x(t) ，其WT为

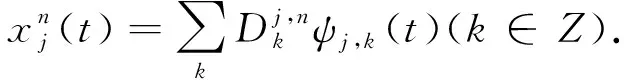
(5)

2) 信号重构为

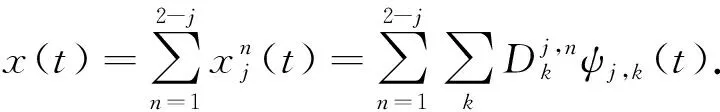
(6)

3) 子小波的能量谱

4) 由此得到信号的小波总能量

5) 小波能量分布表示为

6) 计算WE为

WEm(P)=-∑Pnln(Pn).

3 心电R波检测与HRV特征信号提取

3.1 心电信号预处理

ECG信号频率低且非常微弱，一般地，其幅值在5 mV以下，其频率范围为0.05 Hz～100 Hz，受周围环境和人工测量的影响，ECG信号通常存在3种干扰类型： 肌电(EMG)干扰、 基线漂移和工频干扰[10]. MIT数据库中的数据已滤除工频干扰，结合本研究只需提取心电R波的实际情况，本文仅进行滤除EMG干扰的预处理.

由于EMG信号的主要频带范围为100 Hz～300 Hz，论文选取Butterworth低通滤波器来滤除EMG信号[11]. 图1 所示是过滤ECG干扰前、 后的ECG信号，可以看出高频的EMG干扰得到有效滤除.

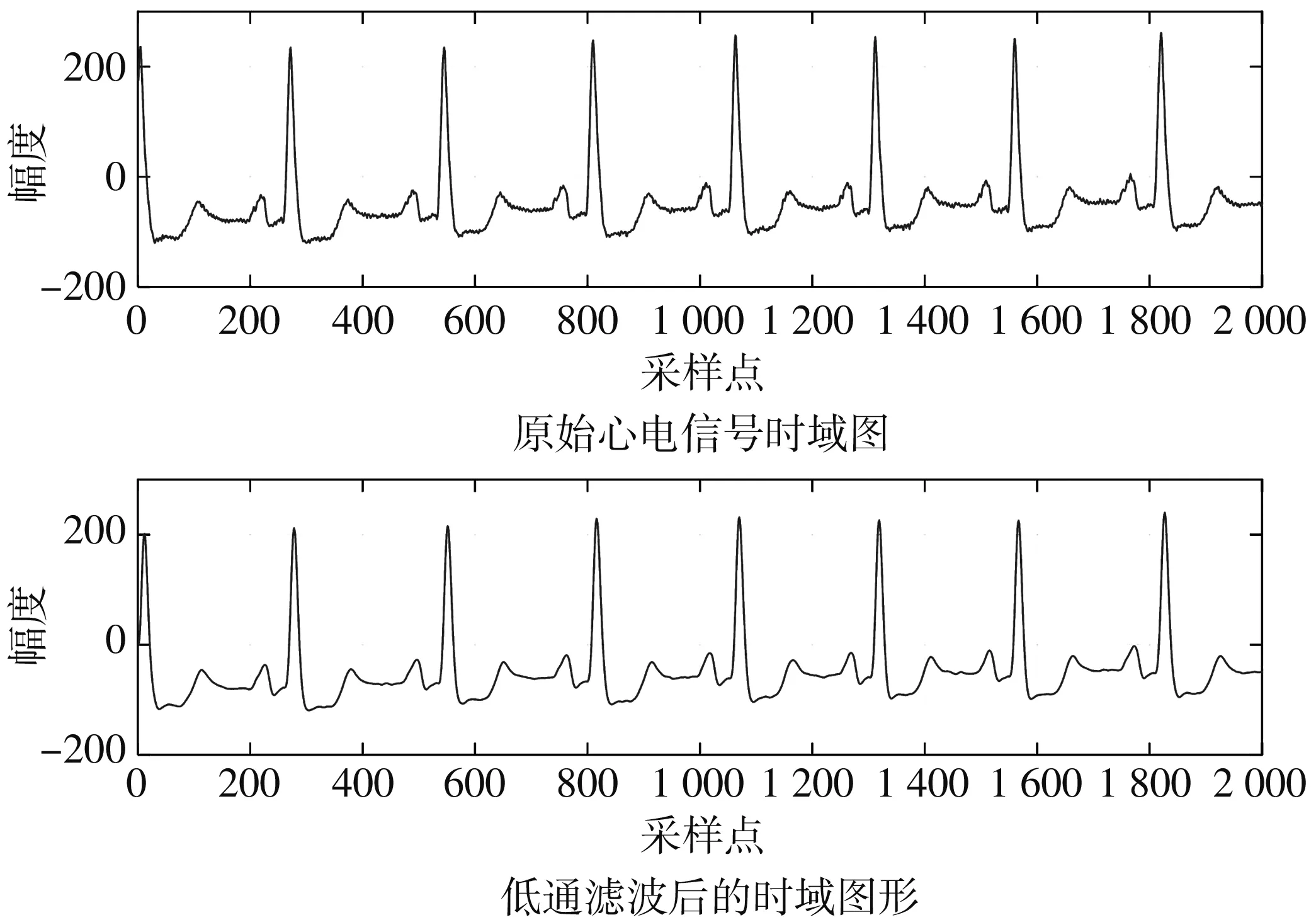
图1 原始ECG信号和滤除肌电干扰后的ECG信号图Fig.1 Original ECG signal and ECG signal after filteringEMG interference

3.2 基于小波变换的R波检测

图2 是一段典型的ECG信号波形，主要由P波、 T波和QRS波群构成.

提取HRV信号首先需要提取ECG信号的 R波，基于WT的时频定位分析能力和多分辨率的特点，可以将其应用于ECG信号QRS复合波的定位分析当中. 根据前述WT检测信号突变点的方法，选取与ECG信号形态近似的mexh小波作为小波母函数，以提取ECG信号的波，具体算法过程为：

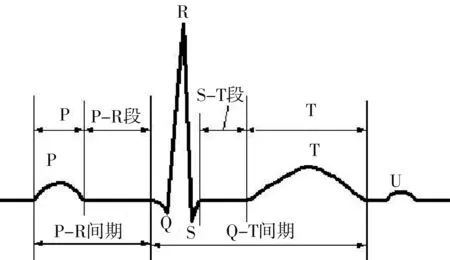
图2 心电图波形Fig.2 ECG waveform

1) 确定WT系数： 将预处理后的ECG信号进行6层mexh小波分解，得到WT系数矩阵wsig.

2) 检测极大极小值对： 在小波变换域上，首先找到所有峰值点并放入矩阵中； 将矩阵中的数据进行排序，获得前8个极大值点和后50个极小值点的两个均值后，以两者之间差值的25%～55%(根据不同数据幅值的差异来进行灵活调整)作为阈值来检测整条数据的极大极小值点来获得极大极小值对(Max-Min Pairs)[9].

3) 初步确定R波峰值点： 求取Max-Min Pairs的零交叉点，记此点的位置点为rvalue(i)，初步确定rvalue(i)是R波峰值点，以此类推求取整条ECG数据的R波波峰.

4) 排除误检漏检： 计算相邻极值点之间的时间间隔Rt，若Rt小于200 ms或大于400 ms，则删掉幅值较小的一个以获取新的R波峰值点矩阵rvalue.

5) 对原始信号进行精确校准： 在rvalue(i)之前和之后取5个采样点，在这10个采样点中找到最大值，并将该点重新确定为R波的峰值.

由此提取得到的心电R波波峰(图中·所示)如图3 所示.

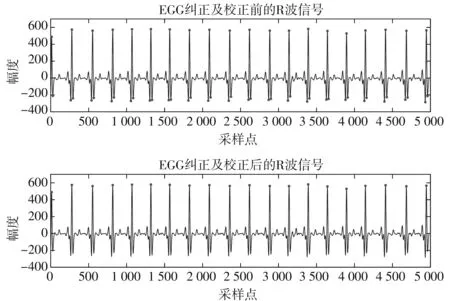
图3 小波变换提取的R波波峰Fig.3 R wave peak extracted by wavelet transform

3.3 HRV特征信号提取

HRV信号是用来形容心脏在每个跳动节拍内存在的微小变化现象的，是ECG自动分析诊断的重点之一[12]. 通过R波波峰的一阶差分计算，可以得到HRV特征信号. 图4 和图5 分别为提取的正常心律心电和心律不齐心电的HRV信号时域图.

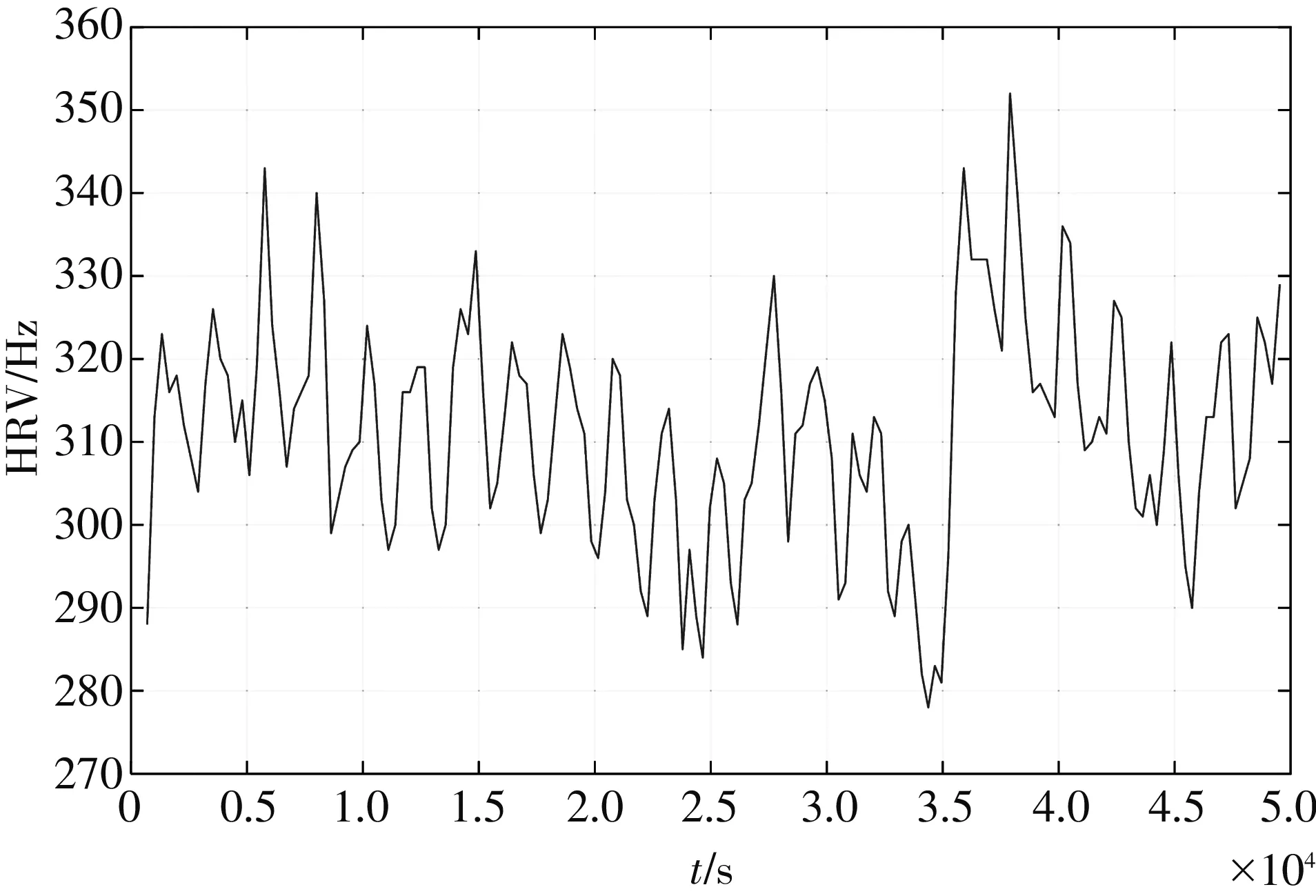
图4 正常心律HRV信号波形图Fig.4 Normal heart rhythm HRV signal waveform

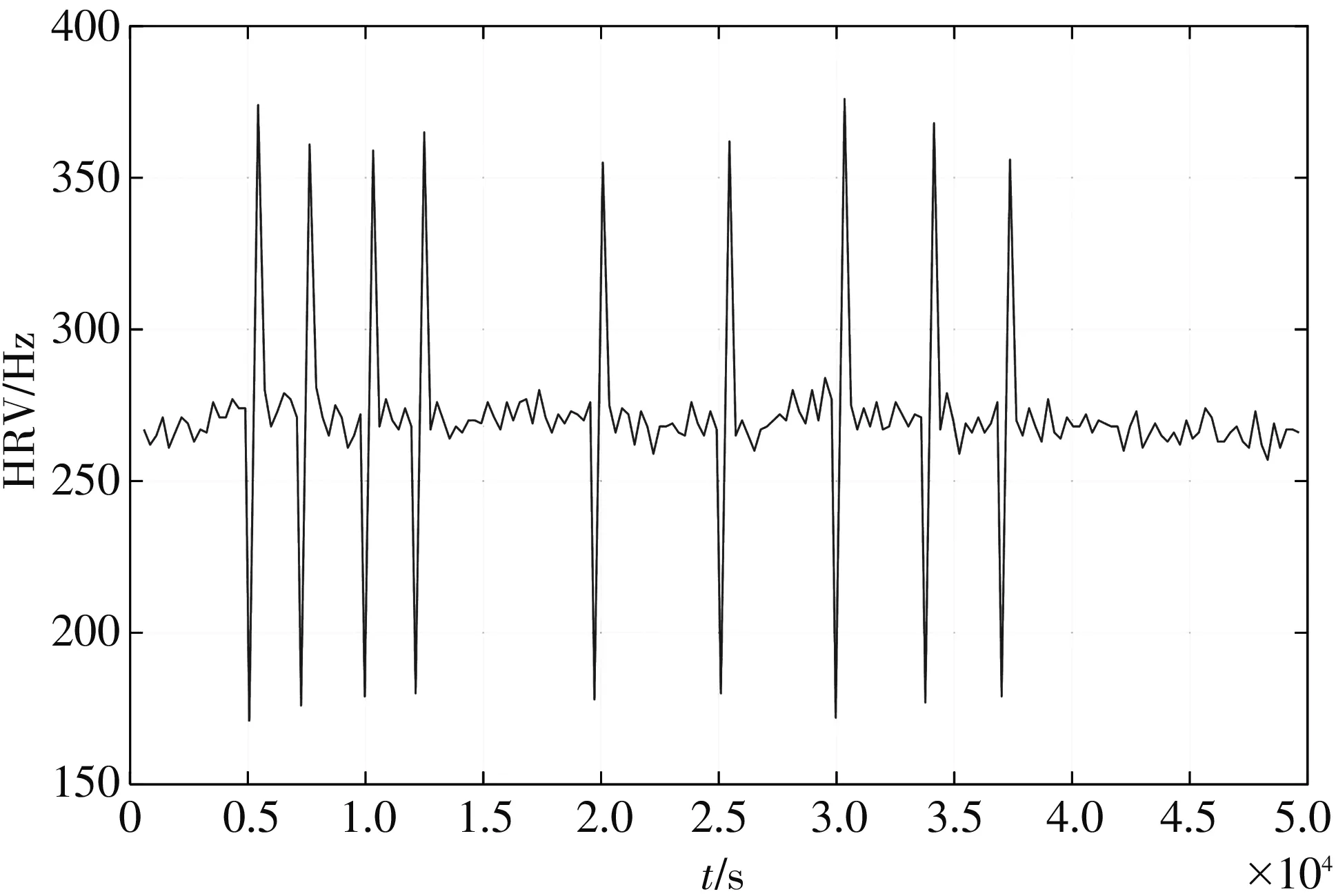
图5 心律不齐HRV信号波形图Fig.5 NHRV signal waveform of arrhythmia

由图4 和图5 HRV信号可以看出，正常心率和心律不齐的HRV信号均呈现非线性变化. 正常心律的HRV变化不大、 较规则，而心律不齐的HRV起伏变化较大，且随一定的时间间隔发生跳动. 由此可见两种情况的HRV信号存在明显的差异，临床诊断时可通过分析HRV信号的各种特征来判断患者是否存在心律不齐.

4 HRV信号的非线性分析

在获得HRV信号后，通过提取HRV信号的WE、 近似熵(Approximate Entropy，ApEn)、 基本尺度熵(Basic-Scale Entropy，BsEn)3种非线性特征来进一步分析正常心率和心律不齐两种情况下的HRV特征差异.

4.1 小波熵

WE是一种把小波分解多尺度优势和信息熵不确定性相结合的特征分析法，可以反映多频信号的复杂性并获得信号的非线性特征信息. 论文提取了正常和心律不齐两种情况下各30条HRV信号的小波熵，进行归一化后，得到散点图，如图6 所示，进行差异性统计分析，单因素方差分析结果如表1 所示.

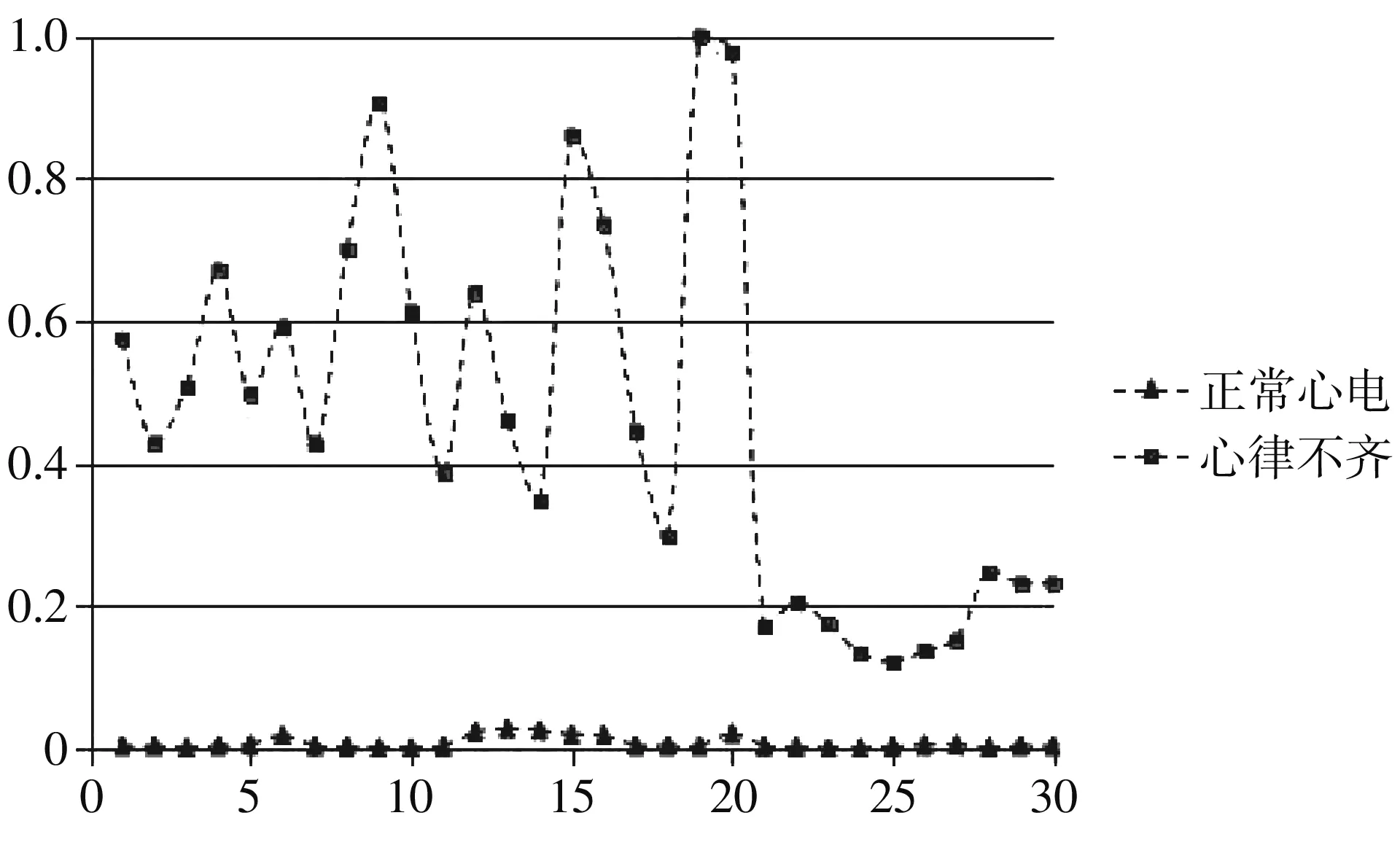
图6 两种HRV信号的小波熵散点图Fig.6 Wavelet entropy scatter diagram of two HRV signals

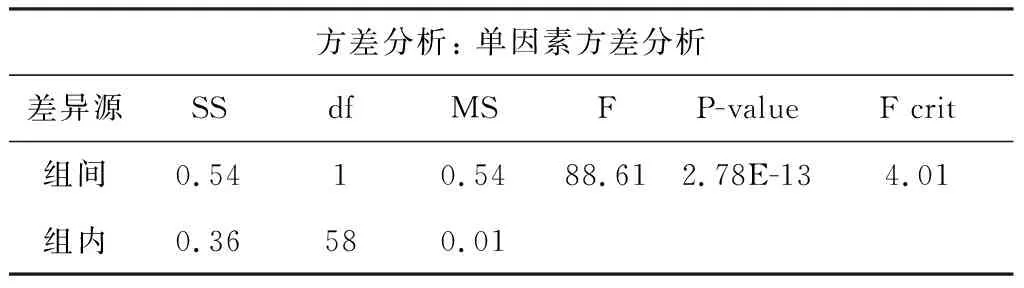
表1 小波熵方差分析Tab.1 Wavelet entropy analysis of variance

从图6 可以看出，心律不齐HRV信号的小波熵大于正常HRV信号的小波熵，并且变化更为显着，表明心律不齐HRV信号更加混乱和复杂.

从差异性分析结果可以看出，P-value<0.01，表明两种情况的HRV小波熵值有显著性差异.

4.2 相空间重构

提取HRV信号的非线性特征参数，首先是将HRV信号视为一维时间序列[x(1),x(2),…,x(N)]，然后将其映射到高维空间以实现相空间重构[13]. 本文使用C-C法，由Kim在年提出，用时间延迟τ构造m维相空间向量，以实现一维HRV时间序列的重构，重构后的信号为

Xi=[X(i),x(i+τ),…,x(i+(m-1)τ)],

(7)

式中：i=1，2，…，N-(m-1)τ；τ为延迟时间；m为嵌入维数.

4.3 近似熵

ApEn是描述复杂度和不确定性的非线性动态参数. ApEn的值越大代表时间序列越杂乱； 正有界的ApEn代表时间序列或系统是混沌的[14]. 在实际情形中，可运用较少的数据量对估算出相对稳定的ApEn值，具体过程如下：

1) 重构长度为N的时间序列[x(1),x(2),…,x(N)]，以便在m维相空间中获得Y(i)=[x(i),x(i+1),…,x(i+m-1)]与Y(j)=[x(j),x(j+1),…,x(j+m-1)]，其中i,j=1,2,N-m+1；

2) 定义Y(i)与Y(j)之间的距离d[Y(i),Y(j)]为两者对应元素中差值最大的一个

d[Y(i),Y(j)]=

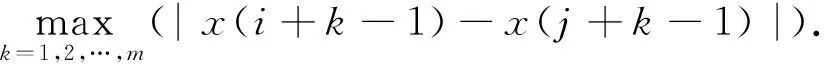
(8)

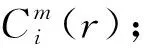
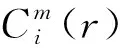
(9)

5) 设定嵌入维数为m+1 ，重复步骤1)～4)，得到Φm+1(r)；

6) 计算ApEn为： ApEn(m,r,N)=Φm(r)-Φm+1(r).

本文选择的嵌入维数为2，距离为0.15倍的一维时间序列差，提取了30对HRV信号的近似熵，归一化后画出散点图如图7 所示，差异性分析结果如表2 所示.

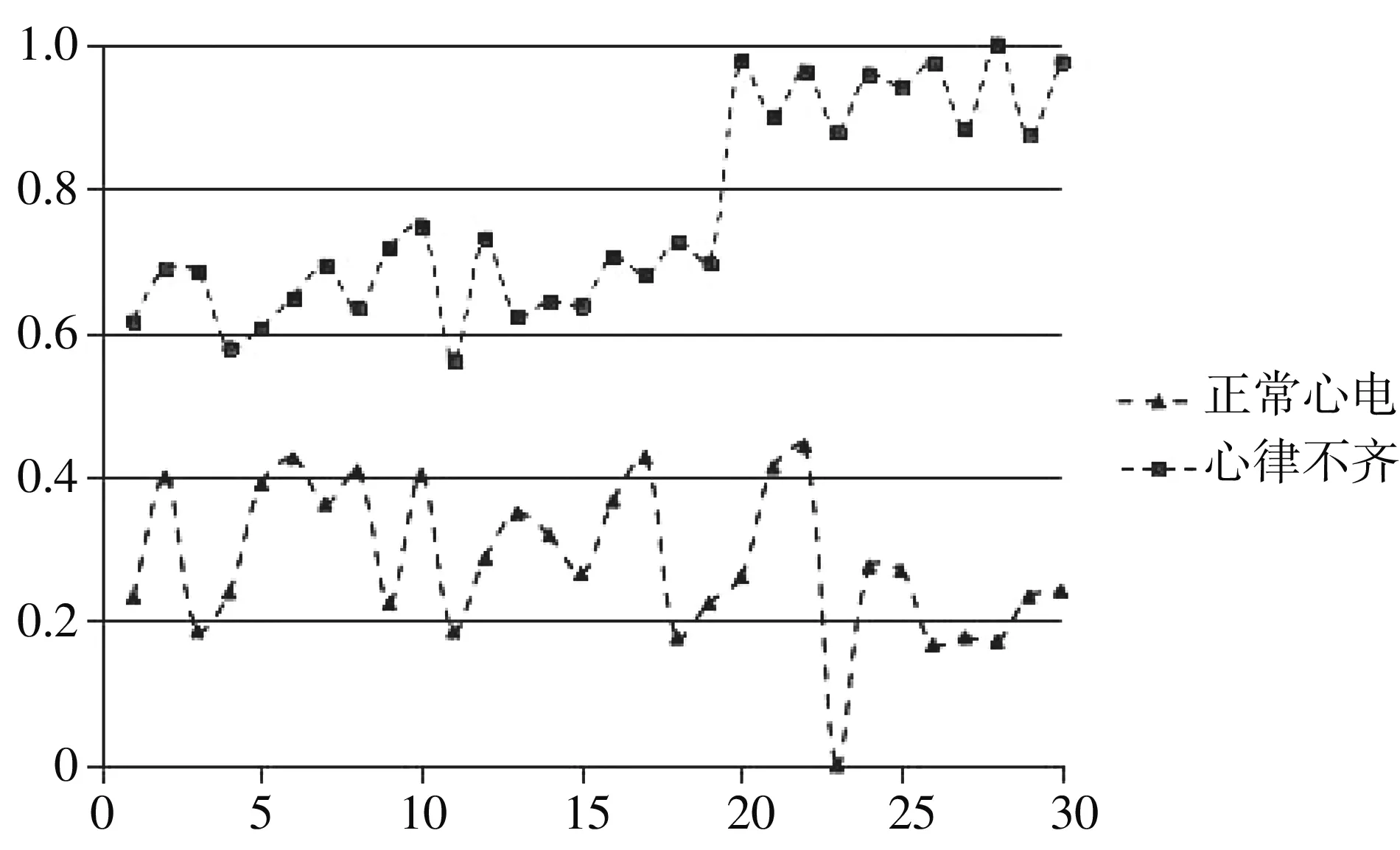
图7 两种HRV信号的近似熵散点图Fig.7 Approximate entropy scatter diagram of two HRV sign

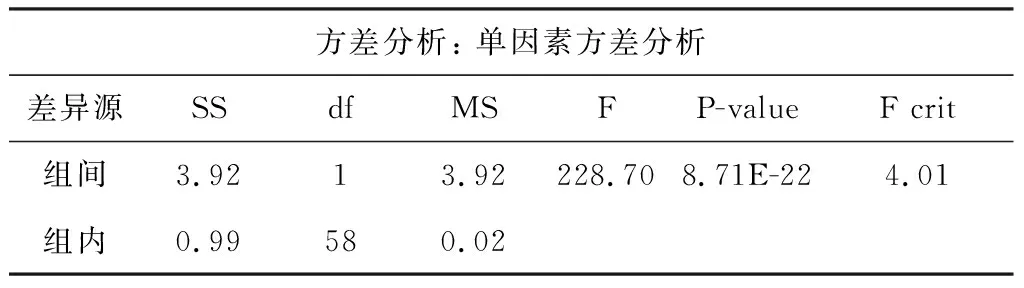
表2 近似熵方差分析Tab.2 Approximate entropy analysis of variance

从图7 可以看出，正常和心律不齐两种情况下的ApEn都为正值，说明都为混沌信号； 而心律不齐的HRV信号ApEn要大于正常心律HRV信号的ApEn，表明心律不齐的HRV信号更加混乱，混沌性更强.

从差异性分析可知，P-value<0.01，表明两种情况的HRV信号的近似熵差异性显著，可用来区分正常心律和心律不齐心电信号.

4.4 基本尺度熵

2005年，李锦等[15]提出基本尺度熵(BsEn)法研究HRV信号，与传统的静态划分符号方法不同，BsEn采用动态自适应划分符号，利用相空间m维矢量的BsEn随时间的变化，自适应地去选择划分符号的标准，方法简单、 运算快速. BsEn描述了时间序列复杂性，其值越大，序列的无序性越大. 本文采用文献[15]的方法，分别选取嵌入维数m=3，4，5，6，7仿真计算HRV基本尺度熵并进行单因素方差分析，结果显示： 当嵌入维数m=3时，HRV基本尺度熵对正常心电和心律不齐心无显著性差异； 而当嵌入维数m>3时，基本尺度熵特征对正常心电和心律不齐心电显示出了统计学显著差异，P值小于0.01，故设置嵌入维数m=4，提取HRV的基本尺度熵，归一化之后画出散点图如图8 所示，差异性分析结果如表3 所示.

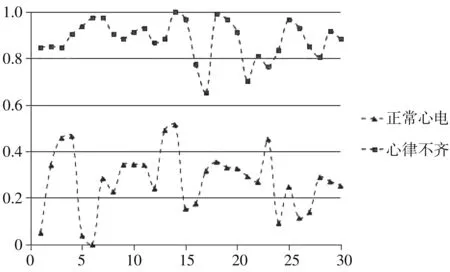
图8 两种HRV信号的基本尺度熵散点图Fig.8 Basic scale entropy scatter diagram of two HRV signals

表3 基本尺度熵方差分析Tab.3 Basic scale entropy analysis of variance

从图8 可以看出，BsEn特征对正常人和心律失常患者均表现出较强的非线性复杂度； 心律不齐HRV信号的BsEn要大于正常心律HRV信号的BsEn，表明心律不齐HRV序列更复杂，无序性更大，混沌性更强.

从差异性分析可知，P-value<0.01，表明两种情况的HRV信号的基本尺度熵差异性显著，可用来区分正常心律和心律不齐心电信号.

5 结 语

本文采用小波变换检测奇异点的方法，通过提取ECG信号的模极值点和过零点，定位R波并计算其波峰的一阶差分，得到HRV特征信号. 采用C-C法对HRV序列进行相空间重构，提取近似熵、 基本尺度熵和小波熵3种特征，实现正常心律和心律不齐患者HRV特征信号的非线性分析. 结果表明，心律不齐HRV信号的混沌性较强，无序性和复杂性较大，小波熵、 近似熵和基本尺度熵皆可用来分析诊断心律不齐.