高动态北斗B1I信号的快速捕获算法研究

郭 维，韩跃平，耿 璇

(中北大学 信息与通信工程学院，山西 太原 030051)

北斗卫星导航系统是中国自主建设、 独立运行的卫星导航系统，为全球用户提供全天候、 全天时、 高精度的定位、 导航和授时服务. 实现定位、 导航和授时功能的前提是捕获及跟踪卫星信号，而它的第一步是捕获信号，即获得卫星信号的码相位与载波频率. 由高动态造成的多普勒频移导致用户接收机接收到的信号的频率与码相位均发生了改变，因此，对在较短时间内较为准确地捕获到卫星提出了更高的要求.

目前，常用的卫星捕获算法主要有时域串行捕获算法、 匹配滤波器算法、 基于FFT的并行码相位捕获算法等. 20世纪末，文献[1]首先将匹配滤波器引入卫星捕获算法，接着将FFT用于捕获算法； 随后，C/A码的捕获开始采用基于FFT的循环相关捕获算法[2]，极大地提高了捕获速度； G.J.R.Povey 等人在文献[3]中首次提出了将匹配滤波器与FFT结合起来进行快速捕获，其在部分匹配滤波器的基础上加入了FFT运算，在较大多普勒频移的条件下提高了检测概率并减少了捕获时间； 此后，Kong S在文献[4]中正式提出了PMF-FFT算法. PMF-FFT算法是将匹配滤波器分成 P段部分匹配滤波器，使得伪随机码部分可以快速地进行匹配运算，极大地减少了码相位求解的时间，然后将每段匹配滤波器的输出相干累加求和，之后再进行FFT，选择出最大值进行捕获确定[5].

时域串行捕获算法是按照一定的步长依次搜索码相位和载波频率，缺点是捕获时间较长，只适用于对于捕获速度要求不高的环境，不适用于高动态环境[6]. 在捕获到码相位的同时得到了多普勒频移，极大地增加了捕获效率，但同时也增加了算法的实现复杂度，并带来扇贝损失，降低了检测概率. 因此，本文提出了改进的PMF-FFT算法，将经过部分匹配滤波器的输出求和之后加窗函数，来减小FFT带来的扇贝损失.

1 传统捕获算法

传统的北斗卫星信号快速捕获算法主要分为两种，一种是在时域上的串行捕获算法，另一种是基于快速傅里叶变换的快速捕获算法.

时域上的串行捕获算法是在确定了频率范围和码相位范围后，以一定的频率步长和码相位步长依次对不同卫星进行二维搜索，直到出现相关峰值则认为捕获成功. 图1 为串行捕获算法的原理图，由图1 可知，串行捕获算法的结构主要由本地振荡器、 伪码发生器、 乘法器、 积分器等模块组成. 经过下变频等处理后的接收信号首先与本地载波同向及正交分量分别相乘，得到I，Q两条支路信号，然后均与本地伪码进行相关运算，I，Q两条支路经过积分器后的输出结果相加后求模，将结果与门限值比较，高于门限值时捕获成功，否则按照一定的步长改变频率后继续之前的过程； 若未捕获成功，按照一定的步长改变伪码相位进行计算，如果依然没有捕获成功，则改变卫星号继续之前的过程，直至捕获成功[7].

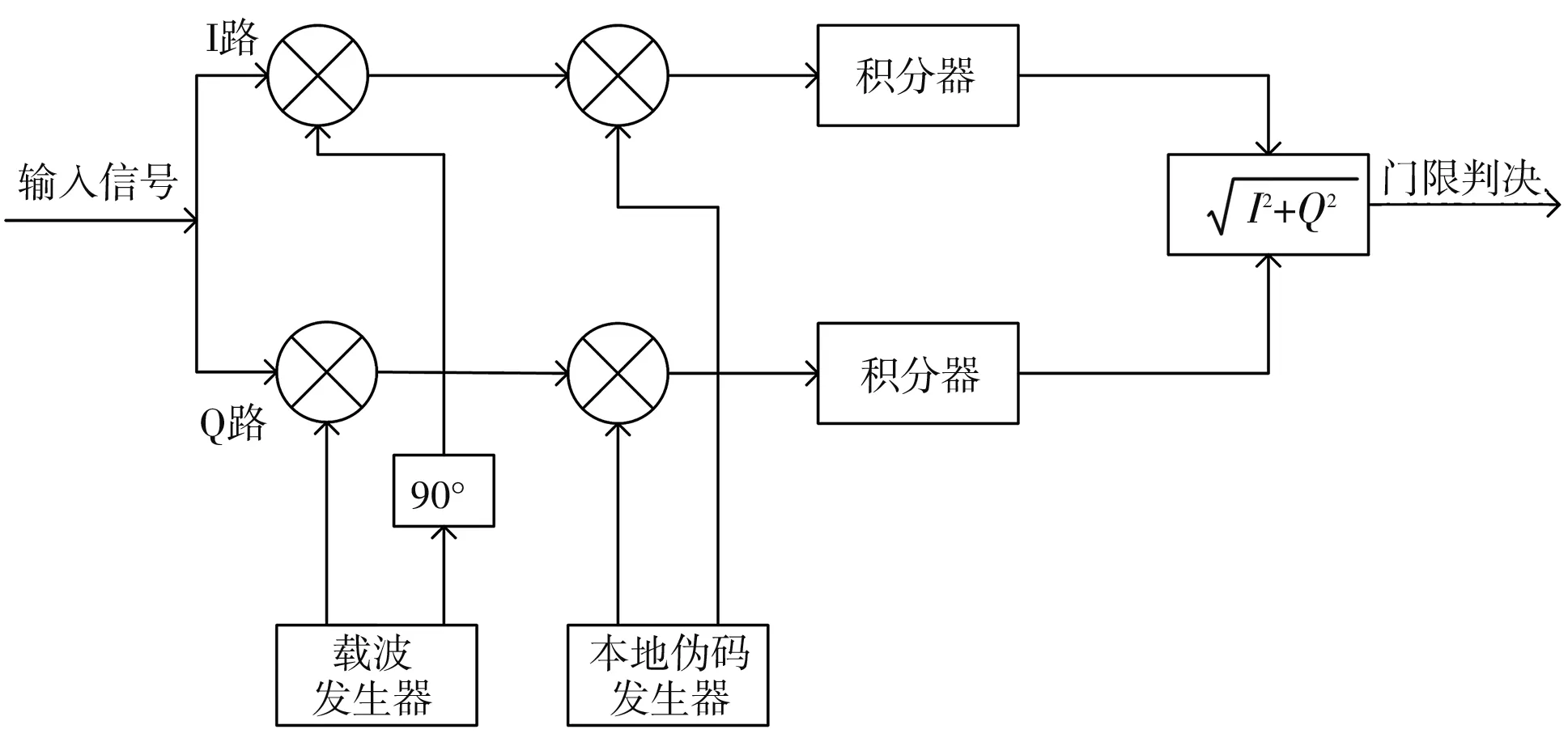
图1 串行捕获算法原理图Fig.1 Schematic diagram of the serial capture algorithm

基于快速傅里叶变换的快速捕获算法是利用快速傅里叶变换将时域的相关卷积运算转换为频域的乘法运算，实现原理如图2 所示，首先下变频信号与本地载波同向及正交分量相乘，得到I，Q两条支路信号并进行FFT变换，然后将变换的结果与本地伪码的FFT变换后的结果进行相乘，最后将进行了IFFT变换的结果与门限值比较，如果超过门限值则捕获成功，否则调整本地载波与伪码的值并重复之前的过程，直到捕获成功[8-10].

虽然串行捕获算法实现起来简单，但是运算繁琐，消耗时间较长； 虽然基于快速傅里叶变换的算法捕获速度快，但是运算量很大. 因此，采用改进的PMF-FFT来解决问题，可以更快地完成信号的捕获.

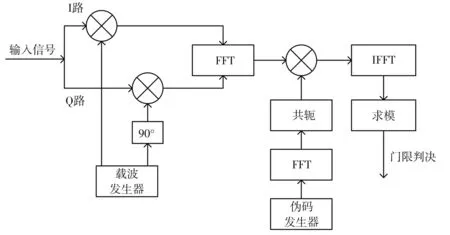
图2 基于FFT的快速捕获算法原理图Fig.2 Schematic diagram of fast acquisition algorithmbased on FFT

2 改进的PMF-FFT算法

匹配滤波器是最佳线性滤波器，是一个计算输入信号自相关函数的相关器[11]. 输入信号经过匹配滤波器的输出结果信噪比最大，图3 为匹配滤波器系统框图.

图3 匹配滤波器原理图Fig.3 Schematic diagram of matched filter

输入信号为

X(t)=s(t)+n(t),

(1)

式中：s(t)为输入信号；n(t)为功率谱密度是n0/2的高斯白噪声，系统冲击响应为h(t)，频率响应为H(ω).

输入信号和输出信号的频谱函数分别为

(2)

so(ω)=S(ω)H(ω).

(3)

通过滤波器后的输出信号为

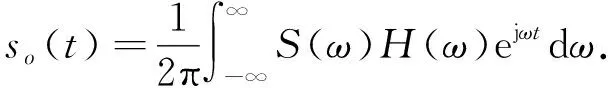
(4)

当信号通过匹配滤波器的输出信噪比SNR最大时，系统函数为

H(ω)=kS*(ω)e-jωt0,

(5)

h(t)=ks*(t0-t),

(6)

式中：k=1，输出信号为

s0(t)=s(t)*h(t)=kR(t-t0).

(7)

由式(7)可知，匹配滤波器的输出波形是输入波形自相关函数的k倍，所以匹配滤波器可以看成是一个计算输入信号自相关函数的相关器[11]，下变频后的信号被送入寄存器中，另外存在对应的寄存器，该寄存器存放有某一相位的伪码序列. 每送入一个信号，对应的两路寄存器进行一次相乘运算并将结果相加，相当于完成一次相关运算[12，13].

PMF-FFT算法中含有P个X级部分匹配滤波器，每个部分匹配滤波器依次时延X，即XP=M，其中，M为伪码的相位范围. 第一个部分匹配滤波器与前X个码片进行匹配相关运算，第二个处理下X个码片，依次进行处理； 然后将这些输出结果直接送入一个N点FFT进行补偿运算，将输出的结果与门限值比较，完成多普勒频移的估计[14]，图4 为PMF-FFT算法原理图.

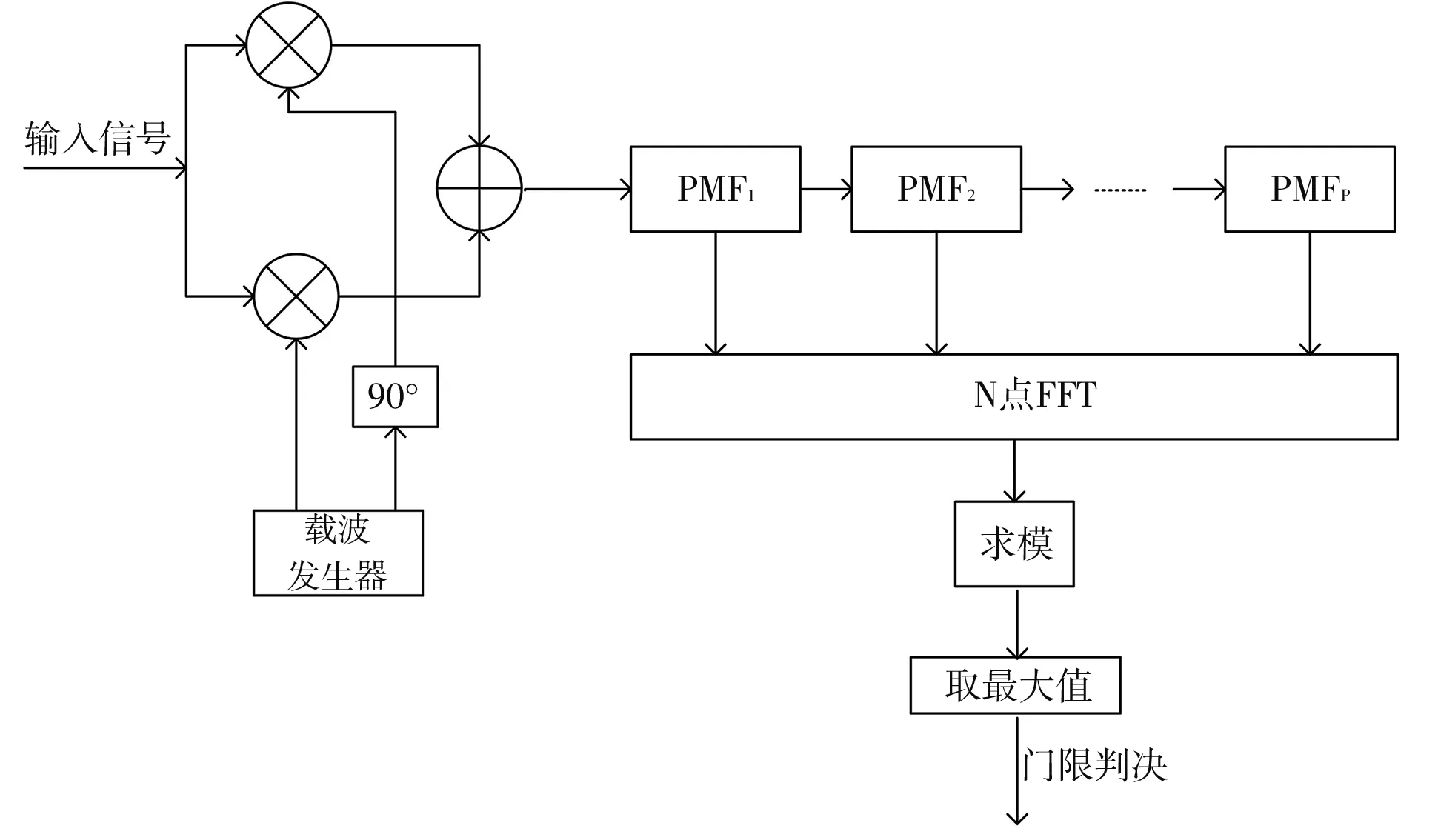
图4 PMF-FFT算法原理图Fig.4 Schematic diagram of PMF-FFT algorithm

而当多普勒频移落到两个FFT的交点时，由于FFT的引入，造成了较大的增益衰减，即扇贝损失，该衰减在第0点和第1点FFT交点处最为明显[15]，于是在PMF-FFT算法中的部分匹配滤波器输出后加海明窗，海明窗的频谱特性如图5 所示. 在P个匹配滤波器后加海明窗函数，改进的PMF-FFT算法原理如图6 所示.

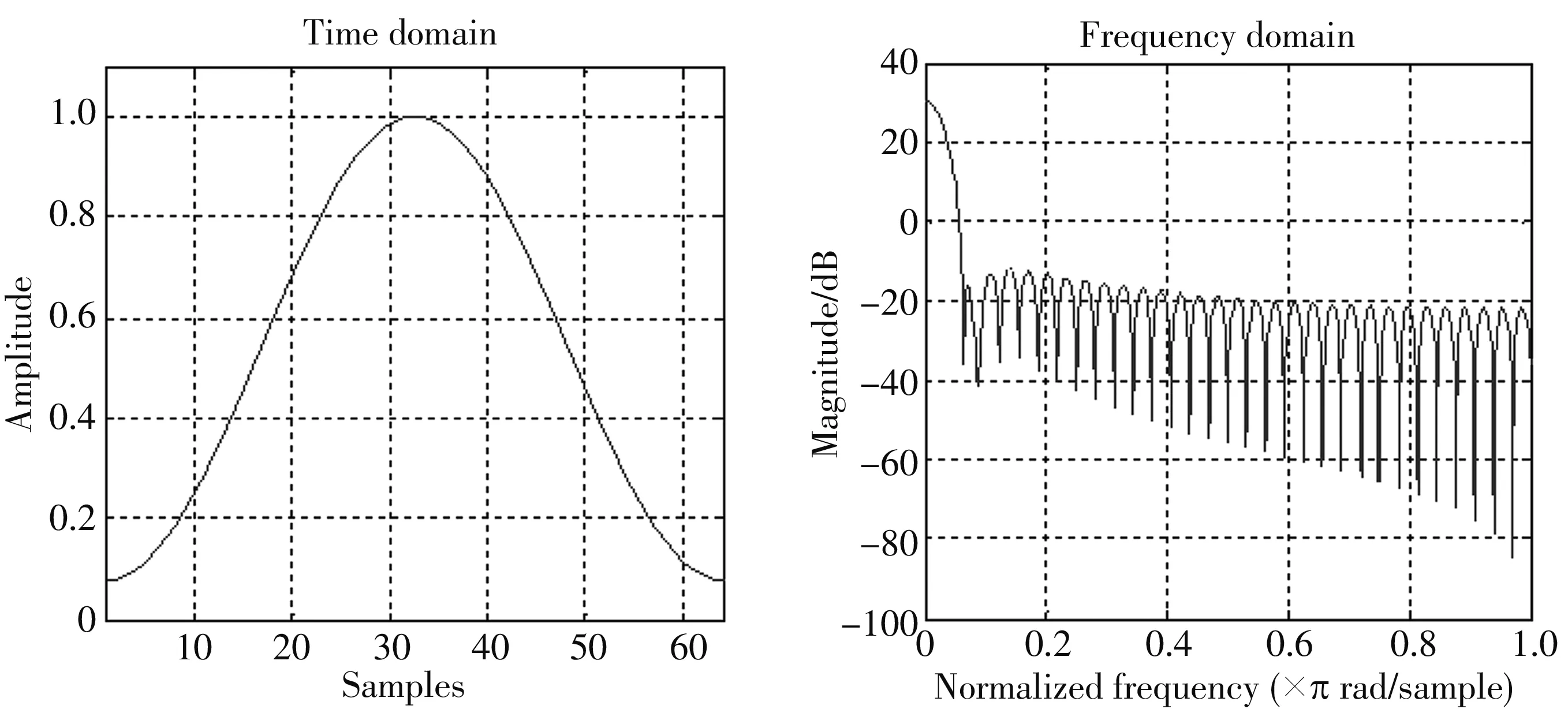
图5 海明窗频率响应

海明窗的数学表达式为

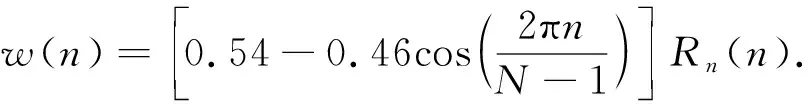
(8)

接收到的信号经过下变频与采样之后的量化输出信号为

r(k)=PN(k)ej(2πfdkTc+φ),

(9)

式中：PN(k)为伪码序列；Tc为码元宽度；fd为信号载波的多普勒频移.

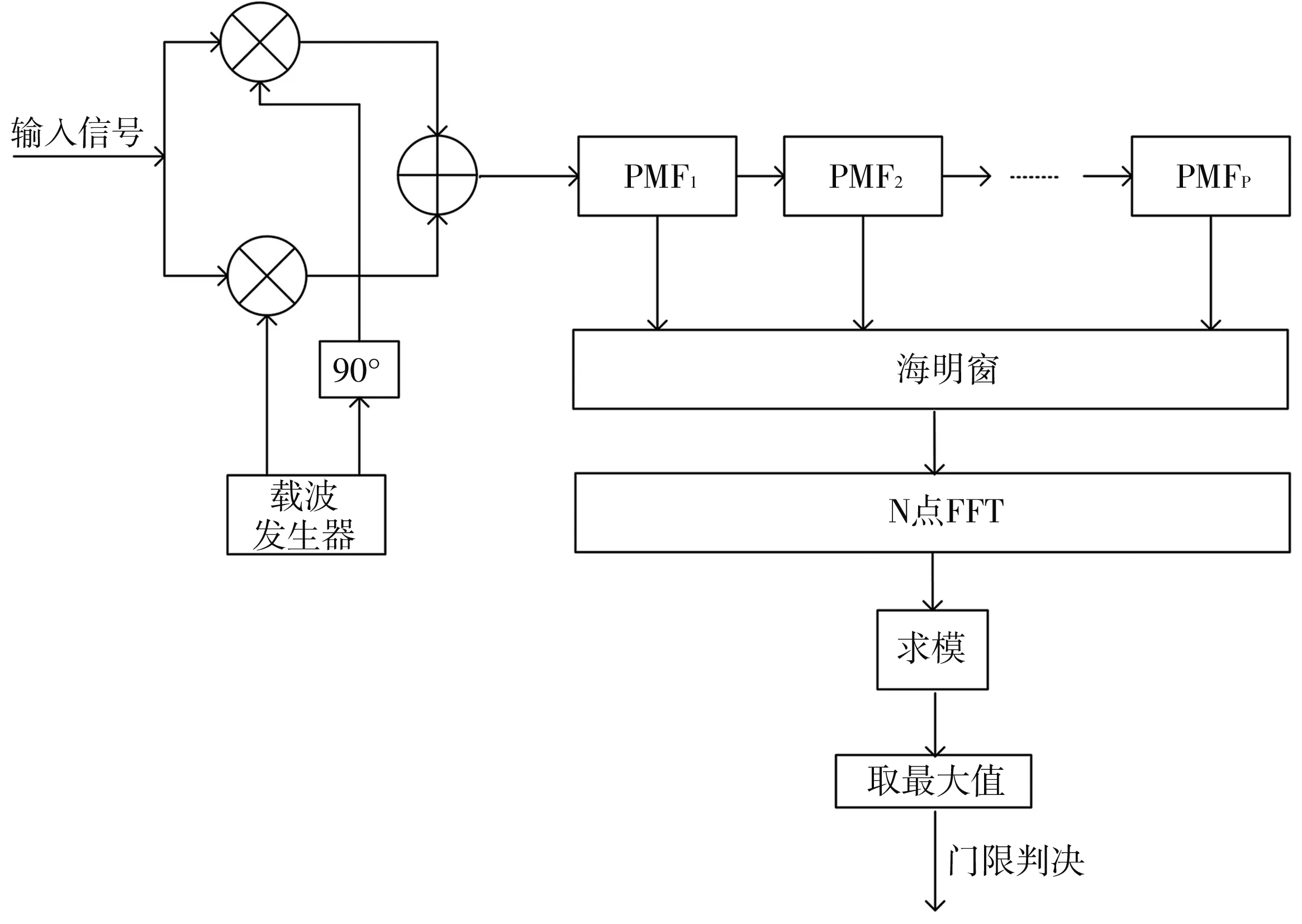
图6 改进的PMF-FFT算法原理图

在本地序列与接收序列同步时有PN(k)PN(K+k)=1，其中K为本地序列与接收序列的偏移量. 信号经过第一个部分匹配滤波器后，输出为

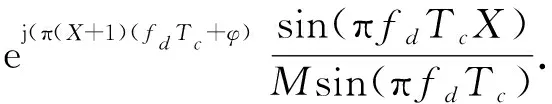
(10)

同理，信号经过第n个部分匹配滤波器，输出为

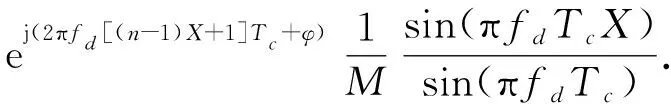
(11)

将这P个部分匹配滤波器的输出进行N点FFT计算得到的归一化增益

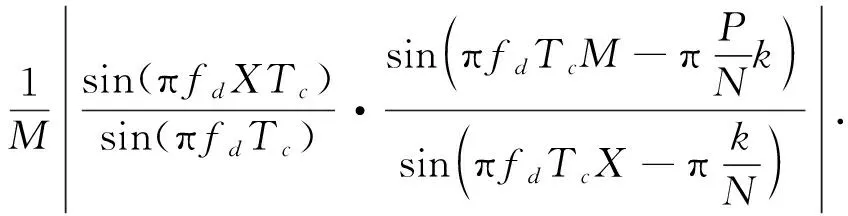
(12)

PMF-FFT的归一化增益如图7 所示.

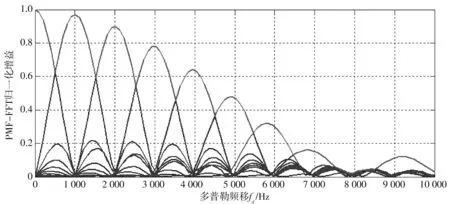
图7 PMF-FFT归一化增益

式(11)可以写为两部分的乘积，即

G(fd,k)=G1(fd)·G2(fd,k),

(13)

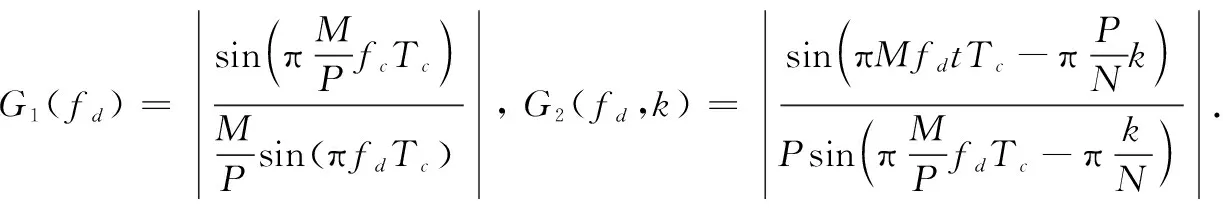
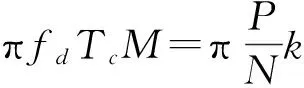
3 实验仿真及结果分析

由于伪噪声码的自相关特性，通过模拟信号发生器的原理，将接收到的信号下变频后与本地产生的伪码进行相关运算，当最大值高于判决门限时，捕获成功. 本地伪码产生原理如图8 所示，码速率为2.046 Mcps，码长为2 046，其由线性序列G1和G2进行模二加运算后产生平衡Gold码，再截短最后一个码片生成.G1序列和G2序列均由11级线性移位寄存器生成，生成多项式分别为

G1(X)=1+X+X7+X8+X9+X10+X11,

(14)

G2(X)=1+X+X2+X3+X4+X5+

X8+X9+X11.

(15)

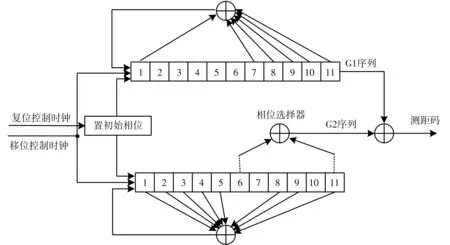
图8 CB1I码发生器示意图Fig.8 Schematic diagram of CB1I code generator

图9 为产生的本地CA码的前500位Gold码.

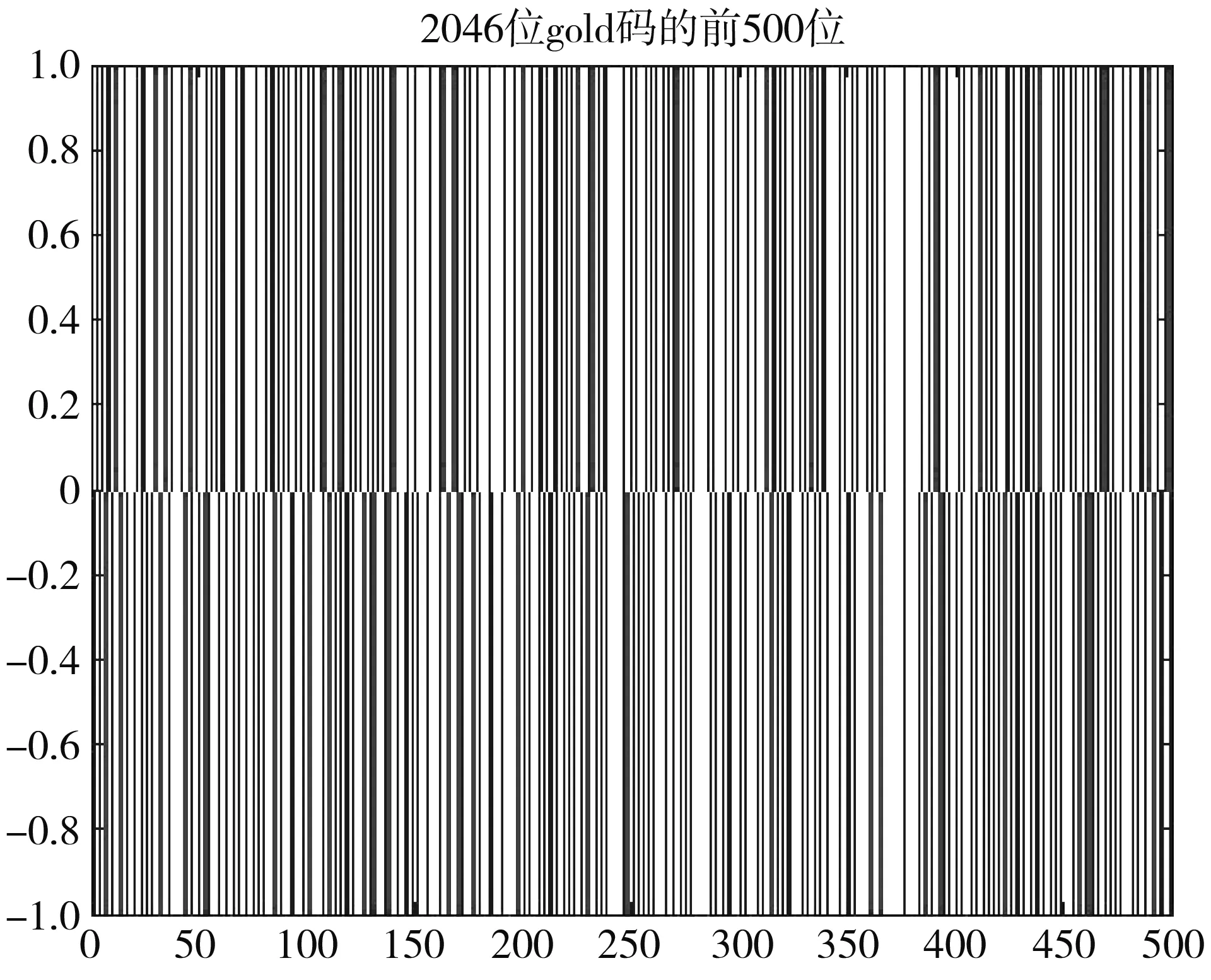
图9 17号卫星的部分伪码Fig.9 Partial pseudo code of satellite 17

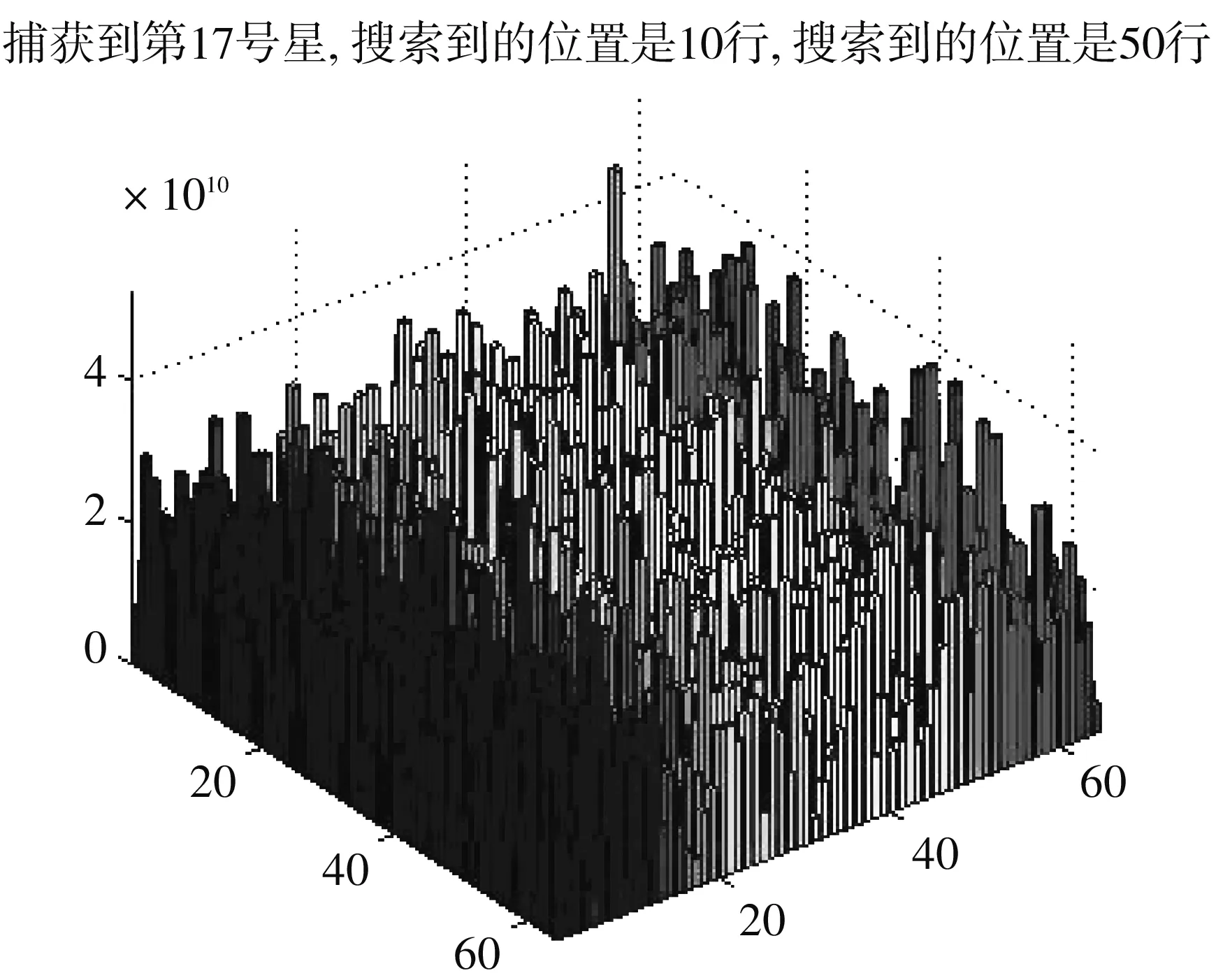
图10 捕获到卫星的位置Fig.10 Satellite’s position captured

利用基于PMF-FFT算法进行加窗函数的改进算法，对17号卫星信号进行捕获，在仿真时，对2 ms数据的末4位补4个1，得到4 096个点，经过变换得到64*64的矩阵，同时，取本地的2周期CA码，将其同样变换为64*64的矩阵形式，然后将这两个矩阵的对应元素相乘，该过程即为数据经过64段长度为64的部分匹配滤波器，将这64个结果的模的和经过海明窗后输入64位FFT，最后将FFT的结果进行IFFT变换，将结果的模与门限值比较，高于门限时捕获成功，捕获结果如图10 所示.

经过仿真，在矩阵的第10行、 50列捕获到了17号卫星，相比于传统并行捕获算法的运算量73 728，加海明窗的改进的PMF-FFT算法同样对2 ms数据信号捕获的运算量为576，运算量远少于传统捕获算法，捕获时间大大减少了. 算法中FFT使得匹配滤波器的幅频响应在频率上延伸，如图11 所示； 使用海明窗对FFT带来的扇贝损失进行弥补，由图12 可看出，在原算法的基础上增加海明窗后，匹配滤波器的增益衰减降低，捕获概率提高.

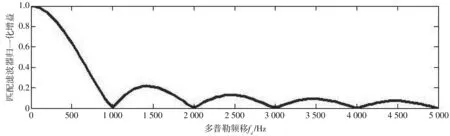
图11 匹配滤波器归一化增益

4 结 论

针对传统的时域串行捕获算法与基于FFT的并行码相位捕获算法存在时间复杂度高而造成捕获较慢的问题，本文采用了改进的PMF-FFT捕获算法. 捕获信号时，取2 ms输入信号，在4 092位数据末位补4个1后转换成64*64的矩阵形式，与做了同样变换的2个周期的本地伪码对应数据相乘实现部分匹配滤波器相关运算，极大地减少了计算量，提高捕获速率； 其次在匹配滤波器输出的数据后加海明窗函数，减小了匹配滤波器由FFT带来的扇贝损失，而加入FFT增加了匹配滤波器的幅度响应的频率范围，综上所述，加海明窗后的PMF-FFT算法可以对卫星实现准确的捕获，捕获速度更快，捕获概率更高.