基于栈式自编码神经网络的脑电信号情绪识别
2021-05-13乔晓艳
刘 鹏,乔晓艳
(山西大学 物理电子工程学院,山西 太原 030006)
0 引 言
情绪无时无刻不在影响着人们的工作生活,如果能使计算机具有识别人类情感的功能,将会在医疗、 教育、 养老、 娱乐、 人机交互等多个领域产生巨大的促进作用. 目前,自动情绪识别的研究,包括离散和连续情感模型的生理和非生理信号情绪识别. 连续维度情感模型较离散情感模型而言,可以更加准确地刻画人的情绪状态,贴合人的真实感受,成为了各国研究人员在情绪识别方面的追求目标. Koelstra等人[1]在DEAP数据集上提取脑电(EEG)信号δ,θ,α,β节律功率谱特征,使用朴素贝叶斯(NB)分类器在效价、 唤醒度上进行分类,正确率最高分别达到57.6%和62.0%; Li等[2]在DEAP数据集上通过小波尺度变换将多导联神经生理信号封装成网格状帧,结合卷积神经网络(CNN)和递归神经网络提取任务相关特征,在效价和唤醒度两个维度上进行情绪识别,算法平均正确率分别为72.1%和74.1%; Liu等[3]在DEAP数据集上提取脑电信号特征,通过组合最大相关性最小冗余和主成分分析融合了高维特征,使用支持向量机(SVM)进行分类,在效价和唤醒度上分类正确率分别为72.4%和76.1%. 阚威等[4]在DEAP数据集上将脑电信号划分为多个时间段后分别提取其特征,采用长短时记忆(LSTM)算法进行维度情感分类,正确率分别为73.9%和73.5%; 晁浩等[5]先在DEAP数据集中提取脑电信号表征的情感初始特征,通过深度信念网络(DBN)将初始特征进行高层抽象表示,再利用受限制玻尔兹曼机实现情感分类,在效价和唤醒度二维情感维度上分别得到78.2%和77.1%的正确率.
目前,在脑电生理信号情绪识别中,基于维度情感模型的连续情绪识别正确率普遍不高,无法满足实际应用需要,而且分类过程中存在情感类别标签划分不统一、 情绪生理特征个体差异较大、 提取的与情绪相关的生理信号特征不充分、 差异也不显著[6]. 因此,本文针对这些问题,在维度情感数据集上,对音乐视频诱发下的情绪脑电信号进行多角度特征提取、 归一化脑电处理以及情感标签分析,在此基础上设计栈式自编码深度学习算法实现情绪的有效分类,获得了较好的识别正确率,为实现生理信号情绪自动分析和识别奠定坚实基础.
1 维度情感模型
1.1 DEAP数据集
DEAP数据库[1]是由Koelstra等研究人员开发的开源数据集,主要用于研究生理信息的情绪识别. 它记录了32名被试观看音乐视频时的脑电数据和外围生理数据,并对音乐视频在维度空间进行情感标注. 每个被试者分别观看40个精心挑选的时长60 s的音乐视频(MV),每个视频有对应的维度情感标签. 同时利用生理测量仪采集记录被试者的生理数据,每次实验还记录了3 s自然状态下的生理数据,以及被试者根据效价、 唤醒度、 控制度、 相似度对每个视频的评分. 此外,对于32名被试者中的22名,记录了观看音乐视频时的面部表情. 实验以512 Hz的采样率记录脑电信号,并经过预处理之后降采样为128 Hz. DEAP数据集中每名被试者的数据内容包含了40个音乐视频诱发下的40通道生理数据和4个维度的情感标签数据,如表1 所示.

表1 DEAP数据集内容
本文选取与情绪最相关的左右大脑半球对称的8个导联脑电数据进行研究,对应的导联分别为fp1,fp2,f3,f4,p3,p4,o1,o2.
1.2 情感模型与标签选取
本文情绪标签生成基于数据集中测试者对MV的情绪评价. 在生成情绪标签之前,涉及到如何对情绪进行划分的问题以及采用何种情感模型的问题. 在DEAP数据集中,被试者对MV的评价是从4个维度来量化情绪的,分别是效价、 唤醒度、 相似度和控制度. 效价和唤醒度是目前大多数研究采用的维度情感模型,效价代表个人的正负性情绪状态,如高兴和不高兴. 唤醒度表示情感的强度,如平静和兴奋. 效价、 唤醒度的情感标签评分范围均为1~9. 神经生理学研究表明效价和唤醒度可以很好地刻画人的不同情绪状态,本文正是基于这两个维度进行情绪识别研究.
在情绪分类问题中,对情感标签的划分是实现情绪分类的前提,由于人不仅有正性与负性情绪,往往还会有介于两者之间的情感状态; 在情绪强烈程度上,除了强弱之外还会出现平静状态,因此情感识别要充分考虑到情绪的不同状态. 只有准确标定情绪状态,在机器分类中才能更准确地识别情绪. 为了探索这种模糊情绪状态对识别结果的影响,本文对效价和唤醒度分别采用不同的情绪标签阈值进行维度情绪状态划分. 第一类情况: 情绪标签分值大于7作为高效价高唤醒度,小于3作为低效价低唤醒度; 第二类情况: 情绪标签分值大于6作为高效价高唤醒度,小于4作为低效价低唤醒度. 通过选取不同标签阈值,分析情绪的模糊程度对识别结果的影响. 以上两种不同阈值情况下,DEAP数据集对应于效价和唤醒度情感标签的样本数量也不同,如表2 所示.

表2 数据集效价和唤醒度样本个数
2 脑电特征提取
脑电信号特征主要由时域特征、 频域特征、 时频特征及非线性特征构成[7]. 由于情绪脑电信号的复杂性以及脑电个体差异性,对于每个被试者记录时长为63 s的脑电信号,对应减去前3 s自然状态的脑电数据,可获得被试者情绪诱发的脑电信号,并可消除个体差异. 然后,提取情绪脑电信号时域、 频域、 非线性特征并进行归一化处理,并进行不同特征组合.
2.1 频域特征提取
已有研究表明,脑电活动的θ(4 Hz~8 Hz),α(8 Hz~13 Hz),β(13 Hz~30 Hz)和γ(30 Hz~45 Hz)节律与人的心理和情绪状态具有密切关系. 因此提取脑电频域特征时,先将信号映射到对应频段上,然后得到各个频段上的特征量. 由于脑电信号是随机信号,本文采用AR模型功率谱估计方法进行频域分析和特征提取. AR模型又称自回归滑动平均模型,估计模型参数需要求解Y-W方程[8]. AR模型的系统函数
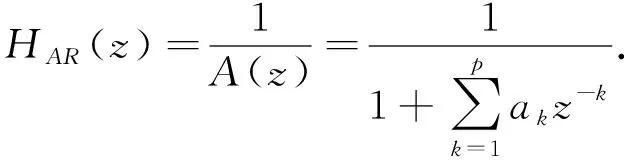
(1)
模型输出功率谱
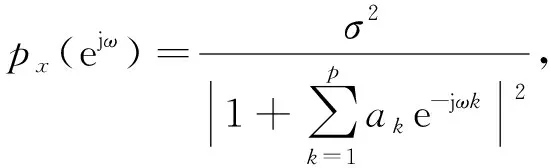
(2)
式中:ak是模型参数,P为阶数,Burg算法可以快速实现模型参数估计.
采用AR模型方法获得EEG信号的功率谱,进而计算脑电各个节律对应的谱能量或功率,作为脑电θ,α,β和γ节律的频域特征.
2.2 时频特征提取
小波包变换是一种分析非平稳过程的有效方法,提供了更为精细的信号分解,它将频带进行多尺度划分,对多分辨率分析没有细分的高频部分以二叉树方式分解成等频带宽的子空间,并根据被分析信号的特征,自适应地选择相应频带,使之与信号频谱相匹配,从而提高时频分辨率[9].
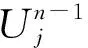
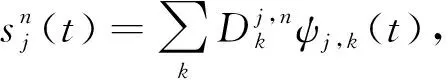
(3)
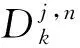
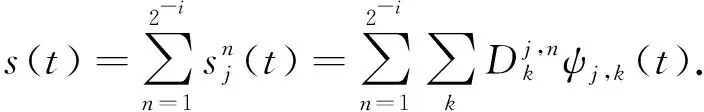
(4)
小波包节点能量可以有效表示信号能量,定义小波包节点能量
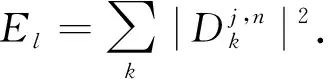
(5)
信号总能量可以表示为不同频带小波包节点能量之和,即
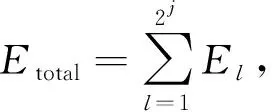
(6)
则小波包能量占比
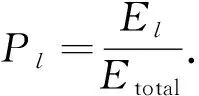
(7)
它反映了脑电各个频带对应的小波包能量分布情况.
本文采用db3小波对EEG信号进行了3层小波包分解,重构后提取了8个节点对应的小波包系数均值、 标准差及小波包节点能量占比等时频特征. 图1 所示为小波包重构后各节点的EEG信号波形.
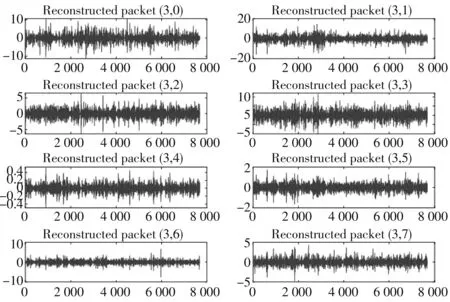
图1 小波包重构后各节点的EEG波形Fig.1 EEG waveform of each node after waveletpacket reconstruction
2.3 非线性特征
样本熵反映了时间序列的复杂度,能够衡量时间序列中产生新模式概率的大小,样本熵值越大,产生新模式的概率越大,序列越复杂. 不同情绪状态下,对应大脑皮层被激活的程度不同,脑电活动的复杂性也不同. 因此,样本熵特征可以反映情绪脑电的变化. 样本熵
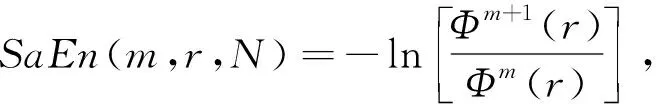
(8)
式中:N为时间序列的长度;r为选定的相似容限值;m为模式维数.Φm+1(r)迭代计算步骤如下[10]:
1) 对一个长度为N的时间序列[x(1),x(2),…,x(N)],按顺序重构m维相空间得到Y(i)=[x(i),x(i+1),…,x(i+m-1)]和Y(j)=[x(j),x(j+1),…,x(j+m-1)],其中i,j=1,2,N-m+1;
2) 定义Y(i)与Y(j)之间的距离d[Y(i),Y(j)]为两者对应元素中差值最大的一个,即
d[Y(i),Y(j)]=

(9)
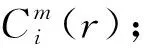
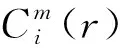
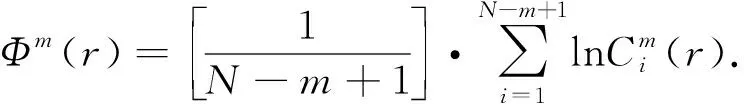
(10)
5) 设定嵌入维数m+1,重复步骤1)~4),得到Φm+1(r);
本文选取嵌入维数m为2,阈值距离为0.2倍的信号标准差.
小波包熵反映了随机序列的不确定性,小波包熵值越大表明序列无序性越强[9]. 脑电信号的小波包熵与情绪状态密切相关,在不同情绪诱发下,大脑神经元抑制/兴奋状态发生变化,导致脑电序列的无序性随之发生变化,故可提取脑电的小波包熵进行情绪识别,小波包熵
WEP=-∑Plln[Pl],
(11)
式中:Pl为式(7)所提取的小波包能量占比.
综上所述,本文提取情绪脑电信号频域、 时频域和非线性共30个特征,如表3 所示. 对这些特征进行不同组合,构成对应特征向量,可以研究多特征融合对脑电情绪识别的影响.

表3 提取的情绪脑电特征
3 栈式自编码的维度情绪识别
栈式自编码神经网络算法是一种半监督的深度学习算法. 它借鉴大脑神经元兴奋性机制,利用稀疏自编码器对数据逐层预训练,获得网络初始权值和阈值,然后通过多层神经网络反向传播调节优化整个网络权值. 稀疏性减少了实际计算量,自编码优化了初始权值,因此算法具有收敛速度快、 不易陷入局部极小的优点. 此外,深层的栈式自编码算法还具有自动训练优化特征的优点. 栈式自编码神经网络由稀疏自编码器和softmax分类器构成,结构如图2 所示.
稀疏自编码器由输入层、 隐层、 输出层组成多层深度神经网络,采用逐层贪婪训练方法使自编码器的输出值无限趋近于输入值[11]. 训练稀疏自编码器的代价函数为
Jsparse(W,b)=‖hw(X)-X‖2+β∑|hj|,
(12)
式中:β控制稀疏性惩罚因子的权重; 第一项为输出值与输入值的二范数,使输出结果与输入逼近; 第二项为隐藏层神经元激活输出的一范数,作为稀疏自编码器的稀疏性限制. 将训练好的稀疏自编码器连接softmax回归模型,通过反向传播算法从Softmax输出层到隐层逐层对代价函数求偏导,微调各层权值向量,对整个网络进行迭代优化,分类器计算对应标签的概率P(j|H(2))并输出分类结果.

图2 栈式自编码算法结构图Fig.2 Structure diagram of stack auto-encoder algorithm
本文栈式自编码神经网络的输入层节点为脑电特征向量,输出层节点数为2,即维度情绪状态. 通过仿真试验,选择了两个隐含层,第一隐层节点数为15,第二隐层节点数为7. 网络训练样本和测试样本按照4∶1分成训练集和测试集. 图3 为网络训练的单次学习曲线(锯齿状)和平均学习曲线(线状). 从中可以看出,网络训练在开始迭代时震荡较大,当迭代达到600次时误差目标函数下降到0.001,网络参数训练达到最佳. 将训练好的栈式自编码网络利用测试集样本进行分类测试,可获得情绪识别正确率
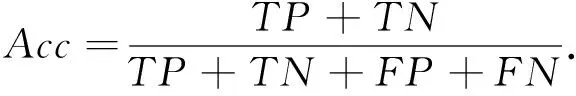
(13)
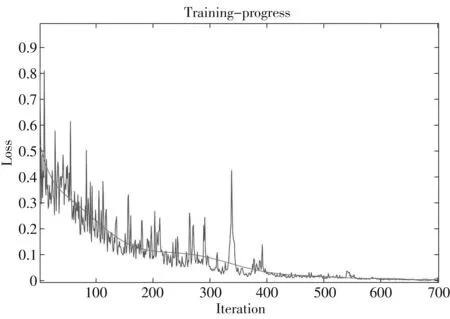
图3 栈式自编码算法学习曲线Fig.3 Learning curve of stack auto-encoder algorithm
此外,引入正类、 负类样本的召回率RT,RN作为评价指标,计算公式为
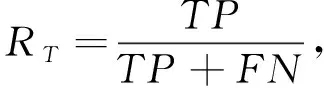
(14)
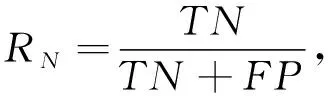
(15)
式中:TP,TN分别表示被正确分为正类或负类的样本个数;FP,FN表示被错误分为正类或负类的样本个数. 本文计算识别正确率时,将网络输出高效价、 高唤醒度的样本记为正类样本,输出低效价、 低唤醒度的样本记为负类样本.
将本文提取的情绪脑电特征,应用栈式自编码算法进行维度情绪识别,并与使用DEAP数据集的其它方法进行对比,如表4 所示. 从表4 中可以看出,无论是效价情绪维度还是唤醒度情绪维度,本文采用的栈式自编码算法对维度情绪识别的正确率均高于其他3种方法,表明了该算法应用于脑电情绪识别的有效性.

表4 不同分类方法结果对比
4 结果与分析
本文主要从3个方面进行仿真分析: ① 样本数据均衡对情绪识别结果的影响; ② 脑电特征对情绪分类的影响; ③ 情感标签划分对识别结果的影响.
4.1 样本数据均衡对情绪识别的影响
由表2 中可以看出,无论是在效价还是唤醒度维度上,用于分类识别的数据样本量相差较大. 为了探究这种数据不均衡对算法分类结果的影响,本文设计了两种方式下的情绪分类,第一种方式是不对样本数量进行处理,将所有样本数据按照4∶1 划分为训练集和测试集进行训练和测试; 第二种方式是对数据进行均衡处理,即在每个情感维度上(效价、 唤醒度)选取的样本数据基本平衡,即维度情绪标签数量相等. 具体做法是: 按照样本数量少的那个,选取对应维度的样本数量,之后再按照 4∶1 划分为训练集和测试集. 按照式(13)~式(15)计算正确率及两类样本召回率,仿真结果如表5 所示.
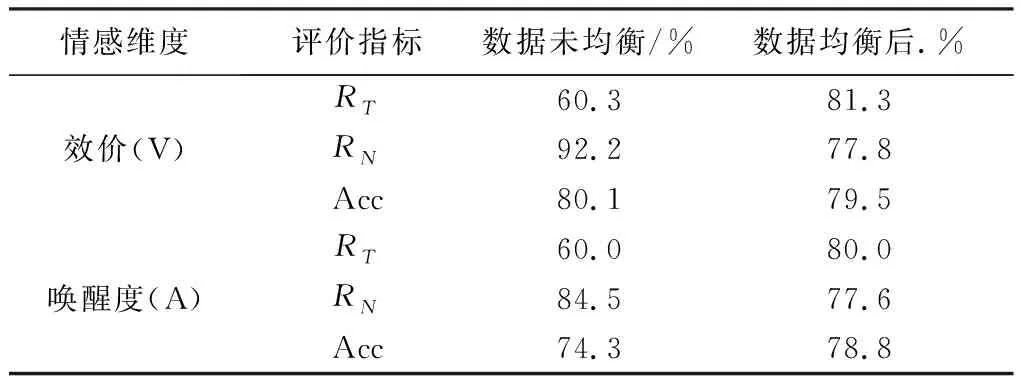
表5 数据均衡与数据未均衡识别结果对比
表5 结果显示,数据样本均衡或者不均衡,效价维度情绪的识别正确率相差不大,均在80%左右,唤醒度维度情绪识别正确率相差4.5%. 但是考察两类样本召回率时,可以发现数据不均衡时,低效价情绪召回率为92.2%,高效价召回率为60.3%,其结果相差很大,同样,低唤醒度情绪召回率为84.5%,高唤醒度召回率为60.0%,这是由于数据样本不平衡导致的. 数据均衡后,不同维度情绪状态的识别正确率大体相同. 综上可知,在脑电情绪识别中,有必要对样本数量进行均衡化处理,可以提高算法的稳健性.
4.2 不同特征组合对分类结果的影响
本文从频域、 时频域和非线性多个维度提取了情绪脑电特征,为了验证特征的有效性并获得最佳化的特征,选用不同脑电特征组合,经过数据均衡化处理后,研究对分类正确率的影响,如表6 所示.
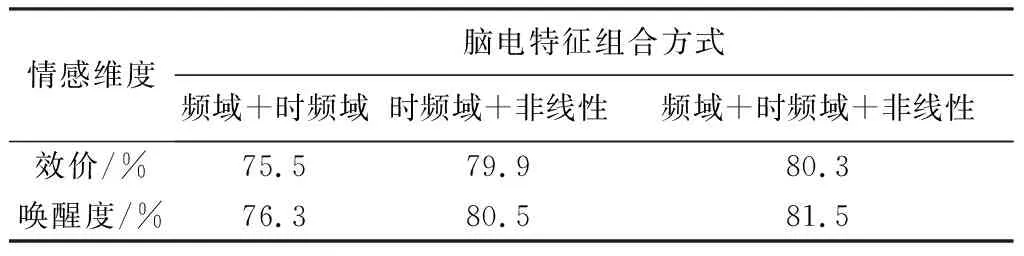
表6 不同特征组合结果对比
表6 结果显示,在唤醒度及效价维度上,3种特征组合用来分类情绪的正确率相比频域和时频域特征组合平均高出6%左右,比时频域和非线性特征组合平均高出3%左右. 由此可以得出结论: 选用频域、 时频域、 非线性3种特征组合可以更好地表征不同情感状态,情绪识别正确率更高,因此尽可能提取情绪脑电多种特征,可以更充分挖掘脑电信号中蕴含的情绪信息.
4.3 情感标签阈值对分类结果的影响
将效价和唤醒度两个情绪维度上的数值按照不同阈值设定,划分为两大类. 第一类阈值设定效价值小于3为低效价,大于7为高效价; 第二类阈值设定效价值小于4为低效价,大于6为高效价. 唤醒度也采取同样方法设定情感标签阈值. 经过数据均衡化处理,选用3种组合特征进行情绪分类,分类正确率结果如表7 所示.

表7 不同情感标签阈值分类正确率对比
表7 结果显示,无论是效价还是唤醒度,第一类阈值设定的情绪识别正确率均大于第二类阈值设定. 原因在于第一类阈值的情绪状态,无论是唤醒度还是效价,情绪表现更加强烈和明确,因而更有利于机器识别; 第二类阈值的情绪状态更加模糊化,因而较难以识别. 由此表明,在对情绪进行维度标签时,阈值设定合适有助于提高情绪识别正确率.
5 结束语
本文基于DEAP数据集对EEG信号进行了频域、 时频域和非线性特征提取,并利用栈式自编码算法在效价及唤醒度两个维度对情绪进行分类识别. 与其他方法相比,取得了更高的识别正确率,表明栈式自编码深度学习算法对EEG情绪识别的有效性. 仿真结果表明: 对数据进行均衡化处理,算法更加稳健; 多维特征进行融合,情绪识别正确率更高; 情感标签的阈值设定对情绪识别结果会产生影响. 该研究可以应用于医疗、 教育、 人机交互等领域的脑电情绪识别.
