放入式电子测压器应用环境下动态校准数据拟合方法研究

赵彦凯，裴东兴，石垒，张瑜

(1.中北大学 电子测试技术国家重点实验室，山西 太原 030051；2.北京航天控制仪器研究所，北京 100039)

膛压作为各类兵器研制和验收的一项重要性能参数，对其进行精确测量一直是改进高膛压火炮发射技术[1]不可或缺的步骤。放入式电子测压器作为一种新型的膛压测试仪器[2]，它有着铜柱测压器[3]可重复使用、避免在武器身管打孔的特点；又有导线电测仪器精度高和能记录p-t曲线的特点,是火炮膛压测试非常理想的测试仪器。在膛压测试的过程中，需要将放入式电子测压器与发射药一起放置到炮弹的药筒内，在发射药燃烧的高温、高压、高冲击环境中直接测量膛压信号。考虑到火炮膛内较为恶劣的工作环境，实验室条件下的静态标定设备无法满足仪器的校准需求，所以设计了一种在应用环境下的动态校准系统，该系统可以模拟膛内恶劣的工作环境，是现阶段最理想的校准方法。

在校准中，需要求取放入式电子测压器的灵敏度函数，即对校准数据进行线性拟合。这里分别采用普通最小二乘法(LS)和整体最小二乘法(TLS)进行线性拟合。最小二乘法经历了长时间的发展和应用，已经被广泛应用于诸多工程与试验中，该拟合方法能够使观测值与拟合直线的y值之差的平方和最小，是一种非常实用的线性拟合方法。而整体最小二乘法作为一种新的拟合方法可以同时考虑到自变量与因变量的误差[4]，不会因变量选取不同而产生不同的拟合结果，所以在满足一定的使用条件[5]下可以获得更佳的拟合效果。笔者将结合放入式电子测压器在应用环境下动态校准实验，对两种线性拟合方法进行比较，并通过实验与拟合结果来阐述二者的差异。

1 模拟膛压校准系统

1.1 校准系统的组成及工作原理

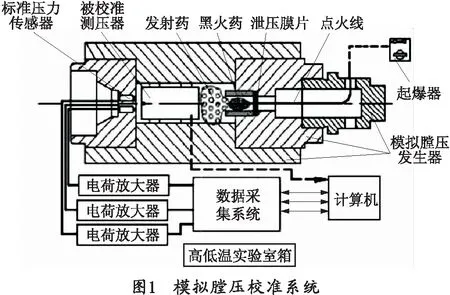
模拟膛压校准系统的设计目的是为了模拟出与火炮身管内尽可能相似的工作环境，用该系统检测放入式电子测压器的动态特性与综合性能指标，整个校准系统的组成结构如图1所示。其中，3支已被校准的标准压力传感器安装在整个装置的底端[6]，与被校测压器相对放置。在校准时，根据不同的需求，往发生器中加入特定量的火药，并使用点火装置点燃发生器中的火药，在这个类似火炮发射的过程中，身管内产生的高压通过传压孔同时施加在3支标准压力传感器和被校测压器上，再由特定的计算机读出存储在数据采集系统中的压力信号。最后将计算机中的3组标准测压器数据与被校测压器数据分别进行数据处理。

1.2 校准试验的数据处理

校准过程采用膛压曲线上升沿的校准方法。选取测压器满量程的95%～100%的压力值作为校准压力峰值，分别在高温(55℃)、常温(25℃)、低温(-40℃)的环境下反复进行多次校准实验，获取3种不同温度环境下的有效校准数据。以3支标准压力传感器的融合压力曲线[7]为基准，将标准测压系统的融合压力曲线与被校测压器压力曲线画在同一个直角坐标系下，逐点平移被校测压器曲线，当二者相关性系数满足要求后停止平移；并选取压力曲线上升沿部分的30%～80%，在这特定的范围内抽取n组数据对作为拟合样本，用整体最小二乘法对n组数据进行线性拟合，拟合结果为测压器在该温度条件下的工作特性方程:

y=kx+b,

(1)

式中:y为压力值，MPa；k是测压器灵敏度系数，MPa/bit；x为某点的bit值；b为截距，MPa.

2 两种线性拟合方法的对比

2.1 普通最小二乘法线性拟合

直线方程可表示为

yi=kxi+b,i=1,2,…,n,

(2)

式中：(xi，yi)为观测点坐标；k、b为待估计参数。

误差方程矩阵表达式为

BδX=l+V,

(3)

式中：δX为待估参数矩阵；B为δX系数矩阵；l为观测向量；V为误差向量。按照最小二乘法的准则

其最小二乘解为

(4)

因变量残差为

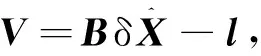
(5)

单位权中误差为

(6)

2.2 整体最小二乘法线性拟合

2.2.1 整体最小二乘法解算方法

整体最小二乘拟合法能同时考虑到两种变量的误差,直线条件方程可描述为

(7)

由EIV模型，误差方程可表示为

(B+EB)δX=l+El,

(8)

式中：δX为待估参数矩阵；EB和El分别表示新构造的系数矩阵B和观测向量l的误差。令

B=[B1B2]，

(9)

式中：B1=[1,1,…,1]T;B2=[x1,x2,…,xn]T.

构造增广矩阵：

A=[Bl]，

(10)

并对增广矩阵A进行QR分解，其中

(11)

可将方程分为两部分：

(12)

(13)

式中,R11，R12，R1l均为标量。

AR=[R22R2l].

(14)

对AR矩阵进行奇异值分解：

AR=UΣNT，

(15)

式中：U=[U1U2…Un-1]，其中U1,U2,…,Un-1均为(n-1)×1矩阵；N=[N1N2]，N1、N2均为2×1矩阵;Σ=diag(σ1,σ2),σ1>σ2.

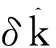
(16)

(17)

2.2.2 整体最小二乘法拟合精度评定

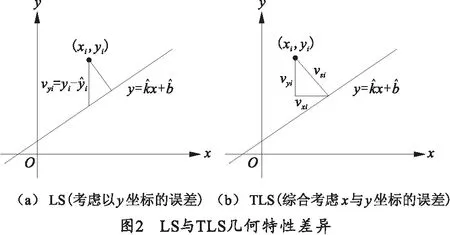
最小二乘法与整体最小二乘法数据拟合的几何特性差异如图2所示，在误差方程(B+EB)δX=l+El中，EB是数字量的改正数，El是压力值的改正数。整体最小二乘法在坐标系x和y方向上的改正数为vxi、vyi，正交方向上的改正数为vsi[8].这里用正交方向的改正量来计算拟合结果的单位权中误差。

增广矩阵AR的改正量为

(18)

R的改正量为

(19)

由此可计算系数矩阵B和观测向量l的改正数，

[EBEl]=[EB1EB2El]=QTER.

(20)

则x方向，y方向的残差为

(21)

正交距离残差为

(22)

单位权中误差为

(23)

在自变量与因变量的误差影响都无法忽略时，整体最小二乘拟合法的数学模型可以同时顾及坐标系中x方向和y方向上的误差，而且从x方向或y方向的改正量和正交距离残差的改正数来看，都要比最小二乘法的残差改正数小，所以单位权中误差的计算值要优于最小二乘法的计算值[9]。

3 校准实验分析与拟合结果对比

选取常温下1#被校电子测压器环境适应性校准实验数据，分别采用最小二乘法、整体最小二乘法进行线性拟合，主要从误差模型、单位权中误差等几个方面对各自的拟合结果进行对比[10]，拟合结果为1#被校测压器在常温状态下的灵敏度函数(工作特性方程[11])。校准实验具体测量数据如表1所示，Matlab计算结果如表2所示。

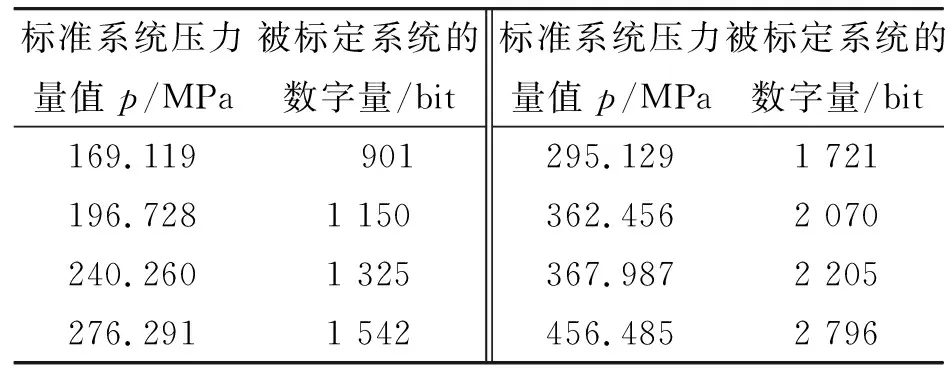
表1 1#电子测压器系统校准数据

表2 1#电子测压器拟合结果对比

由表2中单位权中误差的计算结果可知，整体最小二乘法比普通最小二乘法有着更佳的拟合效果，这是因为拟合时同时考虑了自变量与因变量的误差。但是在传感器的校准实验中，校准是将标准系统所复现的压力标准量值赋予被校准的电子测压器相应的示值，其中示值是自变量(x轴)，压力标准量值是因变量(y轴)，并且自变量与因变量有着固定的对应关系。在该情况下，因变量的误差是可以忽略的，也就是说拟合的真值为校准数据点的因变量(压力标准量值)。所以在拟合直线时应确保真值与拟合直线的y值之差的平方和最小。而拟合直线上的y值与真值之间差值的平方和，才应该用作计算整体最小二乘法的单位权中误差。

表2中整体最小二乘法的单位权中误差为8.140 54，是将压力标准值作为参考值的计算结果。当把压力标准值作为真值时，其单位权中误差为8.237 10.以此类推，对多组放入式电子测压器校准数据用普通最小二乘法和整体最小二乘法进行线性拟合，并同时计算出标准值为真值时TLS的单位权中误差，进行综合比较，汇总结果如表3所示。

表3 普通最小二乘法(LS)与整体最小二乘法(TLS)拟合对比汇总表

由表3的汇总结果可知，在传感器的校准工作中，当测量标准能够给出所校物理参量的真值时，普通最小二乘法单位权中误差的计算值要小于整体最小二乘法单位权中误差的计算值。这是因为从算法上来看，普通最小二乘法的真值在因变量上，而整体最小二乘法的真值在其拟合直线上。由于普通最小二乘法可以实现在一个方向的拟合效果最佳，所以对于放入式电子测压器的校准工作还是最为适用的。

4 结束语

笔者结合放入式电子测压器在应用环境下的校准工作分别对普通最小二乘法(LS)和整体最小二乘法(TLS)的线性拟合效果进行了对比，并同时对传感器校准工作的特殊性进行了分析。需要注意的是，由于放入式电子测压器校准实验本身的特殊性，在该过程中使用普通最小二乘法(LS)进行数据拟合更加合理。只有在无法忽略自变量和因变量误差的前提下，采用整体最小二乘法(TLS)进行直线拟合有望获得更好的拟合效果。