穿甲弹垂直侵彻陶瓷复合靶弹道极限速度的研究

2021-05-13张志倩赵太勇于寅业陈智刚马玥

火炮发射与控制学报 2021年1期

张志倩，赵太勇，于寅业，陈智刚，马玥

(1.中北大学机电工程学院，山西太原 030051；2.中北大学地下目标毁伤技术国防重点学科实验室，山西太原 030051；3.晋西工业集团有限责任公司，山西太原 030051；4. 陆军步兵学院石家庄校区军政训练系装甲车辆工程教研室，河北石家庄 050200)

陶瓷/金属复合装甲在现役武器中得到广泛应用，近年来，国内外学者对弹丸侵彻陶瓷/金属复合靶板的弹道极限速度进行了大量理论研究和试验。1967年Wilkins等在对轻质装甲抗弹性能项目的研究中，用7.62 mm模拟弹作为7.62 mm穿甲弹的替代弹进行了一系列侵彻碳化硼陶瓷复合靶板的试验[1-3]，自此之后，陶瓷/金属复合靶板抗弹性能的研究逐渐成为了装甲防护领域中的热点。2004年杜忠华等[4-6]利用能量守恒建立了杆式弹垂直侵彻陶瓷/Kevlar复合材料靶板抗弹性能的理论分析模型，得出了弹道极限速度的预测公式。2006年申志强[7]在试验和数值模拟研究的基础上，在未考虑陶瓷锥角的情况下，建立了穿甲子弹侵彻陶瓷/金属复合靶板的分析模型。2008年侯二永[8]以弹道试验为基础，结合数值模拟方法，研究了12.7 mm穿甲燃烧弹侵彻陶瓷间隙靶的过程和机理，着重分析了陶瓷间隙靶的间隙效应、厚度匹配和弹着点的影响。2010年卢君等[9]分别对侵彻过程、破坏现象、靶板耗能和极限速度4个方面进行数值模拟研究，并将其结果与试验结果进行了对比分析，得出了碳化硼复合靶板抗弹机理、耗能机制等相关结论。2013年李言语[10]运用ANSYS/LS-DYNA软件对陶瓷/金属复合靶板抗侵彻过程、机理及影响因素进行了分析。2014年Signetti等[11]研究了界面强度和摩擦等关键参数对弹道极限的影响。2017年Ahmad Serjouei等[12]就提高陶瓷弹道性能的试验和数值模拟，对陶瓷/金属双层装甲施加预应力，研究预应力对陶瓷装甲弹道极限的影响。2018年 L.M.Bresciani等[13]基于伯努力方程，改进分析模型并与弹道测试的试验数据进行了对比，该模型可预测弹芯的剩余速度和剩余质量。在前人大量研究的基础上，笔者基于能量守恒，综合考虑陶瓷半锥角和弹芯质量损失耗能，提出弹道极限速度理论分析模型，结论与试验和数值模拟结果比较具有较好的一致性。

1 分析方法

1.1 理论分析

对于穿甲弹垂直侵彻陶瓷/金属靶板，假设穿甲弹以初始速度v0冲击复合靶板，能量损耗转换为陶瓷面板耗能、粘结层耗能、金属背板耗能和弹芯质量损失耗能四部分，如图1所示。在侵彻复合靶板剩余速度为vs=0，则初始速度v0为弹道极限速度v50，即v50=v0，根据能量守恒原理，对陶瓷复合靶板的抗弹性能进行分析。

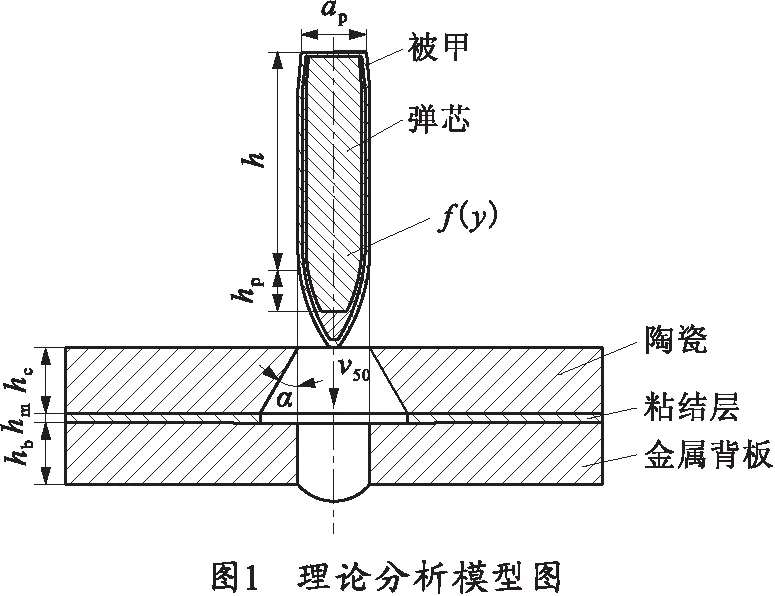
陶瓷材料的抗压极限应力作用的体积为子弹侵彻陶瓷面板消耗的能量Ec，则有[4]：

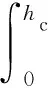
(1)

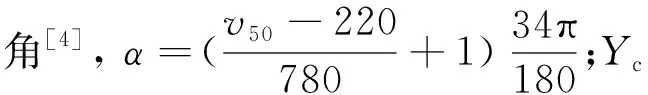
粘结层为纤维材料，冲击压缩撕裂失效的吸收能量为剪切应力作用的体积，以冲击压缩撕裂失效的吸收能量为[4]

π(ap+hctanα)2hmσYS，

(2)

式中：σYS为粘结层的剪切应力；hm为粘结层的厚度。

金属背板为塑性变形耗能，其表达式为[14]

(3)

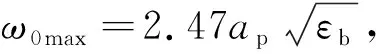
弹芯质量损失的耗能计算，由Tate模型，弹头进入接触面部分在高压下被磨蚀，弹体靠近接触面部分达到其动抗压极限强度，而其余部分近似为刚体，且在阻力YpA(t)的作用下运动速度不断减小，其运动方程为[16]

(4)

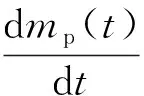
(5)

式中：Ap(t)为t时刻弹芯的横截面积；ρp为弹芯密度；mp(t)为t时刻弹芯的质量；vp(t)为t时刻子弹的速度。

联立式(4)和(5),经化解后积分可得出关于为弹芯质量损失Δmp的表达式，再按泰勒展开式保留首项为

(6)

式中：v50为弹道极限速度；mp0弹体初始质量;Yp弹体的抗压极限应力。

弹体的抗压极限应力Yp作用的体积为质量损失耗能Ep：

(7)

利用能量守恒关系则有：

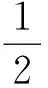
(8)

可以得到弹丸的弹道极限速度表达式为

(9)

1.2 试验研究

试验在地下目标毁伤技术国防重点学科试验室进行，采用线膛弹道枪发射7.62 mm制式弹，通过调节火药装填量调节发射速度，测速设备采用测速仪，试验场地布置如图2所示，制式弹与陶瓷/装甲钢复合靶分别如图3、4所示。

1.3 数值模拟

应用数值仿真的方法进一步预测子弹剩余高度，采用LS-DYNA动力学软件进行数值模拟。在垂直侵彻环境，建立1/4轴对称3D侵彻模型。计算网格均采用Solid 164八节点六面体单元，模型图如图5所示，在进行网格划分时，子弹与复合靶直接接触区及附近划分较密的网格，而远离弹道的区域尺寸逐渐增大，有效提高了计算速度。陶瓷面板材料采用JH-II模型，材料参数见文献[17]，装甲钢靶均采用ELASTIC_PLASTIC_HYDRO塑性本构模型和GRUNEISEN状态方程，具体参数如表1所示。

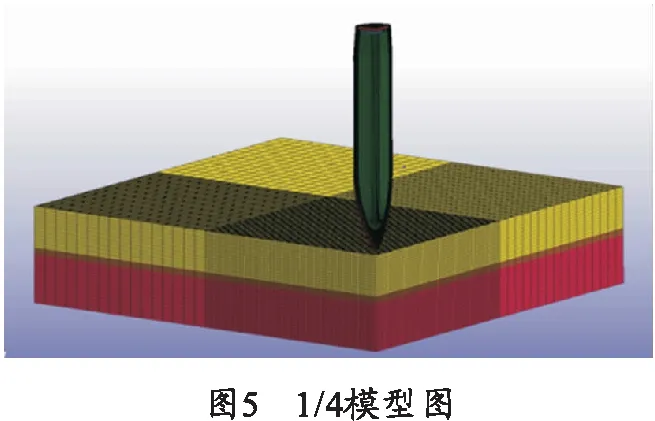
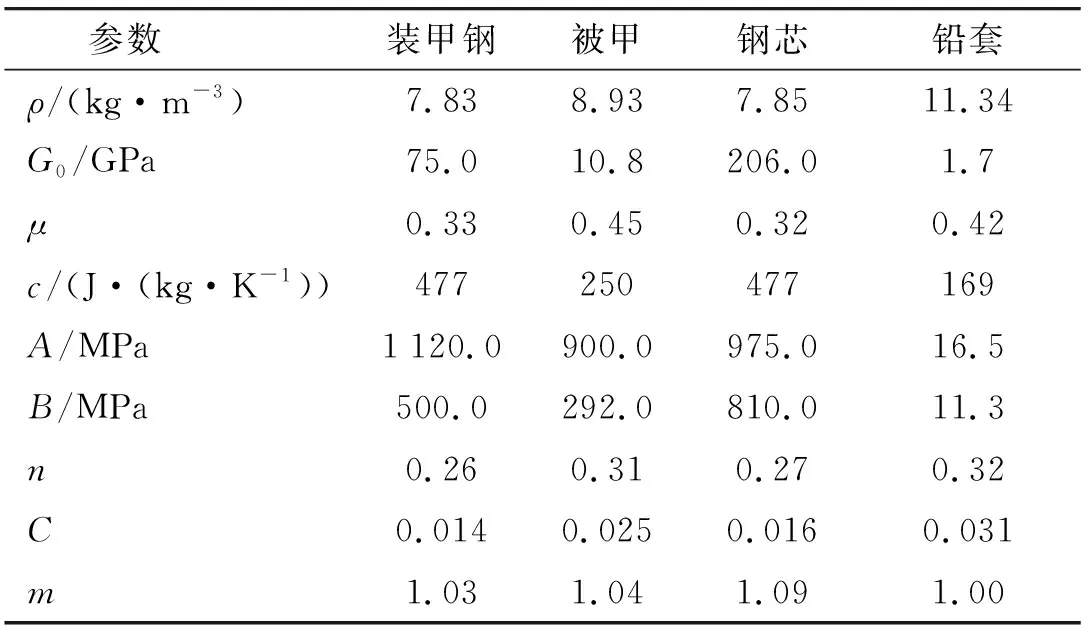
表1 材料性能具体参数

2 结果与分析

2.1 弹道极限速度分析

进行7.62 mm穿甲子弹穿靶试验的子弹速度为608～857 m/s，将试验回收的子弹弹芯和弹头与速度为v50时数值模拟的剩余子弹钢芯及弹头壳式样进行对比，如图6所示，回收钢芯式样具体参数如表2所示。发现回收的弹芯和壳体发生不同程度的断裂，随着冲击速度的增大，质量侵蚀范围增大，同时弹尾部剩余高度逐渐减小，试验均没有回收到弹丸圆弧头部，可见在陶瓷/金属靶的抗冲击作用下，弹丸头部质量均侵蚀断裂。

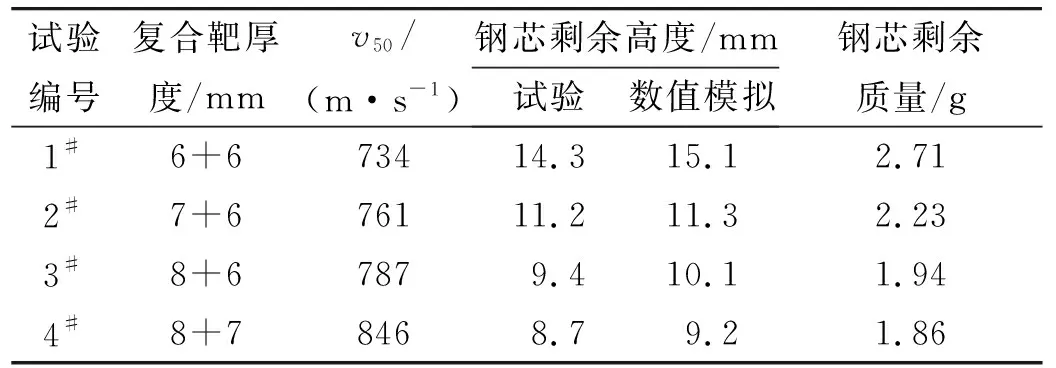
表2 回收钢芯式样参数

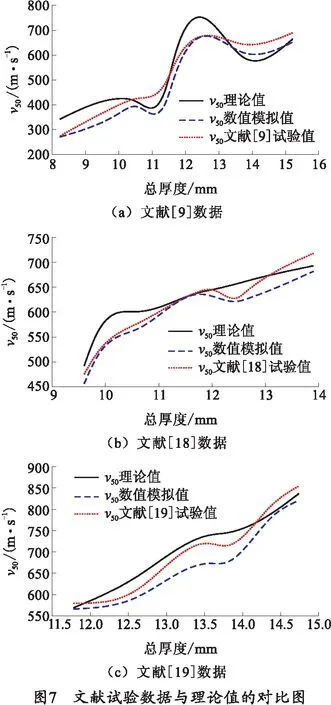
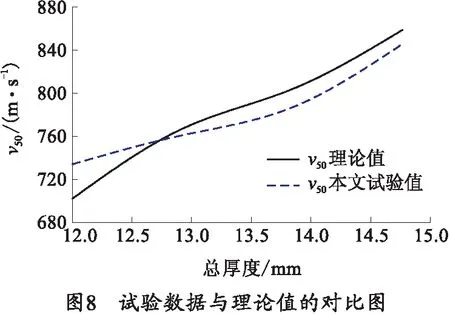
对文献[9]、[18]、[19]中的试验数据进行验证计算，将理论计算值、试验数据值和数值模拟值三者结果对比，如图7所示。图7(a)、(b)、(c)中金属背板分别为铝、钢、铝，考虑弹芯质量损失的理论计算模型、文献试验数据和数值模拟值吻合较好，结果表明运用该模型计算出的理论值与试验值误差范围在10%以内。结合理论分析模型算出的v50和本文中的试验值的v50进行对比，发现两者吻合较好，如图8所示。因此，笔者提出的理论分析模型和数值模拟结果具有参考价值。

基于提出的理论模型的可靠性，进一步研究复合靶各个部分耗能占比。由文献[9]、[18]、[19]中不同厚度的复合靶板数据，利用式(1)、(2)、(7)计算出不同金属钢背板厚度下击碎陶瓷耗能、粘结层耗能和弹芯质量损失耗能的比例，如图9所示。

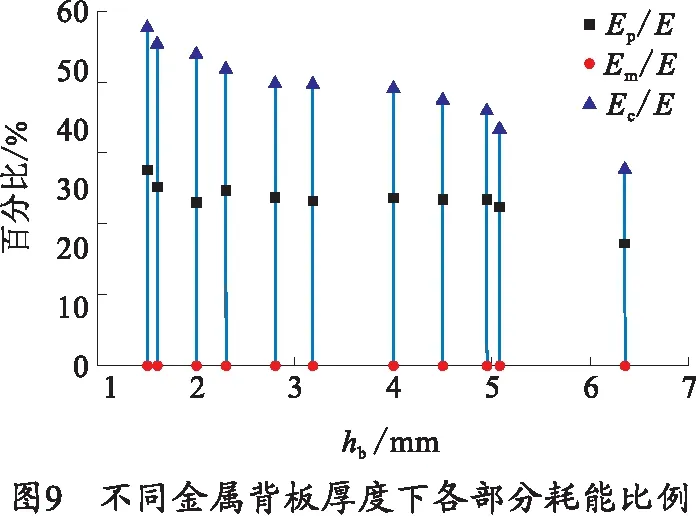
研究发现：粘结层的耗能比例(圆点)小于5%，击碎陶瓷耗能(三角形点)比弹芯质量损失耗能(方点)多，且在相同金属背板厚度，陶瓷越厚，击碎陶瓷耗能比例越高；随着金属背板厚度的增加，陶瓷耗能的比例逐渐减小；弹丸质量损失耗能在20%～40%，因此弹丸质量损失的能量是不可忽略。

基于理论模型和数值模拟的可靠性，进一步研究陶瓷面板和金属背板对v50的影响，图10、11示出了φ7.62 mm子弹侵彻不同厚度比例的复合靶板结果，图12表明了装甲钢厚度是影响v50的主要因素。

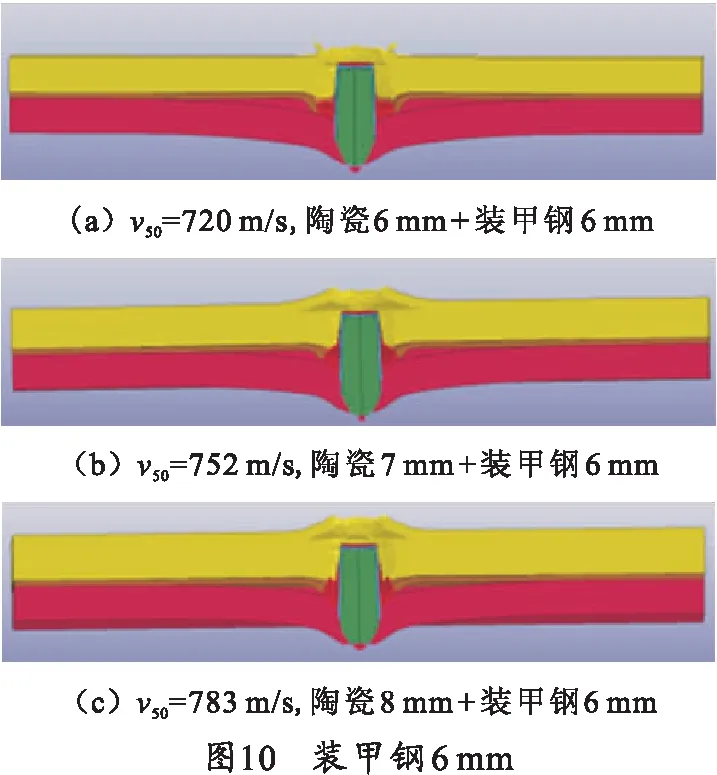
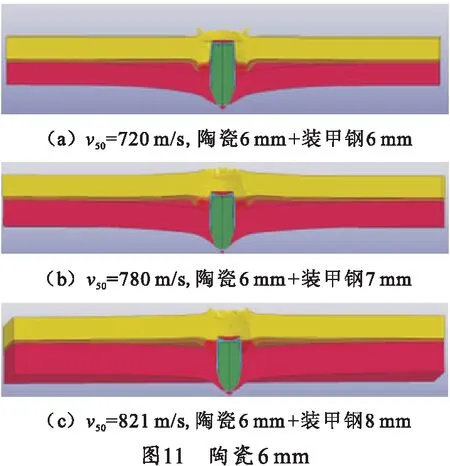
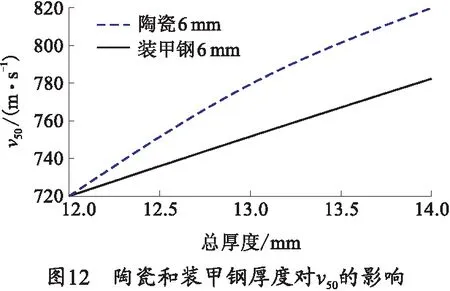
2.2 陶瓷锥角研究

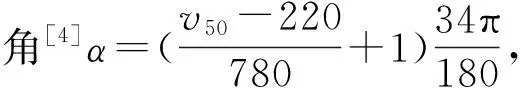
(10)

式中ρc为陶瓷密度。

图13表示了不同陶瓷厚度下陶瓷的破碎情况，图14为不同v50下陶瓷半锥角和陶瓷锥质量关系曲线。

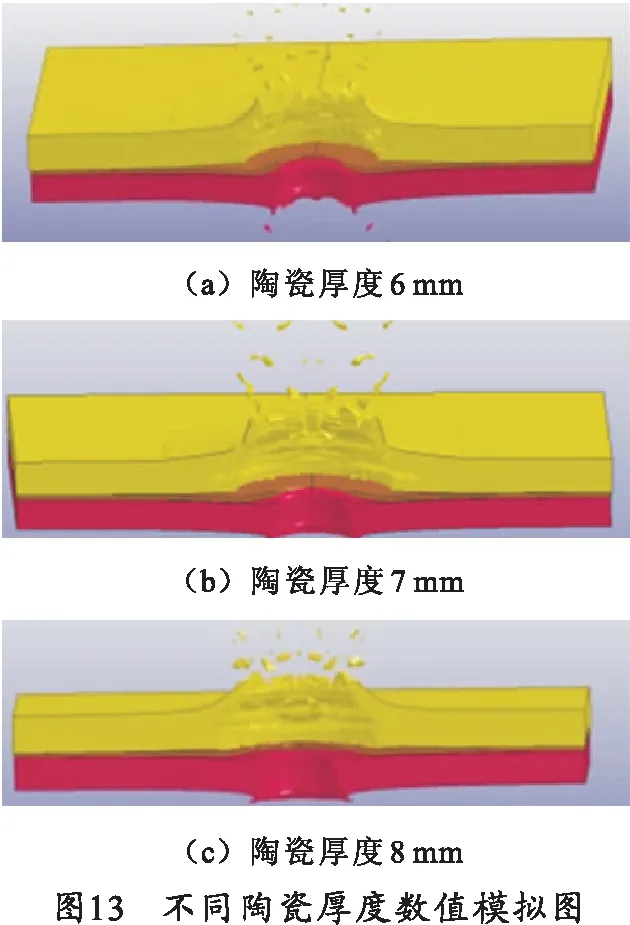
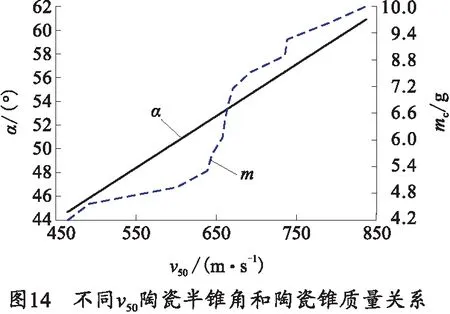
由图14可知陶瓷锥质量随初始速度的增加而增加，由牛顿第三定律，作用在弹芯的冲击压力大小与作用在陶瓷面板的压力大小相等，随着弹芯初始速度的增加，由式α计算公式[4]可得陶瓷锥角增大；同时由动量定理可知，作用在陶瓷面板的冲击压力增大，进而侵彻陶瓷面板的动能增加，综合式(10)可得陶瓷锥的质量增加。需说明的是笔者提出的理论模型是基于冲击压缩波在面板侧边界反射的先后差异不明显且可以形成较为完整的陶瓷锥情形，若冲击压缩波在面板侧边界反射的先后差异较大，形成的陶瓷破碎锥不完整或无法形成陶瓷锥[7]，则陶瓷锥消耗的能量减小，故推测v50会减小。

2.3 预测弹芯剩余高度

根据图1理论分析模型，预测弹芯剩余高度与弹道极限速度v50的关系，可将弹丸质量损失耗能表示为

(11)

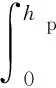
(12)

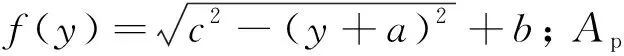
由于粘结层耗能占所有能量损失比例很小，可忽略不计。当质量损失发生在圆弧部时，弹芯质量损失所对应的高度h可从式(13)中解出：

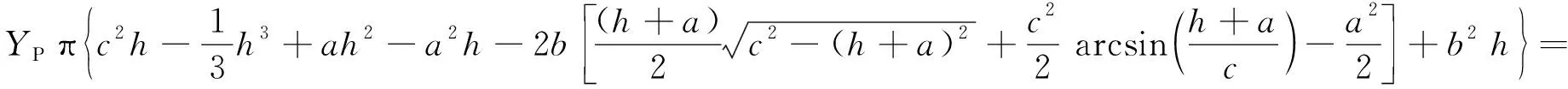
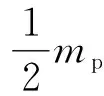
(13)

则弹芯剩余高度为

hr1=h0-h,

(14)

式中，h0为弹芯初始高度。

当质量损失发生在圆柱部时，弹芯质量损失对应的高度h：

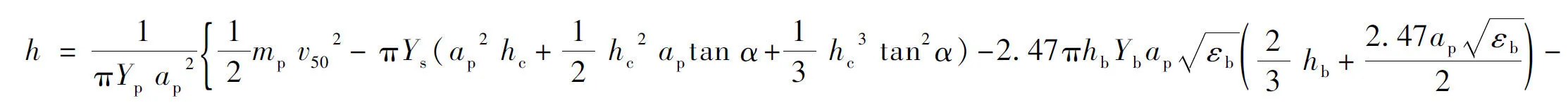
(15)

则弹芯剩余高度为

hr2=h0-h-hp.

(16)

将数值模拟、本文试验数据和理论计算得出的弹芯剩余高度进行对比，结合表2绘制出不同陶瓷靶板厚度下剩余弹芯厚度，如图15所示。

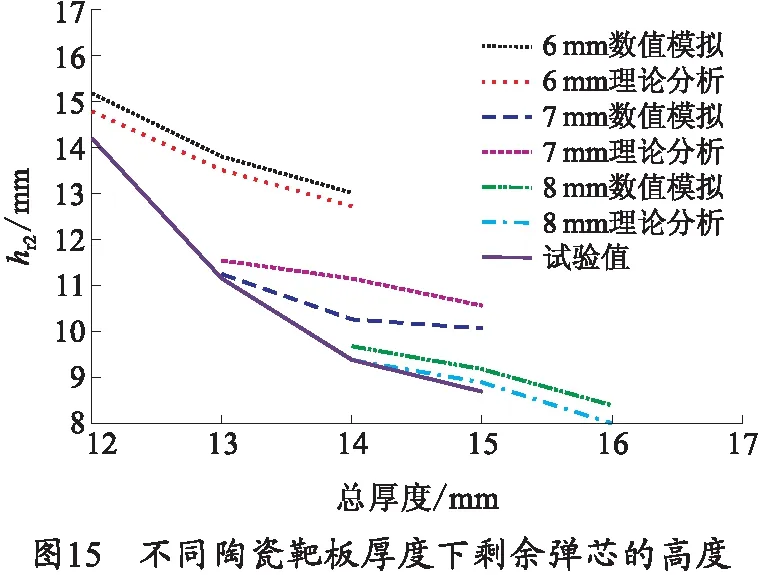
发现试验数据和数值模拟得出弹芯剩余高度与理论值误差在15%以内；随着极限速度的增加剩余高度越小的趋势一致，但有待更多的试验验证。同时发现陶瓷越厚，弹芯剩余高度越小；陶瓷厚度增加比金属背板厚度增加对弹芯剩余高度影响更大。分析其原因弹芯在击碎陶瓷面板时发生的界面击溃效应，导致的轴向侵蚀与径向断裂破坏，界面击溃过程中钢芯质量径向流动速度的增加导致径向薄片质量增加，且随着速度的增加这种现象越明显；弹芯在侵彻金属背板时，发生质量侵蚀变化较小[14]，则陶瓷厚度对弹芯剩余高度影响更大。对于弹芯剩余高度的预测有待更多试验的验证，弹芯的剩余高度预测对子弹的设计有重要参考意义。