火炮高平机电液伺服系统自适应动态面反演控制
2021-05-13宋卓异尹强聂守成赵飞
宋卓异,尹强,聂守成,赵飞
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.中国人民解放军63850部队,吉林 白城 137001)
高平机即为高低平衡机,是一种具有高低机和平衡机双重作用的机构[1],用于驱动火炮起落部分运动,赋予火炮高低射角和承受射击载荷[2-3]。目前用于大口径自行火炮的多为液体气压式高平机[1],其在电液系统的驱动下实现火炮的自动瞄准与人工操瞄。
高平机可以看作一种三腔结构的液压油缸,其与蓄能器相连的第三腔被称作平衡腔。相比两腔油缸而言,平衡腔的存在可以提供一个额外的平衡力,对大口径火炮起落部分质心前移、低射角时的冲击和跳动现象有较好的抑制作用,并能提升调炮到位精度,缩短调炮时间,但也使得运动过程中出现非平衡扰动,还提高了系统的复杂度。同时,高平机电液伺服系统本身还具有负载惯量大、存在参数不确定性和非匹配不确定性、工作环境复杂多变的特点[4],故较难实现快速高精度轨迹跟踪和位置控制。
近年来,动态面等控制方法被广泛应用在电液伺服系统中,文献[5]为克服大型起竖系统的非线性与不确定性,提出一种基于动态面的控制策略,提高了起竖系统的鲁棒性和稳定性。文献[6]针对液压四足机器人髋关节工作情况的复杂性和阀控缸自身的非线性,提出了一种鲁棒自适应动态面控制,通过仿真证明了算法的有效性。文献[7]针对火炮高平机电液系统存在强烈非线性及非匹配不确定性的问题,提出基于K观测器的动态面控制策略,成功解决了非匹配非确定这一类问题。文献[8]基于起竖机构模型提出了动态面自适应模糊滑模控制策略,数据表明该方法有较强的鲁棒性和良好的跟踪性能。
笔者建立了高平机电液伺服系统模型,根据模型特点提出了一种基于反演的自适应动态面非线性控制方法,反推控制律过程中引入自适应和动态面控制方法,并给出了稳定性证明,最后通过机电液联合仿真验证了控制策略的有效性。
1 高平机电液伺服系统建模
1.1 力矩平衡方程
某火炮高平机电液伺服系统主要由双高平机油缸、平衡阀、伺服比例阀、蓄能器、上架及摇架等组成。通过控制伺服比例阀的阀芯动作来进行流量控制,实现高平机油缸的伸出与收回,完成火炮起落部分的上行与下行动作。控制器比较实际角度信号与指令后输出控制量,控制身管到指定射角,高平机电液伺服系统工作原理如图1所示。 以耳轴中心O为原点,A点为高平机下耳轴与上架铰接点,B点为高平机上耳轴与摇架铰接点。设γ为火炮起落部分重心和原点的连线与身管轴线的夹角,α为OB与高平机轴线AB的夹角,β为OA与OB的夹角,θ为身管转动角度,OB=l1,原点与重心的连线距离为l2,OA=l3.
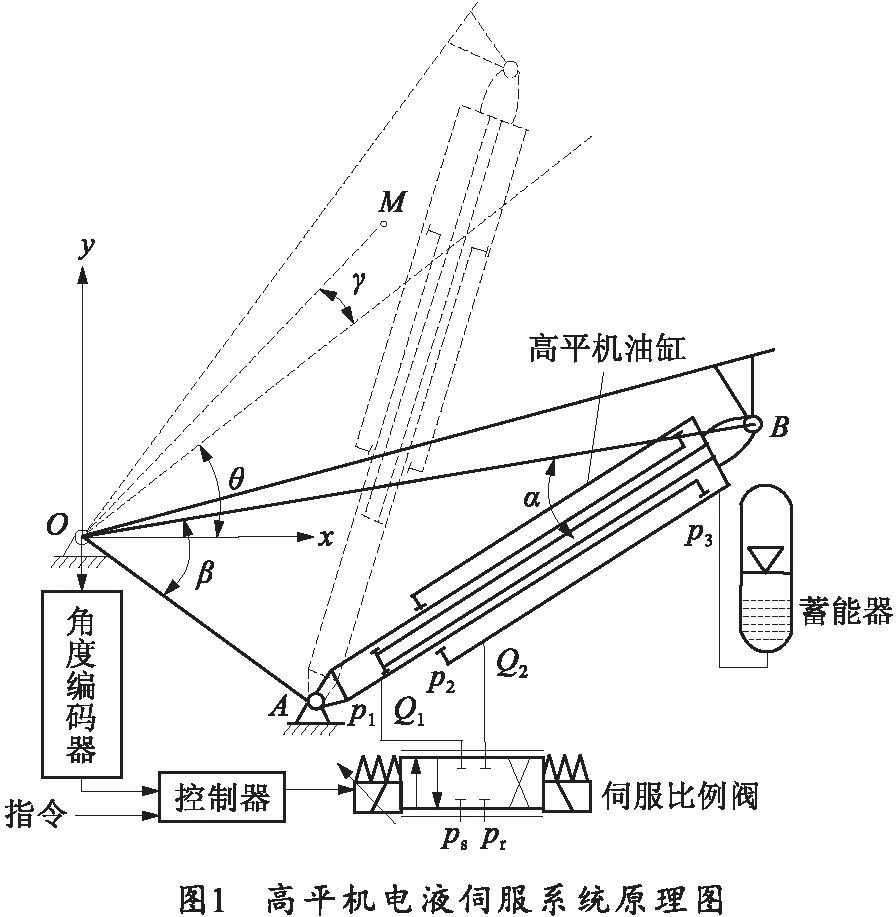
由三角函数正弦定理与余弦定理可得高平机驱动力臂:
(1)
系统惯性负载动力学方程如下:
(2)
式中:J为身管等效转动惯量;M为起落部分等效质量;g为重力加速度;B为阻尼系数;Td为扰动力矩;F=p1A1-p2A2+p3A3,p1,p2,p3分别为进油腔、回油腔及平衡腔的压力,A1,A2,A3分别为进油腔、回油腔及平衡腔的压力受力面积。
平衡腔压力可由波义耳定律表示[7]:
(3)
式中:p0为蓄能器充气压力;V0为蓄能器初始容积;Vc0为充液后气体容积;x为高平机位移;n=1.4.
1.2 伺服阀流量方程
控制量与阀芯位移的关系为
xv=καu,
(4)
式中:xv为阀芯位移;κα为伺服阀放大系数。
Q1s和Q2s分别为进入和流出阀流量,回油压力设为0,伺服比例阀流量方程表示为
(5)
(6)
式中:Cd为流量系数;ω为阀口面积梯度;ρ为油液密度;ps为系统压力。
对式(5)、(6)简化,则有:
(7)
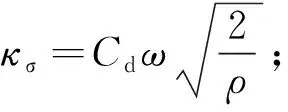
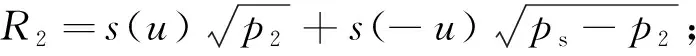
如果u≥0,s(u)=1;如果u<0,s(u)=0.
1.3 高平机油缸流量方程
设Q1为高平机进油腔流量,Q2为高平机回油腔流量,忽略管路膨胀和损失时,Q1与Q1s相等,Q2与Q2s相等,高平机连续流量方程为
(8)
式中:V1=V01+A1x,V01为油缸进油腔初始体积;V2=V02-A2x,V02为油缸回油腔初始体积;x为高平机位移;Ci为内泄漏系数;Ce为外泄漏系数;βe为液压油刚度。
根据数学模型设计状态变量
高平机电液伺服系统存在多个不确定参数,但油液弹性模量、液压油密度、高平机油缸初始体积等均可合理假设为已知固定值,同样,较少的未知参数可以简化控制器,但阻尼系数B和油缸内泄漏系数Ci较难获知,且随油缸伸出速度和位移而时变,对于执行器的控制影响较大[9]。故利用自适应量θ1和θ2对B和Ci进行估计,根据式(1)~(8)可得状态方程如下:
(9)
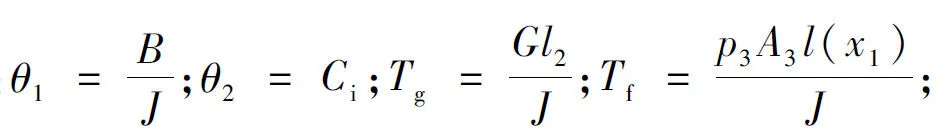
2 自适应动态面反演控制器
2.1 控制器设计
由于系统中存在的非匹配不确定性不能通过改变控制输入u来施加影响,故基于反演设计的方法设计非线性控制器。对式(9)的控制对象进行控制律设计,目的使理想角位移x1d与实际角位移x1的差值尽可能小,进行如下假设:
1)xi(i=1,2,3)均可采取,为系统状态实际值,xi及其导数连续有界;
2)x1d为期望的角度信号且三阶导数连续有界,x2d和x3d为虚拟控制量的期望值;
3)存在正实数D使得|d(t)|≤D.
(10)
定义3个系统误差变量如下:
(11)
式中:x1d为理想轨迹;x1为实测角度信号;e1为跟踪误差。
定义Lyapunov函数:
(12)
对式(12)求导得
(13)
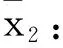
(14)
反演过程中对虚拟控制求导会出现微分膨胀,增大计算难度。利用一阶低通滤波器来计算虚拟控制的导数估计值可以避免微分膨胀[11]。设x2d为虚拟控制量的一阶低通滤波器输出,滤波器方程如下:
(15)
定义第2个Lyapunov函数:
(16)
对式(16)求导得
(17)
(18)
式中sgn(e2)为符号函数。
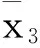
(19)
再定义第3个Lyapunov函数:
(20)
对式(20)进行求导得
(21)
此时,设计控制律u为
(22)
根据Lyapunov稳定性判据构造自适应律
(23)
式中γ1和γ2为自适应增益系数。
2.2 稳定性证明
对滤波器误差y2求导并由三角不等式得
(24)
(25)

(26)
同理可知存在一个正定连续函数B3:
(27)
使得
(28)
此时对V3求导并由不等式得
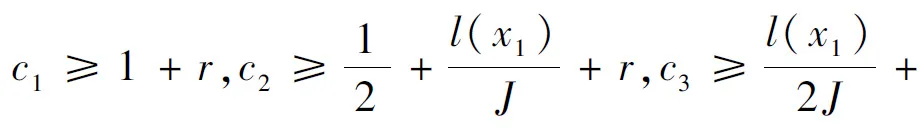
(29)
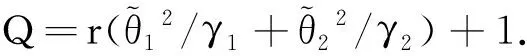
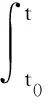
(30)
所以V3(t)是渐近收敛的。
3 联合仿真分析
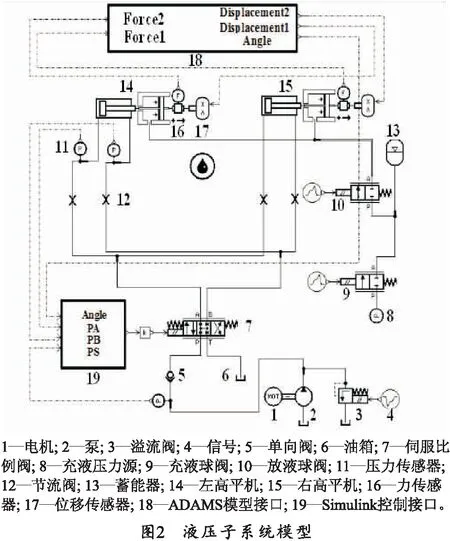
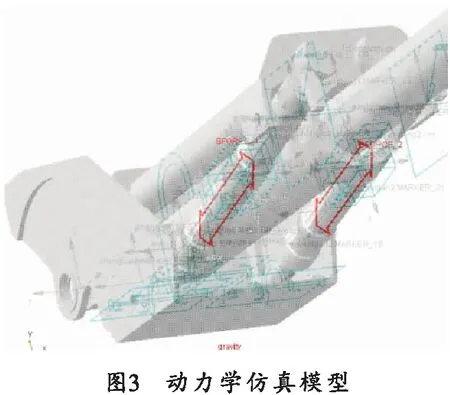
利用联合仿真检验算法的收敛性与有效性,在仿真软件AMESim中建立高平机液压子系统模型,如图2所示。系统压力设定为13 MPa,蓄能器充液压力8.7 MPa,充气压力2.2 MPa.设置高平机油缸的黏性摩擦系数、死区面积及泄漏系数。考虑到此机械系统响应频率远低于伺服阀且实际工程中多采用零遮盖、低滞环的伺服阀,所以忽略了伺服阀死区或滞环等影响。控制系统通过传感器采集实时身管角度、高平机A、B腔和系统压力。在机械系统仿真软件ADAMS中建立火炮起落部分、左右双高平机及上架模型,并定义运动副、约束、添加高平机油缸的摩擦阻力等,起落部分质量约为2 500 kg,如图3所示。根据所设计的算法在Simulink中建立控制系统并借助接口技术实现机电液系统联合仿真,算法求解器采用固定步长的Ode3,液压和机械系统采用各软件默认求解器,仿真时间为14 s.
所设计的理想曲线为梯形速度曲线,0—2.5 s身管保持0°射角不变,2.5 s时火炮起落部分上行,经4.69 s至60°射角,9 s时下行,经2.69 s至30°射角。在零初始条件下,用笔者所设计的自适应动态面反演算法(BADSC)、普通动态面算法(BDSC)及PID算法进行对比分析,图4为3种算法下的角度曲线对比图,均能实现火炮指定射角的路径跟踪瞄准,图5为3种算法下的跟踪误差曲线对比图。
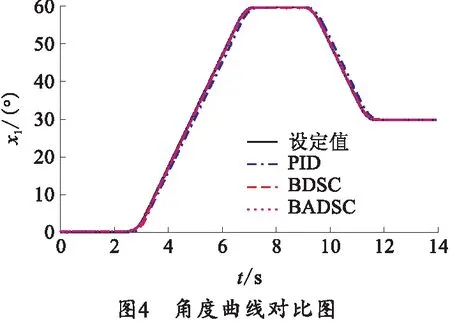
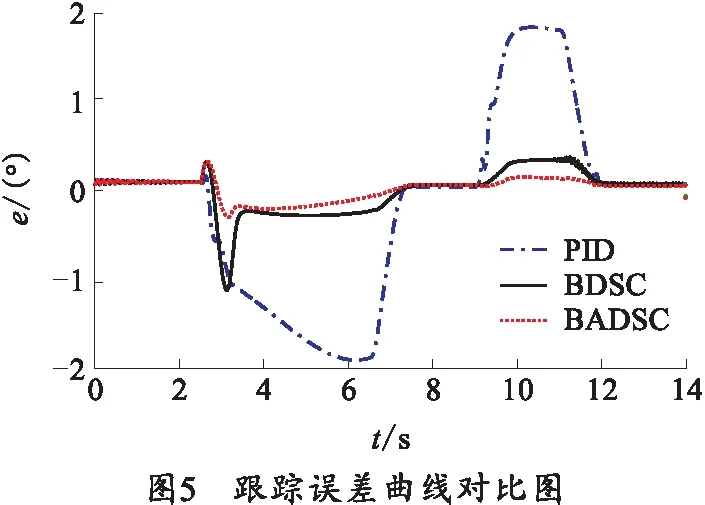
从图4和5中可以看出BADSC的跟踪性能明显优于PID算法和BDSC,身管上升时最大跟踪误差出现在初始阶段为0.371 4°,保持在60°射角的稳态误差为0.006 5°,身管下降时最大跟踪误差在0.08°左右。对于PID控制算法,身管上升时最大跟踪误差为1.977 1°,保持在60°射角的稳态误差为0.024 7°,身管下降时最大跟踪误差在1.769 2°左右。对于普通动态面控制算法,身管上升时最大跟踪误差出现在1.183 5°左右,保持在60°射角的稳态误差在0.009°左右,身管下降时最大跟踪误差在0.306 9°.图5中可看出未知参数估计的变化对控制效果有一定影响,相比BADSC算法,未知参数固定的BDSC算法不仅提高了动态误差和到位误差,还使得油缸下行时出现了抖振现象。
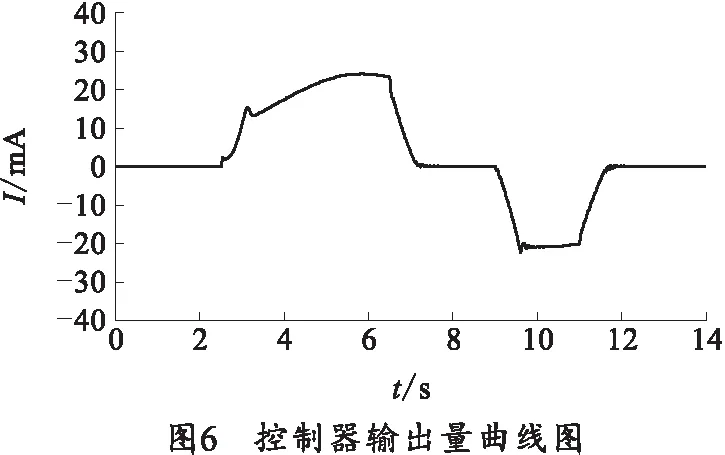

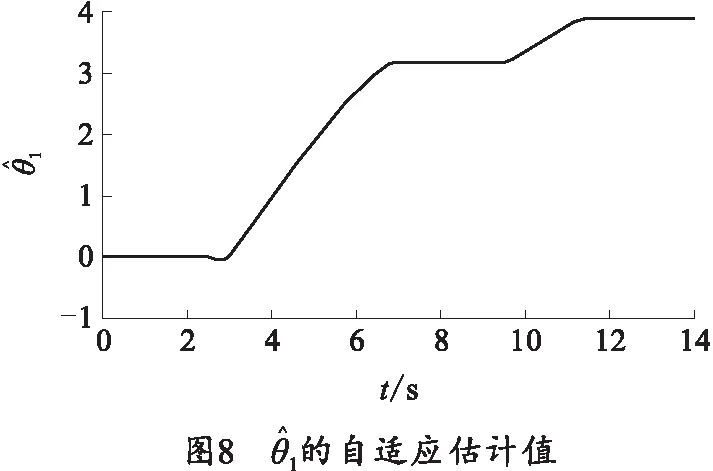
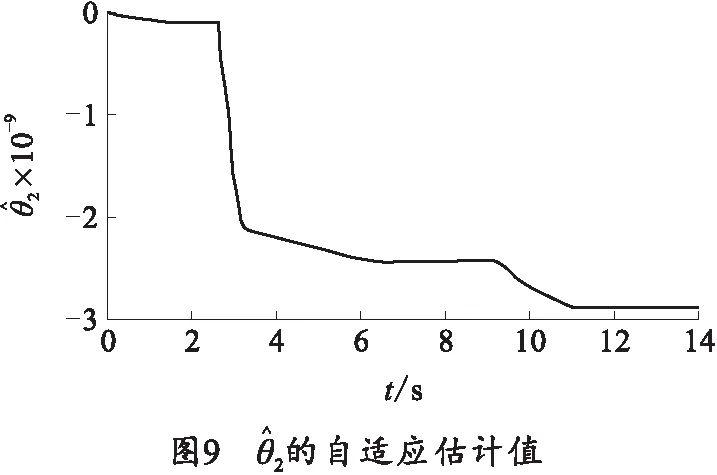
4 结束语
高平机电液伺服系统是复杂的机电液一体化系统,笔者较为全面地建立了此系统的非线性数学模型、ADAMS动力学仿真模型、AMESim液压系统系统模型,基于模型建立机电液一体化仿真平台,对此类系统的建模与仿真有较好的参考意义。
针对高平机电液伺服系统存在的负载大惯量、非匹配不确定性、参数不确定性、非平衡扰动及外部扰动等问题,提出了一种自适应动态面反演控制方法,利用反演解决非匹配性问题,通过动态面控制方法消除微分膨胀,设计自适应律在线调整高平机油缸内泄漏系数和阻尼系数,并将自适应律与虚拟控制量结合,简化控制器设计流程。联合仿真验证该控制方法有较高的跟踪精度和较小的稳态误差,并能够保证火炮起落部分快速上下行时的平稳性,具有一定的应用前景。
