舰炮整体振动分析及结构参数优化研究

刁诗靖，赵洋，彭京徽

(海军工程大学 兵器工程学院，湖北 武汉 430033)

舰炮作为一类常规武器，打得准、打的远是体现其作战使用性能的重要指标。打得准就要保证其射击精度，减小振动带来的影响；打的远则需要有足够的高温高压火药气体的作用，但在巨大的炮膛合力作用下，必将给舰炮系统产生振动现象，影响其射击精度并加速相关部件的损坏，降低可靠性。舰炮系统的振动不仅与射击时的火药载荷有关[1]，其本身的结构参数对振动也有重要的影响。在舰炮战术指标确定的情况下，通过修改其结构参数，便成了降低舰炮振动的重要手段[2]。

为了解决舰炮系统振动现象带来的一系列问题，已有许多专家学者对此展开了研究[3-24]。在常见的舰炮系统振动的研究中，普遍通过建立系统整体动力学运动方程、建模仿真和局部优化设计等几种方式展开研究。如王凯等[6]以多柔体动力学理论为基础，通过建立某舰炮刚柔耦合模型，进行刚柔耦合多体发射动力学仿真，对比得到了炮口振动情况和一系列的动力特性曲线；王德石等[7]在研究火炮振动对射击精度的影响时，利用火炮动力学的Lagrange方程及Gauss变分建模方法，并由其建立了火炮整体振动的刚性、刚柔耦合多体系统模型，获得了火炮振动与其结构参数的内在联系；王宝元等[8]从局部着手研究了不同身管膛线类型产生的振动响应对火炮射击密集度性能的影响。在上述基于对称条件下简化的平面内力系来进行动力学计算和建模仿真研究，都忽略了弹丸作用于膛线导转侧的力矩带来的纵向翻转，对舰炮系统整体在弹丸出膛时的静止性和稳定性条件以及横向跳角运动微分方程也鲜有研究。

笔者基于简化的三自由度舰炮与平台系统的振动模型,对发射过程中的舰炮系统整体振动及其静止性和稳定性进行了研究，并以某型舰炮为例，采用遗传算法进行了结构参数优化设计，为舰炮结构设计和优化设计提供了可行的方法。

1 简化模型与运动方程

舰炮系统是一个复杂的多体运动，为了便于研究舰炮系统的整体振动，在水平射角时将其简化为如图1所示的力学模型。其中，把舰艇甲板看作固定平面，舰炮与甲板通过螺栓和基座等连接，由于螺栓和基座具有一定的弹性和刚度，可将其看成是弹簧阻尼系统，且分别位于横向内力系平面的支点A、B和过质心垂直于横向内力系的纵向平面力系上的支点C、D.图1中Ki、Ci分别为弹簧的刚度和阻尼器的阻尼，m为舰炮系统的质量，Li为各支点到质心所在轴线的距离。

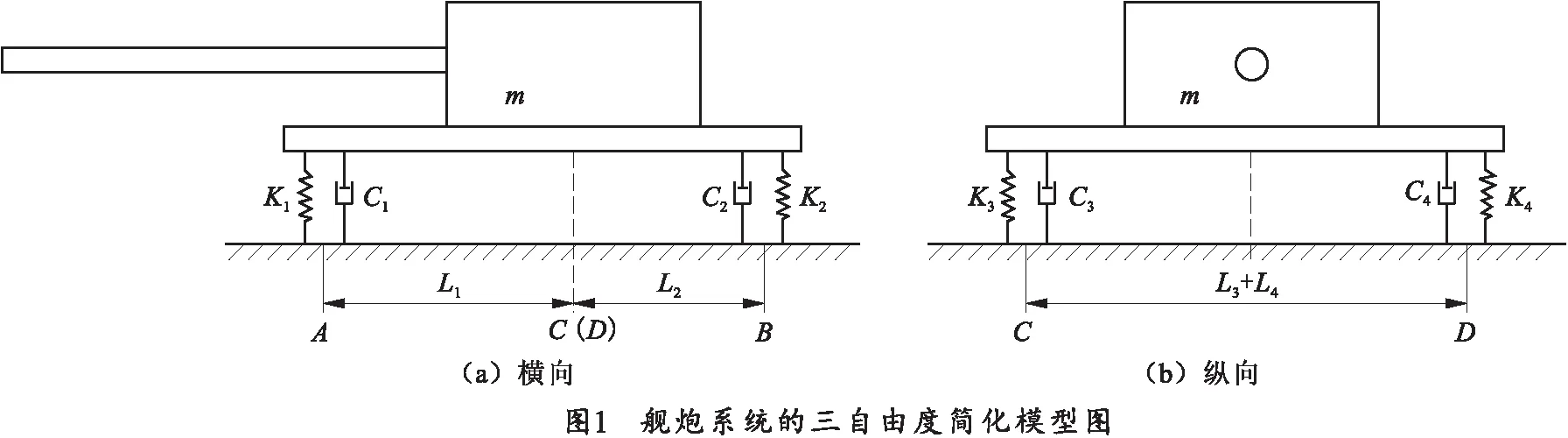
以舰炮质心的竖直位移y、绕质心的横向转角θ和由导转侧力矩M对C(D)产生纵向转角φ为坐标，坐标原点取在静平衡位置，此时舰炮重力与舰艇甲板支撑力是一对平衡力。对上述简化的三自由度舰炮力学系统建立动力学运动微分方程，得到用矩阵和向量表示式:

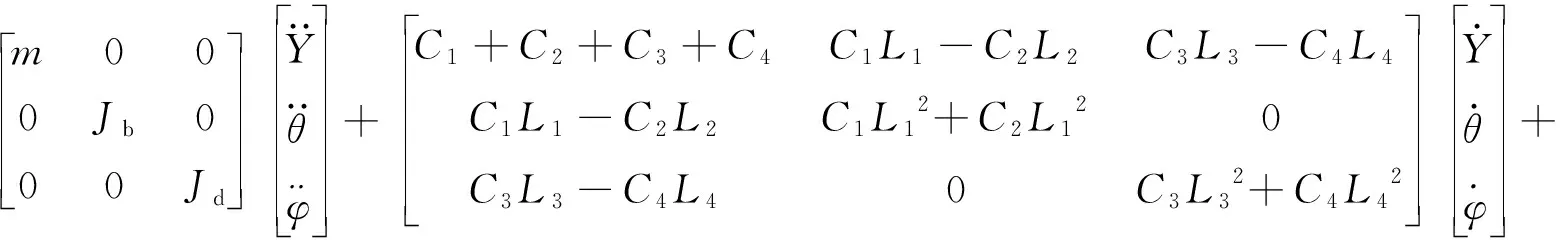
(1)

式中：Jb为舰炮系统的横向转动惯量；Jd为舰炮系统的纵向转动惯量。

如果4个支点处的弹簧阻尼系统相同，即C1=C2=C3=C4=c，K1=K2=K3=K4=k，另外，由于舰炮简化系统的轴对称性，所以L3=L4，式(1)可进一步化简为

(2)

由简化后式(2)和原式(1)可知，支点C、D处的弹簧阻尼系统不仅仅影响着舰炮系统整体纵向振动，也影响着系统的横向振动。

2 系统的固有振动特性

在选定的物理坐标条件u下，三自由度无阻尼系统的简谐自由振动应满足下述微分方程及其初始条件。

(3)

(4)

式中：φ表示振幅的三维向量;α是振动初始角;ω为舰炮振动频率。

把式(3)、(4)代入式(2)，欲使其在任意时刻都成立必有如下关系：

(K-ω2M)φ=0，

(5)

即：

(6)

三自由度系统中系统矩阵是对称矩阵。欲使系统振动，则应有非零解，且满足：

(7)

展开行列式可得关于ω2的二次代数方程，解得3个非负实根ω12、ω22、ω32：

(8)

进而求得ω12、ω22、ω32的非负平方根ω1、ω2、ω3，并从小到大的依次称为第一阶固有频率、第二阶固有频率和第三阶固有频率。同时，由上述推导过程及求解结果可知，系统的固有频率互异，其所对应的固有振型关于质量矩阵、刚度矩阵加权正交，表明无阻尼系统各阶固有振动间的能量是不耦合的，根据这一特性可简化系统振动的求解过程。

已知固有频率ωi，可利用无阻尼固有频率和有阻尼固有频率的关系，求出三自由度粘性欠阻尼系统的振动响应的有阻尼固有频率ωd：

(9)

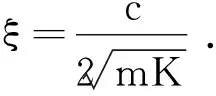
3 舰炮系统射击静止性和稳定性

为了研究舰炮系统整体振动对射击精度的影响，所以仅考虑弹丸在膛内运动0～tg这一时期，特别是当t=tg时，产生最大横向转角θ(tg)，导转侧力矩Mφ，纵向转角χ=χmax，由于后坐运动导致的质心下移最大距离y(tg)，后移最大距离记X(tg)，得到图2所示的系统简化图。

保证舰炮在水平方向的静止性条件，甲板对回转装置产生水平反力FT与后坐阻力FR应是一对平衡力，且满足：

FRcos(θ+φ)≤FR≤FRmax≤[FT],

式中，φ为射角;水平反力FT由螺栓组提供，且[FT]=nKsA[τ],n为螺栓的数量,Ks为与螺栓布置位置相关的安全系数[19],A为螺栓的最小横截面积,[τ]为螺栓的许用剪应力。

要知道舰炮的起跳趋势ΔhA，需计算出舰炮系统绕支点B的后坐颠覆力矩MB，具体求法可参考文献[9]。在弹丸射出瞬间高压气体给舰炮的力仍然可以看作是系统内力，由于后坐运动导致系统质心的改变，但质心下移距离y(t)不会导致弹簧阻尼系统平衡位置的改变，造成弹簧阻尼系统平衡位置的改变的原因在于质心后移距离X(t).

由舰炮系统设计可计算得到质心下移运动方程y(t)[21]，进而求得横向转角的运动方程：

(10)

求解式(10)，可由初始条件求得

(11)

(12)

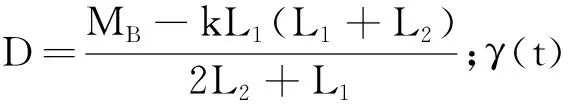
因为限制和减小舰炮的最大起跳实际就是减小最大跳角γ(tg)的大小，所以对舰炮系统的结构参数进行合理优化有助于减小舰炮系统整体的最大跳角γ(tg)，以减小舰炮射击时的整体振动。

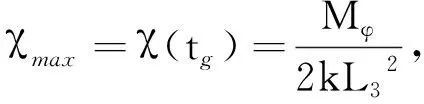
(13)

式中Mφ与弹丸转速、线膛等相关，可由舰炮系统设计得到。

4 舰炮结构参数优化设计

4.1 舰炮受力分析与运动方程

对舰炮后坐时期后坐部分及整炮进行受力分析并建立运动方程，受力如图3、4所示。

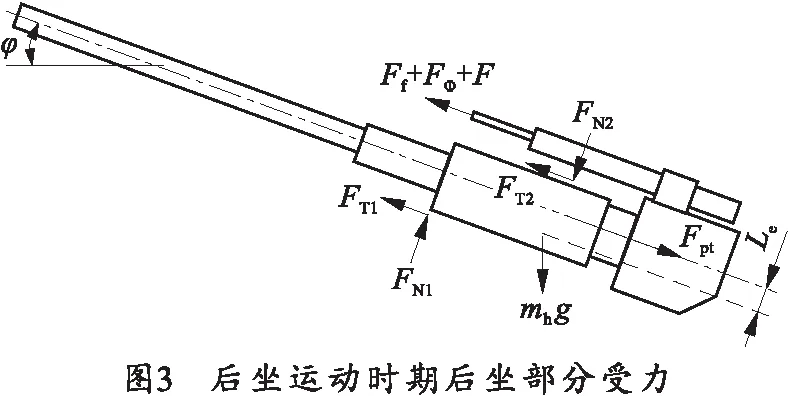
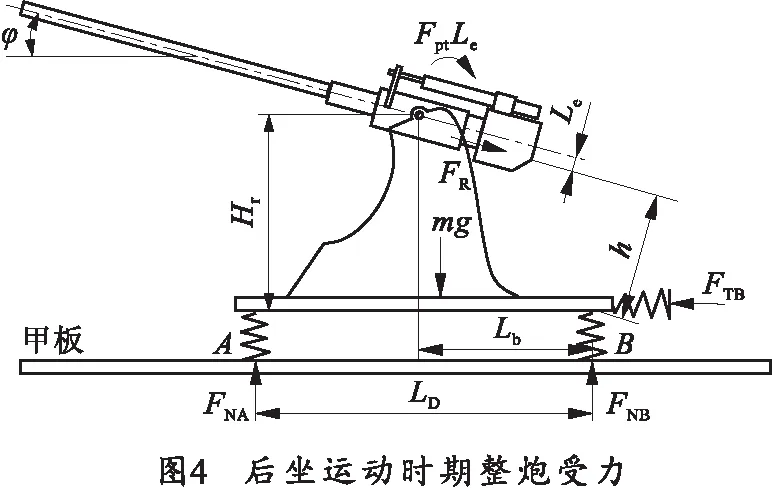
取顺时针为力矩正向，建立受力方程其中，Fpt为炮膛合力;LD为前支点A到后支点B的距离；Fφ为驻退机力;Ff为复进机力;φ为俯仰角;FR为后坐阻力；Hr为耳轴中心到甲板的高度；Lb为耳轴中心到后支点B的水平距离；Le为耳轴中心到后坐部分质心运动轨迹的距离；mh为后坐部分质量;x为后坐位移。可得静平衡位置上的3个约束反力：

(14)

式中：FR′=-FR；h=Hrcosφ-Lbsinφ+Ld.

对舰炮复进运动时期后坐部分进行受力分析并建立运动方程，如图5所示。

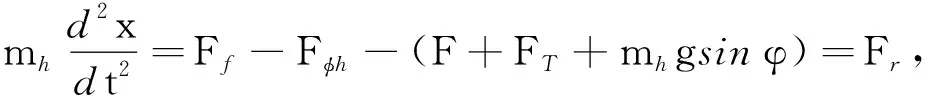
式中:Fφh为复进液压阻力;Fr称为复进合力，其大小和正负表示复进运动加速度的大小和方向,当Fr>0时，为复进加速时期,Fr<0时，为复进减速时期。

以整炮为研究对象，复进加速时整炮的受力分析如图6所示。

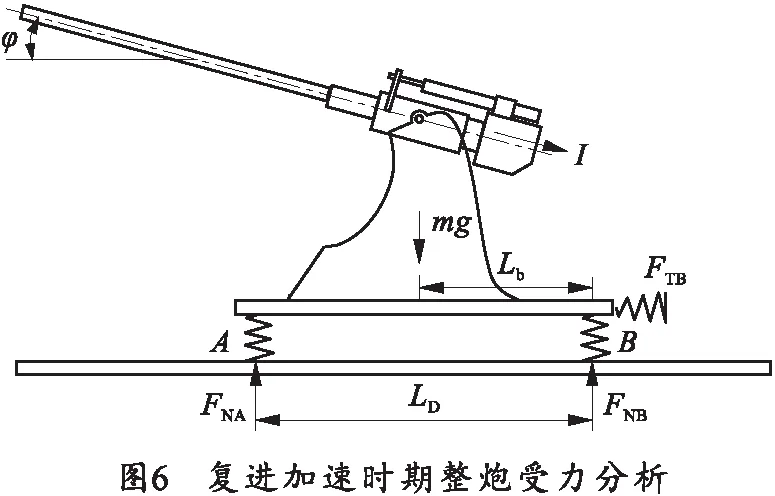
通过整炮的受力分析可以看出，复进加速时期的受力状态与后坐惯性时期的受力状态相同，只是过后坐部分质心的力由后坐阻力FR换成了复进合力Fr,显然FR≫Fr，因此只需保证舰炮后坐时期静止性和稳定性条件，就能够保证复进加速时期舰炮的静止性和稳定性条件。

以整炮为研究对象，复进减速时整炮受力分析如图7所示。

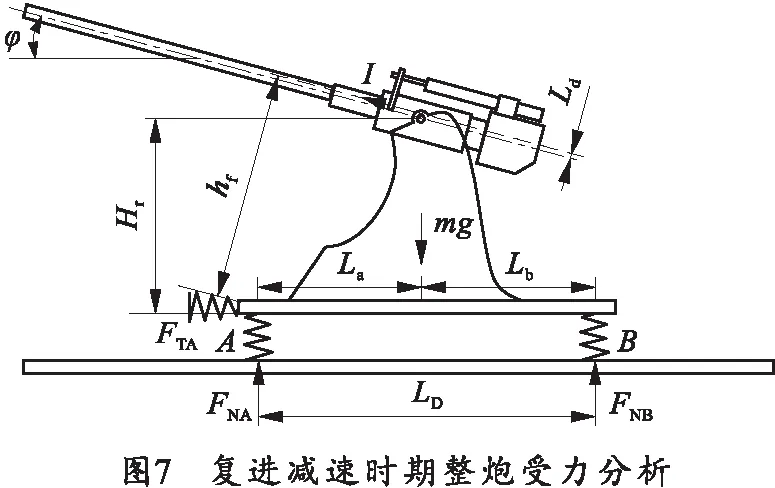
图中La为耳轴中心到后支点A的水平距离；Ld为耳轴中心到后坐部分质心运动轨迹间的距离，耳轴在下为正。

复进减速时期的受力状态与后坐时期、复进加速时期不同。以A为坐标原点，炮口指向炮尾的水平方向为正x方向，竖直向上为正y方向，顺时针方向为力矩正方向。可得到约束反力的表达式：

(15)

式中：λ为复进位移；hf为作用在后坐部分质心的惯性力到前支点A的距离。

4.2 舰炮结构参数的优化设计

在舰炮设计中，需要同时使得颠覆力矩和甲板受力最小，该问题属于多目标优化问题。为了合理设计各个结构参数，使用基于遗传算法和非线性规划的函数寻优算法。经典非线性规划算法大多采用梯度下降的方法求解，局部搜索能力强，但是全局搜索能力弱。遗传算法采用选择、交叉和变异算子进行搜索，全局搜索能力强，但是局部搜索能力弱，一般只能得到问题的次优解，而不是最优解[17]。因此，笔者将两种算法的优点结合起来，一方面采用遗传算法进行全局搜索；一方面采用非线性规划算法进行局部搜索，以在规定的参数设计范围内，求解各个参数的最优解。

后坐运动时期舰炮所受颠覆力矩表达式为

M=FptLe+FR(Hrcosφ-Lbsinφ+Ld)+mhgx.

(16)

参考某型舰炮的结构参数，建立优化数学模型如下：

(17)

待优化的结构参数取值范围为：1 m≤Lb≤2 m，-0.02 m≤Le≤0.02 m，2 m≤LD≤4 m，2 m≤Hr≤3 m，-0.02 m≤Ld≤0.02 m.

遗传算法参数设置为：种群规模200，进化次数50次，交叉概率0.6，变异概率0.1，优化后的结构参数为：Le=5 mm，Hr=2.3 m，Ld=-0.5 mm，Lb=1.7 m，LD=2 m.Hr较优化前减小，Lb、LD较优化前增大，Le、Ld绝对值较优化前增大。计算优化前后颠覆力矩M和整炮前后支点受力FNA、FNB，结果如图8所示。

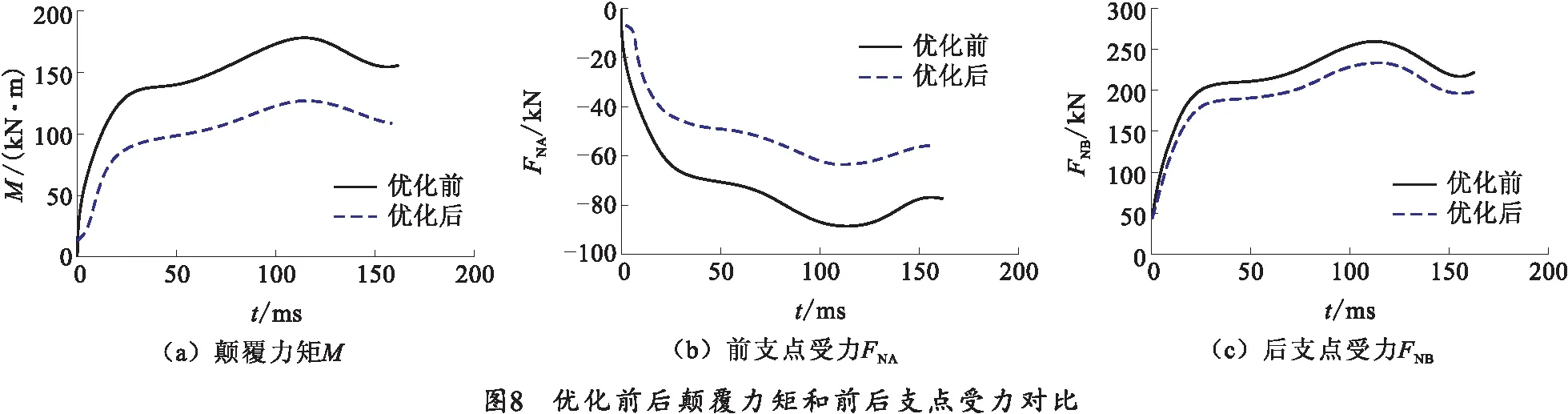
从图8可以看出，各个结构参数的取值对M、FNA和FNB的幅值有重要影响，结构参数经过优化后，M、FNA的幅值减小约25%，FNB的幅值减小约15%.

复进加速时期整炮和甲板的受力状态与后坐时期相同，故只需考虑复进减速时期的优化模型。建立复进减速时期优化数学模型如下：

(18)

待优化的结构参数取值范围为：2 m≤Hr≤3 m,2 m≤LD≤4 m,-0.01 m≤Ld≤0.01 m,1 m≤La≤2 m.

优化后的结构参数为：Hr=2.25 m，Ld=-0.5 mm，La=1.25 m，LD=2 m.Hr较优化前减小，La、LD较优化前增大，Ld绝对值较优化前增大。分别用复进减速时期优化取值和后坐运动时期优化取值计算复进运动时期颠覆力矩Mf和整炮前后支点受力FNA、FNB，结果如图9所示。

从图9可知，在复进运动时期，采用复进减速时期参数优化结果时，前支点受力FNA幅值减小约20%，颠覆力矩Mf和后支点受力FNB差别较小。但考虑到后坐时期整炮受力大于复进时期，为保证后坐运动时期舰炮处于最佳受力状态，复进时期的结构参数选取仍要以后坐时期优化结果为准。

5 舰炮振动优化分析

从式(10)～(13)可以看出，舰炮系统的振动方程与舰炮质量、转动惯量、结构尺寸、外激励力以及舰炮与甲板之间约束的刚度和阻尼有关，舰炮的振动响应也是这些参数的函数。将第4节优化求得的结构参数和优化前的参数分别代入式(10)～(13)进行仿真计算，求得后坐和复进运动时期系统振动响应，结果如图10、11所示。从图10中可以看出，在炮膛合力和后坐阻力不变的条件下，在后坐运动时期，采用优化后的结构参数后，舰炮质心位移和速度减小20%以上；俯仰角度和角速度减小约80%.从图11中可以看出，在复进运动时期，采用优化后的结构参数后，舰炮质心位移减小约25%，质心速度减小60%以上；俯仰角度减小约5%，角速度减小约30%.

案例表明，在炮膛合力和后坐阻力不变的条件下，通过优化舰炮结构参数，舰炮振动响应减小20%以上。根据射击稳定性条件优化舰炮双面约束的约束力，是降低舰炮振动响应的有效手段，是反后坐装置设计以及舰炮结构设计的重要理论依据。

6 结论

通过简化的三自由度舰炮与平台系统振动模型，建立三自由度系统下的运动动力学微分方程，分析了系统的固有振动特性，并对舰炮射击时的系统受力和稳定性条件进行了研究。结果表明：

1)舰炮系统整体振动不仅与横向简化平面力系相关，也与纵向平面力系相关。

2)对所建立的三自由模型求解固有频率可知，其固有频率互异，其所对应的固有振型关于质量矩阵、刚度矩阵加权正交，表明无阻尼系统各阶固有振动间的能量是不耦合的。

3)通过建立相关方程与关系式可以求得系统的横向跳角和纵向转角的运动方程，由对弹丸出膛瞬间的系统稳定性可知，对舰炮结构参数进行合理优化都有助于减小舰炮系统整体的最大跳角γ(tg)和最大转角χ(tg)，从而减小舰炮振动。

4)通过选取某型舰炮案例进行静止性和稳定性分析，以平台对于舰炮的约束力为目标函数，对结构参数进行优化，能够有效降低舰炮的振动响应，为舰炮结构设计提供了理论依据。由于简化模型和实际舰炮的差异，所以具体的影响程度仍有待于试验的进一步验证。