不同土壤硬度对火箭炮发射初始扰动的影响研究

2021-05-13孙志群李强刘朋展许桎樟李先进

火炮发射与控制学报 2021年1期

孙志群，李强，刘朋展，许桎樟，李先进

(1.中北大学机电工程学院，山西太原 030051；2.武汉高德红外股份有限公司，湖北武汉 430070;3.75180部队，广西桂林 541000)

火箭炮是一种提供大面积瞬时密集火力的战术武器，由于其具有发射速度快、弹着覆盖面积大、火力猛、密度大、机动性好、作战效能高、造价低廉等特点，几十年来一直受到各国军队的青睐[1]。射击精度是衡量火箭炮性能优劣的重要指标，且炮口在射击时的初始扰动是制约射击精度的重要因素之一，炮口的初始扰动常常作为火箭武器射击精度评价的重要参考[2]。随着以Wittenburg，Schiehlen及Kane等多位学者研究内容为基础建立的多刚体动力学理论的发展，国内外研究人员将其应用到火箭炮系统发射动力学的研究中。实践证明，其对于一般刚体的计算精度较高，但不适用于不能完全处理为刚体的长板、细桶形等具有大形变的部件[3-4]，因此，研究刚柔耦合系统动力学具有越来越重要的意义。柔性体研究多采用Reyleigh-Rite法、有限元法、模态分析法等，Eberhard结合了柔性体有限元法和多刚体法的优点，以此为基础建立刚柔耦合动力学[3]。目前，火箭炮武器研究利用刚柔耦合取得了一系列成果，如引入碰撞模型和柔性发射管模型，研究火箭炮发射时定向钮的受力情况，或者通过建立刚柔耦合模型，并引入随机路面谱，研究行驶过程中火箭炮关键部件受力及振动特性[5-6]。目前的文献中多数考虑发射机构间的刚柔耦合，文献[7]考虑轮胎和土壤变形、滑移率、软土下轮胎滚动接近角和离去角等因素,建立轮-土模型并计算行驶过程中火炮发射的炮口振动特性，但其模型主要关注车轮的力学特征，弱化了土壤特性。文献[8]通过建立全炮柔性模型，以陆基发射方式，分析了考虑土体情况下发射系统的动力学特性，但其未考虑土壤内摩擦角、粘聚力等土壤特性，未能建立完整的土壤模型。以上文献也没有考虑土壤硬度对于火箭炮初始扰动的影响。

笔者研究对象为某轻型火箭炮，为了掌握火箭炮土基发射时的土壤形变特性，基于土动力学，建立柔性土壤模型；为了考虑火箭炮发射时，土壤刚度对于火箭炮初始扰动的影响，构建了采用刚柔耦合的土-架发射模型；通过土动力学分析实验，测定火箭炮支腿受力及炮口振动特性验证了土壤建模的正确性；通过改变土壤硬度，在高低80°、方向0°射角的炮口振动进行仿真计算，与试验测试数据对比，验证了精确度；并对发射时火箭弹的初始扰动进行计算，为土基发射的模型建模、分析及发射土壤硬度选择提供了有益指导。

1 全炮模型的建立

火箭炮发射系统的结构复杂，零部件众多，在保证不影响计算精度的前提下对其进行简化，以提高计算效率。具体的模型处理包括以下几个方面:将火箭炮左右发射箱与高低机合并为一体；忽略瞄准器具和方向机，高低机保留高低齿轮、齿弧；将耳轴与发射架合并为一体，与耳轴连接的轴承简化为圆环柱体；由于火箭炮发射部分刚度远大于土壤刚度，故作刚性处理；定向器与火箭弹建立准确碰撞模型，以使火箭弹运动与实际相符；将无限的大地简化为3个大型的土块，分别与两个前支腿和一个后支腿作用。模型示意如图1所示。

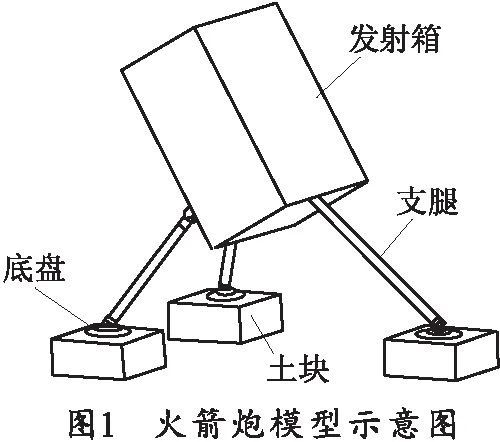
1.1 火箭炮刚柔耦合模型建立

将柔性体的分析结果与多刚体研究方法相结合，得到刚柔耦合动力学方程[9]。利用拉格朗日乘子法建立的系统刚柔耦合动力学方程为

(1)

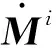
动力学中各零部件的约束关系主要通过关节连接(Joints)和接触关系(Contacts)来实现，通过合理的定义各零部件间的连接关系，使所建立模型与发射实际情况相吻合。各构件之间建立约束关系：

1)定向器与发射箱之间的约束。定向器与发射箱在装配中用卡扣锁死，限制定向器与发射箱无相对移动、无相对转动，且在模型中不考虑由于定向管与发射箱之间的微小间隙所产生的影响，故在仿真模型中，定向器与发射箱采用固定副连接。

2)发射箱与高低机之间的约束。发射箱与高低机之间设置一个绕耳轴转动的旋转副，并在旋转副上设置一个具有结构阻尼的扭簧等效高低方向的受力，扭簧的扭转刚度系数K为13.5 kNm/(°)[10].

3)支腿与大架之间的约束。3条支腿采用螺栓固定在大架上，在仿真模型中设置为固定副连接，支腿与地钎底盘采用固定连接，通过测量固定铰3个坐标轴方向的受力，可求解支腿受力。

4) 地钎与土壤的约束。由于单个地钎在土壤中的楔紧力很小，不足以稳定发射装置，故可忽略其楔紧力。模型中每个底盘采用3个不同方向地钎打入土壤，利用3个地钎不同方向的受力将每个底盘固定，所以土壤与地钎做接触处理。

1.2 弹管碰撞模型的建立

射击时，火箭弹直接与火箭炮定向器接触，而火箭弹在发射过程中，由于火箭弹定心部与定向器管壁的相互作用、弹管间隙等因素使得火箭弹在定向器中的运动特性相当复杂，已有文献[11]通过研究模型中的碰撞刚度与阻尼因数，可以以仿真的方式获得一般实验难以测到的火箭弹在管内复杂运动情况。火箭弹滑离参数(火箭弹线速度、火箭弹角速度、火箭弹低头角)是初始扰动计算的必要内容，所以有必要建立定向器与弹体碰撞模型，确定准确的滑离参数计算。笔者基于Hertz接触模型和多体动力学理论建立与实际情况基本相同的弹-管动力学模型。

接触碰撞通常采用非线性弹簧-阻尼模型进行计算，两物体发生碰撞的判断条件为是否产生穿透，当穿透量小于0时，两物体间的碰撞力0，否则碰撞力正。碰撞力的定义[11]如下：

(2)

式中：k为碰撞表面的刚度；e为弹性系数；δi为穿透力量；cmax为最大阻尼系数；δmax为最大穿透量。k可由以Hertz定律为理论基础的刚度计算公式给出：

(3)

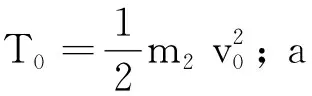
由于定向器和火箭弹定心部存在曲率，其碰撞接触相当于球体和球体的接触，a可表示为

(4)

式中：E1和E2，R1和R2，u1和u2分别表示定向器与火箭弹定心部的弹性模量、半径、泊松比。

由于弹管间隙远小于火箭弹定心部半径，且定向管与发射箱固联，质量远大于火箭弹，所以有以下关系成立，定向管与火箭弹的碰撞刚度为

(5)

碰撞接触的最大渗透量可表示为

(6)

将式(4)、(5)代入式(6)可得两者的最大渗透量：

(7)

1.3 土壤模型建立

在陆基发射环境下，土壤对于武器发射时部件受力响应具有重要的影响，部分研究将土壤采用弹簧或Bekker简化模型近似。但土壤在加载或卸载过程中，应力与应变之间表现有复杂的静压屈服、硬软化及剪切膨胀性等特性，弹簧模型不能表现土壤各种特性，Bekker简化模型虽然给出了土壤沉陷量与受压的关系，但并未解决土壤的剪切特性，与实际土壤模型仍有差距。

为了更好地描述土壤各项特性，研究土壤时采用其本构模型。在土力学中，常用的可以准确描述这类材料的强度准则为Drucker-Prager屈服准则，其是对Mohr-Coulomb准则的近似，用以修正Von Mises表达式中包含一个附加项，其屈服强度随着侧限压力的增加而相应的增加，其塑性行为被假定为理想弹塑性[12]。模型在子午面上的屈服面形状为圆形，使得模型在数值计算中效率较高且易于收敛，且模型在子午面上的屈服面形状可以用线性函数、指数函数等形式进行模拟，具有较强的适应性。

土壤DP模型等效应力公式为[13]

(8)

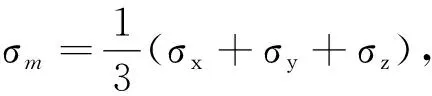
土壤模型的建立需要3个参数：粘聚力C、内摩擦角φ及膨胀角φ.膨胀角用来控制体积膨胀的大小，对于压实的颗粒状材料，当材料受剪时，颗粒就会膨胀。

对于DP模型，如果已知单轴受拉屈服应力和单轴受压屈服应力，则内摩擦角和粘聚力可表示为

(9)

(10)

式中β和σy与受压屈服应力和受拉屈服应力的关系为

(11)

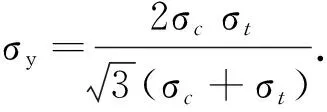
(12)

利用有限元软件对土块进行离散处理，选择DP模型后，对其密度、弹性模量、密度、内摩擦角及粘聚力等土壤参数进行定义，如表1所示。

表1 不同硬度的土壤参数

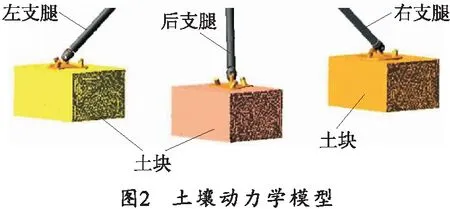
对土块进行单元设置及网格划分，并在其与外界连接处建立界面点，使用模态综合法计算得到描述土壤形变的模态集，通过软件接口程序生成ADAMS可识别的中性文件，最终在柔性土壤的界面点施加约束和载荷，完成刚柔耦合模型的建立。笔者所建立刚性支腿与柔性土壤的刚柔耦合模型如图2所示。

1.4 发射载荷加载

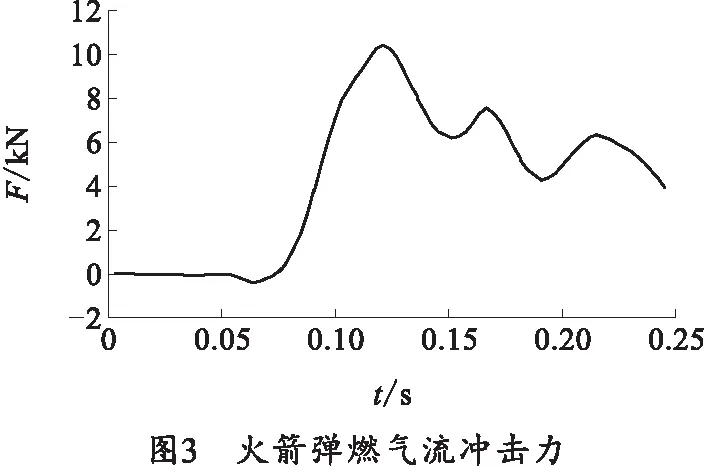
火箭炮的发射过程是一个复杂的随机过程，受到众多随机因素的影响，如温度、压力及每发火箭弹冲击力，但火箭弹燃气射流是火箭炮发射装置主要载荷[14]。笔者设置合理边界条件后应用CFD软件得到火箭弹燃气流对火箭炮架体的冲击力，如图3所示。

1.4.1 作用在火箭弹上的推力

火箭弹发动机的推力使火箭弹产生加速度，同时也引起弹-箱系统的相互作用。根据厂家提供的参数，该火箭弹发动机推力约为12.1 kN，工作时间1.3 s，达到稳定推力时间为0.006 s，将其加载于火箭弹的尾部。推力函数采用拟合函数AKISPL：AKISPL(time，0，Spline_1,0)，time为仿真的当前时间；Spline_1为推力曲线，以推力数据点的形式写入ADAMS中。

1.4.2 火箭发动机燃气射流对发射装置的冲击力

火箭弹燃气流冲击力直接作用与发射箱表面，其数值大，作用时间短，且在火箭弹出管后低头，因火箭弹与定向管的轴线形成夹角，燃气流不仅在定向管轴线方向施加作用力，而且会在定向管下方，垂直于定向管轴线向上施加作用力，分析此时燃气流在垂直轴线的冲击力，取值为燃气流轴线方向冲击力的sin 0.3°[10].

对于建立模型的可信度，主要考虑所建立模型的刚度、阻尼与实际土壤特性相符合。笔者采用支腿受力及火箭炮定向器炮口振动特性验证其可信度。首先采用支腿受力作为计算和试验的对象，将模型放置于土壤硬实地面，支腿作固定措施，方向角0°，高低角80°，发射箱中间发射位发射1发火箭弹，在右、后支腿安装拉压力传感器，如图4所示，振动加速度传感器安装于定向管口。

提取试验数据与仿真数据做对比分析，结果如图5～7所示。仿真数据与试验数据误差控制在10%以内，且运动趋势相同，所建立的土壤模型具有可信度。

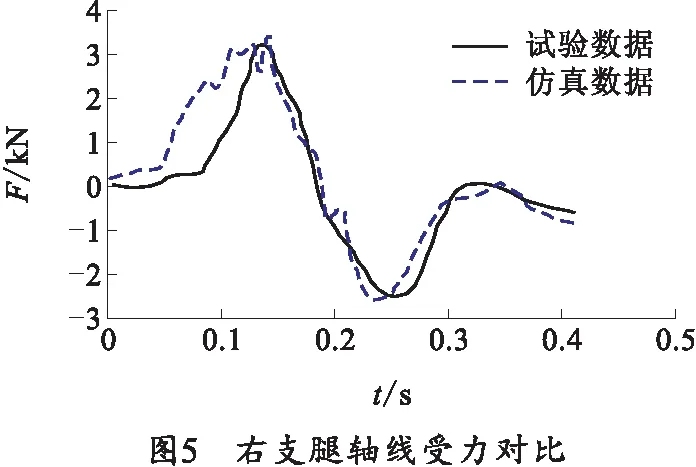
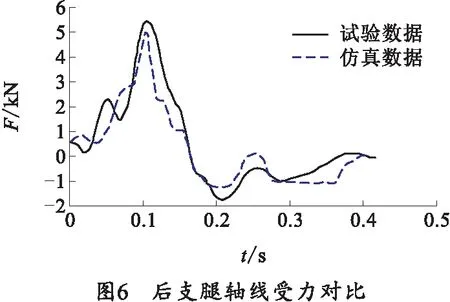
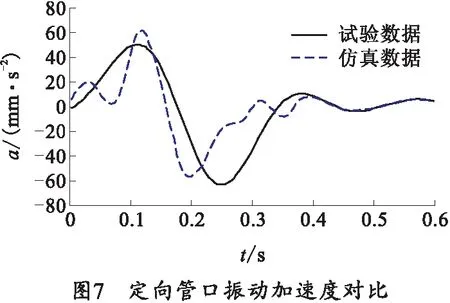
对比右支腿及后支腿受力数据，分析得到如表2～4所示的结果。

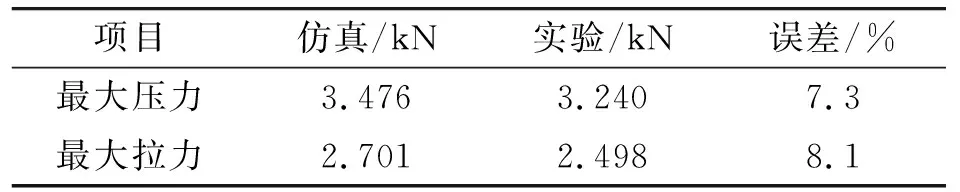
表2 右支腿所受最大拉压力及仿真误差

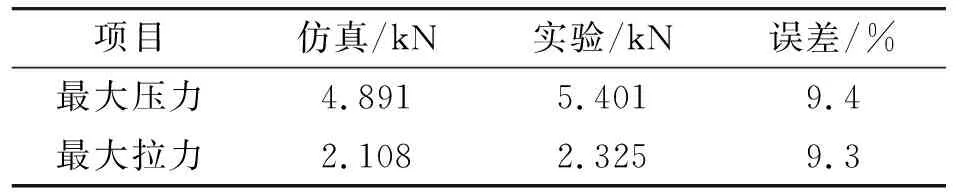
表3 后支腿所受最大拉压力及仿真误差

表4 定向管口垂直振动加速度

2 土壤硬度对火箭炮初始扰动影响计算

火箭弹从定向器上滑离的瞬间，弹体的纵轴及质心的速度矢量不沿定向器轴线所确定的理论射向，此时弹所具有的角速度为初始扰动，其主要包括方向和高低两个方面。火箭弹在铅垂面内的初始扰动为[15]

(13)

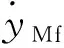
式(13)为对于单发射击的情况下计算结果，对于多联装武器，可通过式(14)来评价火箭炮整体初始扰动(中间偏差)的大小：

(14)

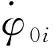
为保证土壤硬度为唯一变量，3种计算情况采用同一计算模型，仅改变影响土壤硬度的弹性模量、密度、内摩擦角及粘聚力，首发弹计算结果如图8～10所示。

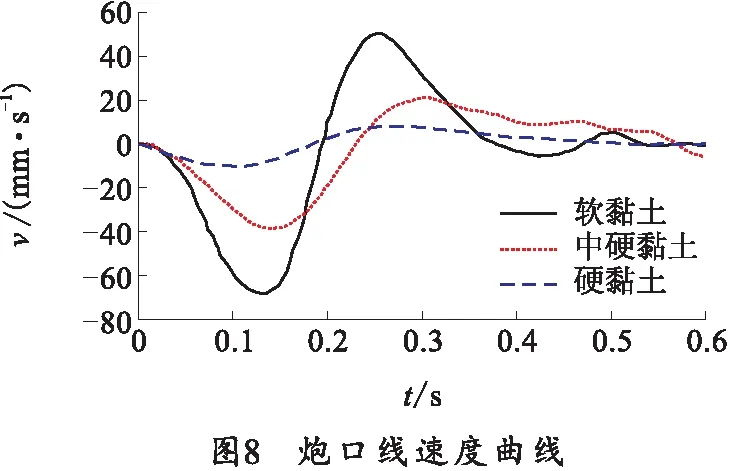
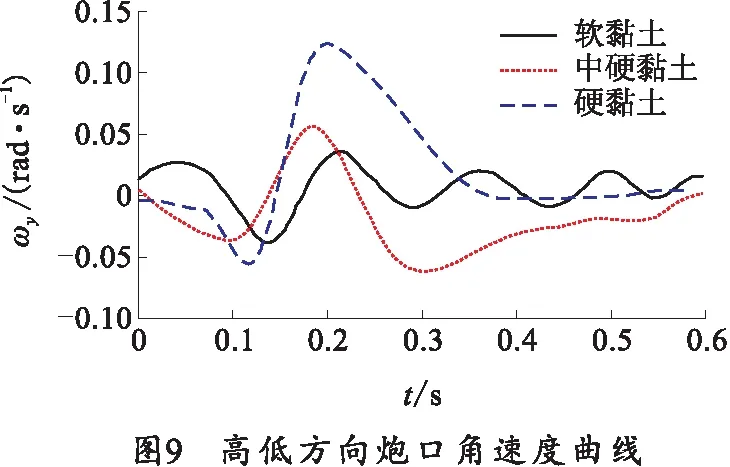
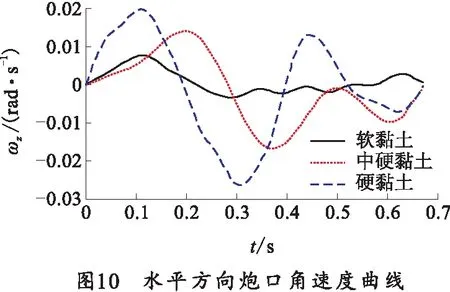
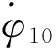
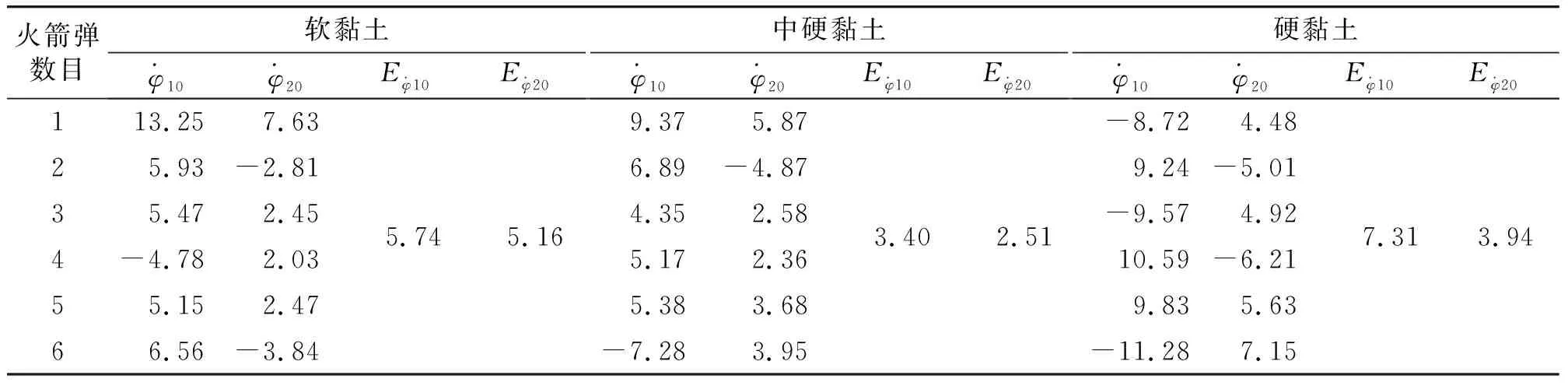
表5 不同土壤硬度条件下的初始扰动与中间偏差 mrad/s

从计算结果及分析可以得出，中硬度的黏土为土基发射时的初始扰动最小；土基为软黏土时，火箭炮发射时首发火箭弹初始扰动最大，原因为土质松软，受冲击载荷后土壤变形大，之后数发火箭弹发射时，土基压实，初始扰动变小；中硬黏土具有同样特性，但首发初始扰动较软黏土小；硬黏土为土基发射时，土壤形变很小，所吸收能量少，其振动由发射架体吸收，整体跳动较大，使初始扰动及中间偏差变大。