新型扭簧式平衡机设计

马浩，高跃飞，周军，王钊

(中北大学 机电工程学院，山西 太原 030051)

遥控武器站是一种安装在多种平台上相对独立的模块化、通用化武器系统，其最大特点就是车辆乘员不必暴露在车外就可以直接操控武器精确射击[1]，其上可以配置多种武器和不同组合的火力控制系统[2]。当遥控武器站上配备了小口径武器以后，俯仰机构的质心不在耳轴轴线上，而是相对耳轴前移，故在武器的俯仰过程中，会产生动态变化的不平衡力矩，对武器射击的稳定性产生负面影响[3]。武器俯仰过程的不平衡力矩可以采用平衡机来补偿，需要设计适用于武器站的结构紧凑、质量轻的平衡机。

平衡机在大中口径武器上已有广泛的应用，结构形式和种类较多，常见的有弹簧式和气压式两种。弹簧式平衡机因其结构简单、工作可靠且受外界环境因素影响低等优点在小口径武器上得到了较多应用。张海洋等[4]设计了一种通过弹簧与链轮链条配合来实现平衡重力矩的平衡机；陈雷等[5]针对小口径武器采用发条簧和滑轮配合的方式设计了一种带蜗轮蜗杆机构的发条簧式平衡机；康郦等[6]设计了一种安装在舰炮耳轴上后方的发条簧平衡机，并对该平衡机的动态和静态情况进行分析和调试。纵观上述弹簧式平衡机的应用，不难发现其结构组成具有相同的特点，即在原有武器结构的基础上增添了定滑轮和链轮等机构，使得武器的结构设计复杂化，除此之外，上述部分平衡机的设计使用了蜗轮蜗杆机构，增加了平衡机结构设计的复杂程度。为了简化武器结构设计，使平衡机结构更加紧凑、简单，笔者提出了一种新的平衡机设计思路，使用扭转弹簧将平衡机与耳轴部分结合起来，即平衡机与耳轴同轴。这种结构既减少了上述平衡机所需的滑轮绳索机构，又降低了平衡机自身结构的复杂程度。

1 平衡机结构

某遥控武器站实物如图1所示。遥控武器站主要包括火力分系统、火控分系统、供配电分系统和配套件连接件[5]。火力分系统则包括武器、摇架、上架和供弹机构等。平衡机位于摇架与上架相连的耳轴上。

图2为机枪遥控武器站火力分系统结构图。遥控武器站的机枪安装在俯仰机构的摇架上，摇架通过耳轴结构与上架连接。电动机、锥齿轮组和蜗轮蜗杆机构组成遥控武器站的高低机，安装在遥控武器站的边侧，平衡机则安装在与耳轴同轴位置的另一侧。

在平衡机内，扭转弹簧套在耳轴上，一端与上架处弹簧挡杆配合，另一端与耳轴处弹簧挡杆配合，弹簧挡杆通过螺纹固定在上架和耳轴的对应位置，如图3所示。

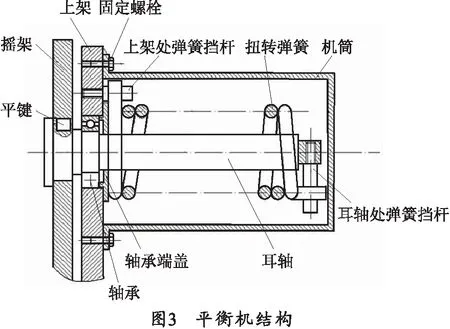
平衡机的工作过程如下：电动机通过锥齿轮和蜗轮蜗杆结构带动摇架进行俯仰动作，摇架相对于上架绕耳轴轴线进行转动。由于上架不动，耳轴转动，迫使扭转弹簧两端产生角度差，使得扭转弹簧变形产生一个扭力，为俯仰部分提供一个力矩来实现其平衡机的作用。到达指定射角后，电动机停止转动，机枪和摇架通过蜗轮蜗杆机构的自锁性能固定在指定射角。

2 模型的建立及计算

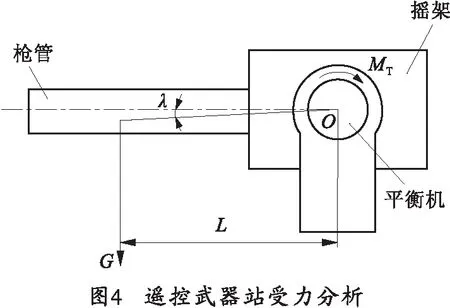
为便于对平衡机特性的分析及设计，建立遥控武器站的简化模型，如图4所示。图中，G为俯仰部分重力，MT为平衡机提供的力矩，L为质心与耳轴回转中心之间的距离，λ为初始时刻(射角为0°时)质心与耳轴支点两点之间的直线与水平面之间的夹角(顺时针为正)。

该遥控武器站的基本参数如表1所示，表中φ为遥控武器站的射界，ω为遥控武器站俯仰过程中耳轴所能达到的最大转速。

表1 遥控武器站部分参数

2.1 重力矩计算

当遥控武器站俯仰一定射角θ时，其所产生的重力矩为

MG=GLcos(θ+λ).

(1)

遥控武器站实际工作过程中，射角是变化的，重力矩随射角的变化关系如图5所示。

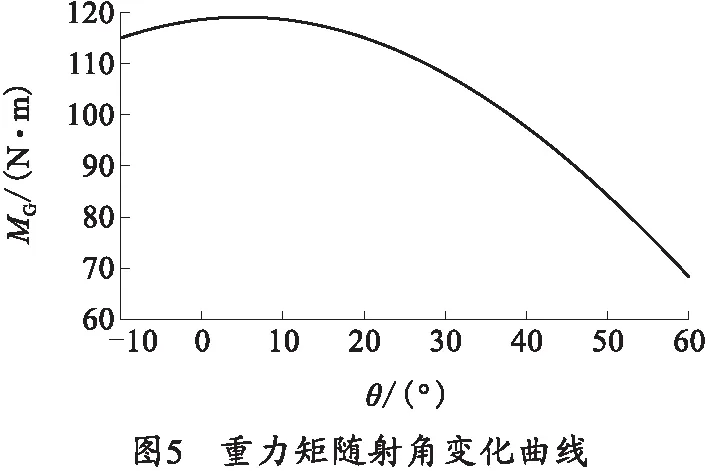
由图5可知，随着射角的增加，重力矩先小幅度增大然后逐步减小。因此，平衡机所提供的力矩也应随射角的改变按上述趋势变化。

2.2 平衡机力矩计算

平衡机的作用是为了减小在不同射角时重力矩带来的影响，因此平衡机提供的力矩曲线应与在各射角位置时的重力矩接近，以减小二者的差值，即不平衡力矩尽量小。

由于平衡机设计在耳轴上，因此弹簧具有的扭转力矩就是平衡机提供给武器俯仰部分的平衡机力矩。在扭转弹簧的线性工作区内，扭转弹簧提供力矩随射角的变化关系为

MT=Kθ，

(2)

式中K为弹簧的扭转刚度。

平衡机的设计方法有两种：完全平衡法、两点平衡法或三点平衡法[7]。完全平衡法需要有特定的结构布置或采用配重来实现，实用性差，因此笔者选用两点平衡法来对该扭簧式平衡机进行设计。在整个射角范围内，调整平衡机的结构参数，对弹簧刚度K进行优化，得到射角0°和57°两个平衡点，即在射角0°和57°时平衡机力矩和重力矩大小相等，方向相反。根据扭转弹簧的工作特性曲线可得弹簧刚度的计算公式为

(3)

式中:θ1和θ2分别为两平衡点处射角0°和57°；MG1和MG2分别为射角θ1和θ2处的重力矩。

确定平衡机的弹簧刚度K后，即可由平衡机的工作原理计算出俯仰过程中的平衡力矩的变化规律。平衡机力矩的变化曲线如图6所示。

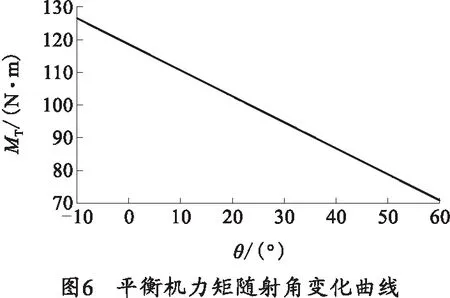
由图6可知，随着射角的增大，平衡机力矩在不断地减少，大致符合重力矩的变化趋势。

2.3 不平衡力矩计算

不平衡力矩是由于重力矩和平衡机力矩在对应的角度下不能做到完全平衡而存在的力矩。根据不平衡力矩的定义可以得到不平衡力矩计算公式：

ΔM=MG-MT.

(4)

将式(2)和(3)代入式(4)，可求出在该平衡机作用下的不平衡力矩变化规律，如图7所示。

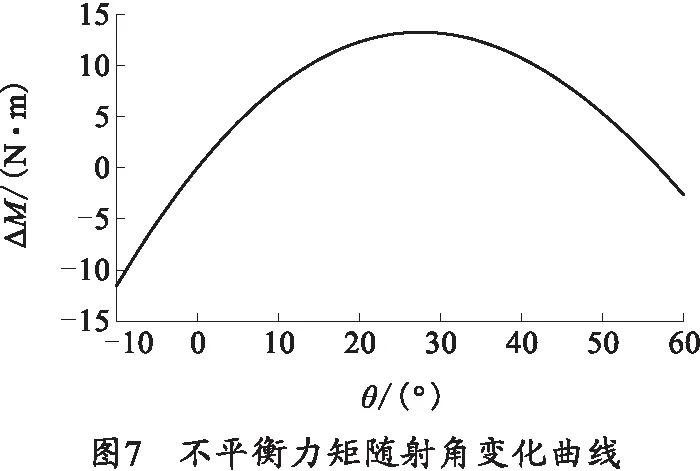
由图7可知在整个过程中，不平衡力矩最大值不超过15 Nm，远小于无平衡机时的最大重力矩。由此可见，该平衡机能够有效地减少重力矩在俯仰过程中对武器操控的负面影响，起到了平衡重力矩的作用，达到了遥控武器站对平衡机的工作要求。

3 扭转弹簧设计

根据遥控武器站的工作条件和平衡机力矩的计算结果可知，在武器站的整个俯仰工作过程中，弹簧工作转动角度φ为70°，承受的最大扭矩Tmax为126.713 Nm，承受的最小扭矩Tmin为70.038 8 Nm，即扭转弹簧的预压扭矩为70.038 8 Nm. 该扭转弹簧材料选择60Si2MnA，抗拉极限强度σb为1 471 MPa，许用弯曲应力值σBp为1 232 MPa，弹性模量E为206 GPa.

根据扭转弹簧的设计计算方法[8]，弹簧的曲度系数为

(5)

式中C为弹簧旋绕比，为使结构紧凑初定旋绕比为6.

弹簧钢丝直径可确定为

(6)

则，中径D为

D=Cd.

(7)

弹簧的有效圈数为

(8)

设计弹簧的弹簧刚度为

(9)

其工作极限扭转力矩为

(10)

式中，σj为工作极限弯曲应力，σj=0.8σb.

则弹簧的工作极限扭转角为

(11)

弹簧节距为

t=d+δ，

(12)

式中δ为弹簧间距，若无特殊要求取0.5 mm.

弹簧自由长度为

H0=nt+d.

(13)

弹簧螺旋角为

(14)

根据设计要求，通过数值计算，得到扭转弹簧参数最优解如表2所示。

表2 扭转弹簧参数

4 动力学分析

当武器站俯仰机构转动到指定射角电动机停止转动时，平衡机、俯仰机构和高低机三者构成的弹簧-阻尼系统在惯性的作用下会发生振动，不利于火炮对目标的跟踪。笔者以最大射角为例，分析当武器站转动到指定射角时该弹簧阻尼系统的稳定性。

为了更好地了解扭簧式平衡机的工作特性，可利用虚拟样机技术对该遥控武器站在其射界内的俯仰运动进行动力学仿真分析，从而得到武器站在工作过程中的重力矩、平衡机力矩以及不平衡力矩的变化情况，以及武器站俯仰部分运动停止时的武器系统的稳定性情况。

4.1 动力学建模

利用虚拟样机技术及软件可建立武器站及平衡机的虚拟样机模型，便于进行武器站运动的分析。

在三维软件NX中建立该平衡机的三维实体模型并将其以Paraslolid(.*x_t)格式导出，再通过CAD接口模块ADAMS/Exchange将其导入动力学分析软件ADAMS中进行动力学分析。ADAMS软件会自动根据带Lagrange乘子的第一类Lagrange方程建立多体系统动力学方程[9]。根据该遥控武器站工作过程中运动构件的运动规律，在不影响模型合理性的前提下进行如下假设：

1)武器站和平衡机的相关构件均按作刚体处理；

2)武器站俯仰结构和上架的各部件分别做一体化处理；

3)将扭簧式平衡机简化为扭转弹簧阻尼器，其工作参数与扭簧式平衡机参数相同。

按照武器站和平衡机在实际运动中相应的受力情况，分别对各零件添加约束和力元关系：

1)根据武器系统的实际结构情况调整俯仰部分的质心位置并赋予其实际质量；

2)上架与大地之间添加固定副，使它们相互固连；

3)根据俯仰过程中耳轴、锥齿轮、蜗轮蜗杆与上架之间的转动关系，分别在耳轴、锥齿轮、蜗轮蜗杆与上架之间添加转动副；

4)为了使锥齿轮和蜗轮蜗杆的传动更接近实际情况，笔者不采用ADAMS中自带齿轮副，采用impact力的碰撞模型分别在锥齿轮之间和蜗轮蜗杆之间建立力的接触将二者之间的传动关联起来；

5)在摇架和上架之间，在耳轴的回转中心处添加扭转弹簧阻尼器并输入上文中设计出扭转弹簧的相关参数，用以模拟俯仰过程中平衡机提供的力矩。

为模拟武器站在射界内的俯仰过程，在电动机处的转动副上添加转动驱动函数模拟电动机的驱动，带动锥齿轮和蜗轮蜗杆机构转动，驱动遥控武器站从最低射角-10°向最高射角60°转动。

虚拟样机模型建立完成，使用求解模块ADAMS/Solver进行仿真。

4.2 仿真结果与分析

仿真完成后对结果进行处理。得到的结果如图8所示。图8为不平衡力矩随射角变化的曲线，横坐标为遥控武器站的射角。

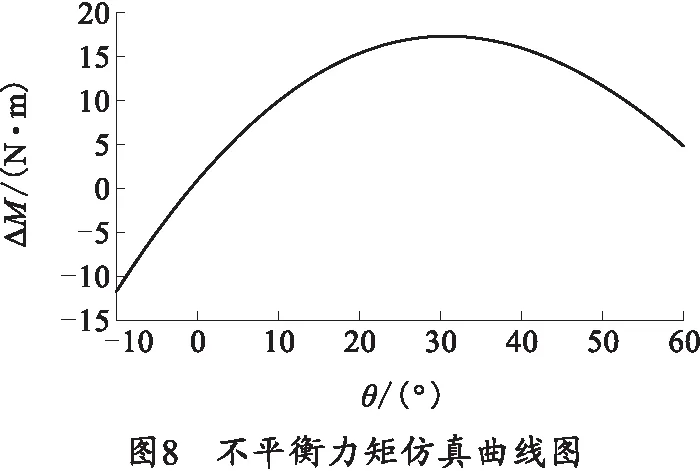
从图8可以看出，随着射角的增大，不平衡力矩从-10 Nm开始增加，在射角为31°时到达最大值17.5 Nm；之后开始减小，最终减小至5 Nm.在整个变化过程中，不平衡力矩绝对值的最大值为17.5 Nm，远小于该遥控武器站无平衡机时的不平衡力矩的最大重力矩120 Nm，满足平衡机的设计要求。

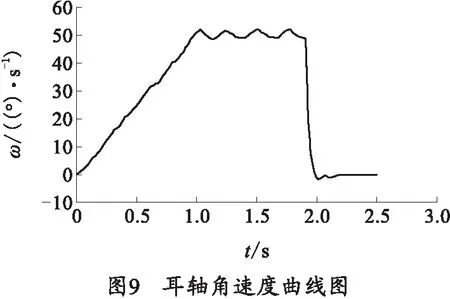
图9为耳轴转动角速度曲线。由图9可知，在1.9 s时刻，遥控武器站的俯仰机构运动到位，电动机停止工作，耳轴转速短时间内急剧减小，并在2 s附近出现波动，在2.2 s时，耳轴转速为0，即在耳轴达到最大转速时，遥控武器站能够在0.3 s内将其俯仰机构稳定下来，证明了该扭簧式平衡机既能起到平衡重力矩的作用，又能在到达指定射角时使遥控武器站具有良好的稳定性。

5 结束语

当前，武器轻型化是武器的一个重要研究方向。根据某遥控武器站的结构和工作要求，结合扭簧提供扭转力矩的原理，设计了一种新型与耳轴结合的扭簧式平衡机。该平衡机具有以下特点：

1)该扭簧式平衡机相比其他平衡机，在结构上更加简单紧凑。

2)该扭簧式平衡机的结构与耳轴部分相结合，直接为武器站的俯仰机构提供扭转力矩以降低重力矩俯仰过程中的负面影响，优化了武器的结构布置，有利于武器站朝着小型化、轻型化的方向发展。

3)通过数值计算和仿真分析可知，该扭簧式平衡机将不平衡力矩从120 Nm(无平衡机时的最大重力矩)降低到了17.5 Nm，极大地减少了重力矩在俯仰过程中对武器站俯仰机构的负面影响。除此之外，当武器转动到指定射角时，可在0.3 s内将由平衡机、高低机和俯仰机构组成的弹簧-阻尼振动系统稳定下来，具有良好的稳定性。