基于性能退化的身管多状态可靠性分析

康总宽，闫 彬

（西北机电工程研究所，陕西 咸阳 712099）

0 引言

身管是身管类武器的核心部分，是实现武器战术技术性能的关键零件，保证身管处于可用的工作状态，是保证身管类武器完成作战任务的关键环节。随着技术的发展，身管寿命得以不断提升，但日益频繁的使用及对服役状态要求的提高，使得有效评估身管在寿命周期内的可靠性显得尤为重要。充分利用使用过程中产生的与身管寿命有关的数据和信息，建立合适的方法可对身管寿命可靠性进行有效地分析与评估成为亟待解决的问题之一。

目前，身管可靠性评估主要集中于对身管疲劳寿命的评估和烧蚀磨损寿命预测，如采用理论计算的方法分析身管结构疲劳可靠性［1-2］、采用有限元方法进行身管可靠性分析［3］、基于多性能参数的身管寿命可靠性评估［4］、采用改进响应面法对身管可靠性进行设计与优化［5］等。这些方法偏重于从身管失效机理层面对其可靠性进行理论解释，基于身管“正常工作”和“完全失效”两种状态的“二元状态”可靠性理论，建立相应的算法和模型。上述可靠性分析方法无法体现出寿命周期内身管可靠性与性能退化的关系，不能很好地满足实际使用需求。

多状态理论能够更为真实地反映复杂系统工作历程。近年来，基于多状态系统理论的可靠性研究工作发展迅速，在电力、能源、航天、信息等工程领域得以成功应用，已成为复杂系可靠性研究的有力工具和关键技术手段［6-9］。实际使用过程中，身管寿命终止并不是一蹴而就的，而是经历多种功能性能退化［10］状态，一定时期后才完全失效。因此，从多状态理论角度来看，身管可视为一个多状态不可修复零件。基于监测数据，采用K 近邻聚类［11-12］方法划分身管性能状态，继而采用多状态理论进行身管可靠性评估，建立基于性能退化的身管多状态可靠性评估方法，可进一步充实完善身管可靠性研究理论与方法。

综上所述，本文以身管为研究对象，利用K 近邻聚类方法对试验数据进行聚类分析，划分了寿命周期内身管所经历的状态迁移过程，采用连续时间马尔科夫链模型，建立了身管寿命多状态可靠性分析模型，在此基础上对某身管寿命可靠性参数进行了计算和评估，为发展身管武器多状态可靠性分析方法提供了借鉴。

1 身管多状态可靠性

1.1 身管寿命及性能状态参数

在身管服役期间，受到发射时火药燃气烧蚀、弹丸机械磨损、交变热应力、化学腐蚀等作用，以及不同工况的影响，身管损伤不断累积，性能逐渐退化，直至寿命终止。换言之，身管在服役期间性能从完好状态逐渐跃迁至寿命终止状态，不存在性能提升。

身管的失效主要表现形式为身管寿命终止。通常情况下，身管的疲劳寿命远大于其烧蚀磨损寿命，身管在弹道寿命终结之前，不会发生疲劳失效现象。现有的身管寿命终结判据之间存在很强的耦合性，各判据出现的原因都可归结为身管内膛的烧蚀磨损，因此，进行身管寿命可靠性分析时，内膛的磨损量可作为身管多状态可靠性评估的性能状态参数。

反映身管状态的内膛磨损分布于身管整个导向部，这些参数彼此间具有较强的耦合关系，根据身管的寿命试验和实际使用经验，身管导向部距坡膛结束点一定距离处的磨损最为剧烈，该处磨损量的变化有着较为特殊的规律，使身管表现出多态性特征。

1.2 基本假设

身管寿命多状态可靠性分析方法有以下假设：

1）身管为不可修复零件。

2）身管寿命终止的判据为身管弹道性能降低到战术技术指标规定的允许值以下。

3）进行寿命周期内身管多状态可靠性分析时，只考虑烧蚀磨损产生的退化失效，即身管的疲劳寿命大于弹道寿命。

4）身管导向部不同点的磨损量具有相关性，根据身管寿命判据，以烧蚀磨损最恶劣点为性能状态参数。

1.3 多状态可靠性

对身管来说，其状态迁移只能从状态gm向状态gn迁移（m＞n），当身管的性能状态迁移至不可接受状态，则寿命终止。

在身管的寿命周期内，除非出现意外情况，身管的失效过程是一个渐变过程。随着射击发数的增加，首先，在射击一定发数后性能出现下降，进而一段时间之后功能逐渐恶化，最后，随着射击发数达到规定发数，弹道功能和性能完全丧失。

身管在服役期间，需完成一定的射击任务，即需要满足任务对输出性能参数的要求。身管寿命多状态可靠性可定义如下：身管在规定条件下，规定时间内，在t 时刻对应的状态满足任务要求的程度，即身管的烧蚀磨损剩余量满足任务要求的概率。

身管在寿命周期内多状态可靠性可采用可用度、可靠度、期望性能输出和期望性能失效4 个指标进行度量［7］。

2 身管多状态可靠性分析

2.1 多状态可靠性评估方法

工程实践表明，二元状态应用于系统可靠性评估时，不能刻画系统由于性能退化引起的多态性特征，而多状态系统可靠性分析与评估方法，能够较为准确地刻画系统的真实运行状态。多状态是指系统的实际性能不局限于二元状态，而是存在多种不同的状态［13-14］。

多状态系统可靠性分析方法注重系统可靠性与部件性能之间的关系，具体到身管可靠性分析，可由身管的性能退化状态建立相应的可靠性分析模型，求解寿命周期内多状态条件下的身管可靠性。

多状态系统的状态数量一般按照其功能状态确定，但是，很多系统并不具有显而易见的功能状态，利用数据驱动的方法，对试验记录数据或状态监测数据进行聚类分析，是获得多状态系统状态模式和数量的有效方法。

多状态系统可靠性分析与评估方法主要包括4类［15］：布尔扩展模型法、马尔可夫模型法、通用生成函数法和蒙特卡洛仿真法。其中，马尔可夫模型法能够描述系统各状态间的时变规律与失效机理，可用于多状态单调系统稳态特性和可靠性的分析与评估。

2.2 K 近邻聚类状态划分方法

K 近邻是一种基于划分的机器学习方法，算法简单实用，广泛应用于故障诊断、状态监测等多个领域的分类问题。作为一种数据驱动的聚类方法，K近邻聚类算法通过聚类中心迭代重定位技术，实现数据的快速聚类，其评价指标基于距离相似度，把距离较近的数据作为最终聚类目标，两个聚类对象间的距离越靠近，它们就越相似［16-17］。

本文采用欧氏距离作为K 近邻算法的相似性度量，假设样本各维度特征向量权值相同，算法实现流程如下：

2.3 连续时间马尔科夫链

连续马尔可夫链任意时间历程所处状态j 的概率取值，完全取决于其初始时刻所处状态i 的概率取值，以及时间间隔t 内i、j 两类状态的迁移函数ξij的概率取值［6］。

假设连续时间马尔可夫链在完成状态i 向状态j 迁移过程中，不是一步完成，而是先迁移至中间某一状态k，而后再迁移至状态j，则可得连续时间马尔可夫链的Chapman-Kolmogorov 方程：

2.4 连续马尔可夫链通用解算微分方程

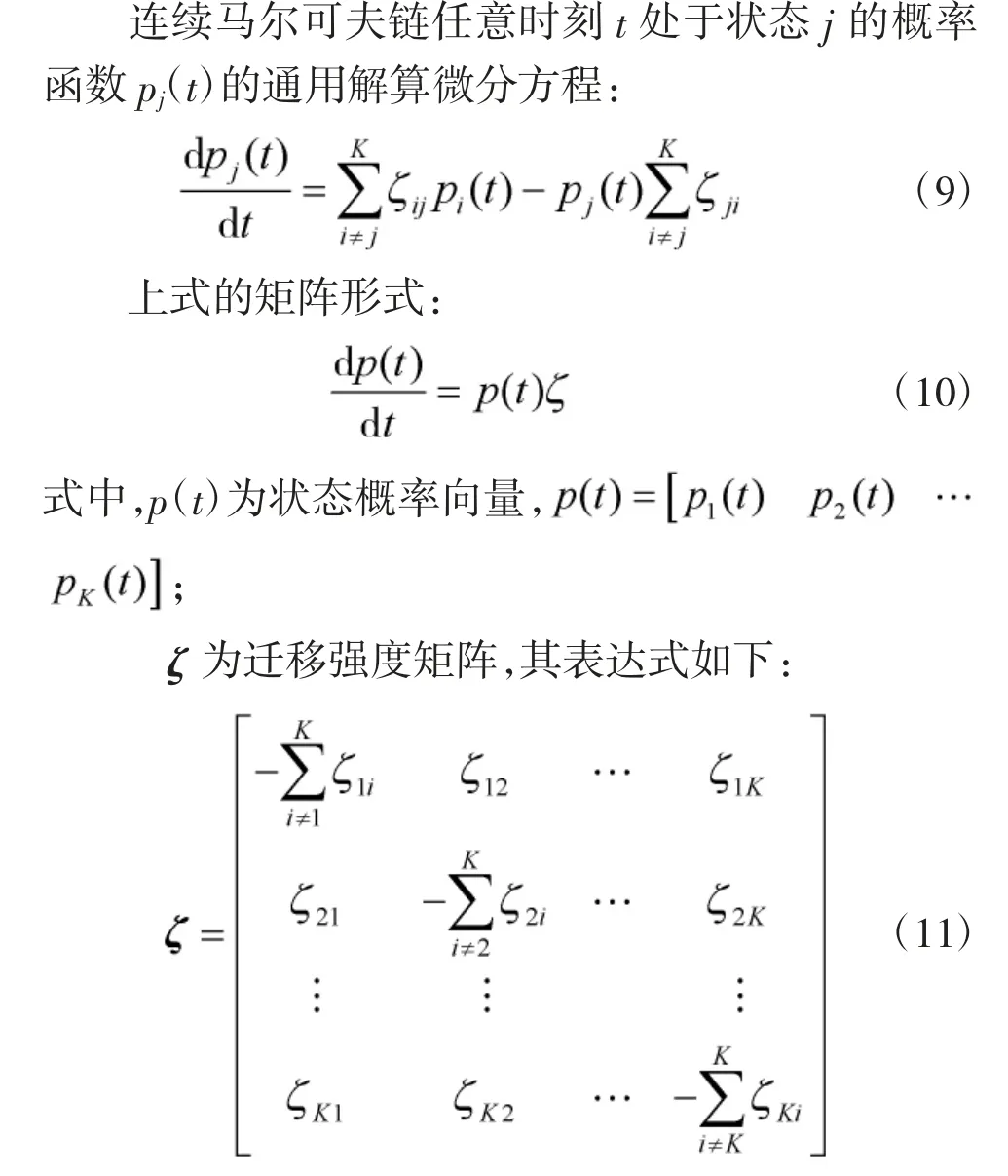
2.5 身管多状态可靠性评估模型

在实际服役和使用过程中，身管属于不可修复零件，根据多状态可靠性理论，身管在寿命周期内的失效模式仅存在由gk状态向gk-1状态迁移一种可能，如图1 所示。

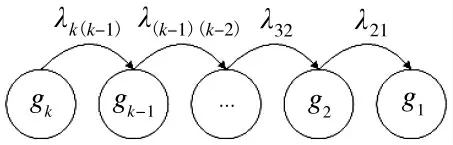
图1 身管失效模式

根据式（11），身管的状态概率通用解算微分方程形式如下：

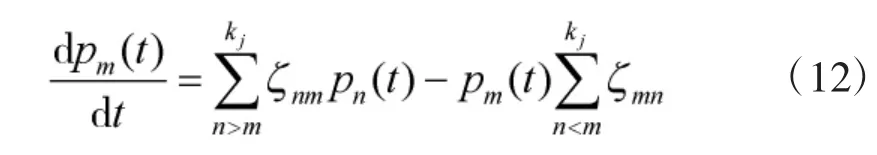
从式（12）可以看出，不可修复零件状态迁移过程始终具有功能失效趋向，即始终从gk状态向gk-i状态迁移；不存在功能恢复或提升的可能，即不存在gk-i状态向gk状态或gk+i状态迁移的可能。

3 算例分析

某身管试验过程中对内膛磨损量进行了监测，试验过程中设置了多个测点，每射击10 发测量身管内膛各测点磨损量一次，并计算各点磨损率［18-20］。本文选取距炮口距离不同的5 个测点数据进行基于性能退化的多状态可靠性分析，选取测点处的磨损量和磨损率变化如图2 所示。通过分析试验测试数据，并进行合理推算，证实身管内膛距炮口5 150 mm处烧蚀磨损最为恶劣，如图2 所示。内膛距炮口5 150 mm 处烧蚀磨损量达到4.979 mm，该点的磨损量及磨损率监测数据如下页表1 所示。基于上述，从身管性能的退化出发，采用多状态可靠性分析方法，利用试验监测数据对该身管的可靠性进行分析，并计算反映可靠性的各个参数。

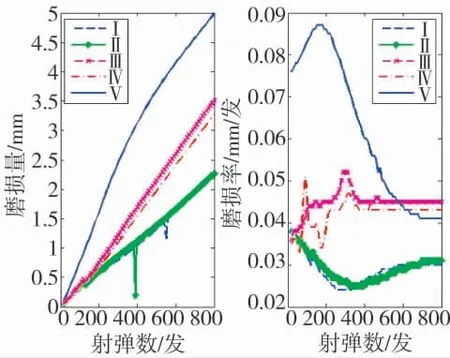
图2 身管内膛各测点的磨损量和磨损率

身管射击时，内弹道时间只有十几毫秒至几十毫秒，其寿命按照时间历程进行计算很短暂，根据身管类武器的工程特点，采用射击发数作为时间轴，表征身管的寿命。在身管的服役过程中，每次射击完成后都会进行相应的维护保养，因此，从身管全寿命周期来看，不用时间段的射击可视为连续使用状态。下面的可靠性分析过程按照连续变化过程进行处理。

3.1 身管多状态聚类分析

选取试验身管内膛距炮口5 150 mm 测点作为身管性能退化参考点，该点的磨损率和剩余磨损量变化如图3 所示。身管在寿命周期内每次射击都可视为一种独立状态，根据实际工况及试验数据分析，将具有相似特点独立状态划分为一大类，从而在较长时间尺度上建立身管的多种状态。

K 近邻聚类比较容易实现上述状态划分，采用磨损率作为基本数据，进行身管性能退化状态聚类分析。选取聚类数量初值K=5，并随机选取5 组磨损率数据作为聚类中心，进行身管功能状态聚类分析。根据选取的性能状态数据，上述过程为一维数据的K 近邻聚类过程，聚类的结果是将身管的可用性能状态分为3 个类别：状态g4，状态g3和状态g2，聚类分析结果如图4 所示。

表1 某身管试验过程中内膛磨损量和磨损率

根据聚类分析结果，以及身管在射击过程中单发磨损率的变化，将身管在寿命周期内的状态分为4 类，即功能下降状态g4，持续时间约310 发，这一状态磨损率最大；功能恶化状态g3，持续时间约170发，磨损率逐渐下降；功能稳定状态g2，持续时间约320发，磨损率趋于稳定；功能失效状态g1，磨损量达到弹道磨损极限。各状态划分及划分依据、持续时间如表2 所示。

图3 参考点磨损率和剩余磨损量曲线

3.2 身管多状态可靠性评估模型

根据连续时间马尔科夫链建立的多状态可靠性评估方法，求解寿命周期内身管可靠性，其通用解算微分方程为：

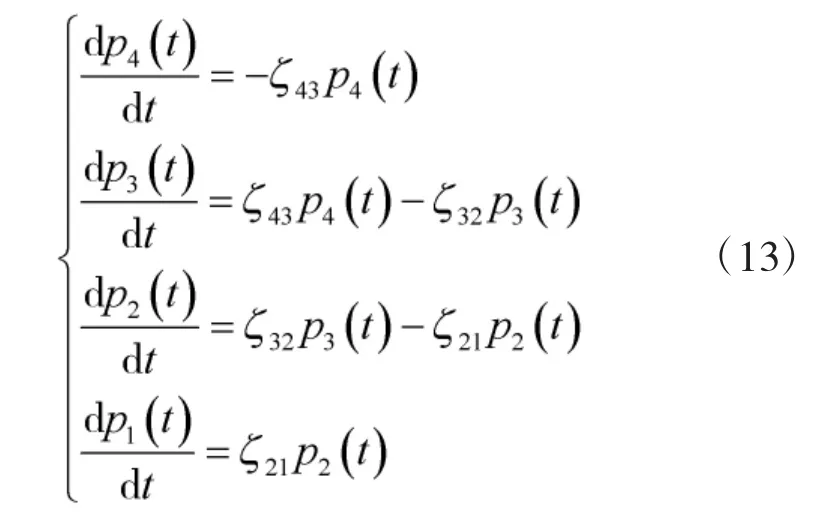
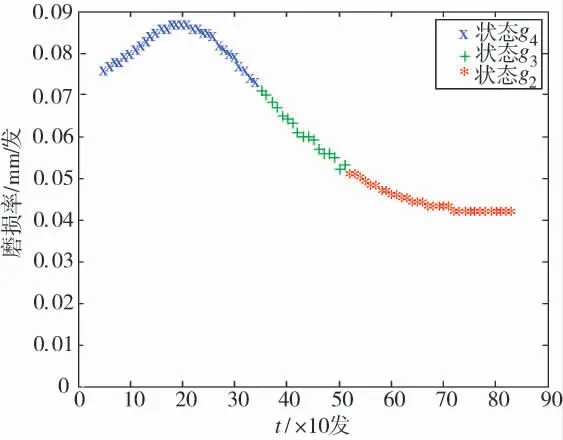
图4 身管性能状态K 近邻聚类结果

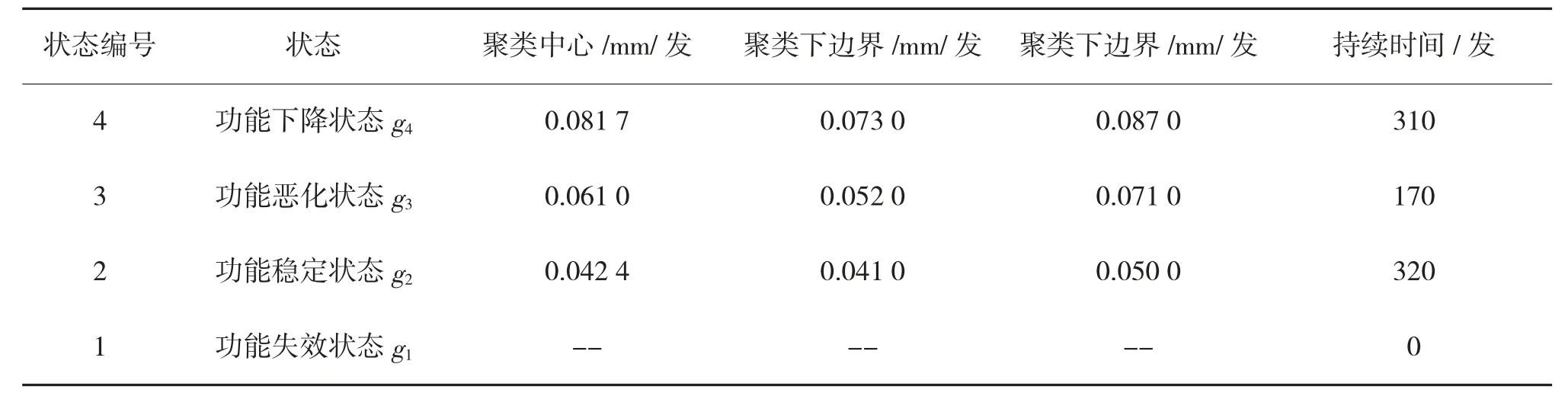
表2 身管状态划分及划分依据列表

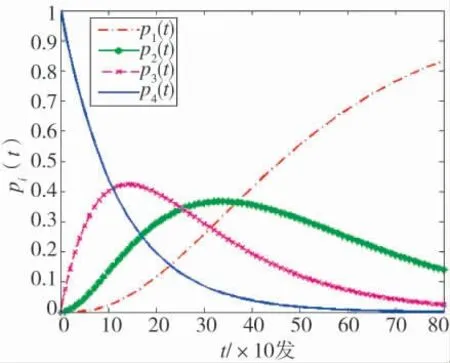
图5 寿命周期内身管状态变化规律

3.3 身管可用度和可靠度分析

基于上述分析，采用多状态可靠性理论计算身管可用度，为身管的实际服役及满足任务需求程度提供定量评估。

身管可用度指标A（t）是指身管在时刻t 处于可用状态的概率。由于身管的不可修复性，其可用状态仅包括功能和性能降级状态，即A（t）的值是身管在时刻t 处于功能初始下降、功能恶化状态、功能稳定状态的概率之和，可用度A（t）可由下式计算：

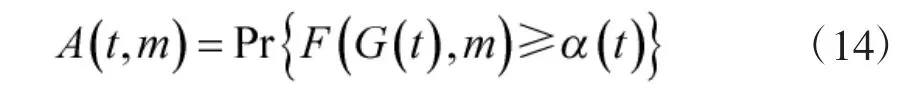
当身管处于正常使用工况时，门域函数α（t）取恒值0，身管功能输出函数G（t）取某一任务期内身管所处的状态gi，当该任务期内最低射弹数为m时，可接受度函数F（t）取值G（t）-m。

身管可用度的计算分析以满足不同任务需求为目的，假设该作战时弹药基数为100 发，任务需求为2 个弹药基数，即200 发射弹数，其可用度分析如下：

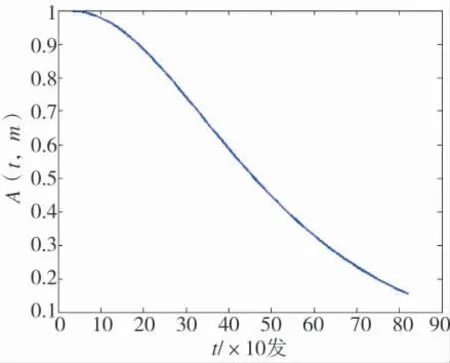
图6 身管可用度曲线

身管可靠度是指在寿命周期内，处于可接受功能状态的概率。从整个寿命周期来看，虽然身管经历了几个不同的性能状态，且性能逐渐退化，但是，直到性能下降到g1状态之前，身管都具备可用的弹道功能，处于可接受的功能状态。因此，身管可靠度可由式（15）进行计算：

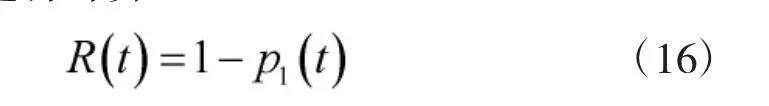
根据上节计算结果，当身管任务需求为200 发射弹数时，其可靠度等于可用度。

3.4 身管期望性能输出和期望性能失效

身管的输出性能，以及输出性能满足任务需求的能力，是工程中较为关注的问题，也是可靠性的重要评估参数。稳态情况下的期望性能输出表征身管的输出性能；稳态情况下的期望性能失效表征身管期望性能输出与期望性能需求之间的偏差，反应性能输出不能满足期望需求的水平。

假设遂行射击任务时对身管的期望性能需求分别为200 发射弹数，根据上面的分析结果，进行期望性能输出和期望性能失效分析，则期望性能输出：

期望性能输出和期望性能失效计算结果如下页图7 所示。鉴于身管的不可修复性，稳态期望性能输出GE（∞）随着射弹数增加逐渐趋近于0，稳态期望性能失效GE（∞，200）随着射弹数增加逐渐趋近于200 发。根据计算结果，假设当前身管剩余寿命为已射击200 发，遂行射击任务期望性能需求为200 发时，身管的期望性能输出GE（∞）=255 发，期望性能失效GE（∞，200）=83 发，满足任务需求。但是，随着身管寿命的增加和一次任务射击发数的增加，期望输出快速下降，期望性能失效则显著增加，这意味着随着身管射击发数的增长，其执行任务的可靠性不断下降，与身管的实际使用工况相符合。

图7 身管期望性能输出和期望性能失效

通过对寿命周期内身管的多状态可靠性分析，以及对可靠性指标的计算，建立了身管性能退化与可靠性之间的关系，有助于检验身管的使用边界，以及制定更为合理的射击规范；同时，为身管作战效能的发挥提供了理论依据。

4 结论

本文针对身管寿命周期内可靠性分析问题，提出了基于K 近邻聚类和性能退化的多状态可靠性分析方法。通过工程案例，对处于正常寿命周期内的身管性能状态进行了K 近邻聚类，划分了身管性能状态，分析了身管多状态可靠性，计算了可靠性度量指标，证明了多状态可靠性评估方法的有效性，为今后研究身管类武器可靠性提供了新依据。本文仅对身管类武器的关键零件，在正常寿命周期内的可靠性进行了分析，然而，在工程中身管类武器是由多种零部件和子系统组成的较为复杂的系统，其可靠性评估都是系统层面的，如何根据身管类武器的特点进行系统层次的多状态可靠性评估，是今后亟待解决的问题。