探究直观想象在非几何问题中的运用
2021-05-12广州市南沙麒麟中学511455武志容
广州市南沙麒麟中学(511455) 武志容
新的课程标准指出高中数学教学由以前的三维目标: 知识与技能、过程与方法、情感态度与价值观上升到六大核心素养: 数学计算、数学抽象、直观想象、逻辑推理、数据分析、数学建模,从学生个人的技能提升到个体的全面发展,从具体的操作步骤到高度的概括提炼,是从量变到质变的一个飞跃,也从更高程度上要求我们在整个高中数学的学习过程中要高度的重视和不断的渗透这些核心素养,只有掌握好了它们才能真正的学好高中数学,才能在各种考试中立于不败之地.新教材新高考倡导的新题型很多时候也需要我们有很好的直观想象能力作为一个突破点.
直观想象可以说是这六大核心素养中最容易理解和接受的,但正如武术中的太极一样,看似简单却不易掌握,只有真正的武林高手才能做到游刃有余、以柔克刚、化腐朽为神奇.众所周知几何问题是直观想象的最好体现,除此之外直观想象在非几何问题中也有非常多的运用,我们结合近几年的高考题重点考察非几何问题.
一、有图有形,直观+想象
例1(2020年高考全国Ⅰ卷理科第5 题)某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位°C)的关系,在20 个不同的温度条件下进行种子发芽实验,由实验数据得到下面的散点图:
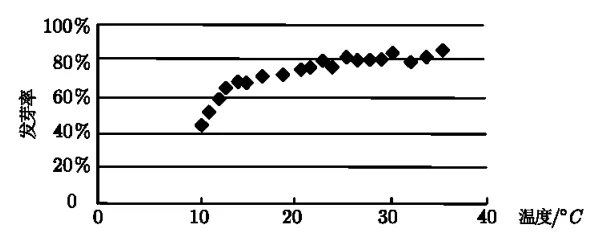
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A.=ax+bB.y=a+bx2C.y=a+bexD.y=a+blnx
解题分析这道图形题非常的直观,但不同层次的同学看到这道题的感觉是不一样的: 低层次的同学会马上错选A,因为就回归方程来讲线性回归方程相对比较熟悉,平时练习也较多;中层的同学可能关注点是在这20 个数据上,虽然给了坐标但没有给出具体的对应值,只能估算,但20 个数据估算起来也很困难,况且这里的a,b都未知,所以最后会陷于一种比较困惑的状态;稍好的同学会知道直接看图再加一点自己的想象,不需要计算,只需根据图形的大致形态,再结合各个函数图象的特点,直接找出与之吻合度较好的对数函数模型,直接看出答案D,既快又准.
像这种有实际应用背景的题目是近几年高考的热点题型,它把数学融入实际生活中,让我们了解数学在生活中的应用情况,并深刻体会到数学是一门非常有用的学科,它不同于一些纯数学问题的常规题,往往会配给一些图形,给人比较新颖、有趣的感觉,但题目本身又不会很难,计算、技巧、方法其实要求都不高,以估算、想象、联想为主,它更侧重的是思维的灵活,大局意识、整体把握,不拘泥于局部的某一个细节,有一定的创新性,更符合当下我们培养人才的目标和方向.
与之类似的还有去年的网红高考题(维纳斯的身高问题).
例2 (2019年高考全国Ⅰ卷理科第4 题)古希腊时期, 人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是≈0.618, 称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是( )

A.165 cm B.175 cm C.185 cm D.190cm
解题分析同样这道题从直观上来看是可以估算的.从一个黄金比例出发, 如头顶至咽喉的长度与咽喉至肚脐的长度之比为求出咽喉至肚脐的长度大致为≈0.618⇒x ≈42,总身高约为26+42+105=173cm,比较接近的就是答案C.计算并不复杂,可以非常快速精准的找到答案.但很多同学却陷于精确计算里面了,咽喉与脖子下端有一个长度,肚脐到腿也有一个长度又该怎么算呢?其实此题的目的就是考察学生的直观想象+估算,最后的问题也是“其身高可能是”,说明不需要精确计算.另外从整个人体来看那些小长度可以忽略不计或者凭我们的直观给它一个估值,而从选项来看各个长度差距也比较大,10cm 的误差范围说明也不要纠结于那些不可知的小长度,所以说直观想象+估算用的好,完全可以起到事半功倍的效果.
二、无图有形,想象+逆向
例3(2020年高考全国Ⅰ卷理科第22 题)在直角坐标系xOy中,曲线C1的参数方程为(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为4ρcosθ-16ρsinθ+3=0.
(1) 当k=1 时,C1是什么曲线?
(2) 当k等于4 时,求C1与C2的公共点的直角坐标.
解题分析(1)略.(2)主要是参数方程
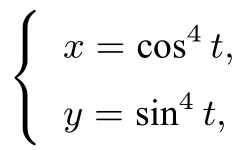
的化简比较困难.可以说这是一道没有图的题目,但有比较工整的“形”—参数方程关于方幂通常我们做的比较多的变形是低次往高次上化,如
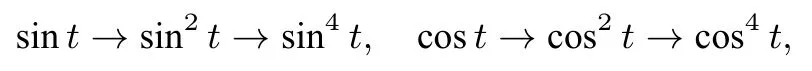
特别是sin4t=(sin2t)2,cos4t=(cos2t)2.
这是很多同学都能想到的,但反过来
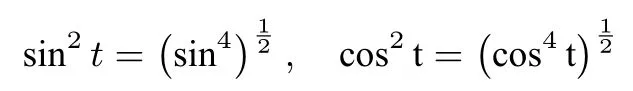
很多同学可能就想不到,所以这道题做不下去基本上就是卡在这个点上.当出现问题的时候不妨多观察一下这个式子的特点,我们说美的式子也是一种图形,并非有图才直观,无图想象也要直观.数形结合、定性分析已经成为高考试题的重要组成部分.反复观察下面的式子:
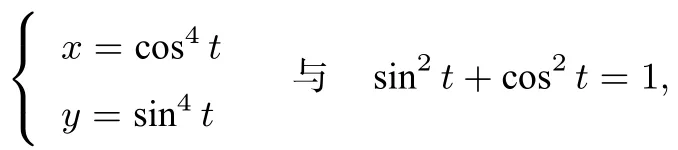
想象一下它们之间的关系
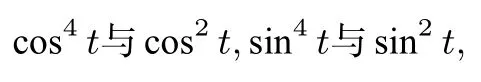
不难想到
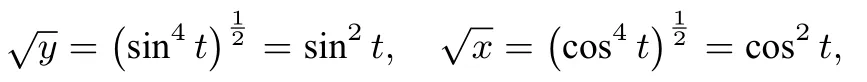
所以
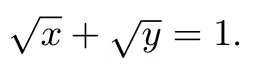
这两个几乎同样的式子显示出的规律其实非常明显,多看几遍不难发现它们之间主要存在平方关系,平方逆运算就是开方.题目的用意就是要我们将四次方式反过来化为二次方式,这里就充分体现了我们老师在讲新课的时候有没有着重渗透平方与开方互为逆运算这样的一种数学思想方法.
逆向思维是我们想象的一个方向,也通常是我们创新能力培养的一个重要途径,如加法与减法、乘法与除法、乘方与开方、导数与积分、三角函数与反三角函数、函数与反函数等等,逆向思维用的好就可以很好的举一反三、触类旁通,更好的加深对概念的认识和理解,更好的把握数量关系和图形特点的本质.该题目的是通过对式子所呈现出来的“形”进行直观想象来触发学生的逆向思维进而实现创新能力的提升,这种变形变式能力也是数学常用的方法技巧之一,此题与2019年高考全国Ⅰ卷理科第22 题有异曲同工之处:
例4(2019年高考全国Ⅰ卷理科第22 题)在直角坐标系xOy中,曲线C的参数方程为(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线ℓ的极坐标方程为2ρcosθ+
(1)求C和ℓ的直角坐标方程;
(2) 求C上的点到ℓ距离的最小值.
解题分析这道题的式子也是一个非常好的“形”,由这个式子可以联想到很多数学公式,如: 平方差公式、完全平方公式、三角函数公式等,所以这道题也有很多巧妙的解法,如:
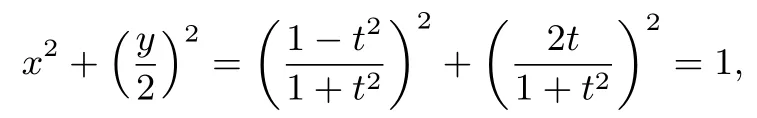
或作三角代换t=用三角万能公式:
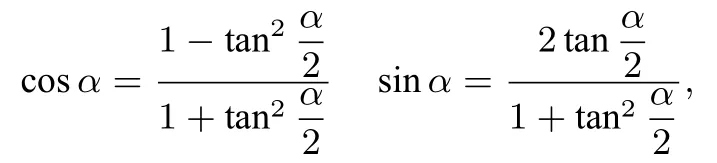
再代入三角函数的公式sin2α+cos2α=1 等.
但如此精巧的解法很多中下层同学很难看出来或根本想不到, 更别说是在紧张的高考考场上了.此时一定不能盲目的去做, 而是要停下来多观察式子的特点, 直观感觉找准切入点—想办法先换算出t, 但两个式子好像都不太好求出t, 其实仔细观察后不难发现上式比较容易先化出然后将t2整体代入下式就可以换出t,再利用t与t2的关系消去参数t,从而得到x,y的直角坐标方程.
这里学生只要明白一个核心观念就可以了: 知道了t2也就等价于知道了t,再把它当做已知量继续代入其他式子就一定能换出t.有了这个“定海神针”作为支撑,哪怕中间步骤繁琐一点,还是有足够的信念坚持能做出来的,相比较想不出巧妙解法而不知从何下手,我觉得这种做法更直观更切实有效.所以说很多时候我们看待数学问题要有整体意识、逆向思维,要更侧重数学思想方法的把握,打开我们僵化的思维、开阔我们的视野,思维的导向往往比方法、技巧更重要.
三、无图无形,直观+猜想
例5(2020年高考全国Ⅰ卷第21 题)已知函数f(x) =ex+ax2-x,
(1)当a=1 时,讨论f(x)的单调性;
(2)当a=1 时,f(x)≥求a的取值范围.
解题分析这道题既没有图也没有形式工整的式子—“形”,但该题大部分同学都知道基本方法是利用导数工具来解决函数的性质问题,沿着这个思路一步步往下做看能发现什么.在做第一小问时
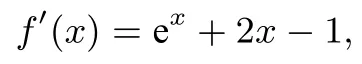
直接观察可以得出该导函数是增函数(因为y= ex和y=2x-1 都是增函数),但找出方程的根有点困难.令
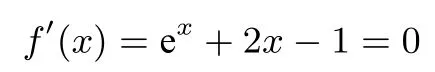
这是一个超越方程, 在中学范围内没有确定的方法求解, 要找出它的根, 就只能靠我们的经验或直观+猜想了,如果把x=0直接代入会发现方程是成立的,所以马上发现0 就是它的一个根, 再结合单调递增的性质可以大致想象出其导函数f′(x)=ex+2x-1,的图象如上图所示.
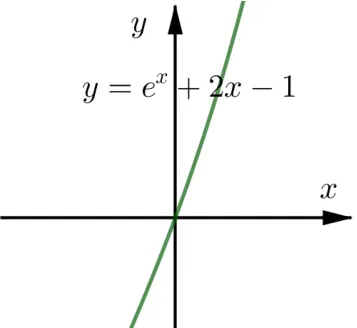
根据导数的图像特征,原来的函数f(x) = ex+x2-x的单调性就很清楚了: 当x >0 时,f′(x)>0,f(x)单调递增;当x <0 时,f′(x)<0,f(x)单调递减.
做第二问时同样也需要直观+ 猜想来助攻.首先将式子分类, 构建出新的函数: 当x= 0 时, 待证不等式恒成立,a ∈R; 当x >0 时,a ≥恒成立, 令h(x) =, 所 以h′(x) = 令h′(x) = 0, 其 中g(x) =- x -1 = 0 的根也需要凭我们的直观观察出来,尝试把x=0 代入进去发现仍然是成立的!(屡试不爽)说明x= 0 是它的一个根,还有没有其他的根? 这个时候就需要用单调性来保证根的唯一性,所以想到需要再进行求导来判断.
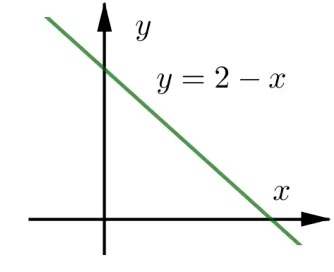
令g′(x) = ex - x -1, 直观发现g′(0) = 0;再次求导g′′(x) =ex -1,当x >0 时,g′′(x)>0,说明g′(x) 单调递增, 所以当x >0时,g′(x)>g′(0) = 0, 说明g(x)也是单调递增, 因此g(x)>g(0) = 0, 因此对于h′(x) =只要考察s(x) = 2-x这部分的正负情况就可以了, 再次借助于它的图象可知: 在(0,2)内,h(x)单调递增; 在(2,+∞)内,h(x)单调递减, 所以h(x)max=h(2)=从而a ≥
整道题的关键点其实还是几个超越方程的求根问题,好像超过我们中学数学的范畴,但实际上凭我们的解题经验和对数学的直观想象一般都能直接看出方程的根,如果不具备这样的核心素养,一味的钻进去求解计算往往最后就做不下去.类似的问题还有下面的这些导数题:
题目1(2019年高考全国Ⅰ卷理科第20 题)已知函数,f(x)=sinx-ln(1+x),f′(x)为f(x)的导数.证明:
(1)f′(x)在区间存在唯一极大值点;
(2)f(x)有且仅有2 个零点.
题目2(2018年高考全国Ⅰ卷理科第21 题) 已知函数
(1)讨论f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2,证明:<a-2.
再如下面的向量题:
例6(2020年全国Ⅰ卷理科第14 题)设a,b为单位向量,且|a+b|=1,则|a-b|=____.
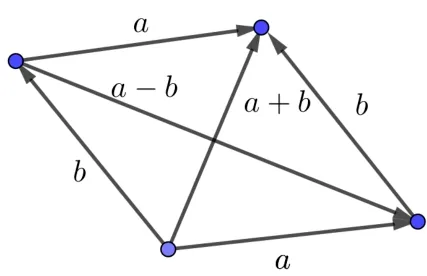
解题分析该题看上去跟图形没有任何关系, 但可以根据数的特点直观想象出图形来.根据|a|=|b|=1,|a+b|= 1 可以想象出一个等边三角形, 再利用向量三角形运算规则马上可以得出|a-b|就是钝角三角形中120°所对的边长能想象出图形出来这道题计算起来也就非常简单.
纵观近几年的高考题不难发现直观想象这一数学核心素养的提升是一个趋势, 无论是数还是形都要求越来越高.有图直观好想象,无图想象也要直观,再利用数形结合、定性分析、全局意识、整体把握、逆向思维、···,往往能达到攻无不克,无坚不摧的效果!事实上我们现在的科研需要有方法有技巧,更需要创新,直观感受往往是创新的起点,再加上丰富的想象和大胆的猜想,最后用我们的逻辑推理、数据分析、数学计算等方法技巧来加以核实和验证从而成就我们的伟大创新和发现.所以说没有很好的直观想象就很难有创新和发现,也就不会有我们今天的科技进步!
