一道函数与导数试题命题历程*——构想、探究、模仿

福建省泉州第五中学(362000) 杨苍洲

函数与导数试题的命制,命题者需要先设定考查的知识载体,及其所需承载的思想方法、学科能力、核心素养等,并根据设想,去构造合适的函数模型.有了函数模型,就可以通过研究该函数的形态与性质,在函数的形态与性质中发现问题,提出问题.命题的过程往往并不是一帆风顺的,此时就需要命题者不断地尝试、调整,也可适时地借鉴成题的命制手法,把它迁移应用于设定的函数背景.

下面展示2020年5月泉州市质检函数导数试题在命题过程中笔者所经历的探究历程.

1 试题与解析

题目1(2020年泉州市5月质检理科) 已知函数

(1) 若f(x)在(0,+∞)单调递增,求a的值;

本小题主要考查函数的单调性与极值、导数的应用等基础知识,考查抽象概括能力、推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想,考查数学抽象、逻辑推理、数学运算等核心素养,体现了综合性、应用性与创新性.

解析(1)f′(x)=(x-a)lnx.因为f(x)在(0,+∞)单调递增,所以f′(x)≥0,即(x-a)lnx≥0.

(i) 当x ＞1 时,lnx ＞0,则需x-a≥0,故a≤xmin,即a≤1; (ii) 当x= 1 时, lnx= 0, 则a ∈R; (iii) 当0＜x ＜1 时,lnx ＜0,则需x-a≤0,故a≥xmax,即a≥1.

综上所述,a=1.

(2)g(x) =+a,g′(x) =因为所以g′′(x)＞0,所以g′(x)在(0,+∞)单调递增.又因为g′(1)=所以存在x0∈(1,e),使g′(x0)=0,且当x ∈(0,x0)时,g′(x)＜0,函数g(x)单调递减;当x ∈(x0,+∞)时,g′(x)＞0,函数g(x)单调递增.故g(x)最小值为g(x0)=

由g′(x0) = 0, 得a=因此h(a) =令τ(x)=x ∈(1,e),则τ′(x) =＞0, 所以τ(x) 在区间(1,e) 上单调递增.又因为且τ(1) =所以1＜ x0＜e, 即x0取遍(1,e) 的每一个值.令φ(x) =lnx(1＜ x ＜e), 则φ′(x) =(2 lnx+3)(lnx-1)＞0, 故函数φ(x)在(1,e)单调递增.又φ(1) = 0,φ(e) =所以0＜φ(x)＜故函数h(a)的值域为

2 设想与命题

在上述试题的命题过程,笔者经历了“构想—探究—模仿”的心路历程,目标明确,过程曲折,终得试题.

2.1 函数模型的构想与调试

命题之初,笔者设想的函数形态: 具有两个极值点,其中一定一动.笔者拟通过比较两个极值点的大小,从而引起讨论,以考查分类与整合的数学思想.并以此函数为背景,设置问题,考查导数的应用.

现设定函数f(x) 的导函数为f′(x) = (x-a)lnx, 则其可能的两个极值点为a,1, 具有笔者所拟定的函数特征.根据导函数, 可以推得, 我们需要研究的函数可以是

2.2 探究函数的形态与性质

根据实数a的不同取值, 可知函数f(x) =的图象可能有下述四种情况.

(1)当a≤0 时,函数f(x)的图象如图1.f(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,f(x)有极小值点1.

(2)当0＜a ＜1 时, 函数f(x)的图象如图2.f(x)在区间(0,a)和(1,+∞)上单调递增,在区间(a,1)单调递减,f(x)有极大值点a和极小值点1.

(3)当a= 1 时,函数f(x)的图象如图3.f(x)在区间(0,+∞)上单调递增,f(x)无极值.

(4)当a ＞1 时,函数f(x)的图象如图4.f(x)在区间(0,1)和(a,+∞)上单调递增,在区间(1,a)单调递减,f(x)有极大值点1 和极小值点a.

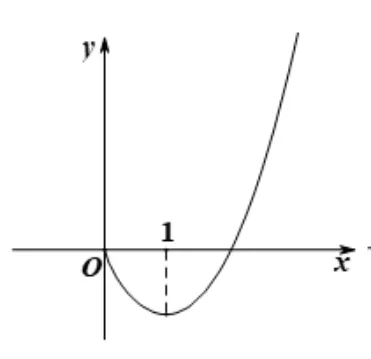
图1

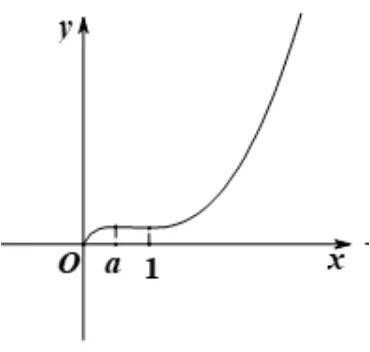
图2

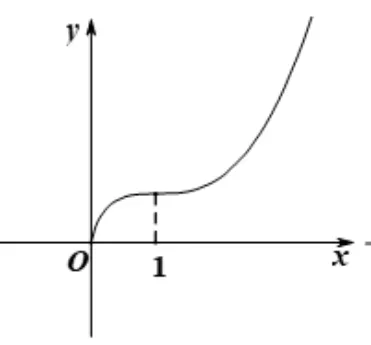
图3

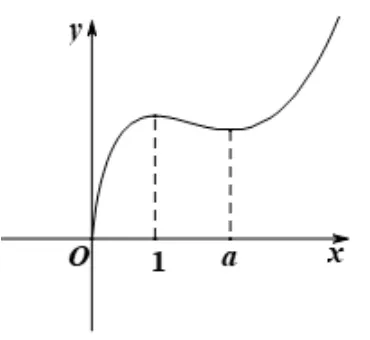
图4

2.3 从函数性态中提出问题

根据函数的图象特征,我们可以提出关于函数单调性、极值的问题.如: (1)讨论函数f(x)的单调区间;(2)讨论函数f(x)的极值;(3)若f(x)在(0,+∞)单调递增,求a的值;(4)若f(x) ≥0,求a的取值范围.上述问题均可作为试题的第一问,在考查利用导数研究函数单调性、极值的同时,也考查分类与整合的数学思想.

如何进一步探究函数的性质,从而使导数的应用更加深入? 我们继续观察函数f(x)的图象.在f(x)存在两个极值点的前提下,我们可以研究两个极值点x=a和x= 1 关于拐点x0(设f′′(x0) = 0)的偏移关系, 如: (1)讨论a+1 与2x0的大小关系;(2)讨论f(a)+f(1)与2f(x0)的大小关系;(3)讨论与f′(x0)的大小关系.

这里列出的几个几何关系,都是基于“极值点偏移”的设问.经过验证,我们发现上述问题或过于简单或过于繁杂,都不是理想的试题设问.因此,只得另辟它径!

2.4 借鉴成题的命题经验

通过观察,我们发现函数f(x)图象上点P(x,f(x))与原点O(0,0)连线的斜率存在最值,因此,我们考虑研究函数的最值问题.

由 于g′(x) =可推得: 当a ＞0时, 存在x0∈(0,+∞), 使g′(x0) = 0, 且当x ∈(0,x0)时,g′(x)＜0, 函数g(x) 单调递减; 当x ∈(x0,+∞)时,g′(x)＞0, 函数g(x) 单调递增.g(x) 的最小值为

探究的思路碰壁了,似乎难以为继! 此时,我们可以考虑借鉴成题的命题手法并迁移应用.此处,笔者借鉴了2016年全国Ⅱ卷理科数学第21 题第(2)步的命题思路.

题目2(2016年高考全国Ⅱ卷理科第21 题)

(Ⅰ)讨论函数f(x)=的单调性,并证明当x ＞0时,(x-2)ex+x+2＞0;

(ⅠⅠ)证明: 当a ∈[0,1)时,函数g(x)=0)有最小值,设g(x)的最小值为h(a),求函数h(a)的值域.

题目2 的第(2) 步中, 求解可得: 存在x0∈(0,2], 使g′(x0) = 0,且当0＜x ＜x0时,g′(x)＜0,函数g(x)单调递减;当x ∈(x0,+∞)时,g′(x)＞0,函数g(x)单调递增,故g(x)最小值为g(x0)=

与上述的探究结果相仿.那么,题目2 是如何让探究继续的呢? 由g′(x0) = 0,可得到a与x0的关系,进行消元后,g(x0)可化为g(x0)=而后通过限制a的范围,实现对x0的范围进行限制(此处需保证a与x0是一一对应的),从而可以继续研究g(x0)的取值范围,即研究g(x)的最小值g(x0)的取值范围.

现在回到我们的研究进程, 模仿上述命题的证明手法.由g′(x0) = 0,得因此g(x)的最小值g(x0) =又因为g′(1) =-a+,g′(x)在区间(1,e)上单调递增,因此,只需设定即可使得x0取遍(1,e)的每一个值.

3 结束语

命题不易! 命题有趣! 命题是一件创造性的工作! 命题是一次深刻的学习!