基于超网络的舆论演化动态模型

王志平,王 佳

(大连海事大学理学院，辽宁 大连 116034)

0 引言

随着社会网络的逐步发展，人们越来越关注舆论，通过微博、新闻、浏览器等可以了解世界各地的事情发展，并且时时刻刻关注着他们的发展变化。因此，舆论演化逐渐成为一种不可忽视的频发性社会现象，研究舆论传播的发展变化规律具有很重要的现实意义[1-2]。

舆论传播是指社会公众在特定事件下发表个体意见以及意见之间相互作用形成的观点。网络舆论传播是指人们通过网络对一些事情公开表达的意见或态度。哈贝马斯曾经说过：“束缚舆论传播就等于否定民主，与其说适合民主法治国家，不如说适合开明专制下的极权主义福利国家；一切为了人民，但一切都没有经过人民”。随着社会的发展，在我们这个民主的社会主义国家，从每个人的小事到国家大事，人们都可以通过网络公开表达自己的意见或建议，所以人们对舆论传播的关注也越来越多，同时也吸引了越来越多学者进行研究。

网络随处可见，因此网络舆论的传播成为越来越多学者的研究对象。目前已有不少学者对舆论进行了模型构建和仿真分析，且涉及的因素是固定的，如节点的添加率、形成的超边数、重组超边数等，为了更贴合实际，本文对模型进行了一些改进：1)提出了一种基于非均匀超网络的舆论动态演化模型，解决了网络节点及其超边老化的问题。模型的构建包括4个过程，即新超边的形成、新节点的加入、超边的重链以及节点及其超边的老化。2)在上述基础上，对不确定因素进行了随机化，即对增加节点的数量，形成超边的数量，选择进入超边的新节点数量(也就是说，每一批节点被选择进入超边存在一定概率，并不是所有的节点形成一个超边)，节点本身的关注和影响、节点之间的影响等等进行随机化处理。3)同时，通过Matlab程序仿真，本文分析了10个参数对模型的影响，如节点的个数、节点本身的关注程度、节点之间的影响、选择进入超边的新节点个数以及超边中的旧节点个数等。我们得到了平稳平均超度分布服从幂律分布，其中节点表示关键词，超边表示由关键词构成的话题。

1 理论背景

舆论的演化在很早的时候就受到了人们的关注，最早可以追溯到1956年，French建立了一个简单的离散数学模型去研究团体的行为复杂性[3]。在1981年，Lehrer和Wagner[4]将有限理性作为从公平到认识论在舆论建模过程中的基本条件。在物理的视角中，最早是1925年，伊辛提出了研究铁磁体的一种最简单模型，2000年，Sznajd基于物理学描述磁极旋转的伊辛模型是描述二元观点相变的最早常用舆论动力学模型，在此基础上，出现了不少以此为基础的模型与相关的研究成果[5-9]，包括Sznajd观点动力学模型的相变现象、小世界网络、无标度网络上的演化特性等。此外，舆论的模型存在很多种形式，熊莲花等人[10]在“优先占有”的理论基础上建立了舆论的演化模型；何建佳等人[11]借鉴Hegselmann-Krause模型粒子交互的建模思想，构建了扩展Hegselmann-Krause模型；胡祖平等人[12]在元胞自动机的基础上对舆论的演化进行了仿真分析。同时，人们也研究了各种因素下的舆论演化发展[13-18]，以此更加贴近现实生活。

随着社会的发展也有不少学者在复杂网络的基础上对舆论的演化进行了模拟仿真等[19-21]。而超网络是继复杂网络研究热潮之后，研究者关注的另一个重要方向，超网络是较通常意义上的复杂网络更为复杂的网络，该网络的每一条超边都能连接任意多个节点的特性使其能够比复杂网络更好地描述真实世界中的复杂系统。所以舆论的演化模型在之后的发展中逐步从复杂网络过渡到了超网络的研究上。

Wang等人[22]提出了一种进化超网络模型；李倩倩等人[23]基于超网络研究了社会舆论的演化；浦娇华等人[24]在动态模型的基础上构建了舆论演化模型；Chang等人[25]对SPL分布进行了一个详细分析使人们对幂律分布有更深刻的认识；马涛等人[26]对节点的退出机制进行了一定的研究，通过建立M-G-P模型与理论分析发现度分布符合幂律分布。张峰等人[27]基于决策偏移构建了舆论动力学模型；Li等人[28]研究了媒体在舆论的演变中起到了什么作用，因此构建了媒体影响下的舆论动态数学模型。Wang等人[29]在超网络的基础上提出了双层超网络模型，更加有效地反映了实际情况；Guo、Yin等人[30-31]基于超网络构建了非均匀网络模型，并且通过理论分析即仿真模拟得到其结果符合幂律分布。

2 基本概念

2.1 复杂网络

到目前为止，复杂网络并没有一个具体的定义，但是存在两种定义来解释它。钱学森给出了一个这样的定义：“具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络。”而维基百科中定义复杂网络为由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构。

2.2 超网络

超图是比图更为复杂的一种图形，它可以包含任意个节点数目[32-33]，因而更加贴合现实生活。设V={v1,v2,…,vn}为有限集Ei={vi1,vi2,…,vij}(vik∈V,k∈N*)是V的非空子集族，Eh={E1,E2,…,Em}表示超边集，那我们就定义H={V,Eh}为超图。超网络[34]就是由超图描述的复杂系统。

2.3 非均匀网络

传统的超网络模型都是均匀的，即超边中只包含两个节点，而非均匀网络是指在一个度分布具有适当幂指数的幂率形式的大规模无标度网络中，绝大部分节点的度相对较小，只有少数节点的度相对较大。非均匀的超网络的一个明显特征是每一个超边中都可包含任意数目的节点。

3 模型构建

本文基于超网络构建了一种非均匀的动态演化模型，且模型中变量符合一定的分布，使得变量具有随机性，更加贴合现实生活。本文中节点代表关键词，超边代表关键词形成的话题。

在模型中，对参数的应用如下：

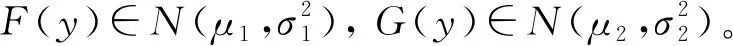
T时刻时，一个新的节点连接到第i批的第j个节点的概率为ω，与该节点的超度hj(t,ti)，自身的关注度ξi及节点连接后产生的影响yi成正比。即

(1)

其中,ti表示第i批节点到达网络的时间，hj(t,ti)表示第i批节点的第j个节点在时间t的超度。

在舆论传播的演化中，本文构建的模型分为4个部分：1)添加新的超边。即现有的关键词形成了新的舆论(如中国、湖北、新冠肺炎等)。2)重新连接链路。即旧的舆论消失且与其他关键词构成新舆论(如旧关键词中国、巴基斯坦等)。3)添加节点。即产生新的关键词，从而与现有的关键词形成新的舆论(如新关键词多省市清零与旧关键词新冠肺炎等)。4)节点及其超边的老化。即舆论的热度衰退，且关键词淡出视线或者人为因素使得关键词及其话题淡出人们的视线。

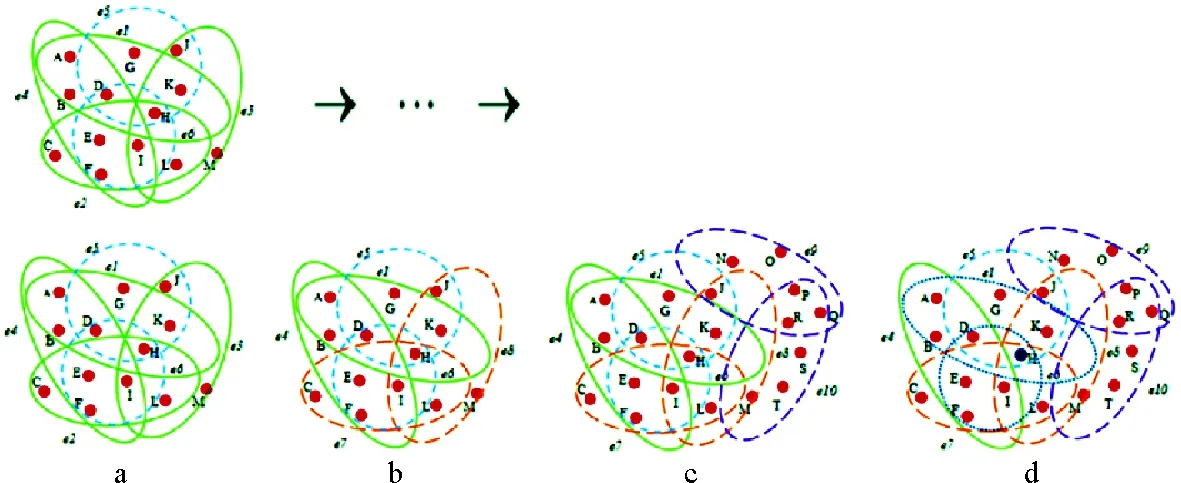
图1 舆论演化模型示意图

模型的初始节点的数量为m0=13，节点A～M，且存在4个超边(e1～e5)。在每个时间t，都会以一定的概率发生以下4个过程：1)添加新的超边。在初始图中，随机选择一个节点H，与D、G、k、J形成新的超边e5；与D、E、F、I形成新的超边e6。2)重新连接链路。随机选择一个节点I，删除节点I的一个超边e3，与J、K、H、L、M形成新的超边e8；删除超边e2，与C、E、F、H、L形成新的超边e7。3)添加节点。T时刻时，进来一批新的节点N、O、P、Q、R、S、T，m1=7，选择原来的(m2=1)个旧节点与新节点当中的其中一部分(m11=5)个形成新的超边，如图所示e9，e10为所形成的新的超边。4)节点及其超边的老化。随机选取一个节点H，老化节点H所在的超边(e1，e6)与节点H，且不再形成新的超边。

4 理论分析

假定原始超网络中的节点总数为N，根据本文第4部分的模型，可以得到如下动态方程：

(1)以概率p将m个超边添加到原有的超网络中

(2)

其中，m服从参数为λ2的泊松分布，旧节点的个数u服从参数为λ3的指数分布。右边第一项表示现有节点的随机选择，第二项表示以一定概率对旧节点的选择。

(2)以概率q重新连接m个超边

(3)

其中，右边第一项表示要删除超边的节点的随机选择，右边第二项表示重新连接超边的节点的选择。

(3)以概率r老化节点及s个超边

(4)

其中，右边的式子表示要老化的节点及其超边的随机选择,选择更一般的老化模型[35-36]。

(4)将m1个节点以概率1-p-q-r添加到现有的超网络中，随机选择m11个新的节点与m2个旧节点以概率ω形成超边

(5)

右边式子表示被选择进入新超边的节点数是以一定的概率选择的。

根据以上4个等式，可以得到舆论传播的演化机制服从如下动态方程:

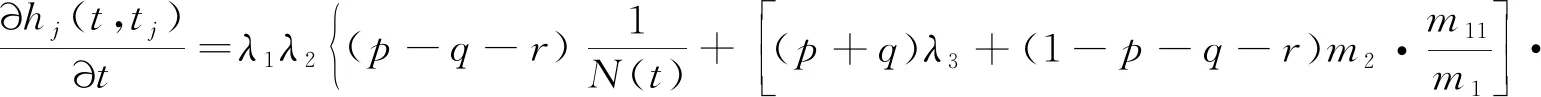
(6)

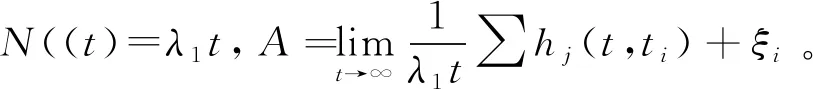
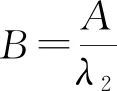
(7)

对式(7)进行简单的积分，可以得到

(8)

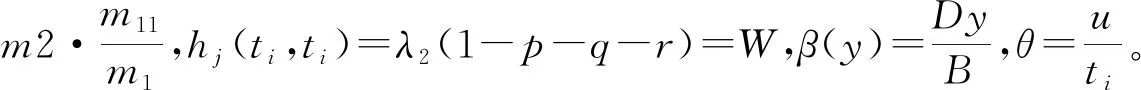
为了简便计算，将节点的老化过程进行简化，即只选择一个节点所在的超边进行删除，可得：

(9)

从而得到该过程的超度：

(10)

根据式(10)，可知

(11)

由上文可知节点的到达速率是服从泊松分布的，节点到达的时间遵循伽马分布，因此，可以得到等式(12)：

(12)

由式(10)可知，节点超度的概率公式如(13)：

(13)

于是，得到平稳平均超度分布的概率为

(14)

根据式(10)，还可知

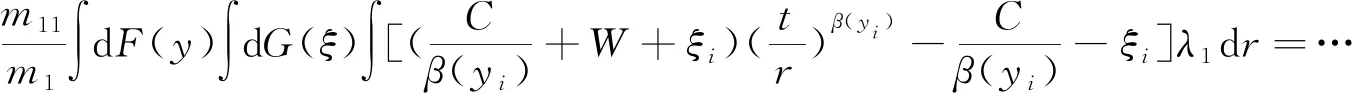
(15)

对式(15)进行化简，得到

(16)

其中B是由以下积分来确定的，即

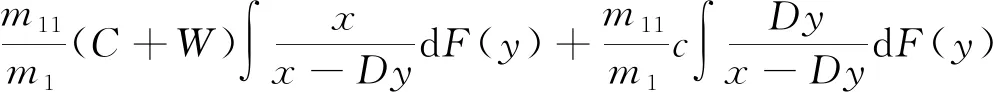
(17)

把式(17)称为具有自身关注度与节点间影响力的特征方程。

接下来对式(17)中的参数进行分类讨论：

1)ξi=0,yi=1，本文的模型将退化为简单模型，且有如下结果:

(18)

其对应的特征方程为

其中，Q=λ2[(p-q)(λ3+1)+(1-p-q-r)(m2+m11)]。特征方程的解为

(19)

其中，L=Qm1-m11(C+W)。

可以得到平稳的平均超度分布为

(20)

2)当ξi=1,yi=a时，有

(21)

从而得到：

(22)

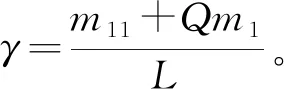
3)当yi=1,ξi=a时，得到：

(23)

然后可以得到:

(24)

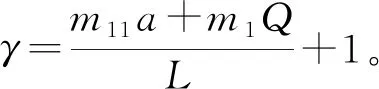
4)当ξi=a1,yi=a2时，得到特征解：

(25)

然后可以得到平稳的平均超度:

(26)

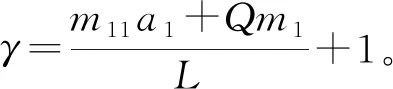
在此之前有人提出SPL，当p(k)∝(k+α)η，其中η和α是常量，SPL是从幂律分布到指数函数的分布，其中α表示分布偏离幂律的程度，数值越大，偏离幂律越大[37]。根据本文的分析可以知道，模型退化为简单模型时，是完全符合幂律分布的；当本文的模型参数为任意数值时，其结果显示仍是完全遵循SPL的。

5 模拟数值

针对上述结果，利用Matlab程序进行了合理的模拟。这里每个模型都进行了多次运行，之后选取效果最好的结果。此外，由于模型中大部分的变量都是随机的，所以针对每一个变量都有其模拟结果。其中k表示节点的超度，p(k)表示超度为k的概率，k的取值范围与超网络的规模以及动态演化过程相关。模型中的参数及其表示意义如表1所示。

表1 参数及其意义

5.1 参数N的影响

如图2所示，当p=0.15，q=0.15，r=0.25，m1=5，m=9，u=10，m11=4，y～N(5,5),ξ～N(10,10)时，其中m1是服从参数a1=5的泊松分布，m是服从参数a2=5的泊松分布，u是服从参数a3=10的指数分布，m11是服从a4=3的指数分布。令N=20 000、30 000、50 000。根据结果能够看到，当k到一定数值时，随着N的变大概率随之变小，这说明有限个关键词被包含在同一个舆论内很少有舆论可以包括所有的关键词。即关键词具有一定的针对性，可以形成不同的舆论。

5.2 参数y、ξ影响

如图3所示，当m1=5，m=9，u=10，m11=1，p=0.15，q=0.05，r=0.25，ξ～N(10,10)，N=15 000，其中λ1～p(5),λ2～p(5),λ3～Exp(10),λ4～Exp(3)。此时对u1进行改变，分别为5、10、15。由图3可以看到，当k一定时，图像整体随u1的增大而向下移动，即节点相连对舆论的形成存在一定的影响，当连接的节点越多或者节点间相关性越高时，对舆论的限制越大，从而更难形成新的舆论。也就是说，二者之间影响越大可以形成新舆论的概率越小。当k达到一定程度时，其特征不再明显，此时节点所表示的意义有限制，只有特定节点连接存在特殊意义。如当关键词‘高考’与‘作弊’相联系所形成的超边的超度是小于‘高考’与‘省份’相联系所形成的超边的超度，节点间的影响力不同，那么对节点的超度是存在一定影响的。

如图4，对u2进行改变，分别为10，20，30。当m1=5，m=6，u=8，m11=2，p=0.15，q=0.05，r=0.25，y～N(5,5)，N=15 000，其中λ1～p(5),λ2～p(5),λ3～Exp(10),λ4～Exp(3)。当k较小时，随着u2的增大概率逐渐增大，此时超网络的超度分布仍具有幂率分布；当k超过一定的范围时，随着u2的增大，其节点幂率特征不再明显。即节点的超度在一定范围内随它自身的关注度的大小而变化，当超过一定的范围时，其超度不再随着关注度的变化而产生规律性改变。

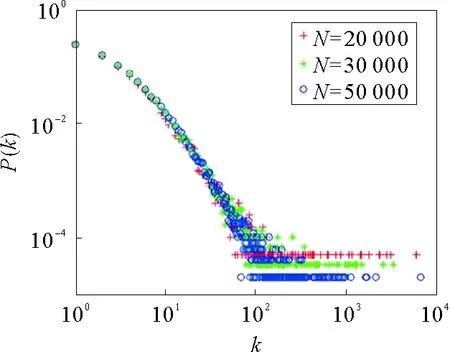
图2 参数N影响示意图

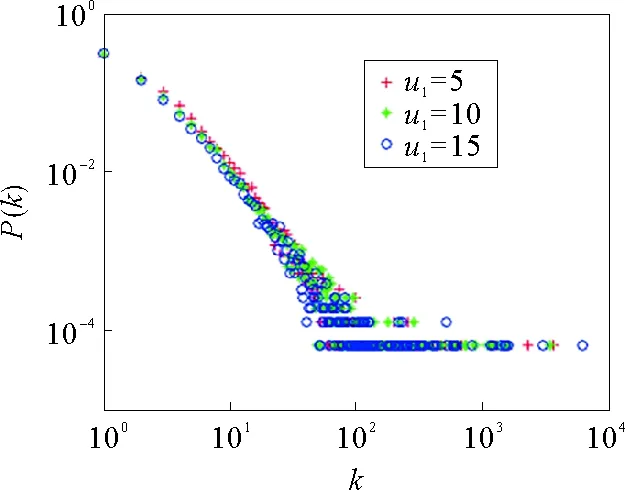
图3 参数u1的示意图

图4 参数u2的示意图

5.3 参数p、q、r的影响

当m1=9，m=6，u=3，m11=1，q=0.05，r=0.25，y～N(5,5),ξ～N(10,10)，N=15 000时，其中λ1～p(5),λ2～p(10),λ3～Exp(10),λ4～Exp(3)。如图5所示，当p增大时，图像整体向右移动，即关键词与话题相关性越强时，那么可形成的话题范围越多。当k一定时，可以看到，添加超边的概率越大，其节点超度为k的概率越大，即同一k值下超度形成概率越大。

当m1=8，m=14，u=9，m11=2，p=0.05，r=0.15，y～N(5,5),ξ～N(10,10)，N=20 000时，其中λ1～p(5),λ2～p(10),λ3～Exp(10),λ4～Exp(3)。从图6中可以看到，随着q的改变其图像无明显变化，从而q对于结果没有很大的影响。即当前关键词现在所属的舆论消失与新的关键词组成新的舆论，因此，q不会对其概率产生规律性的影响，其结果反映了网络舆论系统的稳定性。

如图7，当m1=5，m=9，u=10，m11=1，p=0.15，q=0.05，y～N(5,5),ξ～N(10,10)，N=15 000时，其中λ1～p(5),λ2～p(5),λ3～Exp(10),λ4～Exp(3)。从图中可以看出整体图像随着r的增大而下移，即节点消失的概率越大，那么可形成超边的概率越小。即随着话题热度的衰退，其热度降低，从而使得舆论保持在一个稳定水平，其结果与超边的添加恰恰相反，也进一步反映出了网络舆论系统的稳定性。

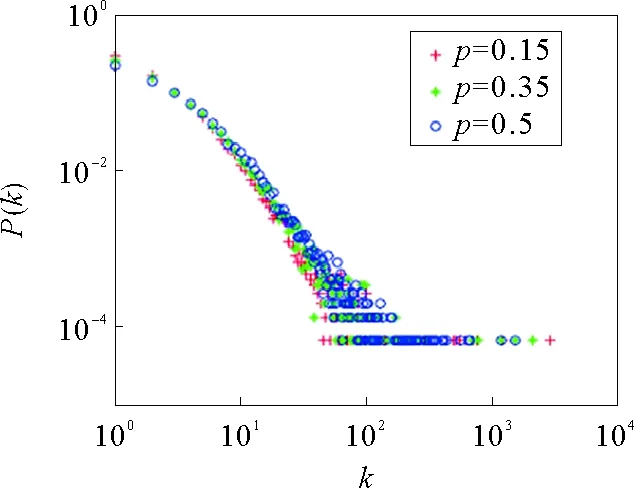
图5 参数p的示意图

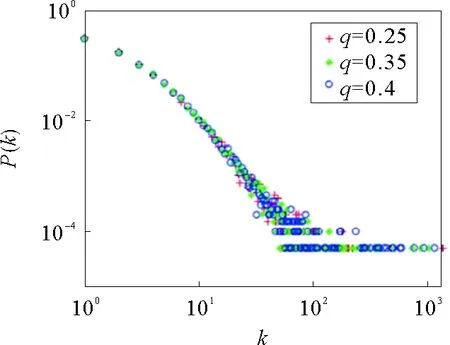
图6 参数q的示意图Fig.6 The parameter q

图7 参数r的示意图

5.4 参数λ1、λ2的影响

当m=6，u=15，m11=5，p=0.05，q=0.1，r=0.15，y～N(5,5),ξ～N(10,10)，N=20 000时，其中λ2～p(5),λ3～Exp(10),λ4～Exp(3)。如图8所示，图像随着参数的增大整体左移，节点的到达速率增大，即节点活跃性增大使得形成更多不同的话题、选择性增多，因此，其关键词的超度并不会随参数的增加而增大，与之相反，节点可形成超边的个数概率越小。

当m1=4，u=15，m11=3，p=0.05，q=0.1，r=0.15，y～N(5,5),ξ～N(10,10)，N=20 000时，其中λ1～p(5),λ3～Exp(10),λ4～Exp(3)。从图9中可以看到，图像不随着参数的变化产生规律性的变化，即节点的超度在于与节点相关联所构成超边数目的多少，仅超边数目的增多表明话题有更大可能的形成性，与节点超度无直接联系，m的改变更多是对矩阵的规模的影响。

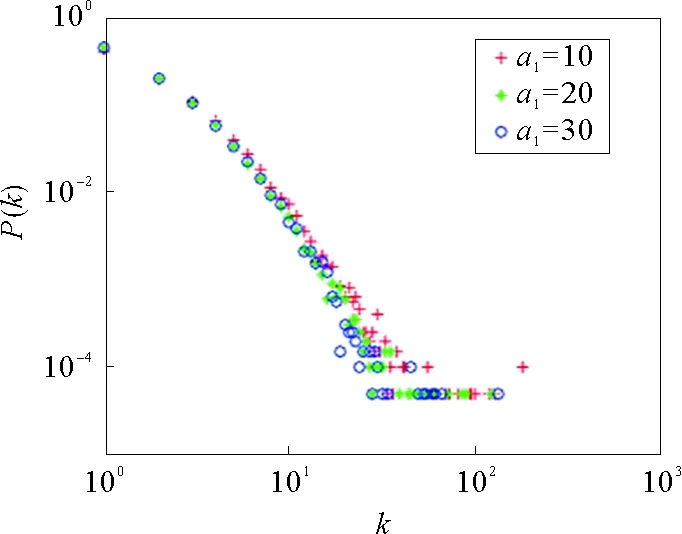
图8 参数a1的示意图

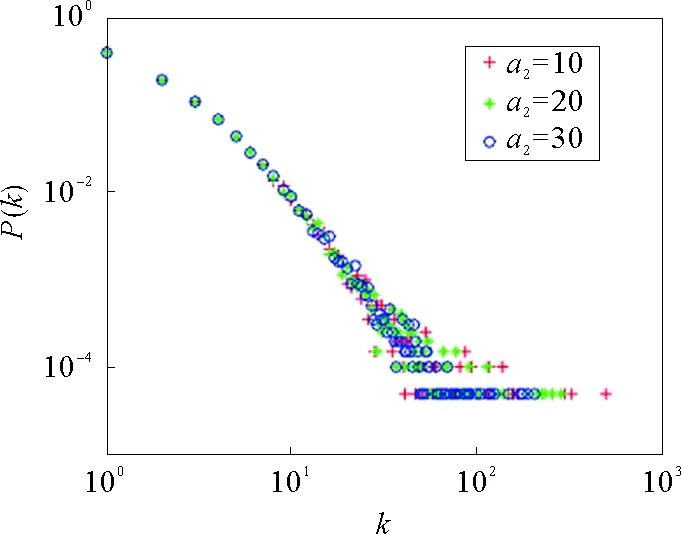
图9 参数a2的示意图Fig.9 The parameter a2

5.5 参数λ3、λ4的影响

当m1=4，m=3，m11=2，p=0.05，q=0.25，r=0.15，y～N(5,5),ξ～N(10,10)，N=20 000时，其中λ1～p(5),λ2～p(5),λ4～Exp(3)。从图10可以看到，随着参数的增大，图像整体下移。超边中旧节点的个数，即形成新超边选择的旧节点个数。当k一定时，随着参数的增大概率减小，即节点个数增多代表关键词增多，从而可形成的话题增多，即选择性增大使得节点超度不随之增大。

当m1=6，m=5，u=4，p=0.05，q=0.1，r=0.15，y～N(5,5),ξ～N(10,10)，N=20 000时，其中λ1～p(5),λ2～p(5),λ3～Exp(10)。如图11，图像整体向右移动，当k一定时，概率随着a4的增大而增大。新节点被选择形成新的超边，超度的规模随之扩大，即节点被选择的概率越大，那么更大可能形成新的超边。

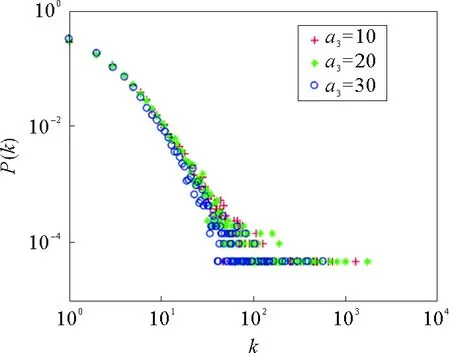
图10 参数a3的示意图

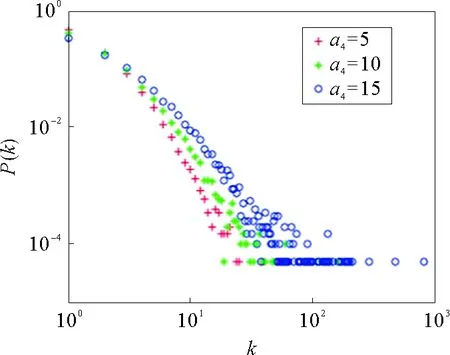
图11 参数a4的示意图Fig.11 The parameter a4

6 结论

本文将超网络与舆论演化结合，通过构建4个动态过程更好地反映了舆论演化的发展变化，且在理论分析的支持下得到其结果是符合幂律分布的。同时，本文构建的模型另一特点就是，通过对现实生活中不确定因素的分析来观察超度的变化。我们使用Matlab对10个参数进行了模拟分析，并且详述了参数对模型的影响，更好地对模型进行了一个阐述。本文的模型可以反映大多数真实系统的结构特征，在很多模型中是通用的。

未来的研究方向为：1)本文中节点的选择是随机的，但在现实生活中每一个节点并不是随机出现或者消失的，不同的节点有不同的被选择概率。因此，在节点的选择这个方向可以进行进一步的研究。2)舆论传播的发生存在周期性，并且其节点的范围与周期相关，所以可以再进一步考虑其周期性。3)当突发性的情况发生时，舆论传播会有很大的变化，因此，进一步的研究可以集中在网络的鲁棒性上。4)节点的老化及其所在超边的老化并不是简单的随机老化，而是存在一定规律的，因此需要进一步的优化。