财政支农对农业技术效率的影响研究

王丹亚，高齐圣

(青岛大学经济学院， 山东 青岛 266061 )

0 引言

近年来，为解决“三农”问题，实现农业经济的持续稳定发展，中国政府出台了一系列财政支农政策，财政支农支出的总体规模在不断扩大，数据显示，财政支农支出从2010年的8 129.58亿元，增长到2019年的22 420.11亿元，年均增长10.68%，与此同时，农林牧渔业总产值也有大幅增长，从2010年的67 763.13亿元，增长到2019年的123 967.94亿元。财政支农支出作为农业经济重要的物质基础，不仅可以作为投入要素直接影响农业经济增长，还可以通过影响农业技术效率间接影响农业经济增长[1]。随着农业资源环境约束的增强和农村或农业劳动力等生产要素持续流向城镇或其他行业，依靠物资资本和劳动力等要素驱动农业经济增长的方式不具有可持续性，在此背景下，农业技术效率在未来农业经济发展过程中将扮演着重要作用[2]。

技术效率的概念最早是由Farrell在1957年提出的，考虑了经济中大多数生产者不能达到最优生产效率的现实情况[3]。随机前沿生产模型最初是由Aginer等以及Meeusen等在1977年分别独立地提出，该模型同时考虑了技术无效率与随机因素对产出的影响，并对技术无效率项和随机扰动项设定了特定的分布，从而可以根据误差项的假设分布估算出技术效率水平，若存在外生变量可以解释技术无效率项时，还可以适当放松部分假设条件[4]。最新研究中，Lai和Kumbhakar提出以生产函数和成本最小化一阶条件为系统，利用最大似然法对整个系统进行估计，同时估算出了技术效率和配置效率[5]，随后，Kumbhakar和Tsionas以此为基础，研究了模型中存在外生变量的情况下对技术效率和配置效率的影响。

在现有文献中，研究外生因素对技术效率影响的方法主要有两步法和一步法两类。刘佳、余国新[1]基于随机前沿生产函数利用一步估计法分析了2000～2011年地方财政支农支出对农业技术效率的影响，发现财政支农支出对农业技术效率具有正向影响。张海鑫、杨刚桥[6]基于随机前沿超越对数生产函数利用一步估计法研究了耕地细碎化、劳动力受教育程度、农业政策等因素对农业生产技术效率的影响，发现耕地细碎化不利于技术效率的提高，种粮补贴对农户的生产技术效率具有正向影响。唐建和Jose Vila[7]基于随机前沿生产函数利用两步估计法研究了1990～2013年间财政支农支出、家庭经济水平、家庭人口规模和劳动力未受教育程度等因素对粮食生产技术效率的影响，发现财政支农支出总体上表现为对技术效率具有促进作用，但在各省市中呈现出明显的差异。Boubacar S B等[8]基于随机前沿生产函数利用一步估计法以几内亚为例研究了户主、务农经验、非农收入、家庭规模等对水稻生产技术效率的影响，发现家庭规模等对技术效率具有正向效应。王亚飞等[2]基于DEA-Malmquist指数法利用两步估计法研究了24个省市的农业外商直接投资对技术效率的影响，发现外商直接投资增加可以促进技术效率改善，但两者之间存在倒U型关系。周鹏飞等[9]基于DEA-Malmquist指数法利用两步估计法研究了财政支农、城镇化水平、工业化程度、农村公路密度等因素对农业技术效率变化的影响，发现财政支农对农业技术效率改善具有正向效应。

随着财政支农体制机制改革的不断推进，现代农业产业技术体系不断调整优化，以国家农技推广机构为主导，农业科研院校、社会化服务等广泛参与、分工协作的农技推广体系不断完善，农业技术推广和扩散的速度逐渐加快，势必会对农业技术效率产生一定的影响。然而，目前关于研究财政支农与农业技术效率的文献相对较少，而且数据较陈旧。因此，本文采用2002～2017年31个省市的面板数据，运用随机前沿超越对数生产函数测算出农业技术效率，实证分析了财政支农支出等因素对农业技术效率的影响，并提出相应的政策建议。

1 研究方法

1.1 模型设置

技术效率(TE)衡量了某生产单位在既定技术水平和投入规模下，实际产出与生产前沿面上可能最大产出之间的垂直距离，距离越大，说明技术效率水平越低，反映了生产者产出能力、资本利用效率和成本控制等特征[10]。目前测度技术效率的方法主要有参数法和非参数法两大类，非参数方法主要以数据包络法(DEA)为代表，该方法主要利用线性规划技术，不需要考虑生产函数，能直接处理多产出情况，但无法考虑随机因素对产出的影响。参数方法主要以随机前沿法(SFA)为代表，该方法需要首先设定生产函数，因采用极大似然估计法估计参数，其计算结果较为稳定，不易受异常值的影响[11-12]。参考Battese和Coelli的研究[13]，随机前沿生产函数的基本形式为

(1)

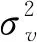
得到TEit后，为进一步考察外生因素对技术效率的影响，设置技术效率影响因素模型的一般形式为[14]

TEit=F(Zit,δ)+εit

(2)

其中，Zit=(1,Z1,Z2,…,ZM1)表示M1个外生解释变量，δ=(δ0,δ1,δ2,…,δM2)表示待估系数，εit为误差项。

1.2 模型参数估计

在模型(1)中，由于存在复合误差，普通最小二乘估计失效，为得到有效且一致的估计量，使用极大似然法进行估计。具体估计步骤如下[13]。

根据Vit服从正态分布，Uit服从截断正态分布，两者之间相互独立的假设，可以得到两者的联合概率密度函数，令Ei=(Ei1,Ei2,…,EiT)′，Ui=(Ui1,Ui2,…,UiT)′，进而可以求出Ei与Ui之间的联合密度函数：

(3)

其中，ei，ui分别为随机变量Ei，Ui的值。因此，Ei的边际密度函数为

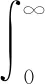
(4)

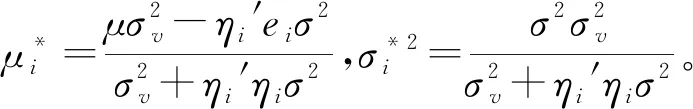
根据Ei与Ui的联合概率密度函数和Ei的边际密度函数，可以得到Ui的条件概率密度函数：

(5)

最终得到技术效率的测算公式为

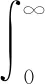
(6)

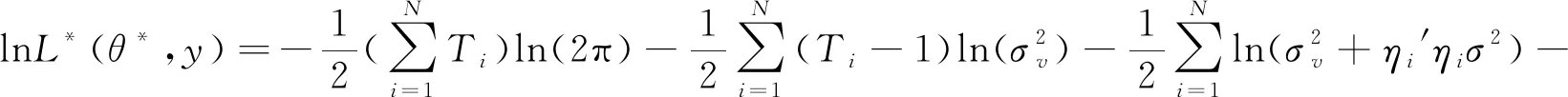
(7)

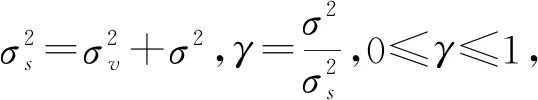
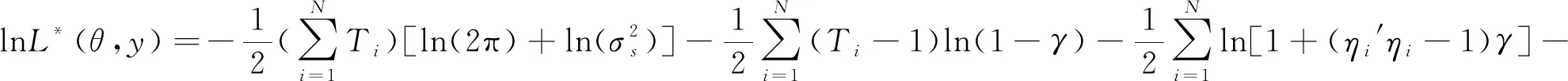
(8)

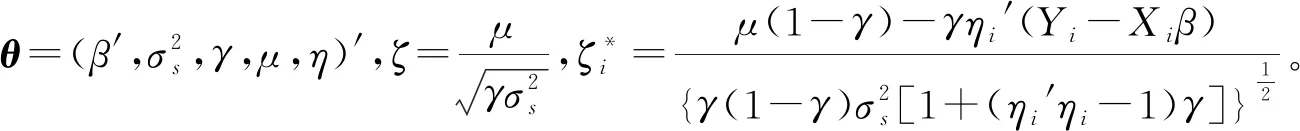
2 数据说明和模型构建

2.1 数据选取及说明

本文研究所用的数据来源于历年《中国统计年鉴》、《中国农村统计年鉴》、《中国固定资产投资统计年鉴》及各省统计年鉴，样本范围是31个省市，样本的时间从2002～2017年，基期为2002年。

随机前沿生产函数中农业产出(Y)采用广义的农林牧渔业总产值，利用农林牧渔业总产值指数对农林牧渔业总产值进行平减，剔除价格因素的影响。投入要素选取劳动力(L)和资本(K)两种生产要素。劳动力投入用第一产业从业人员数进行衡量，黑龙江省2011～2013年数据缺失，采用三次样条插值法进行补缺处理。资本投入用农业资本存量来表示，国内外大多数学者都采用永续盘存法来计算资本存量。永续盘存法计算公式为[15]

Kit=Iit+Kit-1(1-δit)

(9)

式(9)一共涉及到4个变量：一是当年固定资产投资Iit，采用农林牧渔业固定资产投资进行衡量，二是固定资产投资价格指数，用来平减固定资产投资，消除价格因素的影响，采用农业生产资料价格指数进行平减，三是经济折旧率δit，农业资本折旧率采用吴方卫计算的0.054 2[16]，四是基年资本存量Ki0，采用国际上通用的做法，用基年2002年固定资本投资与上样本期间各省区投资增长的几何平均数加上折旧率的比值进行衡量[17]。

技术效率影响因素模型的核心解释变量为财政支农(zn)，用财政支农支出占财政支出的比值进行衡量。由于财政支农的统计指标在不同年份发生了较大变化，借鉴朱万里、胡瑜杰[18]的做法，2002年的数据选取农业综合开发支出，2003～2006年的数据为农业支出、林业支出和农林水利气象等部门的事业费支出之和，2007～2017年选取农林水事务支出。控制变量包括城镇化水平(czl)、灌溉基础设施(ggl)、自然灾害水平(szl)及人力资本水平(jy)4个变量，用城镇人口数占总人口的比值表征城镇化水平，有效灌溉面积占农作物总播种面积的比值表示灌溉基础设施情况，受灾面积占农作物总播种面积的比重表示自然灾害水平，受教育年限表示人力资本水平。

2.2 模型构建

随机前沿生产函数模型中常用的生产函数主要有柯布-道格拉斯和超越对数两种形式，由于柯布-道格拉斯函数假定技术中性和产出弹性不变，而超越对数生产函数形式更为灵活，能更好地避免由于函数形式误设而带来的估计偏差[19]。因此，本文采用随机前沿超越对数生产函数进行测算技术效率，模型的具体形式为

(10)

其中，Yit表示第i省市在t时期的农业产出，Kit表示第i省市在t时期的资本投入，Lit表示第i省市在t时期的劳动投入，TEit表示第i个省市在t时期的农业技术效率，t表示时间项，znit表示第i省市在t时期的财政支农，czlit,gglit,szlit,jyit分别表示第i省市在t时期的城镇化水平、灌溉基础设施、自然灾害水平、人力资本水平，其余变量和误差项定义与前文相同。

3 模型结果分析

3.1 农业技术效率的测算结果

本文采用两步法估计农业技术效率及影响因素，随机前沿生产函数估计结果如表1所示。可以看出γ估计值为0.995 4，十分接近于1，且在1%水平下显著，说明技术无效率项的方差对复合误差的方差影响较大，使用随机前沿分析法是比较合理的。模型的对数似然函数值和似然率LR值都非常大，远大于1%显著性水平下的临界值，拒绝增加约束条件引起模型变动的原假设，表明模型整体可靠。

从模型估计系数来看，农业资本一次项为正和二次项为负但不显著，农业劳动力一次项和二次项均为负，且在5%水平上显著，农业资本和劳动力的交叉项为正，且在1%水平上显著。时间变量的一次项为正但不显著，二次项系数为-0.002 3，在统计学意义下接近于0，这说明在样本选择期间内不存在显著的技术进步影响，故以下主要考虑财政支农对农业技术效率的影响。

根据估计结果，可以得到2002～2017年31个省市的技术效率平均值，具体如表2所示。可以看出，2002～2017年31个省市农业技术效率平均水平都未达到技术有效前沿面，说明都存在一定程度的效率损失，现有农业技术的发挥程度较低，其中，农业技术效率排名前十位的省市依次为山东、江苏、河南、广东、四川、湖南、河北、安徽、广西和福建，排名后三位的都是西部地区省市，分别为宁夏、青海和西藏。

进一步从中国东部、中部、西部和东北四大区域来看，地区之间存在着农业技术效率水平的明显差距，中部地区农业技术效率平均水平为0.503，东部地区为0.472 3，东北地区为0.4，西部地区为0.268 1。易于发现，中部地区农业技术效率水平高于东部、西部、东北和平均值，而且按照由中部到东部，再由东部到东北，然后由东北到西部的顺序呈现出递减趋势。

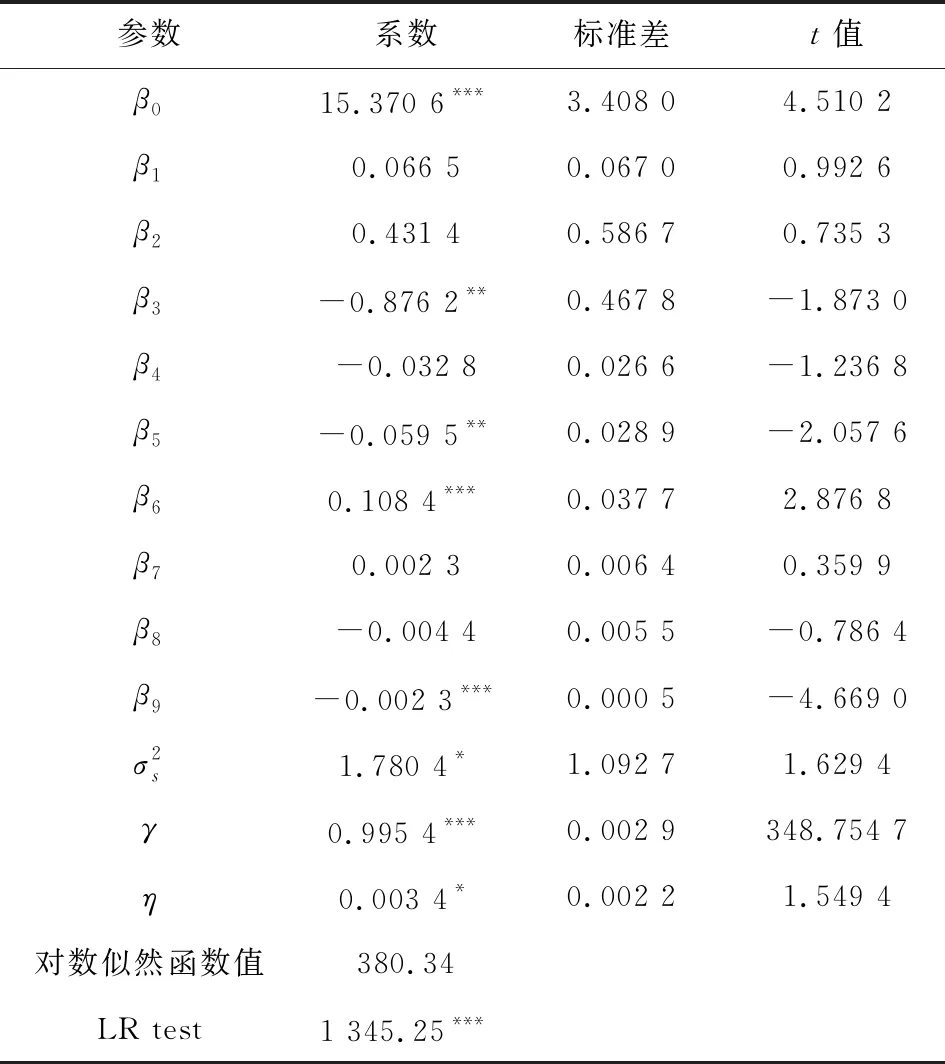
表1 前沿函数参数估计结果

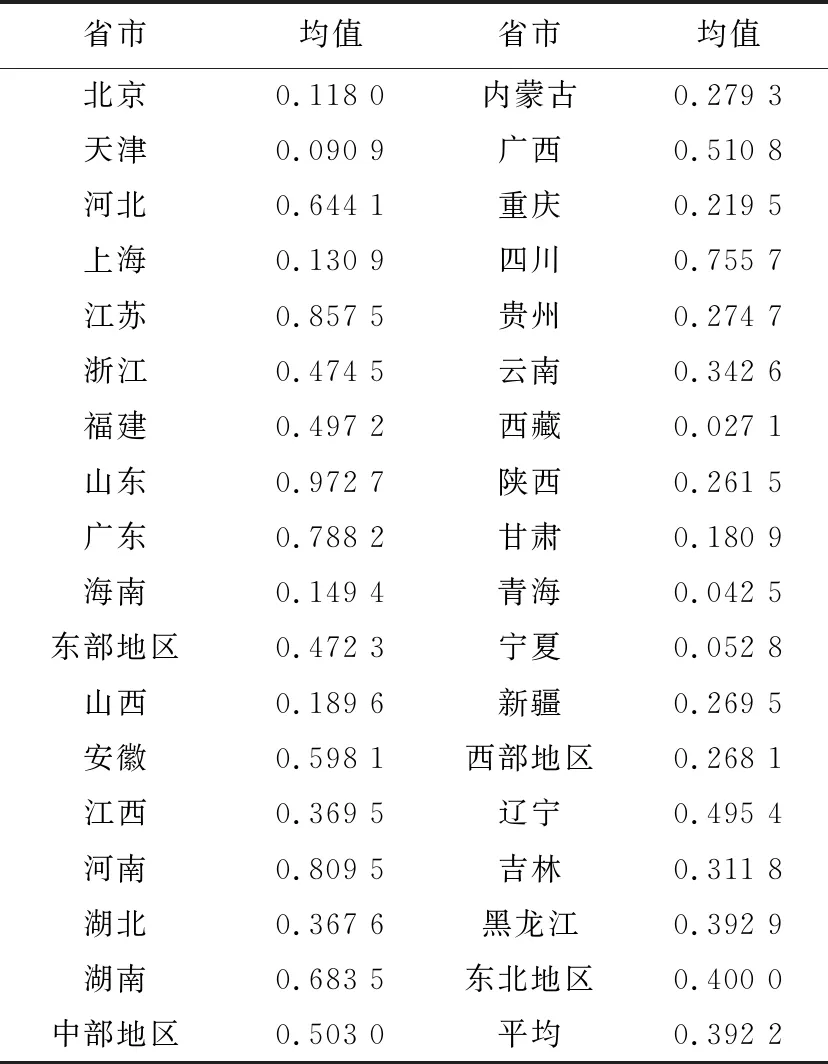
表2 2002～2017年31个省市平均技术效率水平

3.2 财政支农对农业技术效率的影响分析

3.2.1 全国整体情况分析

结合31个省市2002～2017年的农业技术效率和财政支农等面板数据，通过Eviews软件，采用Hausman检验，结果显示应构建截面个体固定效应模型，模型估计结果如表3所示。在控制其他混杂因素干扰下，依次引入财政支农的一次项(直线型)、二次项(U型)和三次项(N型)，结果表明，主要解释变量财政支农与农业技术效率之间呈现直线型的线性关系。财政支农对农业技术效率的影响系数为0.056 4，且在1%水平上显著，这表明财政支农对农业技术效率具有明显的正向促进作用。其可能的原因为：1)随着国家的一系列惠农政策的实施，比如减免农业税和增加农业补贴等，极大地提高了农民的生产积极性，促进了农业技术的推广和扩散，进而提高了农业技术效率；2)随着“一主多元”推广体系不断完善，农技推广队伍不断壮大，科技特派员制度不断推进，科研人员和广大农技人员与农民沟通更加有效，推动了农业科技成果转化、消化和吸收以及农业技术的应用，有力地提高了中国农业技术效率水平。就其他解释变量而言，城镇化水平和灌溉基础设施对中国农业技术效率具有显著的正向影响。自然灾害水平对中国农业技术效率的影响系数为负，且在1%水平上显著，表明自然环境越恶劣，越会降低农业技术效率。

3.2.2 地区差异情况分析

根据表3的结果可以看出，财政支农在总体上表现为对农业技术效率具有促进作用，但是根据图1可以看出，财政支农与农业技术效率的全样本散点图不具有明显规律性，整个图形比较分散，因此，根据国家划分的东部、中部、西部和东北地区4大经济区域，按四个地区分别进行估计，在控制其它混杂因素干扰下，并依次引入财政支农的一次项(直线型)、二次项(U型)和三次项(N型)作为模型结构形式[20]，进一步考察各区域财政支农与技术效率之间的线性和非线性作用模式，以体现地区差异性。采用Hausman检验，结果显示各区域应构建截面个体随机效应模型，模型参数估计结果如表4所示。结果发现，中部地区财政支农与技术效率之间呈现倒N型的非线性关系，东部、西部和东北地区财政支农与技术效率之间呈现直线型的线性关系。从模型的估计系数来看，东西部及东北地区财政支农的系数分别为0.039 3、0.028 2、0.137 3，且均通过了1%的显著性水平，表明财政支农对农业技术效率在东西部及东北地区具有显著正向影响，中部地区财政支农的一次项系数为-14.838 2，且在1%水平下显著，这表明在中部地区财政支农对技术效率具有显著的负向影响。

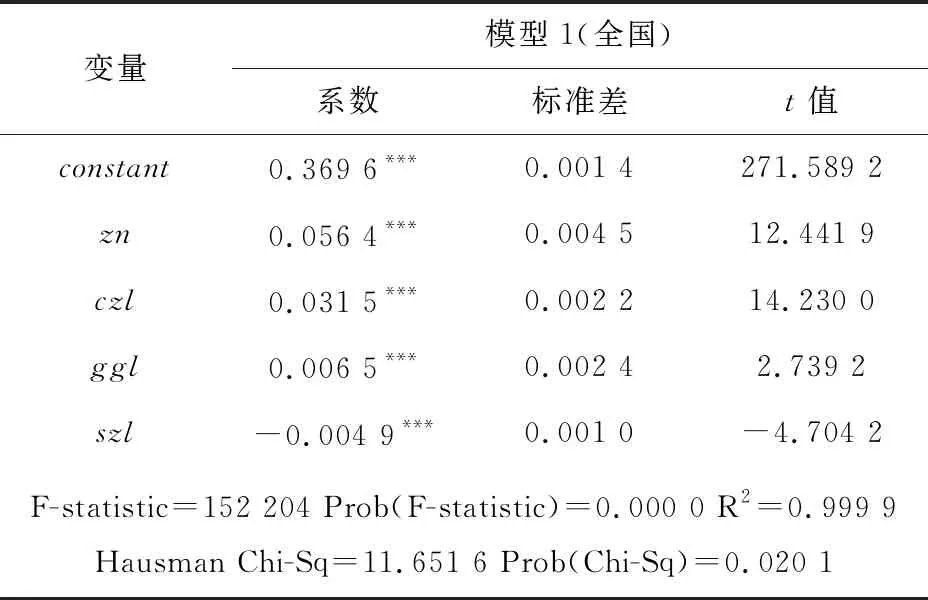
表3 财政支农与农业技术效率关系

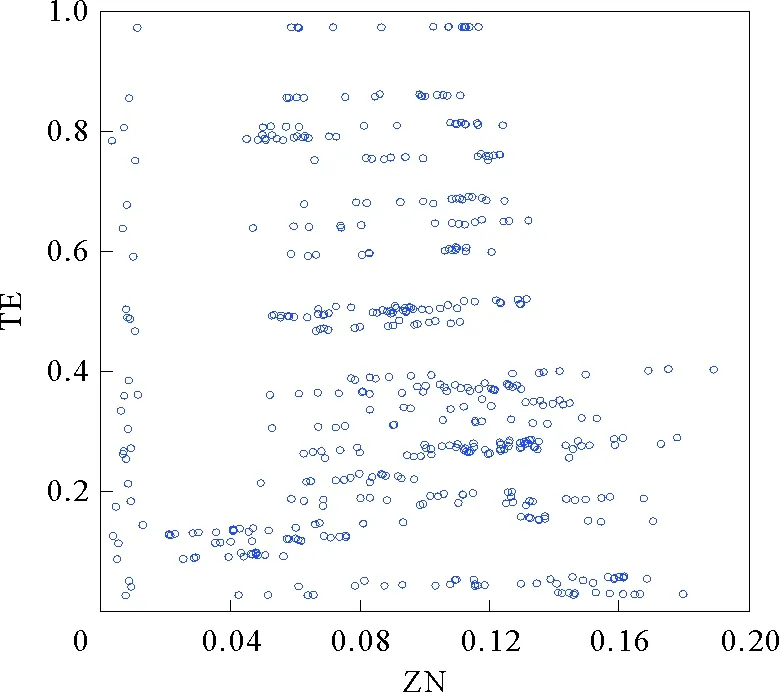
图1 财政支农与农业技术效率关系散点图

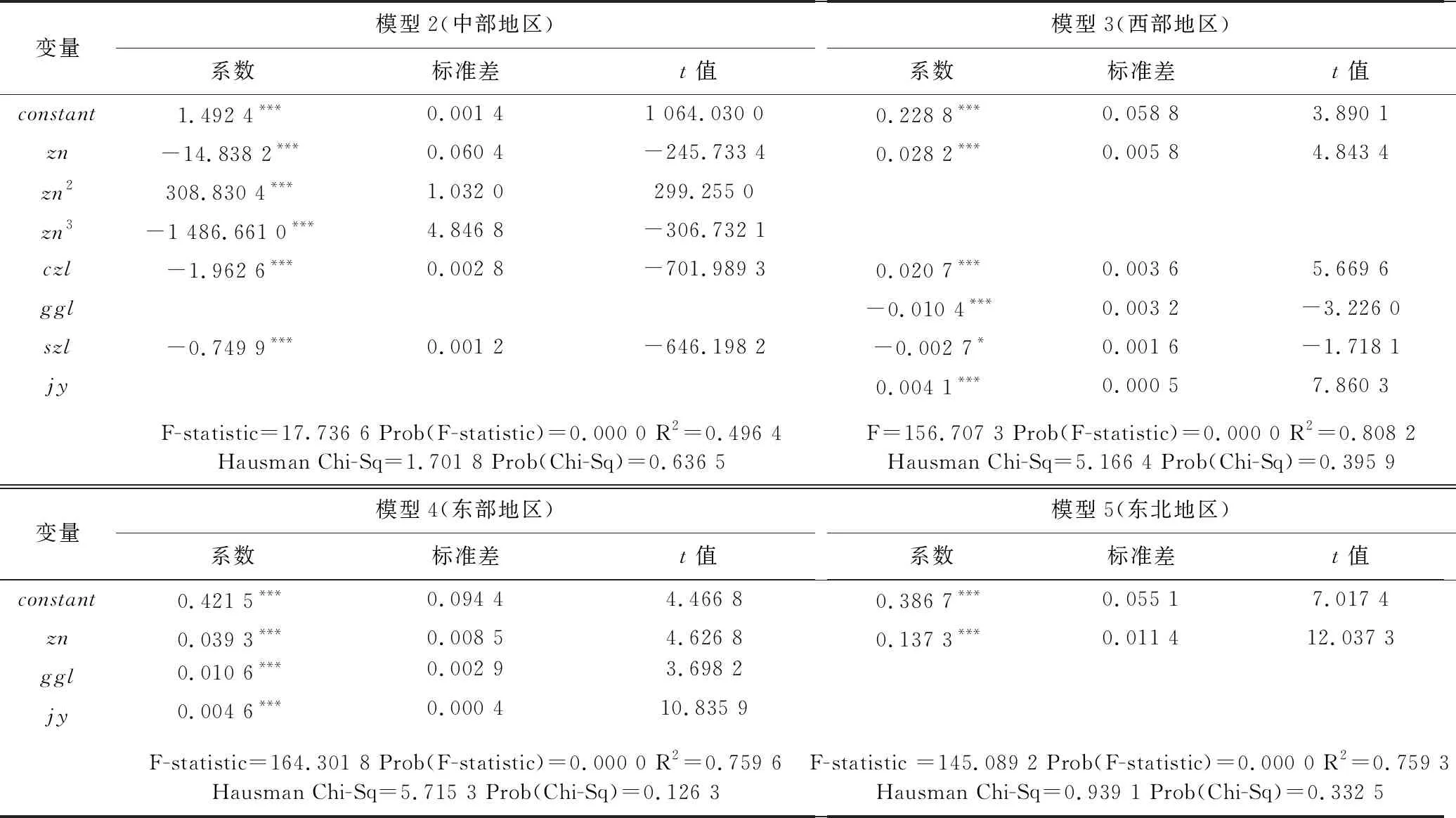
表4 各区域财政支农与农业技术效率关系

4 结论及启示

本文利用2002～2017年31个省市的面板数据，运用随机前沿超越对数生产函数测度了各省市的农业技术效率，并进一步研究了中国及四大地区财政支农与农业技术效率的关系，结果表明：1)各省市都存在农业技术效率损失，而且地区间存在明显差异，主要表现为中部地区农业技术效率平均水平高于东西部及东北地区和平均水平，呈现出中部、东部、东北、西部依次递减的趋势。2)从整体来看，财政支农支出对农业技术效率具有显著的线性促进作用；从各地区来看，中部地区财政支农对农业技术效率具有显著的倒N型非线性作用，且在考察期内体现出明显的负向影响，东西部及东北地区财政支农对农业技术效率具有显著的线性促进作用。

基于上述结论，本研究提出如下政策启示：1)进一步完善以国家农技推广机构为主导的现代农业服务体系，加快对现有农业技术的扩散和传播，推进农业新技术的广泛应用，以提高中国农业技术效率水平。通过制定合理的政策，推动先进的技术和管理经验向西部地区扩散，逐步缩小中国农业技术效率水平的地区差距。2)鉴于财政支农对农业技术效率的作用模式在各个地区存在差异性，各地区应因地制宜，结合各地实际情况，调整财政支农资金的结构及规模，加大财政支农政策效应，使得财政支农政策更好地服务农村减贫和乡村振兴战略。