动态社团发现研究综述

李永宁，吴 晔，张 伦

(北京师范大学 a.系统科学学院，北京 100875；b.计算传播学研究中心，广东 珠海 519085；c.新闻传播学院，北京 100875； d.艺术与传媒学院，北京 100875)

0 引言

社团结构是复杂网络的拓扑特性之一，发现复杂网络中的社团结构是复杂网络研究的基础性问题[1-2]。社团结构作为介于宏观网络和微观个体之间的中观结构，网络在社团层面所具有的特性是网络层面的特性所不能替代的，忽视社团结构可能会遗漏很多网络特征[3]。

随着复杂网络研究的发展，越来越多的领域借助网络分析的方式探究网络的结构与性能之间的关联[4-5]。早期的网络分析方法将网络观察数据进行叠加以发现静态社团结构，这种做法虽然可以识别社团特征，但是节点和边随时间变化的信息被忽略，无法发现网络结构的动态演化过程。近年来，随着大型社交网络的兴起和网络数据可得性的增强，动态社团发现及演化研究成为当前在线社会网络研究的热点。社团作为动态网络分析的重要基础结构，关注动态网络中社团发现问题及社团演化机制，在信息传播、影响力研究、网络群体事件等研究中都能提供新的分析视角。实际科研工作也表明，在电子商务、舆情传播、知识传播等多个领域，动态网络社团研究的可应用性不断加强[6]，动态网络的社团发现与演化等问题将成为复杂网络分析的重要关注点之一。

1 社团发现

通常认为，社团结构是指网络中的节点可以被划分为多个分组，组内节点连边相对紧密，组间节点连边相对稀疏[7]。社团发现是识别网络中节点群组关系的过程，社团发现往往能够揭示网络更深层次的特征，为理解网络的内部结构和生成机制提供了极具意义的研究视角[8]。

2002年GN算法[7]提出，引起了社团发现研究的热潮，来自生物、物理、计算机等多个学科的学者为社团发现算法提供了不同的思路，并将社团发现算法应用于各个领域。许多学者对社团发现算法进行了归纳和整理[9-11]，1)按照社团划分的出发点将算法归纳为三类，基于全局的划分[3,12]，基于节点相似性的划分[13]，和基于局部的划分[14]；2)按照社团结构的形成过程，可以分为凝聚算法[15]、分裂算法[7]、搜索算法[16]和其他算法；3)按照算法的物理背景，可以分为基于网络拓扑结构的算法[17]、基于网络动力学的算法[18]、基于Q函数优化的算法[3,19]及其它算法；4)按照社团划分结果，即划分后每个节点是否只属于一个社团，可以分为互斥的[20-21]和重叠社团发现算法[22-23]。社团发现算法可以有多种分类方式，实际研究过程中往往需要考虑网络的数据特征、形成机制和具体研究背景等问题，针对不同的网络和研究问题选择适宜的算法。

2 动态网络的社团发现算法

动态网络是一种处在变化过程中的特殊的演化复杂网络[24]，例如网络节点的加入或移除，或是节点间连边关系的改变，这些变化或许对整个网络结构的影响甚微，但是从动态演化的角度来看，随着时间的推移，细小的变化的累积可能最终会导致整个网络及其社团结构等特征的改变。近年来，随着在线社会网络的蓬勃发展，动态网络演化中的社团发现成为一个应用需求强烈且具有挑战性的研究领域[25-26]。

为了实现对动态社团的演化追踪，按照动态网络社团发现算法输入的网络数据类型，Dakiche N等人[8]将算法分为两大类：第一大类是对网络数据按照时间步进行切片，得到一组网络切片序列，将其作为输入数据然后进行社团发现及演化追踪；第二大类社团发现算法的输入数据是时态网络，时态网络是通过以边流的形式实时收集信息来实现的，对于时态网络上的动态社团检测，不需要每次都从零开始对网络进行社团发现，而是根据网络中点与边的变化，对之前已发现的社团进行更新，即，时态网络的社团发现是由一个初始的静态社团和对此社团的一系列修改(例如节点的加入和删除)组成的。但是网络切片序列和时态网络这两种数据类型是可以互相转换的，时态网络虽然在数据类型上是以“初始网络”和“每个时间点的网络变动”的形式存储，但是其数据反映的还是在每个时间点的网络结构，和网络切片序列所包含的信息是一致的，只是分析单位不同。

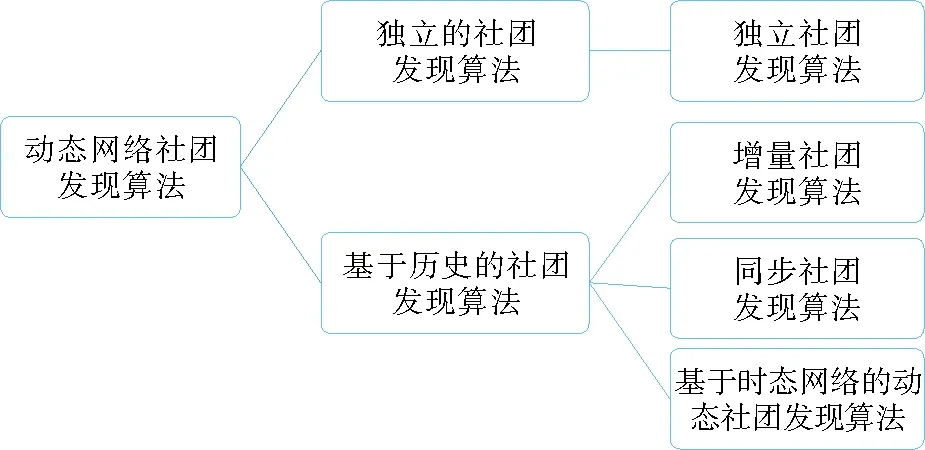
图1 动态网络社团发现算法分类图

综合来看，动态社团发现算法最本质的区别在于是否使用历史信息推断当前时刻的社团结构。例如Samie M E和Hamzeh A[27]将“网络结构的剧烈改变”作为检测网络社团的特征之一，其研究模型首先要判断各个时刻的网络切片是否发生了剧烈变化，如果是，则只使用当前切片数据进行社团发现，如果不是，则结合历史切片数据对当前切片进行社团划分。因此，本文将综合以往学者对社团发现算法的分类方式[8,28-29]，按照发现当前时刻社团时是否考察网络历史信息这一差异，对动态社团发现算法归纳为独立的社团发现算法和基于历史的社团发现算法。

2.1 独立的社团发现算法

独立社团发现算法针对的是网络切片序列数据，该类算法在对每个时间切片发现社团时，不考虑以往时间切片，对于变动较大的动态网络也可以应用。该算法分为两个阶段，第一阶段，对每一个时间步的网络切片分别进行社团发现，第二阶段，将当前时间切片的社团发现结果与上一时间切片的社团发现结果按照一定的相似性规则进行匹配，从而得出社团的演化过程。该方法将动态网络的社团发现转化为传统的静态网络社团发现问题，第一阶段可以根据不同的数据背景选择合适的算法，第二阶段可以根据社团的结构和语义等维度的相似性指标，匹配不同切片中的社团。该类方法不但可以根据实际网络在两步中选择合适的方法进行组合，而且可以处理重叠和非重叠的社团发现。例如Wang等人[30]利用节点的结构特征、点权等信息评估出社团内核心节点，然后利用社团的核心节点匹配每个独立切片网络中的社团。Sun Y等人[31]利用经典Louvain算法对每个网络切片划分社团，然后对相邻切片划分的社团两两计算相关矩阵，进而匹配和判别社团演化事件。Bródka P等人[32]采用GED(Group Evolution Discovery)方法，考虑了社团节点的质量和数量，计算出社团间的包容性，根据此指标匹配相邻网络切片的社团。该类算法的优点是思路简单、灵活，本质是在以往对静态网络社团划分后增加了网络切片的匹配问题，将动态网络的社团发现问题转化为静态网络中的社团匹配问题，能够适用于多种类型的网络。但是此类方法在匹配前后网络切片的社团时，如果相邻切片网络社团发现的结果变化较大，则匹配起来误差大、难度高[33]，并且在当前网络切片社团发现的过程中，没有考虑到历史网络的信息，每次都要重新对整个网络进行计算，计算过程存在大量的重复性，消耗计算成本较高。

2.2 基于历史的社团发现算法

基于历史的社团发现算法，包括针对网络切片序列数据的增量社团挖掘、同步社团挖掘和针对时态网络作为输入数据的社团发现算法。

增量社团挖掘算法在一定程度上兼顾了以往时刻网络切片的信息，适合处理网络结构相对比较稳定的动态网络。该类算法认为，在社团结构的动态演化中，一定时间间隔内出现剧烈改变的可能性很小，因此当前时刻的网络社团结构，一定程度上是依赖于前一时刻甚至前几个时刻中的社团结构。例如，He J和Chen D[34]将当前时刻网络切片中和上一时刻切片中连边情况相同的节点，按照一定的规则，压缩为一个新节点并替换原有节点，然后对改造后的网络切片采用Blondel算法划分社团，最后再将压缩节点还原。Shang J等人[35]借助机器学习的方法，增加了分类器来判断网络中新增节点或连边有变化的节点及其邻居节点是否需要重新划分社团，从而只通过对局部的修改便能得到当前网络切片的社团发现结果，降低了算法的时间复杂度。Zhao Z等人[36]首先检测网络初始状态下的社团结构，然后在后续时刻查找网络的增量，根据新增节点的类型(例如新增节点构成了完全独立的连通集团，或是新增节点被包含在以往某个社团内等)，决定社团结果的更新策略，同时该算法还引入了边权的时间衰退效应，以调整历史信息对当前网络社团发现的影响程度。Wang Z等人[37]提出了面向重叠社团发现的DOCET算法，同样是借助核心节点和拓扑结构，根据在时序网络切片中的增量变化更新节点社团发现结果。

同步社团发现算法是针对所有时刻的网络切片同时进行社团发现，其基本思想是通过耦合网络检测社团结构。例如通过在不同时刻网络切片中耦合相同节点之间的边，将所有的时间切片重新构建为一个新的网络，也就是将所有的时间切片之间通过加边的方式绑定为一个单独的网络，然后在此网络上进行经典的社团发现算法[38]。Aynaud T和Guillaume J L[39]通过新定义一个平均模块度来修改Louvain算法，以达到在网络切片中识别出长期存在的社团的目标。Mitra B等人[40]在引文网络数据中，按照作者文章发布时间和引用等关系，重新构建出一个合并网络，实现了对不同时刻网络关系的耦合，最后利用静态社团发现算法实现了在合并网络中识别社团结构。虽然这类算法依旧需要先采用切片的方式切割数据，并且在构建不同切片网络的关联上计算成本高于前两类算法，但是其优点是在社团发现时所有时刻的切片被同时考虑，社团划分结果的一致性得到最大程度的保留[8]。

基于时态网络的社团发现算法，不需要对网络进行切片，而是在每次网络中节点和边发生变化后，根据一定的规则，更新和调整节点的社团结果，保证了动态网络社团的连续性。Li J等人[41]通过考察时态网络中边的变化，在每一个时刻对变动边所连接的点重新评估社团，根据点的所有邻居所属于的社团情况判定该点的新社团，评估机制非常简单。Rossetti G等人[42]基于时态网络提出了Tiles算法，根据每个时刻网络中的变化，对网络使用标签传播的思想重新评估变化相关的节点及其邻居节点的社团关系。Nguyen N P等人[43]针对时态网络中的重叠社团发现问题提出了AFOCS算法，该算法在初始时会识别网络中内部密度大于一定程度的小社团，并将高度重合的紧密社团合并，在此基础之上再根据时态网络的实时变化更新节点的社团结果。Boudebza S等人[44]基于派系过滤和标签传播的方法提出了OLCPM算法，先发现网络中的核心社团，再通过标签传播标注外围节点，该算法在处理网络中的变化时，会根据是节点还是边的变化，按照不同的规则更新社团结果。该类算法虽然能很好地保持社团发现的连贯性，但是时态网络要面临的网络变动量是巨大的，所以基于时态网络的社团发现算法很难在每一步更新时使用较为复杂的算法。除此之外，由于每一步的社团结果都是建立在前一步的结果之上，该类算法不能保证最终得到的社团发现结果是全局角度的最佳结果[44]。

整体而言，基于历史的社团发现算法更适用于结构相对稳定的动态网络，能够较好地利用前一时刻甚至前几个时刻网络切片中的历史信息，保持社团的连贯性。该类算法虽然比独立的社团发现算法在社团划分这一步更复杂，但是该类算法将前一时刻的结果作为输入数据来识别当前时刻的社团，避免了不同时刻网络切片间的社团匹配的问题；与此同时，在大规模网络中，该类算法能够有效降低计算成本，更适合当前大数据环境下的在线社会网络的研究。

社团发现结果的稳定性和可靠性会影响后续对于动态社团演化事件的判定和预测，因此，在社团发现阶段，应该尽可能保证结果的稳定性和可靠性。需要注意的是，在动态网络的社团发现算法中，如果使用切片数据，在将网络按照时间窗口切分时，切片策略会直接影响到后期社团发现和演化的研究结果。时间窗口切分方式可以分为按照等时间长度切分，按照每个时间窗口具有等量的关系数切分，以及根据数据的具体背景按照任意长度切分。Saganowski等人[45]指出网络切片可以分为互斥的、重叠的和累积的，在切分网络过程中，应该注意：1)对于变化较快较大的网络，建议采用重叠的时间窗口，通常采用30%的偏移量以保证能获取到足够的时间窗之间的连续事件(例如连边变化)；2)窗口大小应该和实际数据的背景相结合；3)如果研究的对象是持续存在的社团，建议采用累积的时间窗口，尽量保存网络的持续性和增长性的事件；4)在处理相对稠密并且节点间的关系会反复出现的网络时，可以尝试使用互斥的时间窗口来降低计算量；5)在设计时间窗口的类型和大小时，可以通过多次尝试以达到最佳的切分结果。

网络的切分、数据的处理和社团发现的算法都可以有多种选择，因此，需要有合适的社团发现效果评价指标，才能选择出最合适的算法。在社团发现算法的评估方面，无论是静态网络还是动态网络，都是主要以模块度和NMI为评价指标。模块度考察的是社团结构的强度，通过比较网络中各社团的边密度和随机网络中对应子图边密度之间的差异来度量社团结构的显著性，而NMI是通过社团发现结果和真实社团结构之间的相似性。同时，常用的基准图包括空手道俱乐部网络[46]、海豚间关系网络[47]、美国大学生足球俱乐部网络[7]、政治书籍网络[48]，和大学电子邮件网络[49]等。这些经典的公开数据集虽然具有很好的质量，但是由于其数据年份较早，和当前的众多实际在线网络数据相比，在数据量级和网络性质方面还是有一定差异。由于真实网络的社团结构数据往往难以获取，相比之下，模块度作为评估社团的指标应用范围更广，但是模块度的计算复杂度较高[50]，因此也有学者提出对模块度算法的优化，或针对不同的网络类型[51]，或通过降低算法的时间复杂度以适用于大规模网络[28,52]，或解决模块度优化中存在的分辨率问题[53]。

3 动态社团演化事件

社团的动态发展是网络科学尤其是社交网络分析的一个重要领域，关注的是特定群体如何随时间变化[54]。Palla G等人[55]将网络演化事件总结为生长、萎缩、合并、分裂、出生和死亡。这一归纳被许多学者沿用[8,35,56]，也有学者对此模型进行了进一步的补充，例如Cazabet R和Rossetti G[57]提出了社团的复活，Tajeuna E G等[58]都使用了社团的持续这一概念；Mohammadmosaferi K K和Naderi H[59]将社团演化过程进一步细化，新增了合并且增长、部分合并、部分合并且增长、分裂且增长，和部分存活且生长。

表1 社团演化事件归纳

续表1

实际上，社团演化事件通常只是为了描述网络切片中社团的一些发展状态，并不适合用来描述精细时间粒度下的网络复杂动态[57]。在具体的判定过程中，阈值的设定会严重影响演化结果的判定，例如很多算法通过计算相邻网络切片中各个社团间的相似性，给定恰当的阈值决定两个社团是否匹配，假若t时刻的两个社团各自流失了小部分节点，这些节点在t+1时刻组成了新社团，如果判定社团匹配的相似性阈值设置较高，则新社团会被判定为出生，反之将被视为由前一时刻两个社团部分合并而来。

4 动态社团演化研究

探究网络的社团结构及其演化过程，有助于认识和发现实际网络中事物的关联和发展规律。例如Wang R和Rho S[60]认为，合作行为建立了个体之间的关联网络，个体与所在社团内外其他个体的合作行为，推动了社团和网络结构的动态演化。Varga A[61]建立了1950年到2018年Web of Science中SCI期刊引文网络，发现学科之间的距离越来越短，学科之间的交叉现象更加明显。Singh C K和Jolad S[62]通过建立印度物理学家1970～2013年间的合作网络，追踪合作社团的规模变动，探究了印度物理学家与外国物理学家在不同期刊上的合作关系，并找出了每个时期最有影响力的作者。Atzmueller M等人[63]研究了面对面接触网络中群体形成和演化，描述了在一个会议过程中，个体交流群组的演化，并发现群组规模的分布在茶歇，会议和空闲时间差异明显。齐金山等人[64]在新浪微博网络测量Gnutella等数据集上实验发现，社会网络中节点的出现和消失频繁程度会影响社团稳定性以及社团结构的演化。社团结构的演化作为动态网络中的重要特性，对于网络的生存发展和网络中信息的传播等都具有重要的研究价值，但是目前关于动态社团的研究中，更多集中于如何提出更有效的动态社团发现算法，对社团演化问题关注还不足够[37]，实际上，无论是引文网络，还是社交网络，随着数据可得性的提高，对网络性质和特征的探究还可以被进一步挖掘。

5 动态社团研究未来方向

首先，随着大规模的复杂网络越来越多，尤其是多内容和动态变化的大型社交网络的迅速增长[60]，如何降低动态网络社团发现算法的复杂度是一个不可避免的难题。动态网络社团发现算法的复杂度，与网络的节点数量以及网络变化的数量紧密相关[57]。社团发现算法应适用于大型动态网络，甚至是采用分布式的计算方式[10]，以适应现实生活中大规模、多变动、持续久的复杂网络。与此同时，在用户生产内容为主的网络环境中，如何去除繁杂网络中的噪声数据，乃至在社交网络的研究中如何处理社交机器人等因素的影响，都是值得考虑的问题。

其次，在对动态网络进行社团发现时，应注重结合网络的现实场景，不局限于网络的拓扑特征，从而提高社团划分的准确度和稳定性。社会网络的实体并非总是单一类型，实体间的关系往往也是多样的[68]，当面对社团核心节点不明显的、动态变化剧烈的网络时[69]，社团发现的难度大大增加。因此，在社团发现时要充分挖掘网络结构特征，例如结合网络中的高阶连接模式[70]，发现社团结构和模体结构之间的关联和特征。实体在网络中呈现的属性可能是多刻面的、高维的、稀疏的，如何将语义信息、关系信息、交互信息等多元信息有效综合进行结构推断和预测将成为未来的一个重要研究领域[71]。

再次，尽管目前已有多个经典的网络社团发现算法检测的基准图，但是包含真实社团结构的动态网络数据还是相对稀缺的[50,72]。在目前大数据的信息环境之下，如何能够推动真实社团结构的数据库的建立和共享，如何能够通过多源数据实现网络数据中的实体关系推断以丰富基准图数据库，这些问题都需要通过多方协作、共同解决。

最后，在研究过程中应拓宽动态社团发现与演化研究的应用场景，将复杂网络的研究思想与其它学科相结合。随着互联网的发展，社交网络成为了社会科学、政治经济、文化传播等多个领域的研究对象，充分利用信息资源和跨学科的计算方法，能够将动态社团的研究方法与其它社会系统相结合，为各领域提供新的研究视角和技术支持，尤其是社团演化研究对预测实际社会网络的生命周期等方面的应用还有很大的发展空间。