卷积神经网络复杂性质与准确率的关系研究
2021-05-11王光波孙仁诚邵峰晶
王光波,孙仁诚,隋 毅,邵峰晶
(青岛大学计算机科学技术学院,山东 青岛 266071)
0 引言
近年来,以深度学习为主导的人工神经网络模型结构日趋复杂,网络的层次不断加深、链接关系更加繁杂。如何设计有效的人工神经网络以提升深度学习的效果尚无有效的指导方法。已有研究表明神经网络的拓扑结构会对神经网络的性能产生较大的影响。Simard[1]验证了小世界神经网络比规则网络和随机网络具有更快的收敛速度。在2019年Saining Xie[2]分别对ER,BA,以及WS三种模型生成的随机连边神经网络进行了探索,在计算域相同的情况下WS(4,0.75)生成的随机网络在ImageNet上具有最高的准确率。因此,应用复杂网络的“小世界”、“无标度”等复杂网络性质来指导深度学习网络结构设计或许为深度学习模型设计提供理论依据。然而可以体现网络结构的复杂网络性质有很多,其中包括平均度,网络直径,图密度,模块化,平均聚集系数,平均路径长度等。平均聚集系数可以体现网络中节点聚集成团的程度,网络直径可以体现网络中任意两个节点的最大距离。具体哪些性质所体现的网络结构与神经网络的准确率有关尚不能明确。
因此,本文首先分析了先进的卷积神经网络的复杂性质,之后设计出了多组拓扑结构不同的卷积神经网络,通过在标准数据集的训练和公式计算获得了它们的准确率和拓扑复杂性质数据。通过相关数据探究了神经网络性能和拓扑结构复杂性质的关系。这为进一步设计出更好的卷积神经网络提供了指导。
1 复杂网络与卷积神经网络
1.1 复杂网络与卷积神经网络的定义
复杂网络是对复杂系统的抽象和描述方式,任何包含大量组成单元(或子系统)的复杂系统,当把构成单元抽象成节点、单元之间的相互关系抽象为边时,都可以当作复杂网络来研究。
前馈神经网络(Feedforward Neural Network,FNN)[3],简称前馈网络,是人工神经网络的一种。前馈神经网络采用一种单向多层结构。其中每一层包含若干个神经元。在此种神经网络中,各神经元可以接收前一层神经元的信号,并产生输出到下一层。第0层叫输入层,最后一层叫输出层,其他中间层叫做隐含层(或隐藏层、隐层)。隐层可以是一层。也可以是多层。整个网络中无反馈,信号从输入层向输出层单向传播,可用一个有向无环图表示。
卷积神经网络(Convolutional Neural Networks,CNN)是一类包含卷积计算且具有深度结构的前馈神经网络。
1.2 复杂网络与卷积神经网络的转换
如图1所示,图中卷积神经网络的灰色节点由大量的卷积层、池化层等操作函数组成,这些操作函数便是卷积神经网络这一系统的组成单元。在卷积神经网络中,每一个操作函数会将特征图进行处理,处理完成后将特征图传递给下一个操作函数。由此可得,操作函数之间具有传递信息的关系。结合复杂网络的定义可得一组对特征图进行操作的函数就可以抽象为复杂网络中的一个节点。特征图在函数之间的传递便可以抽象为节点之间的连边。卷积神经网络可以转换为复杂网络。
卷积神经网络的拓扑结构会影响网络的性能。要探究网络性能与对应复杂网络性质的关系,就需要借助复杂网络,对实际卷积神经网络的拓扑结构进行分析,在此基础上对网络性能与对应复杂网络性质的关系进行探究。
1.3 卷积神经网络网络性质的分析及问题
卷积神经网络的网络结构由最初从左到右的链式结构LeNet[3],AlexNet[4],VGGNet[5]等,发展到了如今的含有跨层连边的多样化布线结构Inception-v4[6],ResNet[7],DenseNet[8],NASNet[9]等。参数数量越来越多,准确率越来越强大。
最初的卷积神经网络都是链式结构的,网络的卷积核会对特征图进行卷积操作。特征图在网络内部的流动使得神经网络可以看作一种有向的复杂网络。如图2所示6层的卷积神经网络,因为卷积神经网络的权重共享,网络的对应复杂网络可以看成是一种规则网络。
如图3从左到右是3种先进卷积神经网络的一部分,以及k=4的最近邻耦合网络。ResNet的每一个节点都会与后面一个相邻节点有一条连边,对于后面的第三个节点也会有一条连边,可以称这样的连边为跨层连边。所以ResNet的对应复杂网络是一个规则网络。NASNet的每一个节点都会与后面一个相邻节点有一条连边,对于后面的第二个节点也有一条连边。在较大的粒度来看NASNet的对应复杂网络是一个k=4的有向最近邻耦合网络。DenseNet中的每一个节点都会与这个节点后面的每一个节点有一条连边,这种网络也是一种规则网络。
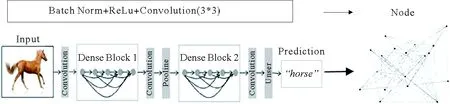
图1 复杂网络与卷积神经网络的转换
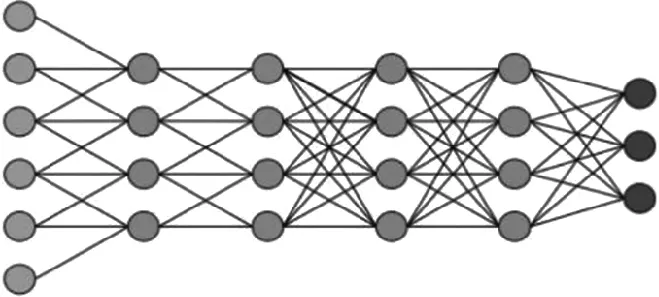
图2 6层的卷积神经网络
通过分析发现,如今卷积神经网络的对应复杂网络都是规则网络,规则网络会有较大的聚集系数和较大的平均路径长度。卷积神经网络的准确率与对应复杂网络的较大的聚集系数和较大的平均路径长度的关系需要进一步通过实验验证。
2 卷积神经网络拓扑性质的研究
2.1 问题描述
经过上述分析,需要进一步验证卷积神经网络准确率与网络聚集系数和平均路径长度的关系。网络的复杂性质有很多,除了聚集系数[10]和平均路径长度[11],平均度、网络直径、图密度、模块化[12]等也可以在一定程度上反应卷积神经网络拓扑结构的一些特性。
希望通过实际模型探究卷积神经网络的准确率与复杂性质的关系。这就要求设计出多组拓扑结构不同的卷积神经网络。为了更好地设计拓扑结构和描述问题,给出如下定义:
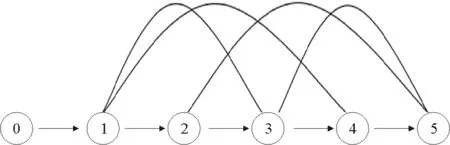
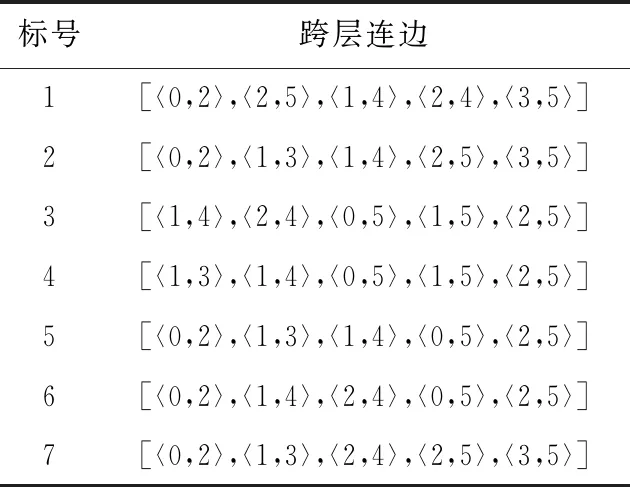
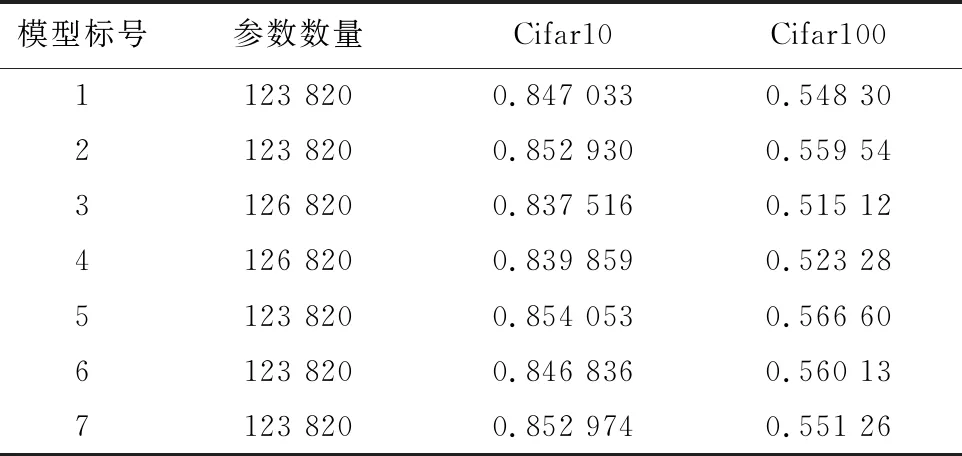
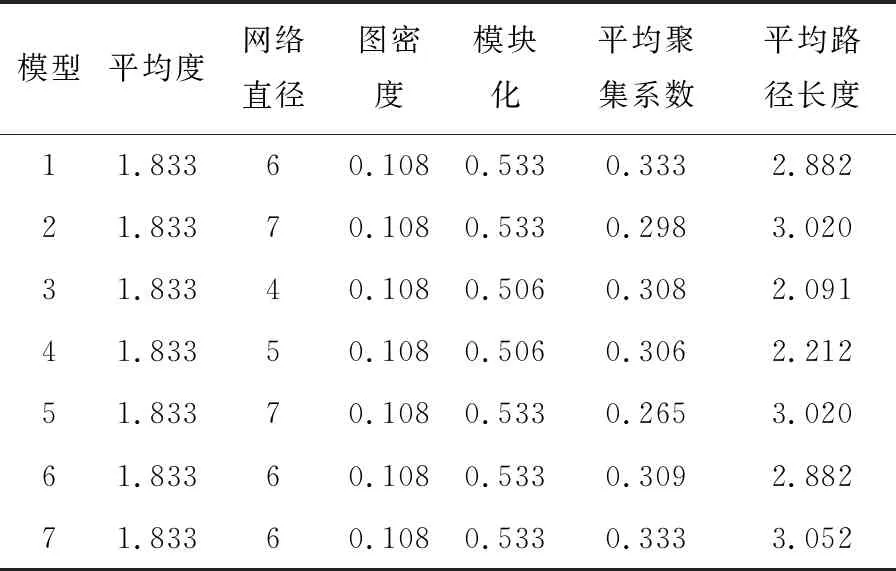
定义1基线网络模型记为Bnet(Vb,Eb),其中,Vb={vi|vi为节点,0 定义2交叉网络模型为在基线网络的基础上,添加m条跨层连边得到,记为Cnet(Vc,Ec),其中,Vc=Vb,Ec=Eb∪El,这里El={〈vsj,vwj〉j|vsj,vwj∈Vb,0≤sj 图3 卷积神经网络和最近邻耦合网络 图4 交叉网络 图4给出了交叉网络的示意图,交叉网络有两种连边。第一种连边是相邻节点之间的连边,用Eb表示,第二种连边是跨层连边,用El表示。根据定义2,可以通过人工设计不同的跨层连边,将跨层连边添加到基线网络中得到不同拓扑结构的交叉网络。 得到不同拓扑结构的交叉网络之后,需要进一步将只有节点和连边的网络扩展为完整的卷积神经网络。这需要给出卷积神经网络的相关定义,然后在定义的基础上,通过算法建立完整并有较高性能表现的卷积神经网络,命名为交叉卷积神经网络。因为交叉网络的拓扑结构是多样性的,所以对应得到的卷积神经网络的拓扑结构也是多样性的。在正式进行实验之前,需要进行一下卷积神经网络的拓扑复杂性分析,之后通过交叉卷积神经网络这一实际模型探究卷积神经网络准确率与网络复杂性质之间理论上存在的关系,最后通过实验进一步验证这一关系。 影响卷积神经网络准确率的因素有很多,实验中需要注意控制单一变量。以交叉网络为基础,在节点数量和连边数量一定的条件下,人工设计出不同拓扑结构的交叉网络。然后将不同拓扑结构的交叉网络转换成对应的卷积神经网络。为了将网络转换成卷积神经网络,这里给出卷积神经网络的相关定义。 考虑图像X0在卷积神经网络中前向传递,卷积神经网络包括L层卷积层,每一层都是复合卷积层Hi(x)或Ti(x),i表示第i层。Hi(x),Ti(x)是一种由批量归一化(BN)[13],激活函数(ReLU)[14],池化或卷积(Conv)组成的连续操作。BN函数可以加速网络收敛,ReLU是一种激活函数操作,Conv是卷积操作,Pooling是池化操作,可以减小特征图尺寸。 定义3复合卷积层指对特征图x依次进行批归一化、ReLu激活及卷积窗口为r×t的卷积运算过程,记为H(x)=Conv(ReLU(BN(x)),r,t)。 定义4传输层,指对特征图x依次进行批归一化、ReLu激活及池化运算过程,记为Transition layerT(x)=Pooling(ReLU(BN(x)))。 定义5复合函数层,传输层或复合卷积层统称为复合函数层。 定义6特征图链接指复合函数层将新产生的特征图传递到下一个复合函数层的过程。这一过程会将前面传递过来的特征图与已有特征图进行拼接,形成一个较大的特征图。记为cat(x0,x1)=[x0,x1],x1是源复合函数层传递过来的特征图,x0是已有特征图。 定义7交叉卷积神经网络是将b个交叉网络串行连接得到的网络,在交叉网络的基础上通过应用算法1可以得到。它的拓扑结构与交叉网络大致相同。 算法1交叉卷积神经网络生成算法: Input:(Cnet(Vc,Ec)),b,r,t Output: (Cross convolutional neural network(Vc,Ec)) Initialise Composite function setH(x)=Conv(ReLU(BN(x)),r,t)T(x)=Pooling(ReLU(BN(x))) foreachvinVcdo: If v is last node: replacevwithT(x) Else : replacevwithH(x) foreinEcdo: replace e withcat(x0,x1) {x0,x1is the feature map produced byT(x) orH(x)} Cross convolutional neural network(Vc,Ec){Initialize the Cross convolutional neural network} fori=0;i vi=Cnet(Vc,Ec);vi+1=Cnet(Vc,Ec) 〈vi,vi+1〉=cat(x0,x1) {x1is produced byvi,x0is produced by other node} Vc=Vc∪vi∪vi+1;Ec=Ec∪〈vi,vi+1〉 result= Cross convolutional neural network(Vc,Ec)-T(x)+Classification layer {Replace the final Transition layer with the classification layer} Output= result 交叉卷积神经网络的拓扑结构不同,复杂性质也会不同。特征图在不同拓扑结构的交叉卷积神经网络中流动时会产生不同的结果,所以,交叉卷积神经网络的复杂性质在一定程度上会对交叉卷积神经网络的准确率造成影响。 网络的复杂性质包括:平均度,网络直径,模块化,平均聚集系数,平均路径长度等。这里通过平均路径长度和平均聚集系数[12]分析网络的复杂性质如何对网络的准确率造成影响。 复杂网络中的平均路径长度是任意两个节点之间距离的平均值。根据交叉卷积神经网络生成算法可知两个节点之间的距离在卷积神经网络中便是特征图从一个网络层到另一个网络层经过的H(X)或T(X)次数。网络的平均路径长度可以在一定程度反映出交叉卷积神经网络特征图的卷积细化程度。 根据复杂网络的相关理论,交叉卷积神经网络的拓扑结构中如果一个节点i的度为ki,那么节点i的聚集系数[10]Ci定义为 (1) 在拓扑结构上ejk表示节点j有一条指向节点k的连边。Ni表示节点i的邻居节点的集合。式(1)中的分子是节点i的ki个邻居节点之间实际存在的边数。分母是点i的ki个邻居节点之间至多存在的边数。分子和分母的比值便可以反映节点聚集成团的程度。根据式(1)描述,在ki一定的情况下,ki个邻居节点之间实际存在的边数,就会直接影响节点i聚集系数的值。 在交叉卷积神经网络中,这ki个节点对应的卷积层都接收到了卷积层i产生的特征图,这ki个卷积层之间如果互相传递的特征图较多,聚集系数就会较大,如果传递的特征图较少,聚集系数就会较小。因此,网络的平均聚集系数可以反映网络中各个卷积层特征图聚集成团的程度。 经过以上分析,交叉卷积神经网络的复杂性质可以反映交叉卷积神经网络每一个卷积层或传输层产生的特征图之间的传递与融合的某些特性,从而在一定程度反应交叉卷积神经网络的准确率。接下来通过实验进一步验证交叉卷积神经网络复杂性质与交叉卷积神经网络准确率的关系。 为了验证交叉卷积神经网络复杂性质与网络准确率的关系,需要设计多组复杂性质不同的模型。为了实现这一目标,首先通过定义1和定义2人工设计出模型的拓扑结构。之后通过应用算法1,生成多组拓扑结构不同的卷积神经网络。具体实施方案如下: 根据定义1,设参数n=6,初始化基线网络,网络中有标号为0-5的6个节点。人工预设7组拓扑结构不同的跨层连边,如表1所示。为了进行对照实验,标号(1,2),(3,4),(5,6,7)是3组对照实验,它们的连边既有相同又有不同,使得它们的复杂性质一定不同。 设参数m=5,在基线网络的基础上,根据定义2将表1中每一组跨层连边添加到基线网络中,得到7组拓扑结构不同的交叉网络。为了使拓扑结构具有多样性,将其中2组交叉网络的拓扑进行修改。去掉了连边〈4,5〉,增加了连边〈0,2〉。最终结果如表2所示。 表1 人工预设的7组跨层连边 表2 不同拓扑结构的7组网络 最后将设计出的拓扑结构转换为完整可训练的卷积神经网络。设定参数r=3,t=3,b=3通过应用算法1,由表2中这7组交叉网络生成对应的交叉卷积神经网络。根据算法1可知交叉卷积神经网络的拓扑结构与对应交叉网络的拓扑结构相同。因为通过m,n控制了节点数量和连边数量,所以生成的7组模型的参数数量基本相同。 通过训练7组交叉卷积神经网络和计算它们的复杂性质获得实验数据。 训练交叉卷积神经网络,数据集分别使用了Cifar10和Cifar100。训练的超参数设置如下:学习率lr=0.001,设置学习率每隔80个训练轮次衰减为原来的10%,batch_size=64,优化器使用Adam[15],每个模型训练300个轮次,为了降低随机性,取后200个轮次准确率的平均值作为模型的评价。收集了这两个数据集上的准确率表现和网络参数数量后制作成了表3。 交叉卷积神经网络的拓扑结构与交叉网络的拓扑结构相同,根据网络复杂性质的相关公式,直接计算交叉网络的平均度,网络直径,图密度,模块化,平均聚集系数,平均路径长度,得到了交叉卷积神经网络的复杂性质,将结果进行汇总制作成了表4。 通过对比表3和表4的数据后发现,表4中的7个复杂网络的性质只有平均聚集系数会和卷积神经网络的准确率有一定的关系。具体表现为在参数量相同的情况下,聚集系数小的网络,卷积神经网络准确率会高。模型3,4参数数量相同,模型4的平均聚集系数比模型3稍微小一些,模型4的卷积神经网络准确率表现比模型3也高一些。模型1,2,5,6,7的参数数量相同,模型5有最高卷积神经网络准确率的同时平均聚集系数也是最小的。 表3 7组模型的参数数量以及在Cifar10和Cifar100上的准确率表现 表4 7组模型的复杂性质 经实验数据可得到结论:在统计意义和参数数量一定的情况下,卷积神经网络对应复杂网络的平均聚集系数越小,卷积神经网络的准确率越高。这就要求在设计新的卷积神经网络时,在网络拓扑结构上减少节点聚集成团的特性,降低平均聚集系数的值。 本文通过理论分析和对照实验,利用设计出的拓扑结构不同的卷积神经网络进行准确率和复杂性质的对比。得到了网络拓扑的聚集系数会影响卷积神经网络准确率的结论。具体表现为在统计意义上,聚集系数越小,卷积神经网络的准确率越高。这为卷积神经网络拓扑结构的设计进一步提供了理论依据。在今后的研究中,需要进一步探究聚集系数与卷积神经网络的准确率相关性。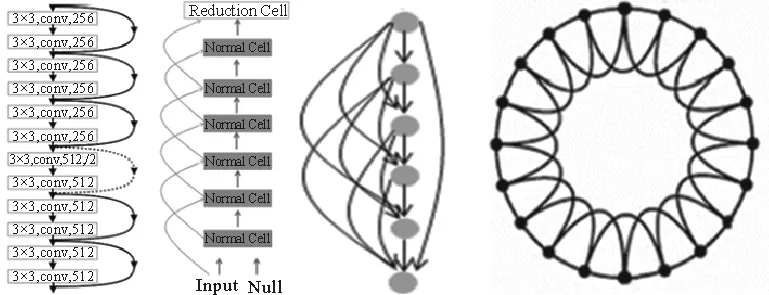
2.2 复杂网络拓扑到卷积神经网络的生成算法
2.3 卷积神经网络拓扑复杂性分析
3 实验过程与分析
3.1 实验设计

3.2 实验数据
3.3 结果分析
4 结论
