求解一类无关并行机调度的遗传迭代贪心算法

曾创锋，刘建军，陈庆新，毛 宁

(广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006)

家电企业总装车间中，来自客户的工单具有多品种、小批量的特征，每一张工单都将生产某一型号的一款产品，生产该型产品需要指定的型号物料；加工单元由多条异构的并行加工线体构成，加工线体所采用的技术、线体新旧程度有所不同，部分型号的物料只能在指定的部分线体上进行加工，同时，根据相邻工单所加工的产品型号及其使用的物料型号的异同，需要对线体的设置进行相关调整。这类问题属于典型的带工单加工约束和序相关设置时间的无关并行机调度问题(unrelated parallel machine scheduling problem with job processing constraints and sequence-dependent setup times，UPMSP_JPCSST)，即同一张工单在不同线体上的加工时间不尽相同，且工单只能在特定的部分线体上进行加工，同时，工单上机的设置时间取决于前后相邻工单的顺序。该问题以极小化最大完工时间(Cmax)为优化目标，使用三元组[1-2]可以将其描述为Rm|si,j,Mj|Cmax。UPMSP_JPCSST是UPMSP中非常复杂的一类，属于NP完全问题，对其进行求解非常困难。因此，对UPMSP_JPCSST求解算法的研究具有较高的理论和应用价值。

目前对于UPMSP_JPCSST的求解方法主要有精确算法、启发式规则和元启发式方法。其中，精确算法经常使用混合整数规划(mixed integer programming, MIP)模型、分枝定界[3]等方法以求得问题的最优解，但求解费时并受限于问题的规模，难以对问题进行快速求解；而启发式规则[4]虽然易于实施，但所得解的质量难以保证；而元启发式方法则有较大的塑性空间，其求解速度与求解质量取决于对算法本身的挖掘，一个优异的元启发式方法能在合理的时间内得到尽可能好的满意解[5]，因此得到越来越多的关注[3,6-8]，如遗传算法(genetic algorithm, GA)、模拟退火算法(simulated annealing, SA)、禁忌搜索算法(tabu search, TS)等。作为一种广泛应用于求解车间调度问题的方法，GA算法通过选择和交叉操作从父代种群获取优良的遗传信息，进而对问题的解空间中可能存在优良解的区域进行搜索，这使得GA具有全局搜索能力，但正是过于注重搜索的广度反而导致挖掘深度不足。而将具有概率突跳机制的SA、具有记忆禁忌机制的TS等注重局部信息深度挖掘的搜索算法与GA算法相结合，能弥补GA算法局部优化能力的不足，且能帮助其跳出或避免陷入局部最优，增强搜索性能。因此，相关改进型混合算法[9-12]，如GASA、GATS等得到广泛的重视。但是该类算法自身框架复杂性可能会导致其单代运行时间较长，使得这类算法具有运行时间依赖性，仍难以对问题进行快速求解。

迭代贪心算法(iterated greedy algorithm, IG)[13]是一种新颖的、基于单解的、包含破坏与构建2个阶段的启发式算法。IG涉及极少控制参数，计算速度极快，优化效果优异，得到广泛重视，并应用到UPMSP中[14]。算法的破坏、构建操作可能会因为其机制及其邻域的契合性、算法的快速性而适合UPMSP_JPCSST IG中序相关设置时间角度的优化。因此，将传统GA与计算速度快、侧重从局部层面对解空间进行搜索的IG算法进行合理融合，具有较高的研究价值。根据文献调研，对于UPMSP，基于GA和IG的混合求解算法的研究尚无文献报道。

本文提出一种遗传−迭代贪心算法(genetic algorithm-iterated greedy algorithm, GAIG)，用以求解最小化最大完工时间Cmax指标下的UPMSP_JPCSST。

1 研究问题及数学模型

1.1 问题描述

设工单集合J有n个相互独立的工单，这些工单在时间为0时可用；m台加工线体(m＞1)构成一个制造系统；工单j (j∈J)需加工数量不等的某一款产品，该款产品只需1道工序即可完工，且只能由满足工单加工约束的线体加工；工单的加工时间取决于加工线体及该工单需加工产品的数量，任何线体k同一时刻只能加工1个工单；在线体上加工不同产品时需要设置时间，设置时间依赖于相邻工单所加工产品的产品类型和物料类型属性。

1.2 假设条件

1) 工单数量及其对应需生产的产品数量已知且确定；

2) 每个工单只生产一款产品，且不能被分割；

3) 每个工单将加工的产品型号及其物料型号已知且确定；

4) 各种物料型号的线体适用集合已知且确定；

5) 对于每一种物料型号，至少存在一条线体可以完成加工；

6) 工单一旦在线体上开始加工，就不允许中途停止而加工其他工单；

7) 同一条线体同一时刻只能加工一张工单；

8) 所有的工单和线体在0时刻可用。

1.3 符号定义

模型相关变量如表1所示。

表1 模型参数符号及其说明Table 1 Model parameter symbols and descriptions

1.4 数学模型

根据以上假设与条件，对Rm|si,j,Mj|Cmax建立的数学模型如下。

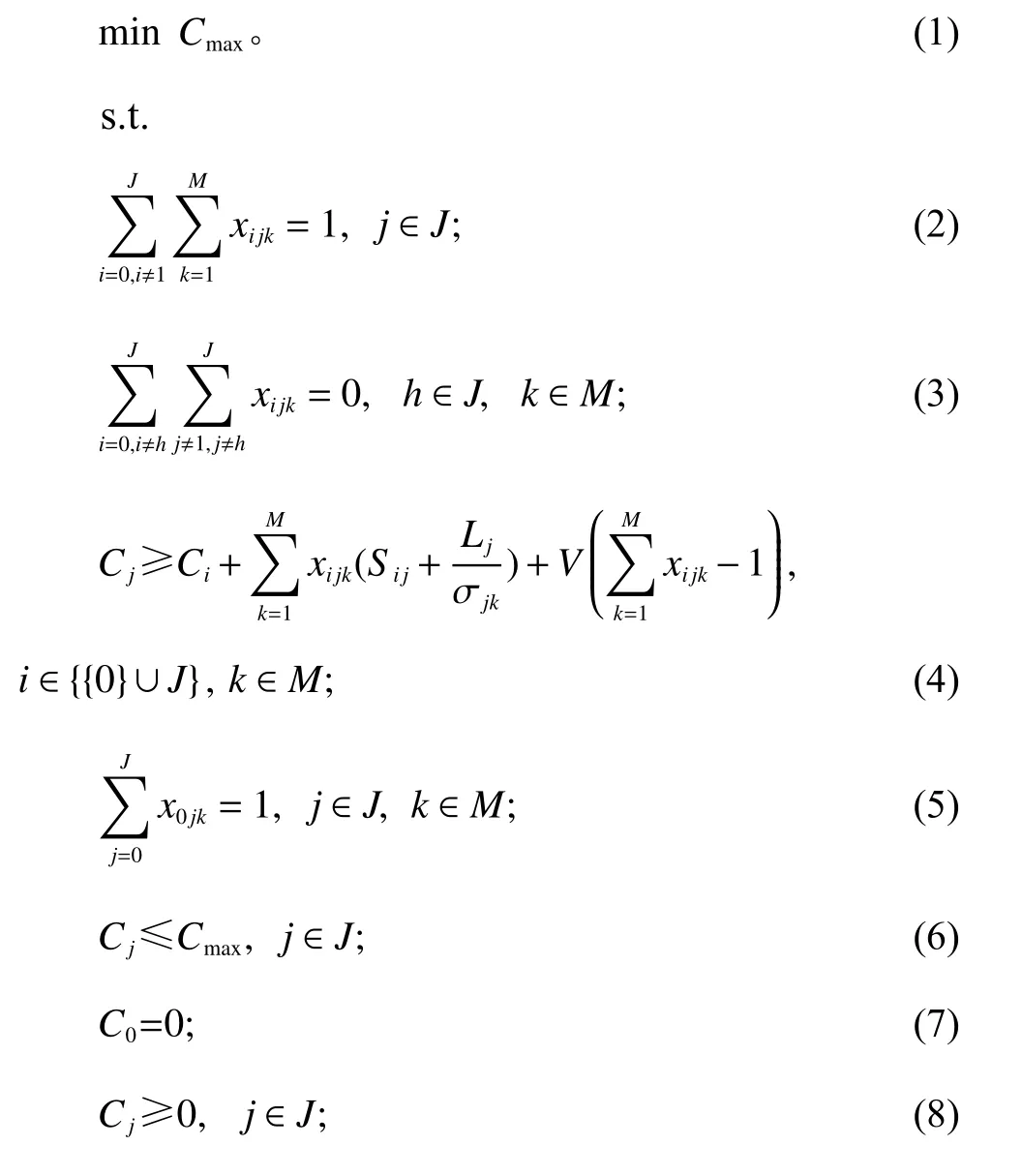
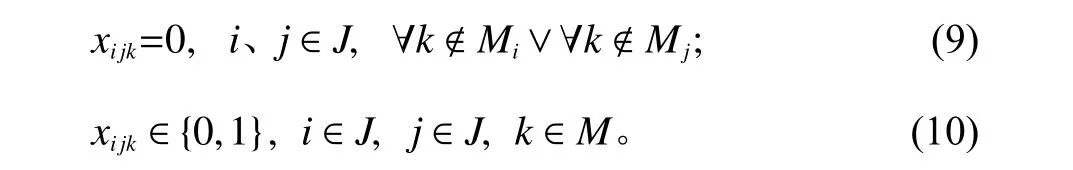
其中，式(1)为目标函数；约束(2)表示每一个工单只能被分派到一个线体上加工；约束(3)表示每一个工单只能被加工1次；约束(4)确定每一个工单的完工时间，并确保工单j不会先于本身、晚于本身完工，且紧邻工单之间存在序相关的设置时间；约束(5)表示任何线体上有且只有1个工单属于该线体第1个上机工单；约束(6)表示Cmax为所有工单的最大完工时间；约束(7)表示虚拟工单不占用线体使用时间且其完工时间为0；约束(8)表示工单j完工时间的可行域约束；约束(9)为工单加工约束，工单不允许被指派到不可加工的线体上；约束(10)为决策变量的取值约束。

2 混合遗传算法实现

本文针对UPMSP_JPCSST提出将GA算法和IG算法的破坏与构建操作相结合，从而设计兼备全局优化能力和局部优化能力的求解算法。该操作侧重于解的局部探索，可以很好地和GA算法的全局搜索相结合，并由GA算法的进化操作保留执行构建操作得到的优良染色体片段。此外，把破坏、构建机制嵌入变异操作，从而保证种群的多样性。GAIG的求解框架如图1所示。

2.1 编码设计

根据UPMSP_JPCSST的特性，可加工线体限制会使调度解空间中存在不可行解。为避开不可行解，提高求解效率，本文采用一种前后双层的整数染色体编码方式表示一个可行的调度计划，即工单排序向量(job sequence vector，JV)、线体选择向量(machine assignment vector，MV)。其中，JV层基因必须满足工单唯一性约束，MV层基因必须满足工单加工约束。以图2中5张工单、3条线体的问题为例，如果该染色体是合法的，那么表示在线体1上加工的工单序列为4；在线体2上加工的工单序列为2→5；在线体3上加工的工单序列为1→3。

2.2 带修复交叉操作

交叉算子作用于染色体的JV层。要保证交叉后的新染色体仍然可行，要求新染色体必须满足上述2个约束。

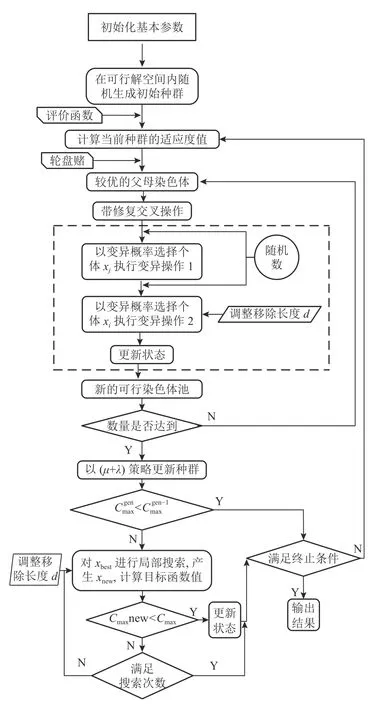
图1 GAIG求解框架Figure 1 Framework of GAIG

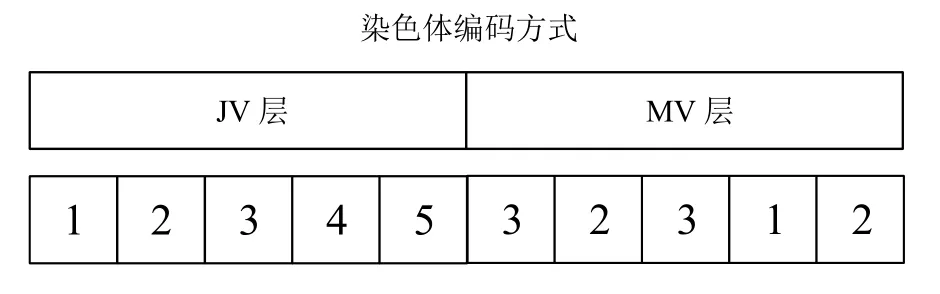
图2 染色体的编码方法Figure 2 A coding solutions of chromosome

1) 随机产生一个交叉点，交换父代染色体JV层(下面简称P)交叉点前的基因片段，以产生子代C1；2) 逐个寻找C1上的每一个基因在P2中的位置，将P2上该位置的基因替换为空值并将C1上的该基因替换为空值；3) 完成遍历后，P2中剩余的基因即子代C1的缺失基因集合W2，C1中剩余的基因即子代C1的多余基因集合W1；4) 在W1内按从左到右的顺序逐个取出多余的基因，并在C1中找到第1个对应的基因，在基因集合W2内按照从左到右的顺序取出缺失的基因填充。5) 按交叉前P1染色体首尾2层的基因映射关系，填充交叉后C1染色体MV层的基因，得到合法的新子代染色体C1；新子代染色体C2以同样的方法得到。假设交叉位置为3，交叉过程如图3所示。

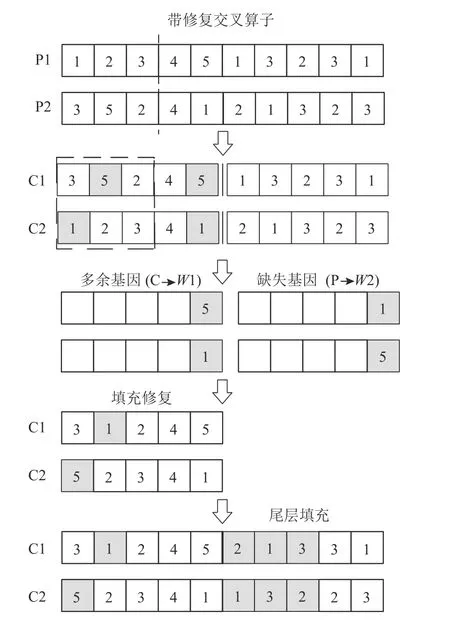
图3 交叉操作示意图Figure 3 Diagram of cross operation

2.3 变异操作

2.3.1 面向更换线体邻域结构

本邻域结构作用于染色体的MV层，该层每个基因位都有其特定值域，即变异后需满足工单加工约束。其基本思想为：历遍染色体JV层，对于JV层中被选择的基因，在其特定值域内随机产生加工线体基因，并以该线体的基因编号替换掉原有的线体基因，如图4所示。

2.3.2 基于IG算法的破坏与构建操作

图4 邻域结构示意图Figure 4 Diagram of neighborhood structure

为获得更好的优化解，结合该企业UPMSP_JPCSST和GA算法的特点，在求解算法的变异算子中嵌入一种基于IG[13]算法的破坏与构建机制。对交叉产生的新个体，以概率执行该操作(具体如图1和2.4节所示)，从而提高种群的多样性。

2.4 局部优化操作

局部优化操作分为破坏和构建2个阶段，详细步骤如下。

破坏阶段以随机方式从个体序列中移除部分序列。文献[13]通过试验得到的移除长度d并没有通用性，本文经过测试得到较适合本案例的破坏长度d。在变异操作的破坏步骤中，初始破坏长度d0=0.1n，在迭代进程中，随着种群多样性的降低而线性变长dgen=dgen−1α；在局部优化操作中，初始破坏长度随迭代进程及种群进化情况而变化，dgen=dgen−1δεiter；每代更新d值。其中，α为上升系数，α=1.01；δ为下降系数, δ=0.97；ε为种群进化停滞系数，ε=1.05；iter为种群进化停滞代数；gen为当前迭代代数；n为工单数量。

构建阶段将被移除的序列按照被移除的顺序逐个重新插回原保留序列，直到重新构成完整的合法序列。类似于NEH (the heuristic of NAWAZ, ENSCORE and HAM)[15]算法，定义工单的插入邻域为已有序列中所有可能插入的位置，即将待插入工单逐个插入保留序列上的每一个可插入位置。根据目标函数值选择最优的位置，直到合法序列重新生成。

终止条件若执行局部搜索的个体停滞进化代数达到5次，或个体得到进化，则结束算子，如图5所示。

2.5 GAIG算法步骤

在GAIG中，初始种群随机生成，选择算子采用轮盘赌[16]方法，更新策略采用(μ＋σ)策略[17]，算法以运行时间作为终止准则，运行时间根据算例的规模而定，具体如 3.2 节所示。算法步骤如图6所示。

图5 局部优化方法伪码图Figure 5 Pseudo-code of local optimization method

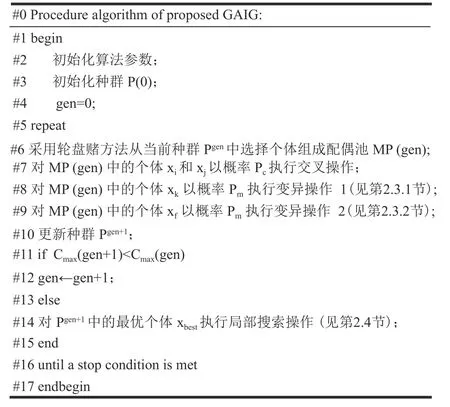
图6 GAIG算法伪码图Figure 6 Pseudo-code of the proposed GAIG

3 实验及分析

3.1 测试算例与实验环境设定

由于广东某大型合作家电企业对提供的两千多条具有代表性的实际案例数据有保密性要求，本文不便公开其数据。为了验证本文所提出的GAIG算法求解该企业车间UPMSP_JPCSST的性能，这里以该案例数据为基础，提取案例所具备的特征，引入文献[18]实验设计的思想，随机生成24组具有企业实际问题特征的测试算例，算例命名格式为n-Øδγ。其中，参数n为工单数量；参数Øj和δk共同确定线体k对工单j所用物料的单位产能，衡量加工能力的异质性。Øj衡量工单j的异质性，决定同一线体对不同的工单所用物料的单位产能；δk衡量线体k的异质性，决定不同的线体对同一个工单所用物料的单位产能。对于工单j和线体k，μj～U(Øj)，ξk～U(δk)，则线体k对工单j所用物料的单位产能σjk=μjξk；参数γ表示测试环境中所有工单将会用到的物料型号与所属产品型号的种类规模，构成了换产的异质性；参数Lj为工单j需生产的产品数量，详细参数如表2所示。线体上第1个上机工单其设置时间为300，相邻工单其产品型号相同则不需要设置时间，相邻工单其产品型号不相同但加工所需的物料型号相同，其设置时间为100，否则设置时间为300。

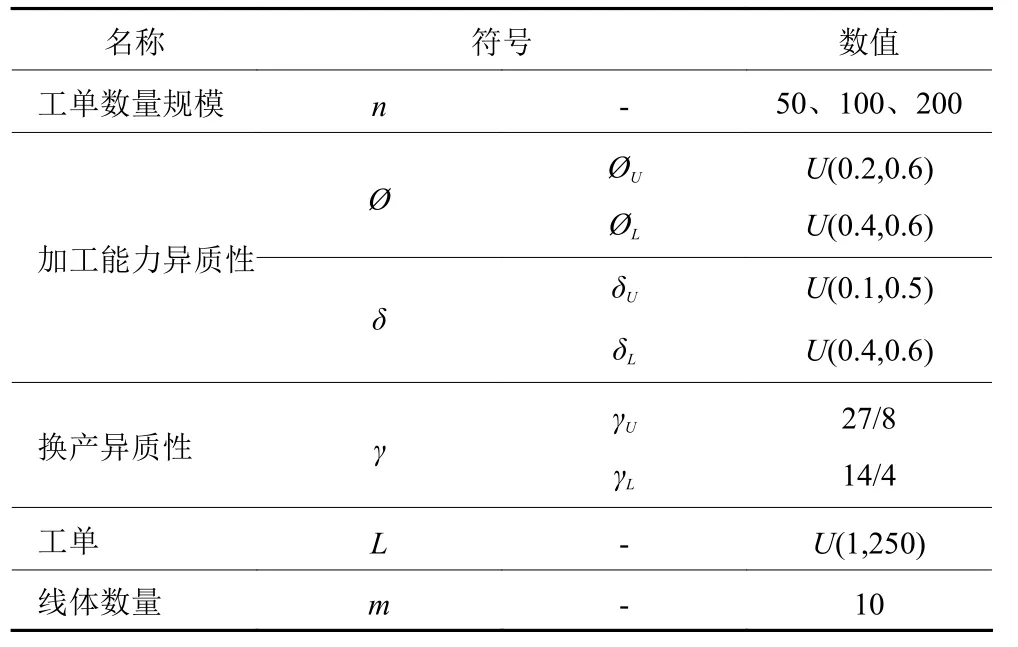
表2 测试算例参数Table 2 Parameters of experimental case

运行环境如下。计算机系统为Windows10，处理器为Intel®Core™i7-8700 @ 3.20 GHz 3.19 GHz，RAM内存为16.0 GB，算法采用Matlab R2016b编程实现。

3.2 各种算法性能比较

首先，为更好地测试GAIG算法在求解该企业车间UPMSP_JPCSST时的有效性，实验以NEH[18]算法、 IG算法、GASA算法、SA算法、GA算法和GATS算法为比较对象。7种算法在每个算例组合下分别进行10次独立实验，将得到的最大完工时间Cmax、平均流水时间Fave和换产时间占比P共1个优化指标和2个观察指标求均值，作为算法评估的依据，结果如表3所示。其中，GAIG算法参数设置如下：种群大小为100，交叉率Pc为0.8，变异率Pm为0.05，移除长度d如2.4节所述；其他算法中SA初始温度为100，冷却系数为0.95；TS的禁忌长度为100，候选解个数为100个；通用参数及邻域结构与GAIG一致。所有算法均随机初始化初始种群。此外由于混合算法与单一算法每一代的迭代时间差异性大，且基于该企业对于算法运行时间的苛刻要求，本文以运行时间作为算法的终止条件。工单规模为50的算例，运行时间为20 s；工单规模为100的算例，运行时间为40 s；工单规模为200的算例，运行时间为80 s。表3为7种算法在各个算例组合下的测试结果。测试结果中，7种算法的性能分布和对企业实际案例数据进行计算得到的性能分布相似，表明以该方法生成的随机测试数据具有一定的可用性。

由表3可知，1) 从{#1,#3,#5,#7}、{#2,#4,#6,#8}、{#9,#11,#13,#15}、{#10,#12,#14,#16}、{#17,#19,#21,#23}和{#18,#20,#22,#24}对比组可以看出，在加工能力异质性大的测试环境中，拥有更换线体邻域结构的算法如SA、GASA等具有优势，其能够从压缩工单的加工时间的角度减少平均流水时间，进而提升调度性能；而相比基于部分序列构建的IG算法，NEH这类全序列构造型的算法也能够从该角度取得更好的优化效果。

2) {#1,#2}、{#3,#4}、{#5,#6}、{#7,#8}、{#9,#10}、{#11,#12}、{#13,#14}、{#15,#16}、{#17,#18}、{#19,#20}、{#21,#22}和{#23,#24}定量对比组可以看出，无论换产异质性大还是小，NEH、IG等具有构造机制的算法均能取得相对于其他算法更小的换产时间占比；在换产异质性增大的扰动下，虽然各个算法性能指标均在一定程度上得到劣化；但是相对于其他算法，NEH和IG算法的性能指标的劣化程度相对缓和，其能够从压缩工单之间的设置时间的角度极小化最大完工时间。

3) 从{#1,#9,#17}、{#2,#10,#18}、{#3,#11, #19}、{#4,#12,#20}、{#5,#13,#21}、{#6,#14,#22}、{#7,#15,#23}和{#8,#16,#24}定量对比组可以看出，算例规模的扰动对SA的影响较大。SA随着算例规模的增大，性能急剧下降，只适合小规模算例。而具有并行搜索优势的算法如GA、GASA、GATS则随着算例规模的增大，优势逐渐显现，但受制于运行时间，优势无法完全体现。而IG、NEH算法基于不受运行时间节制的优势，随着算例规模的增大，性能指标逐渐具有优势。在加工能力异质性小的环境下，IG和NEH均会在算例规模逐步增大时偶尔出现不同程度的性能指标劣化现象，十分不稳定。

表3 7种算法实验统计结果Table 3 Test statistical results of seven algorithms

4) 在各个算例组合中，GAIG算法几乎都能得到最好的结果。首先GAIG算法具有遗传算法并行搜索、迭代进化的特点，不但具有面向加工能力方向进行优化的邻域结构，又拥有针对换产时间方向进行优化的机制，使GAIG算法能够在各种复杂的算例组合中具有普遍可用性，同时，又区别于其他混合算法对运行时间的依赖性，具有更优的调度性能。其次，以200-ØUδU-γU算例为例，图7分别给出了除确定性算法NEH以外其他6种算法在80 s内的最优Makespan收敛曲线。可以看出，GAIG算法的收敛速度明显快于除IG算法以外的其他算法，运行时间非常短且优化质量也比其他算法更高。因此，GAIG算法无论在运算时间还是运算结果上来看，都具有相对于其他算法的优越性，能够满足该企业对算法的快速反应和高质量方案的要求。最后，为了说明GAIG算法的鲁棒性，排除确定性算法NEH后，将6种算法在每个算例规模下的8个测试环境中多次运行所得数据绘制成箱线图，如图8所示。从图8的统计结果不难看出，GAIG算法对各种算例组合都保持着较高的求解鲁棒性，能够满足该企业对算法的高鲁棒性要求。

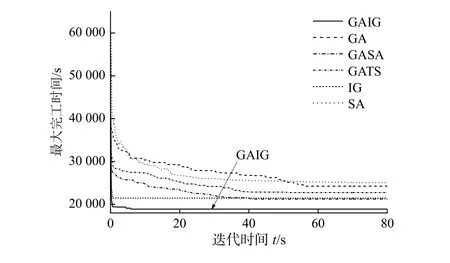
图7 收敛曲线Figure 7 Convergence curves

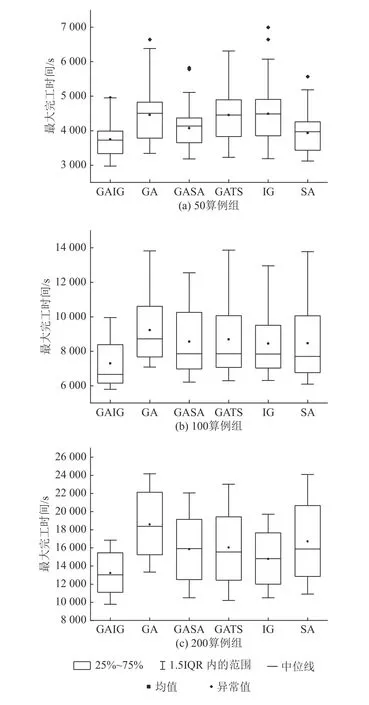
图8 6种算法在不同规模算例下的箱线图Figure 8 The boxplot of 6 algorithms in different scale case

4 结束语

本文针对家电企业总装车间需要同时考虑工单加工约束和序相关设置时间等难点，以最小化最大完工时间为目标，设计GAIG算法。该算法结合遗传算法全局搜索性能较优和IG算法局部优化性能较强且速度快的优点，通过遗传算法进行全局搜索寻得的较优解作为局部搜索算法的初始解进行深度搜索，而经过破坏与构建机制深度优化的高质量解反过来提高遗传算法种群的多样性。同时，在各种具有企业实际数据特征的测试算例中与其他算法进行比较，说明该算法的有效性、稳定性与鲁棒性，符合企业实际生产的要求。

针对本文的不足，未来将从以下2个方面做进一步的研究。1) 考虑带有交货期等更为复杂的车间环境；2) 研究极小化最大完工时间、拖期率和齐套性的多目标优化算法。